GB/T 7704-2017标准残余应力计算公式解析
2020-12-25巴发海徐凌云李思瑾
巴发海, 李 凯,徐凌云,李思瑾
(1.上海材料研究所 上海市工程材料应用与评价重点实验室,上海 200437;2.上海海关工业品与原材料检测技术中心, 上海 200135)
金属构件在生产制造及服役过程中都会产生残余应力,残余拉应力可能使铸件或焊件在冷却过程中发生开裂,而喷丸产生的残余压应力能提高工件的疲劳寿命。准确测定残余应力是避免残余应力危害、利用残余应力优点的重要基础工作。标准GB/T 7704-2017 《无损检测 X射线应力测定方法》 为国内广大测试人员提供了重要的检测依据,但是其对于原理的描述却不够详尽,尤其对于三维残余应力测试部分需要进一步细化。残余应力测试理论分散在材料力学、弹性力学以及部分数理统计等部分中,较少有文献资料集中完善地描述整个过程,这给标准GB/T 7704-2017的普及使用带来一定的困难[1-2]。笔者基于柯西应力、柯西应变、胡克定律等弹性力学知识,较为完整地推导了残余应力的测试公式,并具体分析了平面应力与三维应力状态下应力张量的计算过程,解释了一些容易误解的概念符号,指出了在测试过程中需要注意的问题。
1 任意方向正应变εφψ与应力张量σij的关系
X射线测定残余应力的基本坐标系如图1所示,以试样表面为xOy平面,垂直于试样表面方向为z轴方向建立xyz坐标系。εφψ为(φ,ψ)方向上的正应变,其中ψ为εφψ与z轴的夹角,φ为εφψ在xOy平面的投影与x轴的夹角。σφ在xOy平面内,为待测应力方向,其与z轴组成的平面为待测平面。GB/T 7704-2017在其3.2节表1中描述:“τφ是σφ作用面上垂直于试样表面方向的切应力分量”[1],可见τφ方向与z轴方向一致,这与常规表述方法有所不同。X射线法直接测定的数据是衍射角,根据布拉格方程可以计算得出以εφψ方向为法向量的平面晶面(衍射晶面)的应变,即εφψ。
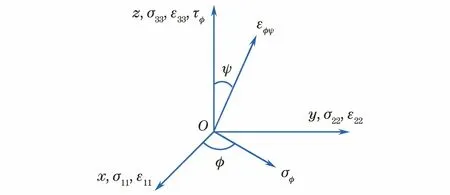
图1 X射线测定残余应力坐标系
1.1 εφψ计算
εφψ表示(φ,ψ)方向上的正应变,在小变形条件下,根据柯西应变公式可以得到εφψ与应变张量分量εij之间的关系[3],如式(1)所示。
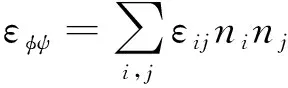
(1)


表1 ninj计算结果
通过广义胡克定律可以进一步建立εφψ与应力张量σij之间的关系[3]。在各向同性条件下如式(2)所示。

(2)

将式(2)代入式(1)得

(3)

合并同类项可得
(σ11cos2φ+σ12sin2φ+σ22sin2φ)sin2ψ+
(σ23sinφ+σ13cosφ)sin2ψ+σ33cos2ψ
(4)

cos2φsin2ψ+sin2φsin2ψ+cos2ψ=1
(5)
将式(4),(5)代入式(3)可得式(6)。
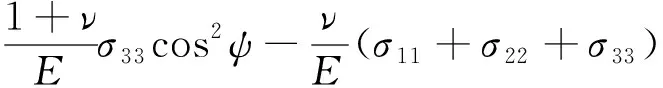
(6)
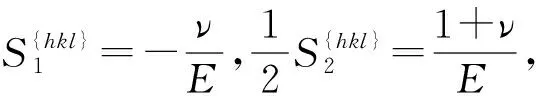

(7)

1.2 σφ及τφ的计算
在小变形条件下,根据柯西应力公式可以得出(φ,ψ)方向上总应力Tφψ、正应力分量σφψ、切应力分量Sφψ与应力张量分量σij之间的关系[3],如式(8)(10)所示。

(8)
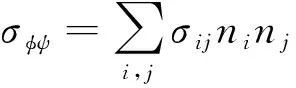
(9)
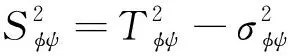
(10)
式中:i,j,k=1,2,3。
当ψ=π/2时,将{(φ,ψ)=π/2}简写为φ,σφψ即为图1中的正应力分量σφ,切应力分量Sφ在z轴上面的分量为τφ。φ对应的方向余弦为

(11)
将式(11)代入式(9)可得
σφ=σ11cos2φ+σ22sin2φ+σ12sin 2φ
(12)
令z轴单位向量为z=(0,0,1),采用向量表示
τφ=Sφ·z=(Tφ-σφ)·z
由于σφ与z垂直,σφ·z=0,因此有
τφ=Tφ·z
(13)
即τφ同时为Tφ在z轴上的分量,
化简可得:
τφ=σ13cosφ+σ23sinφ
(14)
式(12),(14)分别是GB/T 7704-2017中的公式(4)和公式(5)。将其代入式(7)可得
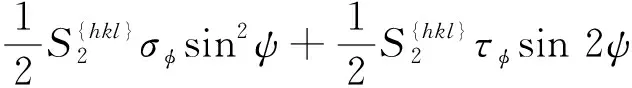
(15)

式(12)适用于三维应力状态与平面应力状态,但是部分资料中对式(12)在平面应力下的表述如式(16)所示[4]
σφ=σ11cos2φ+σ22sin2φ-τ12sin 2φ
(16)
这是由于弹性力学与材料力学中对于切应力方向规定不同,实质并无差别。平面应力莫尔圆如图2所示。

图2 平面应力莫尔圆
采用弹性力学中的应力莫尔圆计算σφ,也可以获得与式(16)一致的结果。C,E,D点分别为x轴,y轴以及σφ对应平面。莫尔圆中两应力的夹角是实际应力夹角的两倍,因此C,E在一条直线上,∠DO′C=2φ。在莫尔圆中由几何关系可知
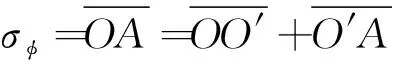
(17)
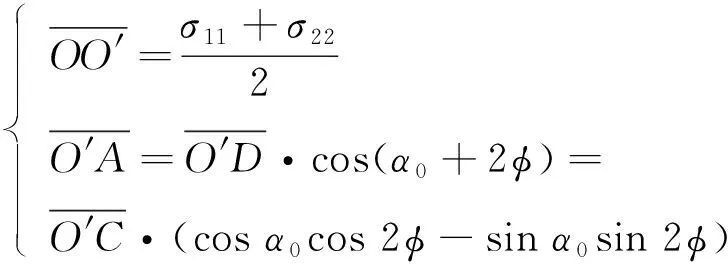
(18)

(19)
将式(19)代入式(18),然后代入式(17)可得
σφ=σ11cos2φ+σ22sin2φ-τ12sin 2φ
1.3 布拉格方程分析
当X射线到达晶面时,有一部分射线发生折射,另一部分发生反射,应力仪可以接收反射的这部分射线,当反射线光程差刚好等于波长时,反射射线会发生加强,即产生衍射。布拉格方程表明,当晶面间距d、入射角θ、波长满足2dsinθ=nλ时,会发生衍射,此时接收器会检测出一个波峰,记录此时的入射线角度,便可计算出反射线角度,即衍射角。布拉格方程建立了晶面间距与衍射角之间的关系,实现了通过测量衍射角来间接测量应变。
采用工程应变时:
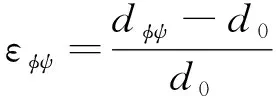
(20)
根据布拉格方程,发生衍射时可推导出
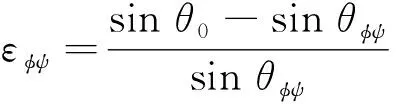
(21)
式中:d0和θ0分别为无应力情况下的晶面间距和入射角。
将f(x)=sinx在x=θφψ处二阶泰勒展开,得到
f(x)=sinθφψ+cosθφψ(x-θφψ)+o(x-θφψ)2
(22)
εφψ≈-cotθφψ(θφψ-θ0)
(23)
式中:o为泰勒展开式中的余项(佩亚诺余项)。
采用真应变时
εφψ=ln sinθ0-ln sinθφψ
(24)
将f(x)=ln sinx在x=θ0处二阶泰勒展开,得到
ln sinx=ln sinθ0+cotθ0(x-θ0)+o(x-θ0)2
(25)
εφψ≈-cotθ0(θφψ-θ0)
(26)
小变形情况下cotθφψ=cotθ0,此时无论采用工程应变或真应变,都有

(27)
2 平面应力分析
在平面应力状态下,σ33=τ13=τ23=0,τφ=τ13cosφ+τ23sinφ=0,代入式(15)可得:

(28)
将式(28)对sin2ψ求偏导,σ11+σ22+σ33为第一应力张量不变量,因此

(29)
将式(27)代入式(29)可得
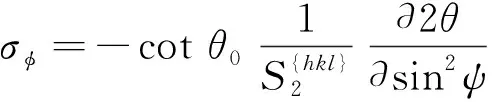
(30)

(31)
式中:α为主应力与x轴夹角;s1,s2为主应力; xy为切应力。
3 三维应力分析
在三维应力情况下,2θ-sin2ψ非直线关系,无法求得斜率。此时需要用到“±ψ角应变加减法”,即+ψ角与-ψ角对应的应变相加或相减之后再进行拟合。GB/T 7704-2017根据实际情况在两种情况下分别进行了三维应力分析。
3.1 σ33=0时的三维应力分析
对于大多数金属材料和零部件来说,常规衍射仪X射线穿透金属的深度通常在微米数量级,因此通常假设σ33=0(σ13≠0或σ23≠0或两者均不等于0)。
3.1.1σφ与τφ计算
对于给定的φ角,在一系列±ψ角进行测量,然后根据最小二乘法求可出σφ与τφ[5]。
将σ33=0代入式(15)即可得到GB/T 7704-2017中的式(7),如式(32)所示。
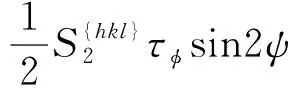
(32)
将ψ=ψ+,ψ-分别代入式(25)得

(33)
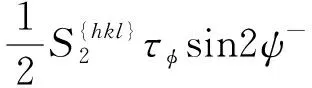
(34)
根据三角函数性质有sin2ψ+=sin2ψ-。
将式(33)与式(34)相加可得
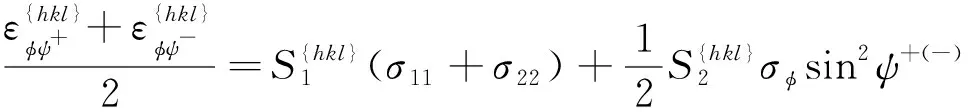
(35)
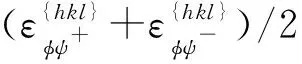
(36)
将式(33)与式(34)相减可得
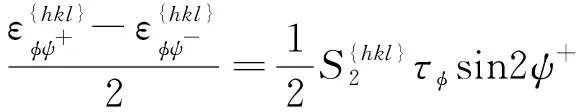
(37)
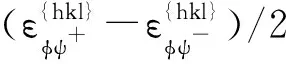
(38)
3.1.2 应力张量分析
对于复杂的应力状态,需要测定全部的应力张量分量。在张量分析中应至少测定3个独立的φ方向,在每一个独立的方向按上述方法分别测定σφi,τφi(i=1,2,3)。将σφi,τφi代入式(12)和式(14)可得线性方程组式(39),(40),即可解出各个应力张量分量。

(39)
(40)
当φ=0°,45°,90°时,代入式(30)得
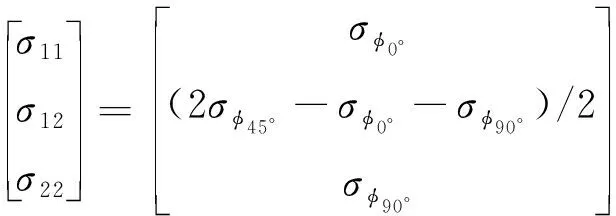
(41)
同理可得
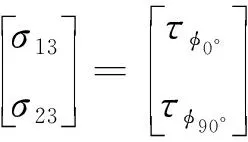
(42)
3.2 σ33≠0时的三维应力分析

(43)
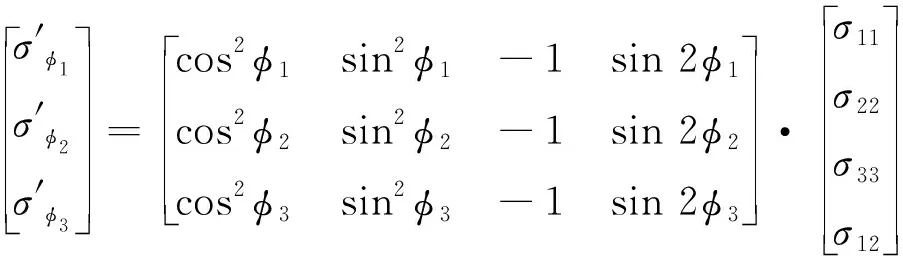
(44)
式(44)所示的线性方程组系数矩阵中前三列线性相关,因此不能通过增加φ方向来使方程组有唯一解。注意到在ψ=0°时,由式(6)可得

(45)
εψ=0°可根据式(27)计算。
联立(44),(45)可得
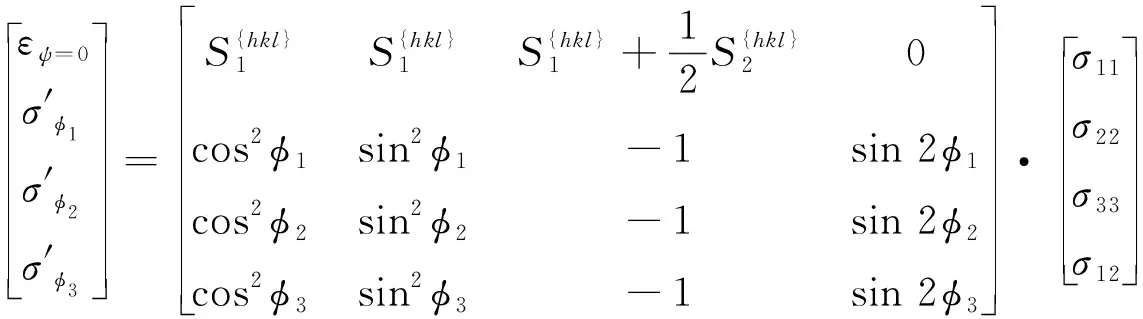
(46)
当φi=0°,45°,90°时,方程组(46)的解为

(47)

3.3 示例计算
三维应力状态正负ψ角的曲线分叉示例如图3所示[1]。下面以图3(GB/T 7704-2017中的图4)中的数据为例计算当σ33=0时的三维应力。

图3 三维应力状态正负ψ角的曲线分叉示例
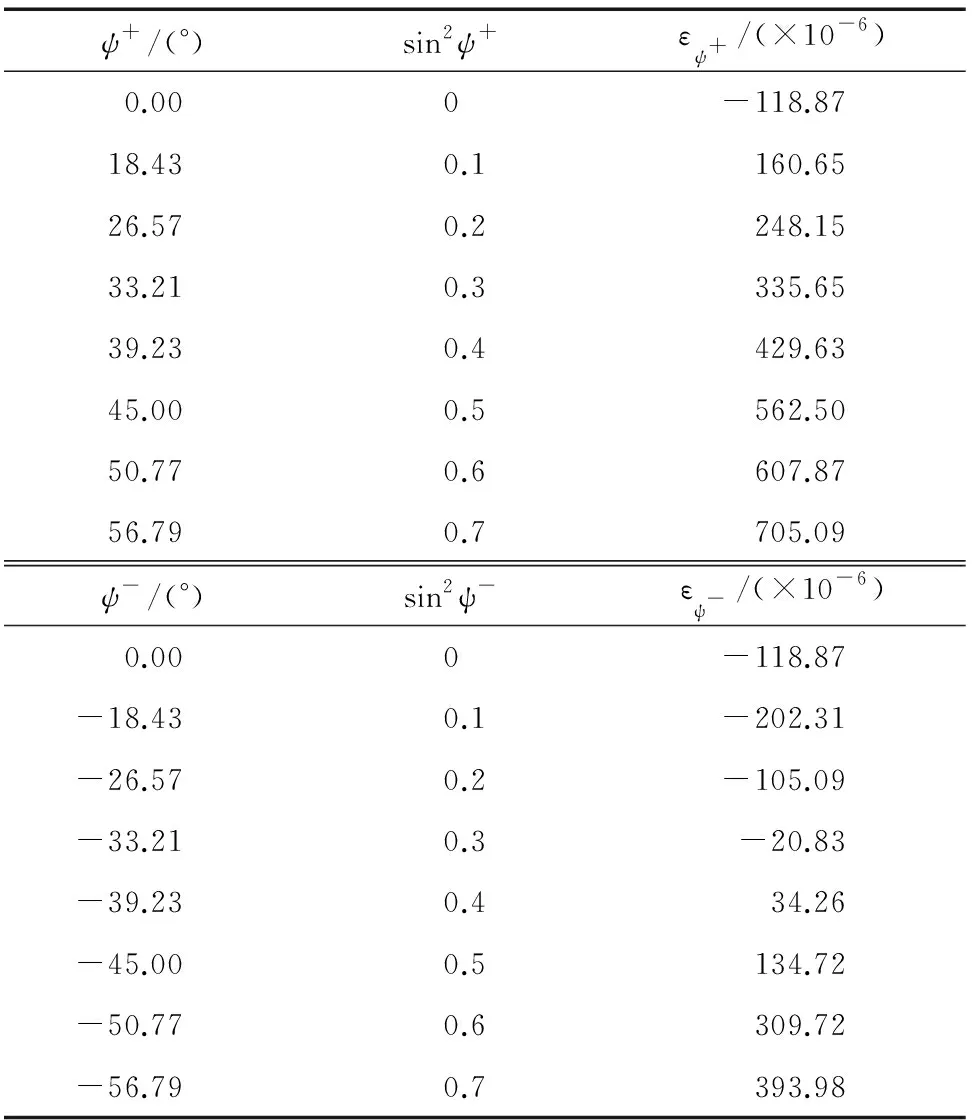
表2 ψ,ε数据
图3中的ψ、ε如表2所示,由于只有一个φ角的数据,因此这里只计算σφ与τφ。
3.3.1 σφ计算
表 计算结果
第二步:根据最小二乘法拟合为直线,结果如图4所示。

图与sin2ψ+(-)的拟合结果


(48)
3.3.2τφ计算
第二步:根据最小二乘法拟合为直线,结果如图5所示。

图与sin 2ψ+的拟合结果


表计算结果
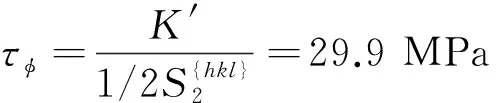
(49)

4 椭圆分析
采用±ψ角对应应变相加或相减的方法计算σφ与τφ时,τφ的误差较大。GB/T 7704-2017在4.3节“三维应力分析”中指出,在三维应力情况下,εφψ与sin2ψ的函数关系呈现椭圆曲线。对椭圆直接进行拟合,可以获得更好的结果。
4.1 椭圆拟合
令
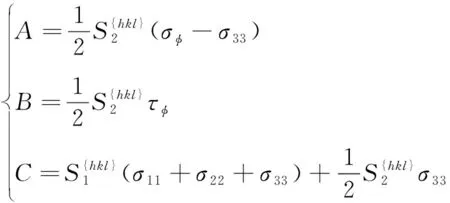
(50)
代入式(15)可得
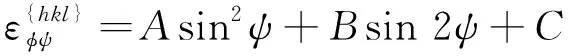
(51)
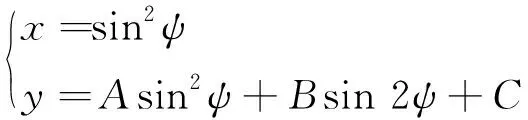
(52)
根据三角函数性质,可将式(37)对应的参数方程转换为(53)所示的一般位置椭圆的隐式方程。
(A2+4B2)x2-2Axy+y2+
(2AC-4B2)x-2Cy+C2=0
(53)
观察式(50)可以发现,当σ33=0时有:
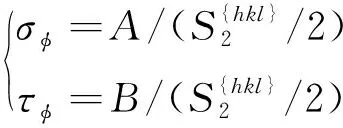
(54)
当σ33≠0时有
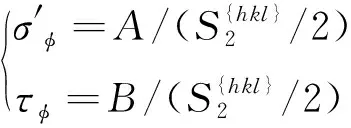
(55)
因此可以根据椭圆系数A,B来计算σφ或φ与τφ,进而代入式(39)、(40)、(46)求出各个应力张量分量。
对εφψ与sin2ψ拟合时,采用式(52)所示的参数方程更为方便。设定一函数F,根据最小二乘法定义,需要求出当F=∑(y-yi)2取最小值时的A,B,C值
F=∑(Asin2ψ+Bsin 2ψ+C-yi)2
(56)
将F分别对A、B、C求偏导得
(57)

(58)
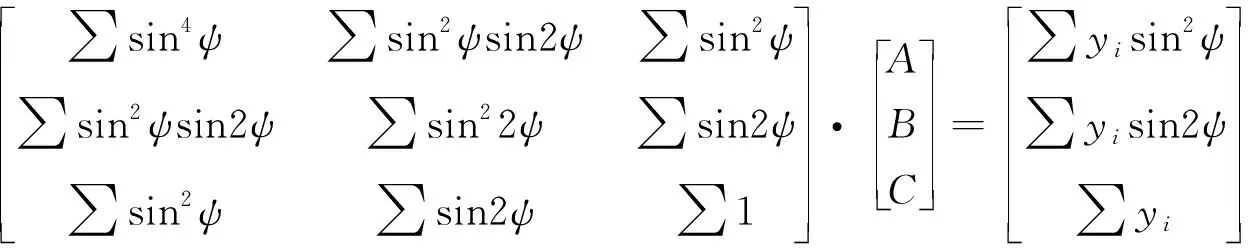
(59)
由于±ψ角成对出现,因此有
∑sin 2ψ=0, ∑sin2ψsin 2ψ=0
(60)
将(60)代入(59)可得

(61)
式中:n为ψ角数量,包括+ψ与-ψ。
求解式(59)或(61)所示的线性方程组都可得到A,B,C值。式(61)要求±ψ角成对出现,式(59)则无此要求。
4.2 椭圆拟合示例
第一步,计算方程组式(59)中的系数矩阵,结果如表5所示。

表5 方程组系数矩阵
对应线性方程组为

(62)
解式(62)得

(63)
即

(64)
可得:σφ=163.9 MPa;τφ=34.1 MPa。
拟合椭圆与原始数据如图6所示。
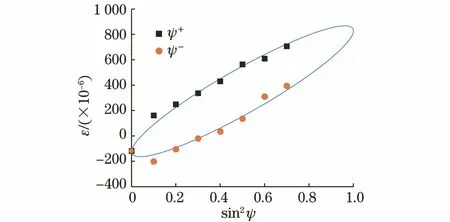
图6 式(64)对应的椭圆与原始数据
5 结语
基于X射线衍射,弹性力学以及材料力学理论对GB/T 7704-2017中残余应力的计算做了深度解析,同时对平面应力与三维应力状态下的各个正应力及切应力分量的计算难点问题做了较为详细的推演。指出理解标准中测试原理和采用相关公式时,应该注意以下几个问题。
(1) X射线法测定残余应力局限于各向同性材料的弹性变形范围内。
(2) GB/T 7704-2017中的τφ是σφ对应的切应力在z轴上的分量。
(3) 在三维应力状态下选取ψ角时,应保证sin2ψ与sin 2ψ值间隔都近似相等。
(4) 测定τφ及应力张量分量时,建议采用椭圆拟合。
