基于惯性测量的管道弯头角度与走向解算方法
2020-12-25杨理践郭方智高松巍李佳音
杨理践,郭方智,高松巍,刘 斌,李佳音,靳 鹏
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
管道广泛应用于油气产品的输送中,进行管道检测并实现管道完整性管理极其重要。管道弯头是管道埋地分布中必然存在的管道结构之一,管道弯头的曲率半径等参数又影响着管道的通过能力,是实现管道完整性管理必要的基础数据。杨金生等[1]通过计算内检测器的行进速度与通过弯头时的角速度的比值,得到曲率半径。惯性导航技术应用于管道内检测方面的研究多针对惯性导航系统中的惯性测量单元存在漂移的问题,围绕减小随距离和时间累积而增大的位置误差进行[2-3]。武汉大学以实际管线测量为例,利用里程计与非完整性约束等辅助信息抑制误差累积,并采用平滑算法进一步提高测量精度[4-5]。靳鹏等[6]利用检测器在发球筒中初始姿态可控、可测的特点,设计了迭代Kalman(卡尔曼)算法及终止迭代的判断方法,提高了初始对准及后续管道地理坐标的解算精度。
笔者利用惯性测量单元和里程计的输出信息,建立管道弯头解算模型并推导弯头角度和弯头走向,获得角度、曲率半径和走向等管道弯头参数,为管道完整性管理提供了参考依据。
1 检测原理
1.1 惯性导航测量原理
管道内检测器以输送介质的压力差为动力,在管道内部沿管道中心线运动,对管道的腐蚀、裂纹等缺陷及管道的几何变形等进行在线检测。管道漏磁内检测器结构如图1所示。

图1 管道漏磁内检测器结构示意
搭载在管道漏磁内检测器上的惯性导航系统以惯性测量单元(inertial measurement unit,IMU)为主,实时采集载体的运动姿态信息。通过将测量数据、管道外校验点和里程计数据结合,并进行解算,实现管道地理坐标的测量。
1.2 检测器坐标系统与欧拉角
惯性导航系统以一定频率采集IMU和里程计数据,并保存在存储系统中。IMU主要包含有三轴陀螺仪和三轴加速度计,用于测量检测器的角速度和加速度信息。陀螺仪和加速度计的坐标系统保持一致,y轴正方向为检测器前进方向,检测器坐标系统如图2所示。

图2 检测器坐标系统示意
ωx,ωy,ωz为陀螺仪绕x,y,z轴旋转时测得的角速度,方向垂直于转动平面,通过右手螺旋定则确定;Ax,Ay,Az为加速度计沿坐标轴测得的加速度,沿坐标轴正方向输出为正;vodo1,vodo2,vodo3为三路里程计沿检测器前进方向行进的速度。
通过引入欧拉角,描述检测器相对于地面的姿态:俯仰角θ的定义域为[-90°,+90°],上仰为正;横滚角γ的定义域为[-180°,+180°],右倾为正;航向角ψ的定义域为[0°,360°],北偏东为正。角速度,即单位时间内绕旋转轴旋转方向上的角度变化量。结合欧拉角的定义,对陀螺仪的三轴角速度ωx,ωy和ωz分别进行积分得到角位移,积分结果依次对应俯仰角θ,横滚角γ和航向角ψ。
2 管道弯头角度与走向解算方法
2.1 解算模型
管道弯头角度与走向解算主要包括数据输入、数据预处理、弯头参数解算和结果输出等4个部分。原理框图如图3所示。

图3 管道弯头角度与走向解算原理框图
其中,数据预处理包括原始数据滤波处理、补偿陀螺仪零偏误差、里程计算等。
管道弯头参数输出包含起始处里程、弯曲段中心线弧长、弯头角度、曲率半径、曲率和弯头走向等6项。
管道弯头各特征参数如图4所示。管道弯头特征为管道中心线曲率发生变化的弯曲段,其两端与直管段相连。图中,D为管道公称直径;起始处里程和管道弯曲段中心线弧长为ΔS,可由里程计数据计算得到;Δη为管道弯头角度;R为曲率半径,一般以管道公称直径D为单位。

图4 管道弯头各特征参数示意
曲率半径为
R=ΔS/(Δη)
(1)
曲率半径R的倒数即为管道曲率K
K=1/R
(2)
曲率用来表示该处管道的弯曲程度,曲率越大,管道的弯曲程度越大。
2.2 管道弯头角度解算方法
对管道弯头段的三轴陀螺仪输出角速度分别积分得到角位移后,根据角度合成算法,合成得到管道弯头角度。对陀螺仪数据进行积分得到俯仰角θ,横滚角γ和航向角ψ
(3)
式中:ωx,ωy,ωz分别为陀螺仪绕x,y,z轴旋转时测得的角速度。
搭载在检测器上的IMU通过管道弯头的过程为载体坐标系不断旋转的动态过程,任意选取该动态过程中某一时刻下载体坐标系构成的三维空间,建立三维空间角度合成模型。
(1) 三维空间角度合成模型
建立三维空间下的角度合成模型(见图5)。

图5 三维空间角度合成模型
图中,空间直角坐标系为O-xyz,P为x-O-y平面中非x轴上的一点,线段OP长为a;过P点向x轴做垂线,垂足为F,线段OF长为b,∠POF为α;过点P做x-O-y平面的垂线段HP使∠POH为β,线段OH长为c;∠HOF为ζ。
在直角三角形OPF、OHP中,存在关系:
cosα=b/a
(4)
cosβ=a/c
(5)
经数学推导可知,在直角三角形OHF中,存在
cosξ=b/c
(6)
结合式(4),(5),(6),可得
cosξ=(b/a)(a/c)=cosαcosβ
(7)
ξ=arccos(cosαcosβ)
(8)
式(7),(8)完成了在三维空间下对两个垂直平面x-O-y和P-O-H中角度分量α和β的合成。
(2) 管道弯头角度合成算法
将检测器通过管道弯头时的姿态变化分解成3个部分,分别为绕x轴旋转θ,绕y轴旋转γ和绕z轴旋转ψ。结合管道检测的特点分析,检测器在管道中运动时受到约束,即其在沿管道中心线单向前进时,绕前进轴(y轴)旋转得到的横滚角γ对于管道弯头角度的大小没有贡献。所以在计算合成管道弯头角度时,只考虑绕非前进轴(x轴和z轴)旋转得到的俯仰角θ和航向角ψ。管道弯头角度合成如图6所示。
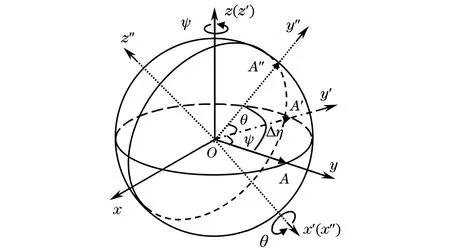
图6 管道弯头角度合成示意
图6中,坐标系O-xyz依次经过绕z轴旋转ψ、绕X轴旋转θ后得到O-x′y′z′和O-x″y″z″,A′和A″由x-O-y平面内的一点A依次经两次旋转得到。
由于陀螺仪三轴相互正交,式(7),(8)适用于检测器通过管道弯头时整个动态过程的角度合成,可推得
cos Δη=cosθcosψ
(9)
Δη=arccos(cosθcosψ)
(10)
式中:Δη即为计算得到的管道弯头角度,结合里程计数据可计算该段的曲率半径和曲率。
2.3 管道弯头走向解算方法
结合检测器沿管道中心线单向前进的运动特性,得到描述弯头走向的八种结果,为正左、正右、正上、正下、左上、左下、右上和右下。载体纵轴(y轴)指向大地平面的上方为上,反之为下;载体纵轴(y轴)在大地平面上的投影指向弯头起始处管道中心线的左侧为左,反之为右。从弯头起始处沿管道中心线看去,弯头走向如图7所示。
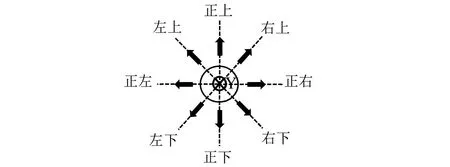
图7 管道弯头走向示意
利用IMU的三轴加速度计数据,可计算重力加速度g并解算检测器在管道弯头起始处的姿态。
(1) 弯头起始处姿态信息
由于弯头起始处的航向角ψ0仅作为航向基准,可任意给定,所以只需要计算弯头起始处的横滚角γ0和俯仰角θ0以提供弯头走向解算的初始姿态信息。
检测器姿态解算模型如图8所示。载体坐标系为O-xyz,重力加速度g被沿x,y,z轴分解,重力大小分别为Ax,Ay和Az。
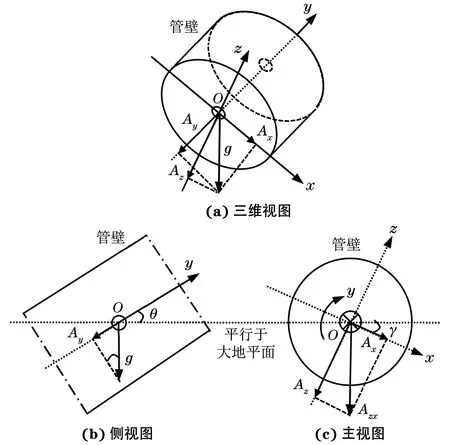
图8 检测器姿态解算模型
重力加速度大小g与三轴分量存在关系

(11)
沿平行于大地平面且垂直于检测器的方向看去[见图8(b)],在重力加速度g与y轴构成的平面下,俯仰角θ与重力分量间存在关系:

(12)
沿检测器行进方向,即从y轴正方向看去[见图8(c)]。在x-O-z平面下,横滚角γ与重力分量间存在关系
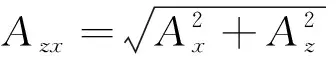
(13)

(14)
检测器在实际行进过程中,因输送介质的持续推动,难以获取检测器位于弯头起始处静止状态下的加速度计数据。由于进入弯头前检测器位于直管段且管线走向保持不变,可选取直管段各轴加速度计数据完成弯头起始处姿态信息的解算。
(2) 弯头终止处姿态信息与弯头走向


(15)

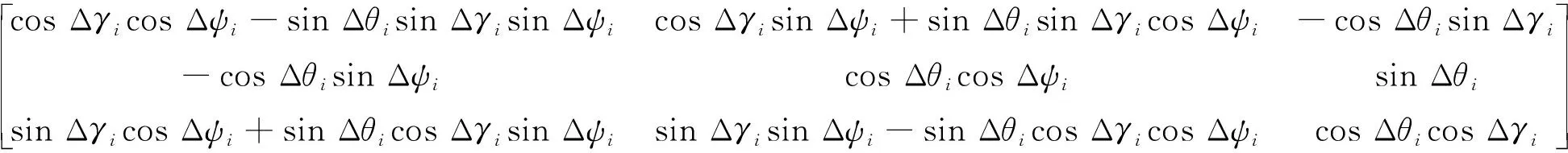
(16)
将式(16)写成T矩阵的形式

(17)
由式(16),(17)可得

(18)
经过n次计算完成整个管道弯头段姿态的更新,将整个过程表示为经过1次姿态更新得到

(19)
终止处的俯仰角θ、横滚角γ、航向角ψ可由式(17)对应的T矩阵计算得到。
由此得到了检测器在弯头起始处和终止处姿态信息的解算方法,通过计算弯头终止处相对起始处检测器的姿态偏转,实现管道弯头走向的提取。
3 试验与结果分析
3.1 试验平台
搭载有MPU6500姿态传感器的检测器完成各项调试后,从试验管道入口进入,试验过程中关闭盲板并确保管道气密性良好。打开注水加压阀加压,皮碗前后介质的压力差推动检测器沿管道中心线行进,直至检测器通过整条试验管道并到达出口。试验管道公称直径为168 mm,全段包含6个标准45°弯头,管道总长约为15.6 m。管道试验模型与试验平台结构如图9,10所示。

图9 管道试验模型示意
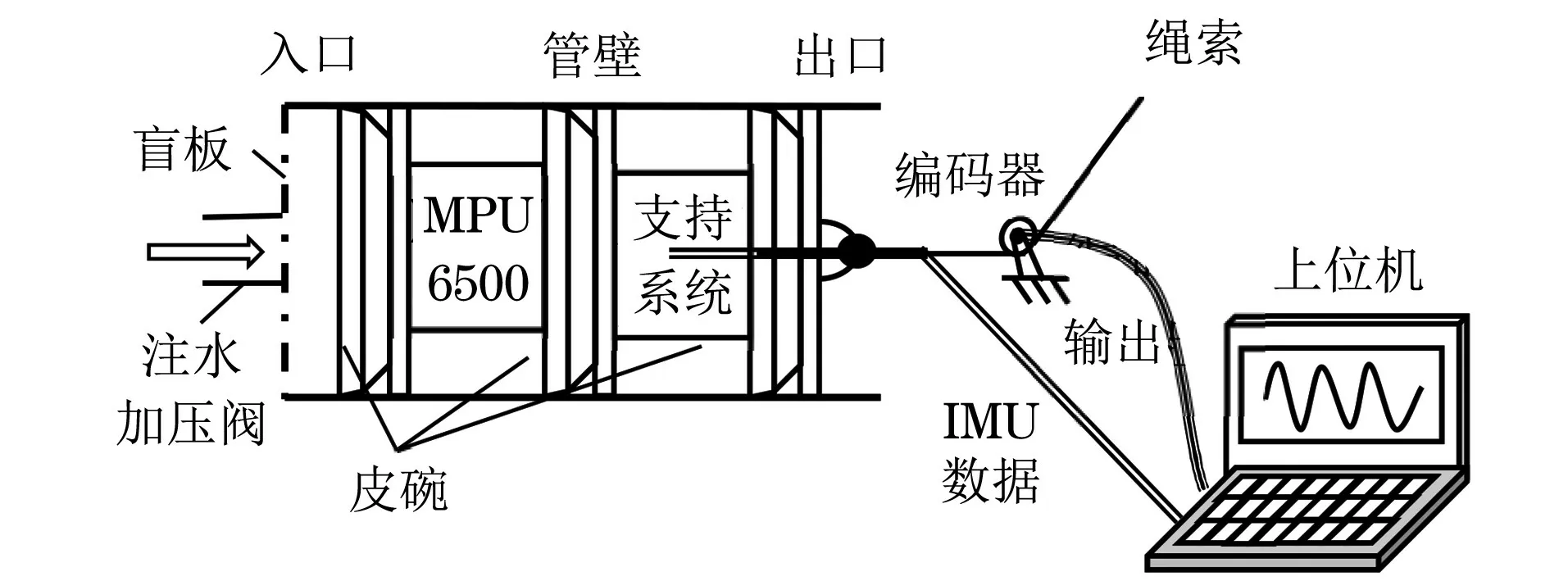
图10 试验平台结构示意
MPU6500姿态传感器实时测量检测器的运动姿态信息,经支持系统采集后与提供里程信息的编码器输出信息一同被上位机记录。
3.2 数据处理
对试验得到的测量数据进行预处理,数据预处理前后加速度计和陀螺仪的测量数据如图11所示。
由图11(a)可知,在预处理前的测量数据中,加速度计和陀螺仪数据均存在异常跳变的现象,需根据其特点对测量数据进行滤波处理;三轴陀螺仪数据的基准角速度非零,因此存在因陀螺仪失调带来零偏误差的情况,需对测量数据整体进行误差补偿。

图11 预处理前后的测量数据对比
由图11(b)可知,在预处理后的测量数据中,加速度计和陀螺仪数据均无异常跳变的现象,且三轴陀螺仪数据基准角速度均为0,零偏误差已得到补偿。
3.3 试验结果与误差分析
利用MATLAB软件解算管道弯头参数,管道弯头参数解算结果如表1所示。
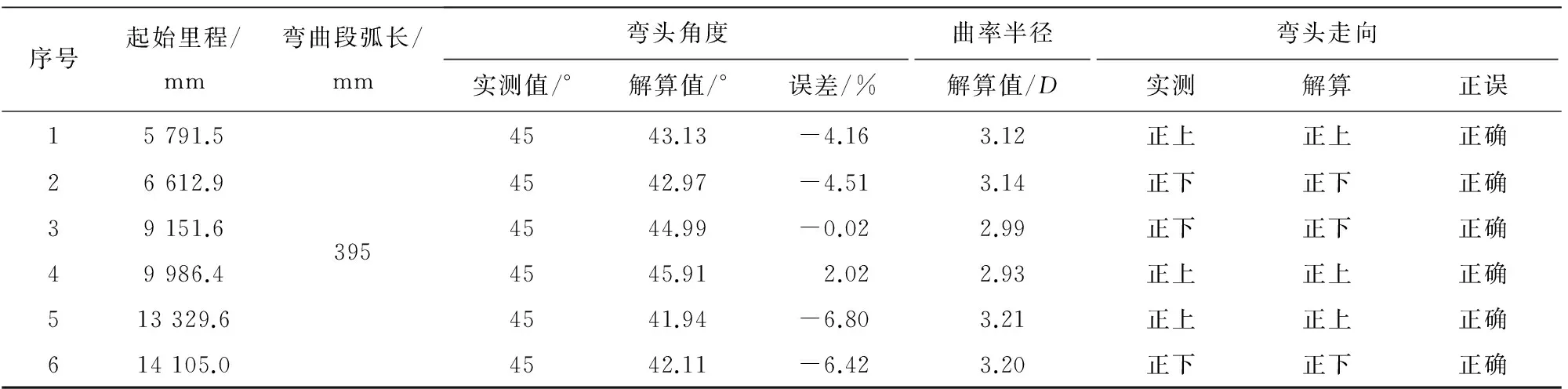
表1 管道弯头参数解算结果
表中依次给出了6个管道弯头经解算得到的参数信息。试验与解算结果表明,该方法可准确解算管道弯头走向并计算相关参数,角度计算误差在7%以内。
4 结语
利用IMU及里程计的输出信息建立了管道弯头参数解算模型,经解算可得到弯头角度、曲率半径、曲率和弯头走向等参数。该方法能够满足工程实践需求,具有较高的工程实用价值。
