不确定性输送用混联机器人滑模控制研究
2020-12-25张松云高国琴
张松云,高国琴
(江苏大学 电气信息工程学院,江苏 镇江 212013)
0 引 言
混联机器人合理结合并、串联机构,兼具并联机构柔性化水平高、承载能力强以及串联机构运动灵活、工作空间大的优点[1]。针对现有汽车涂装输送设备因采用悬臂梁串联结构而存在承载能力低及柔性化水平不高的问题,本课题自行研制了一种输送用混联机器人[2]。在运行过程中,输送用混联机器人控制系统存在如建模误差、摩擦力和外界干扰等诸多的不确定性,严重影响系统的控制性能[3]。
滑模控制动态性能好、响应速度快,可以在一定程度上解决混联机器人控制系统中存在的不确定性问题。但由于实际系统中不确定性上界信息难以获取,滑模控制需保守选取大切换增益以确保混联机器人系统对不确定性的鲁棒性[4],此时控制律的不连续会给控制系统带来严重的抖振问题,致使机械部件疲劳,严重时甚至能在短时间内破坏系统[5-6]。相对于其他高阶滑模,超螺旋滑模控制[7]具有一定的抑制抖振作用且所需信息量少,但超螺旋滑模控制律中仍存在不连续项[8-9]。为此,可通过设计其切换增益自适应律,以削弱增益选取的保守性,从而进一步抑制抖振[10]。
现常用的滑模控制自适应律是根据滑模变量大小调整切换增益进行设计的[3-4,11],但由于该种自适应设计方法无法实时较准确地应对控制系统中不确定性上界的变化,故仍可能存在切换增益过高选取的问题。文献[12]针对二维简单非线性系统提出了另一种自适应律设计方法,该方法基于包含不确定项的超螺旋滑模,通过结合等效控制原理估计不确定项值,并根据该估计值设计自适应律,以获取尽可能小的切换增益。但该自适应律未能实现滑模切换增益调整速度的自适应,在不确定性变化速度较快时,切换增益无法快速调整至最小。为此,针对不确定性输送用混联机器人,基于建立的动力学模型,将控制系统中的不确定性引入超螺旋滑模控制律中,并基于文献[12]的自适应设计方法,实时获取控制系统中的不确定性的上界信息,构建一种双重自适应超螺旋滑模,以在时变不确定性上界信息未知条件下快速获取尽可能小的切换增益,从而最大限度地抑制滑模控制抖振,提高混联机器人系统的鲁棒性能。此外,考虑到滑模控制趋近阶段滑模变量远离滑模面,该文结合全局滑模[13]改进滑模面,以解决滑模控制趋近阶段不满足等效控制条件的问题,确保双重自适应超螺旋滑模控制方法的实施并最终实现混联机器人的高性能控制[14]。最后,理论证明所提方法的稳定性并基于MATLAB仿真实验分析,验证该算法的有效性和优越性。
1 动力学建模
本课题组研制的汽车电泳涂装输送用混联机器人结构如图1所示。该输送用混联机器人是一个中间以连接杆连接的双边对称结构,主要由升降翻转机构和行走机构两个相互独立的部分组成,分别实现机器人的升降翻转及进退功能。其中,作为机器人的主体部分,升降翻转机构的控制要求较高,故该文主要研究该不确定性输送用混联机器人升降翻转机构的控制问题。选取连接杆中点位姿参数q=(z,β)T作为广义坐标,其中,z为连接杆中点在Z轴方向上的位移,β为连接杆中点绕Y轴逆时针旋转的角度。采用拉格朗日法建立输送用混联机器人的标准动力学模型[5]为:
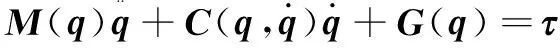
(1)
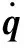
考虑系统中存在的不确定性,则不确定性输送用混联机器人动力学模型可表示为:
(2)
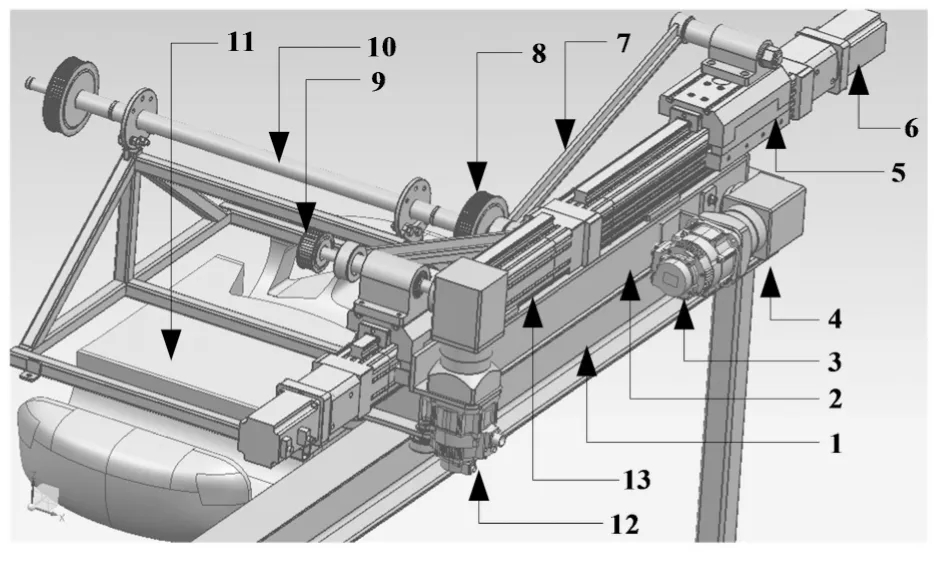
1.导轨 2.底座 3.行走驱动电机 4.减速机 5.移动滑块 6.升降驱动电机 7.连杆 8.从动轮 9.主动轮 10.连接杆11.车体12.翻转驱动电机 13.电动丝杠
2 控制器设计
2.1 滑模控制
结合全局滑模定义滑模面为:
s=w(t)-e-λtw(0)
(3)

由式(2)不确定性输送用混联机器人动力学模型可得:
(4)
对式(3)s求导,并将式(4)代入可得:
(5)
超螺旋滑模控制律定义为:
(6)

则由式(5)、(6)可得不确定性输送用混联机器人滑模控制律为:
(7)
注1:式(7)所示的滑模控制律存在未知项τd,无法应用于控制器。为解决该问题,该文基于该滑模控制律研究其切换增益自适应律。

2.2 自适应律设计
首先将输送用混联机器人控制系统中的不确定性引入超螺旋滑模控制律中。由标准动力学模型式(1)、滑模面式(3)以及超螺旋滑模控制律式(6)可得基于标准动力学模型的滑模控制律,将其代入式(5)中,可得:
(8)
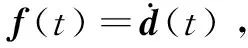
(9)

(10)
注2:切换增益α(t)、η(t)与L(t)满足:
(11)
η(t)=L(t)η0
(12)
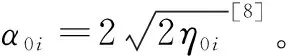
接着,该文结合等效控制原理设计自适应律。
由式(9)可得:
η(t)sgn(s)|eq=f(t)
(13)
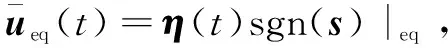
(14)
式中,τ为滤波器时间常数,其值越小,不确定项的等效值估计越准确。
定义变量δ(t)=diag[δ1(t),δ2(t)]为:
(15)
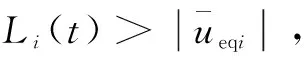
针对时变增益L(t)设计自适应律为:
L(t)=l0+l(t)
(16)
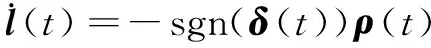
(17)
ρ(t)=r0+r(t)
(18)
(19)
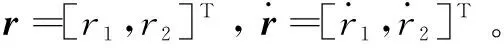
注4:在自适应律中,式(16)根据δ(t)符号即切换项与不确定项间的大小,调整切换增益的变化方向,确保了不确定性输送用混联机器人控制系统的鲁棒性;式(18)根据δ(t)大小即切换项与不确定项间的误差大小,调整切换增益变化速度,实现了切换增益的快速自适应以抑制滑模控制抖振。
综上,所设计不确定性输送用混联机器人滑模控制系统框图如图2所示。图中,qd为末端期望位姿;x=[x1,x2,…,x6]T为主动关节实际位置;q为x经运动学正解转换得到的混联机器人末端实际位姿;e为混联机器人末端位姿跟踪误差;s为滑模变量;u为控制器输出;τ=[τ1,τ2,…,τn]T为混联机器人主动关节控制输入;α和η为切换增益。
2.3 稳定性分析
假设1:不确定项f(t)满足约束条件:
|fi(t)|≤a0i<+∞,i=1,2
(20)
(21)
式中,a0=[a01,a02]T,a1=[a11,a12]T未知。
定理:针对不确定性输送用混联机器人控制系统,设计滑模控制算法如式(10)所示,自适应律如式(16)~(19)所示,则系统有限时间收敛。

图2 不确定性输送用混联机器人滑模控制系统框图
证明:首先对式(9)所示的超螺旋滑模进行稳定性分析。
引入新的状态变量:
(22)
并将其代入式(9),则超螺旋滑模可改写为:
(23)
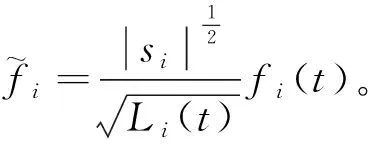
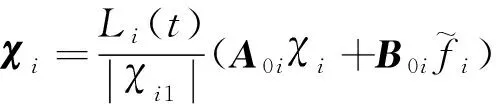
(24)

下证所设计自适应律可以在有限时间内确保Li(t)>|fi(t)|成立。
定义新变量φ(t)=[φ1(t),φ2(t)]T为:
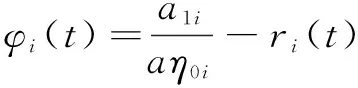
(25)
并将式(15)改写为:

(26)
定义Lyapunov函数为:
(27)
对式(27)求导,并根据式(15)~(19)可知:
(28)
(29)
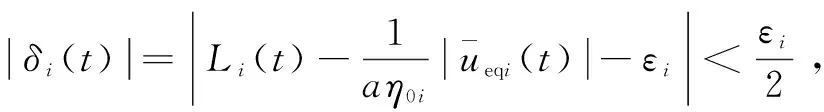
根据上述证明可知系统有限时间收敛。证毕。
3 仿真实验结果分析
为验证所提算法的有效性和优越性,基于MATLAB仿真,将所提不确定性输送用混联机器人滑模控制算法(NASTW)与未采用全局滑模面的自适应超螺旋滑模(STW)和基于滑模变量的自适应超螺旋滑模(SMASTW)作对比。将连接杆中点的广义驱动力或驱动力矩转换为关节驱动力或驱动力矩,以便实现对不确定性输送用混联机器人的实际控制。基于此,首先通过解析法求得升降翻转机构运动学逆解,并将运动学逆解方程两端对时间求导,以求得的雅可比矩阵J。通过式(30)实现广义驱动力或驱动力矩到关节驱动力或驱动力矩的转换。
τ=JTU
(30)
式中,U为关节驱动力或驱动力矩。
根据样机参数和工艺要求,确定混联机器人末端即连接杆中点的期望运动轨迹:
z=

β=
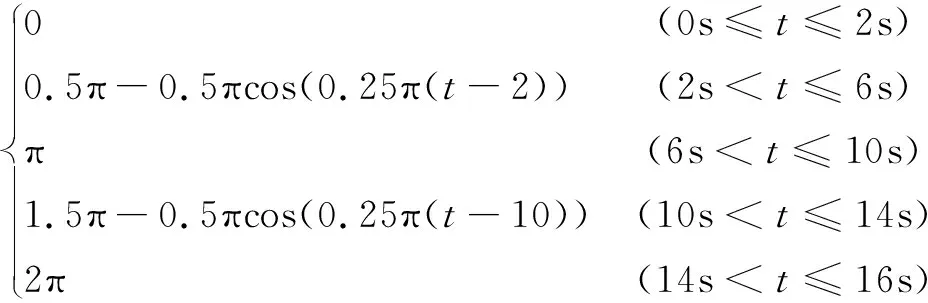
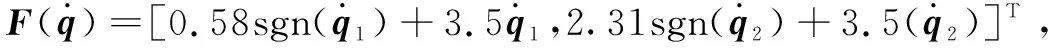

(a)z方向跟踪误差 (b)β角度跟踪误差
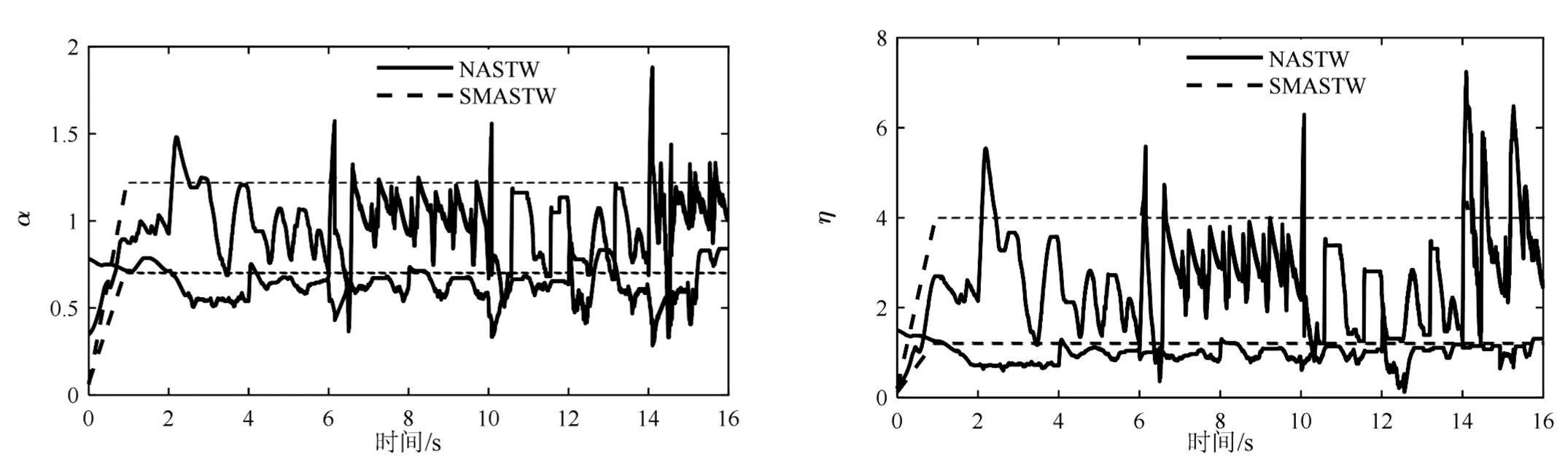
(a)切换增益α (b)切换增益η
注5:输送用混联机器人是一个双边对称结构,两边对应关节运动一致,故仅给出升降翻转机构单边主动关节控制输入变化曲线。

由图3~图5分析可知:(1)SMASTW和NASTW均具有较好的轨迹跟踪精度,且该文所提算法跟踪精度优于SMASTW,其中,连接杆中点位姿跟踪均方误差分别为7.36×10-5和2.65×10-5;(2)在不确定项大于切换项时,NASTW控制中的切换项可以自适应不确定项,且NASTW中的滑模控制切换增益普遍小于SMASTW的切换增益;(3)与SMASTW相比,所提出GNASTW系统中单边升降翻转机构三个主动关节的控制输入最大抖振幅度很小,分别降低了97.7%,97.7%和98.1%。这是由于所设计的NASTW中的自适应律能根据切换项与实时估计的不确定项间的大小及其差值实时调整切换增益的调整方向和速度,在确保混联机器人控制系统鲁棒性的同时,实现了滑模控制低切换增益的快速自适应,因此,NASTW系统具有较好的鲁棒性能。
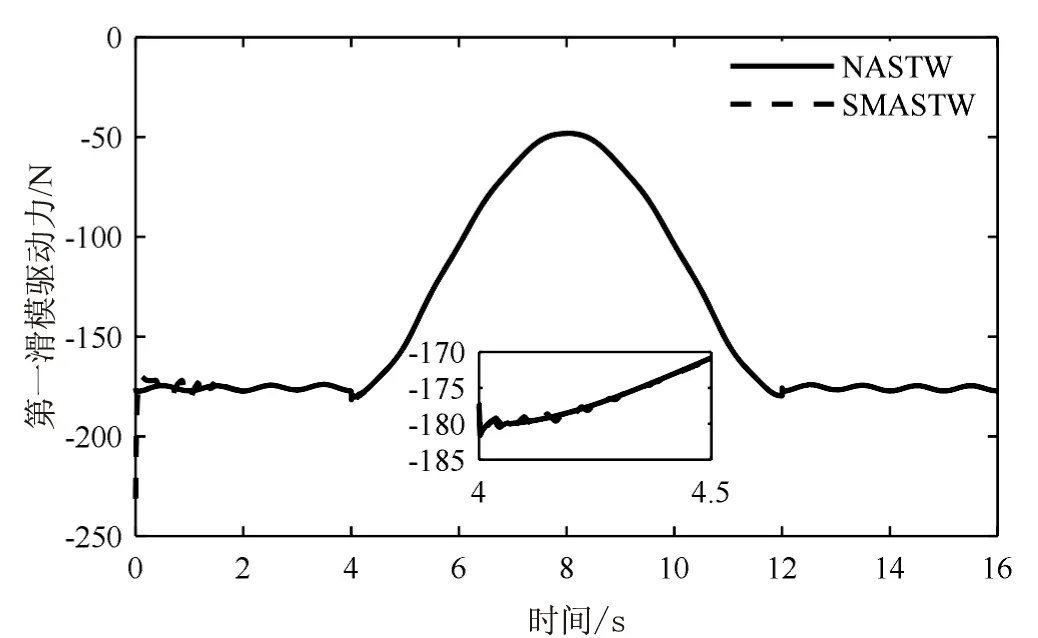
(a)第一滑块驱动力

(b)第二滑块驱动力
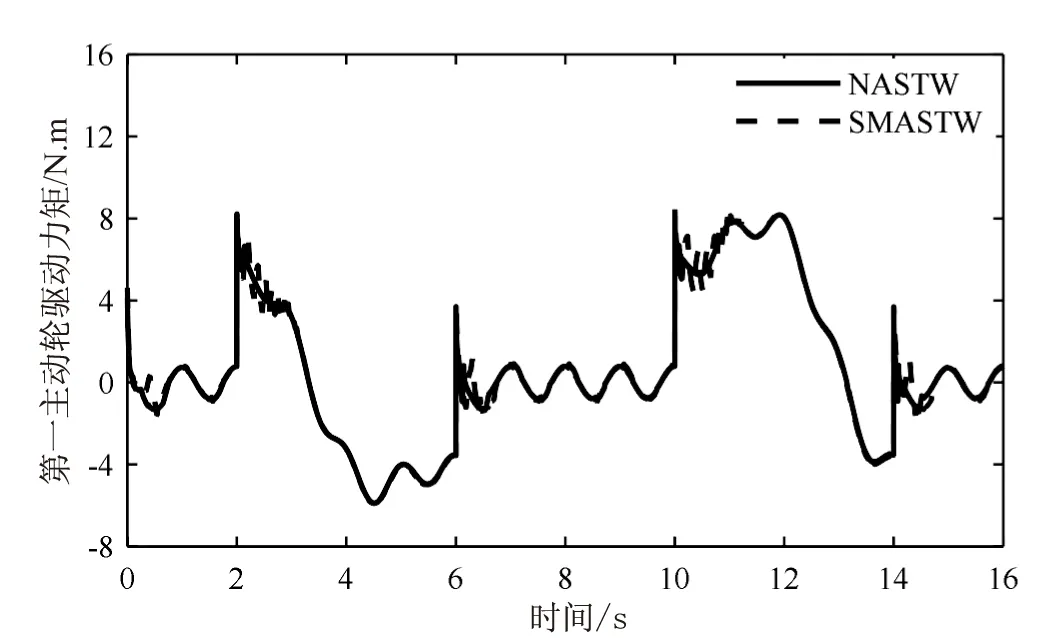
(c)第一主动关节驱动力矩
综上,该文提出的不确定性输送用混联机器人滑模控制方法具有较好的鲁棒性能,在确保系统全局鲁棒性、提高轨迹跟踪性能的同时,可大幅度减小滑模控制抖振。
4 结束语
针对不确定性输送用混联机器人提出一种滑模控制方法以实现其高性能控制,主要贡献为:
(1)将全局滑模与超螺旋滑模控制相结合设计滑模面,消除滑模控制趋近阶段,解决了趋近阶段不满足等效控制条件的问题,同时,确保了控制系统的全局鲁棒性;
(2)结合不确定性输送用混联机器人动力学模型和超螺旋滑模以获得包含不确定性的超螺旋滑模控制律,并基于等效控制原理设计超螺旋滑模切换增益双重自适应律,构建自适应超螺旋滑模控制器,最大限度地减小因滑模控制切换增益保守选取而带来的抖振问题;
(3)基于MATLAB仿真,将所提出的滑模控制算法与未采用全局滑模面的自适应超螺旋滑模控制、基于滑模变量的自适应超螺旋滑模控制相比,仿真结果证明了所提出控制方法的有效性。
