需求可拆分电动汽车车辆路径问题及其改进分支定价算法研究

揭婉晨 侍 颖 杨 珺 杨 超

(1. 浙江财经大学信息管理与人工智能学院；2. 广东财经大学国际商学院；3. 华中科技大学管理学院)

1 研究背景

由于政府的大力支持、人民社会环境意识的提高和部分城市道路燃油车限行政策的影响，越来越多的企业相继开始使用电动汽车来进行物流配送[1]。例如，德国邮政国际快递于2016年5月宣布，集团开始批量生产StreetScooter电动车用于替换现有的3万辆传统汽车。UPS于2016年与比亚迪合作，欲逐步将其车队升级为电动汽车。同时，中国邮政、顺丰快递等物流行业领跑者也先后购入电动汽车进行物流配送。然而，电动汽车含有电量约束，它需要在站点进行充电或者换电以延长其行驶里程。根据发改委发布的相关文件，我国到2020年的充换电设备需要满足500万辆电动汽车的需要[2]。电动汽车换电的操作时间小于10分钟，大大小于充电时间，并且被换下来的低电量电池可以在晚上低谷电价时批量充电，节约了充电成本，因此，换电是延长电动汽车行驶里程的重要方案。此外，在现实生活的多数场景中，客户的货物需求量往往较大，而电动汽车的载重量相对较小，经常会出现客户需求量大于车辆最大载重的情况。由此，客户需求允许被拆分，能被多辆车分别配送，充分利用电动汽车的装载能力，探讨需求可以被拆分运输的电动汽车VRP显得十分必要。

在现有的理论研究成果中，暂未发现同时考虑电动汽车配送和客户需求可拆分相关的研究，但有单独考虑电动汽车车辆路径问题(electric vehicle routing problem，EVRP)和需求可以被拆分运送的车辆路径问题(split delivery VRP，SDVRP)的研究。基于客户需求不可拆分的假设条件，许多学者研究了EVRP的相关问题，并对其作了综述，包括车队构成与规模、车辆路径和最优路径3个部分[3]。YANG等[4]提出了电动汽车换电站选址路径问题，研究在电池续航里程约束下，同时规划换电站位置和电动汽车的行驶方案。SCHIFFER等[5]在充电站选址路径问题中，考虑了电动汽车可以选择部分充电或全部充电，以及时间窗约束，模型的目标函数不仅最小化行驶距离，还最小化电动汽车的数量和充电站的数量。LIAO等[6]研究了电动汽车游览问题，该问题的目标是在给定的公路网中找到出行时间最短的路线。在现有电动汽车路径相关的研究中，大都采用启发式算法求解。HOF等[7]采用扩展自适应变邻域算法求解换电站选址路径问题；SCHIFFER等[8]提出基于动态规划的自适应大邻域搜索算法，求解换电站的选址路径问题。在精确算法方面，DESAULNIERS等[9]提出分支定价切割算法，得到含时间窗的电动汽车车辆路径问题的4种变式问题的最优解；揭婉晨等[10]通过分支定价方法，研究了在时间窗约束下的EVRP。

在SDVRP方面，DROR等[11]首先提出了SDVRP，它是传统VRP的一种扩展，允许客户需求被拆分配送，充分利用了车辆的剩余载重，大大提高了车辆的利用率，更加符合现如今的物流态势。在该问题的求解算法上，最早采用精确算法的主要有ARCHETTI等[12]及DROR等[13]。其中，DROR等[13]首先提出了SDVRP的一种弧流公式，并给出了一类新的有效不等式进行求解。接着，更多精确算法被提出用来求解SDVRP，主要有截平面法[14]、最短路径法[15]、列生成法[16]等。此外，该问题的启发式方法主要有局部搜寻[11, 17]、禁忌搜寻[18～20]、进化算法[21]、混合元启发式方法[22]以及PSO算法[23]等。关于SDVRP及其扩展问题还可参考综述性文献[24,25]。国内对SDVRP的研究较少，近年来相关的研究有：陈靖等[26]考虑了车辆运载能力限制与客户产品新鲜度要求，对生鲜品的物流集配问题进行建模；王旭坪等[27]构建多约束条件下的同时集送车辆路径优化模型，满足了实际物流配送中客户对不同车型及服务时间的多样化需求；徐东洋等[28]考虑了多车场、多车型、多货品、客户间供需未匹配和取送货需求可任意拆分等因素，研究取送货车辆路径问题；卿东升等[29]研究了满载需求可拆分车辆路径规划问题，并采用粒子群算法求解。

总结已有文献可以发现：①VRP研究中大都假设客户需求不可分割，但这种假设与现实的物流配送场景不太符合，还会降低车辆的利用率，无法保证整个优化结果的适用性，所以研究SDVRP具有现实指导意义；②由于燃油车在部分城市道路上受限行政策影响，和其在配送过程中产生的环境污染问题，同时考虑到油价的增长，引入电动汽车到物流配送中顺应了时代的发展趋势。鉴于此，研究需求可拆分的电动汽车车辆路径问题，显得十分必要。此外，现有SDVRP和EVRP的求解算法，仅分别围绕需求拆分策略和换电充电策略进行算法设计，因此，同时实现兼顾这两类因素和协同这两种策略的算法也显得非常必要。本研究拟将EVRP与SDVRP相结合，研究E-SDVRP，并建立其相应的数学规划模型；运用基于列生成的分支定价算法对问题进行分解，推导出复杂的定价子问题目标函数，并设计相应的标签算法求解该问题的最优解。

2 问题概述和建模

2.1 问题概述

在图G=(C∪R∪{0},A)中，C为客户点集合，R为换电站集合，弧(i,j)∈A。考虑通过电动汽车从配送中心出发，给相应的顾客运输货品，每个顾客的需求可以被拆分，由多辆车共同配送，每辆车最多为同一个客户点配送一次。客户点i的货物需求量为qi；dij表示i点到点j的距离；cij表示电动汽车从点i到点j的行驶花费；换电站的位置已知，每次换电的费用为cB；K表示电动汽车集合，从配送中心出发的电动汽车的电量是满的，电动汽车的最大行驶里程(电池的最大容量)为B，最大载重量为Q。本研究的目标函数为使系统总配送成本最小。

2.2 建模

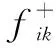
表1 E-SDVRP模型构建中的变量和参数

该模型描述如下：

(1)

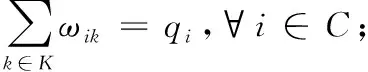
(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

j∈R∪C∪{n+1}，i≠j，k∈K；

(11)

(12)

(13)

j∈R∪C∪{n+1}，i≠j，k∈K；

(14)

(15)

(16)

xijk∈{0,1}，∀k∈K，(i,j)∈A。

(17)

其中，目标函数(1)表示最小化物流系统的总配送成本，包括电动汽车的行驶成本和换电成本；式(2)表示电动汽车运输给客户点i的货物量之和等于该点的需求量；式(3)是上文“k-分割圈”属性的数学表达；式(4)为电动汽车的数量约束；式(5)和式(6)确保每条路径弧的均衡；式(7)表示非负约束和车辆的载重限定；式(8)保证xijk与变量ωik的一致性；式(9)体现了车辆到达换电站时的载重量等于车辆离开换电站时的载重量；式(10)表示电动汽车到达客户点时的货物量减去离开该客户点时的货物量，为这辆车给该客户点的配送量；式(11)表示电动汽车货物流量的约束；式(12)表示电动汽车离开配送中心或换电站时，电池为满电状态；式(13)表示电动汽车到达和离开客户点时，电量相等；式(14)表示电动汽车离开点i和到达点j的电量约束；式(15)表示电动汽车k到达和离开点i时的电量在0到B之间；式(16)表示电动汽车k到达和离开点i时，车辆的载重量在0到Q之间；式(17)表示决策变量的0-1约束。

3 Danzig-Wolfe分解

以上数学模型通过Dantzig-Wolfe分解的方法可以分为主问题模型和子问题模型。

3.1 主问题模型

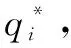
主问题模型构建如下：

(18)

(19)

(20)

(21)

θr∈{0,1}，∀r∈Rm；

(22)

θr∈Z，∀r∈Rs。

(23)

表2 主问题模型中的变量和参数

其中，目标函数(18)与函数(1)一致，计算系统的最小总配送成本；式(19)～式(21)与式(2)～式(4)的效用一致；式(22)及式(23)为0-1约束和整数约束。

3.2 子问题模型

根据对偶原理，可以定义子问题模型中的相关变量：πi表示式(19)的对偶变量，当i∈R时，πi=0；当i∈C时，πi表示配送客户的需求量；ρij表示式(20)的对偶变量，且ρij=ρji；β表示式(21)的对偶变量，则子问题模型构建如下：

(24)

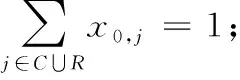
(25)

(26)

(27)

(28)

(29)

(30)

(31)

∀i∈R∪C∪{0}，j∈R∪C∪{n+1}，i≠j；

(32)

(33)

ωi≥0，ωi∈Z，∀i∈C；

(34)

xij∈{0,1}，∀(i,j)∈A。

(35)

其中，目标函数(24)表示寻找非负检验数最小的路径；式(25)～式(35)与式(5)～式(17)一致，保证子问题搜索的路径满足流量平衡、载重量、电量和需求可拆分约束。

4 模型求解

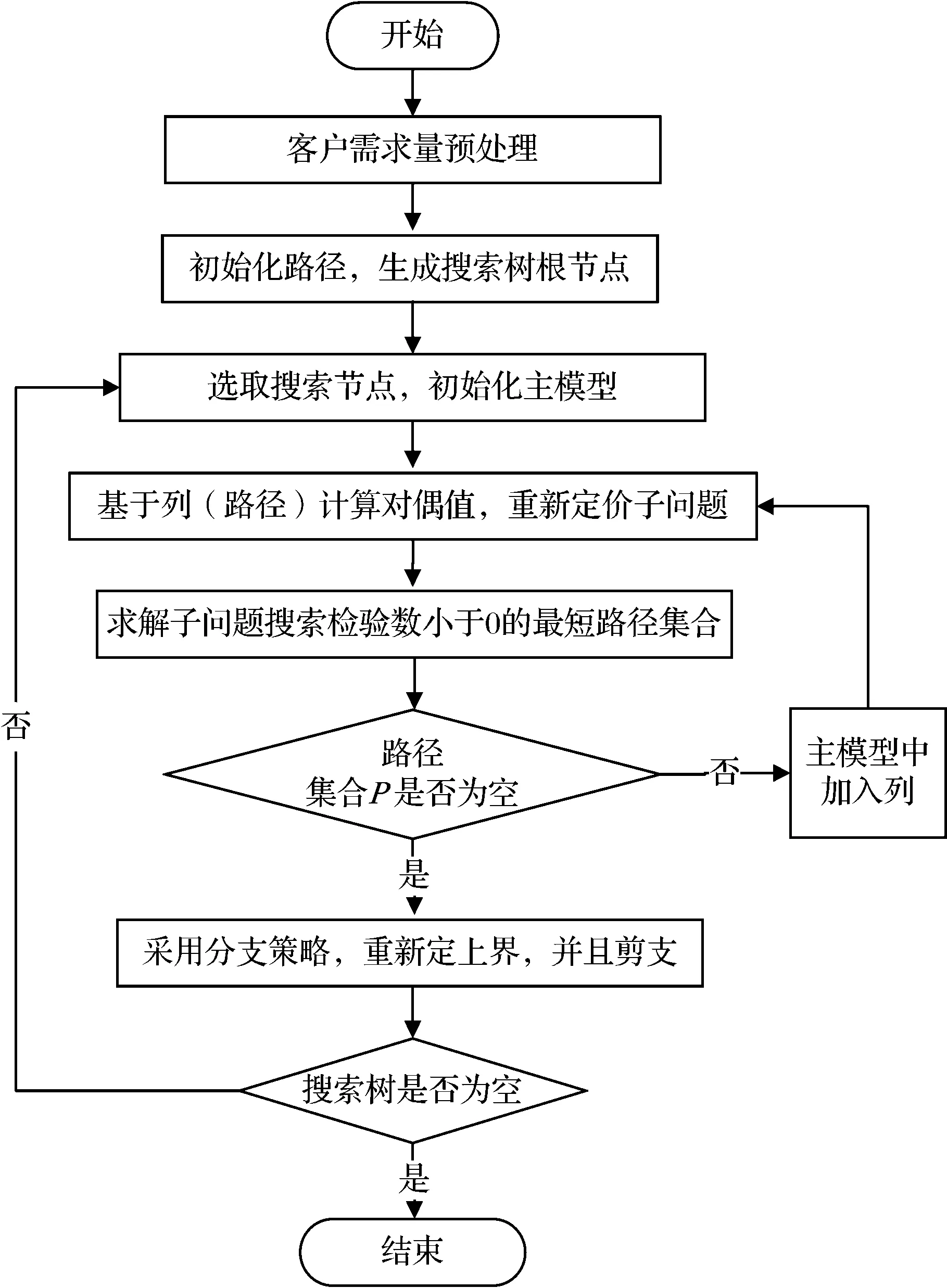
4.1 动态规划算法

4.2 分支策略与整数解

5 实验计算与分析

本部分使用的计算机核心参数为4核CPU，2.50GHz主频，8GB内存，算法采用单线程的JAVA代码实现。

5.1 实验数据

5.2 实验结果与对比分析

5.2.1模型及算法的验证分析

本研究将式(1)～式(17)转化为CPLEX程序来评估最优解的准确性。该部分使用IBM ILOG CPLEX 12.7求解该问题的10组小规模算例。如果CPLEX在3 600秒内没有得到全局最优解，则给出当前最优解。接着，把求得的结果与改进分支定价算法的计算结果作比较，测试结果见表3。由表3可见，CPLEX和改进分支定价算法的计算结果大致相同，模型及算法的准确性得以证明。

表3 小规模算例结果

5.2.2较大规模实验结果

为了验证E-SDVRP的求解算法具有一定的实用性，本研究进行了大规模实验数据的算法测试。算法在解决较大规模E-SDVRP的实例数据与实验结果见表4。

表4 较大规模算例结果

实验结果表明：问题规模变大，求解时间随之增加，本研究改进的分支定价算法都能在不同规模的数据集下求解现实场景的E-SDVRP，并得到问题的解，说明该算法的一般实用性。求解时间的增加与实验数据本身和问题复杂度相关，这可以通过一些数据预处理(如客户区域划分等)操作，保证算法运行时间在可接受的时间范围内。

5.2.3相关因素灵敏度分析

最大载重量和最大行驶里程是电动汽车最核心的两个指标参数，最大载重量的增加会导致车辆单位距离行驶成本的增加，最大行驶里程的增加会导致换电成本的增加，进而直接影响本研究模型的计算结果。由此，本研究将在最大载重量和最大行驶里程中考虑上述两种成本，分析参数变化对结果的影响。

为了保证实验的一般性，本研究在较大规模算例中选取5组算例进行测试，分别命名为A、B、C、D和E。该组算例数据汇总后的情况为：客户点数量为50，换电站数量为20，车辆数量为13，电动汽车的最大载重量分别为25、28、21、25、27，电池的最大行驶里程为291.15。

(1)电动汽车的最大载重量Q与单位行驶成本cij为了研究电动汽车的最大载重量和行驶成本对计算结果的影响，将最大载重量设为相对初始值逐渐增加0%、25%、50%、75%和100%，单位距离的行驶成本根据实验数据的设定原则相应地进行变化，实验结果见表5。

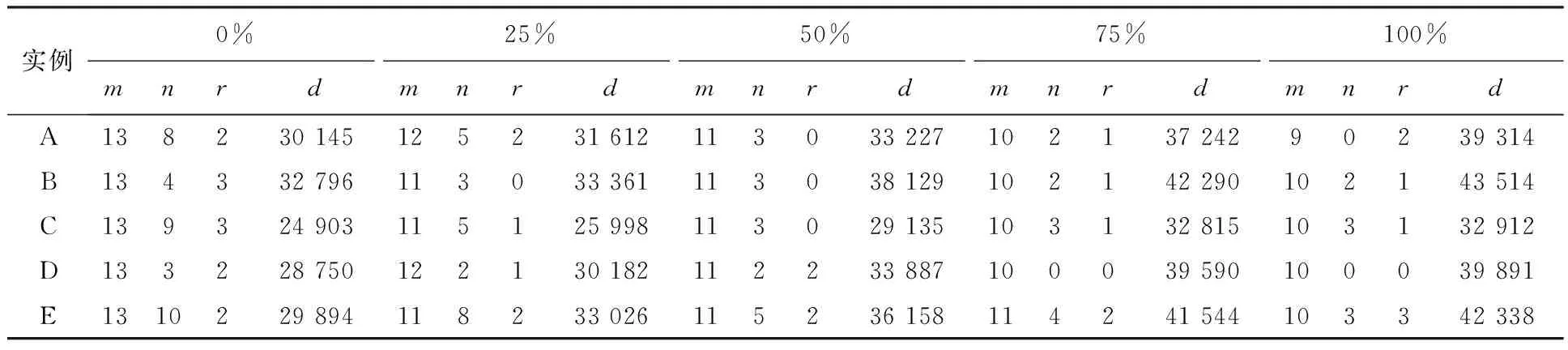
表5 电动汽车最大载重量和行驶成本的灵敏度分析

实验结果表明：客户需求被拆分的数量和电动汽车的数量，随着最大载重量和行驶成本的逐渐增加，呈减少的趋势。当其最大载重量增加到一定程度后，客户的需求不需要拆分，可以一次配送即能满足，问题将转化为电动汽车的VRP问题。在网路拓扑结构和最大行驶里程已确定的情况下，电动汽车最大载重量的增加，将导致拆分的需求可以选择最近的电动汽车进行配送，配送里程会相应地减少，或者电动汽车可能借助附近的换电站增长行驶里程来服务更多的客户点，导致整体配送车辆数量的减少，经过换电站的数量增加。但因为行驶里程成本占总成本的比重比较大，单位距离行驶成本的增加，会导致整体配送成本呈现逐渐增长的趋势。

(2)电池的最大行驶里程B与单次换电成本cB参考上述参数设置方法，将B设为相对初始值逐步增长0%、25%、50%、75%和100%，换电成本cB根据实验数据的设定原则相应地进行变化，实验结果见表6。

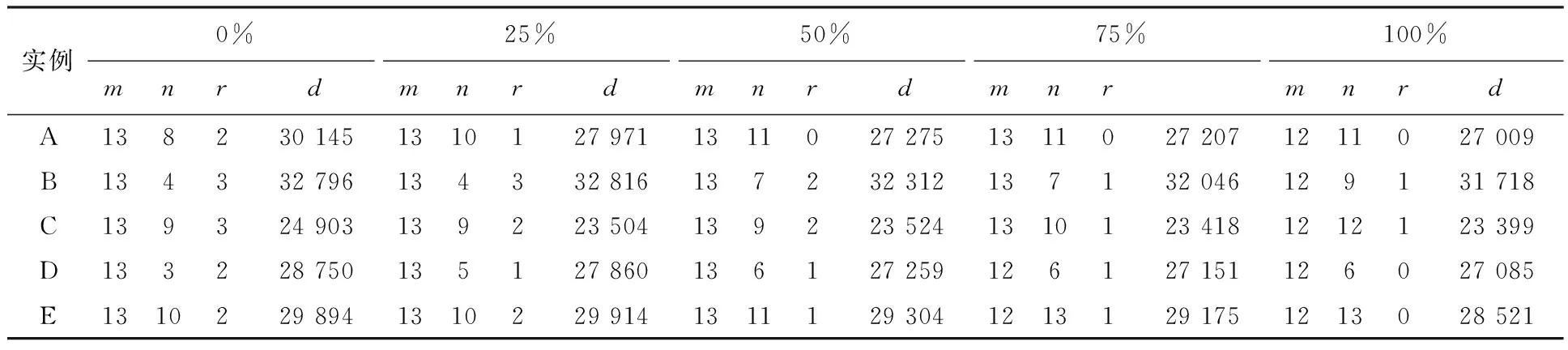
表6 电动汽车最大行驶里程和换电成本的灵敏度分析

实验结果表明：电动汽车经过换电站的数量和所需的车辆数量，随着电池的最大行驶里程和换电成本的逐渐增加，呈减少的趋势；而配送总费用因为换电成本的增加和配送里程的减少之间的平衡，出现上下波动的情况。当其最大行驶里程增加到一定程度后，车辆经过换电站的数量将减少，客户需求被分割配送的数量将在访问换电站数量变少时呈现增多的趋势，然后再呈现比较平稳的趋势。相对于需求不可拆分场景，需求可拆分的场景通过拆分客户需求配送多次的方式，能够减少车辆的数量，提高车辆满载率。实验中，电池的最大行驶里程的增加会让电动汽车可以服务更多的客户点，由于车辆数量和整体载重量的限制，会选择更加合适的电动汽车进行拆分配送，特别是当经过一个换电站，能够服务更远的客户，会导致车辆数量的减少，原来从车场出发服务客户的车辆，直接在最大载重量的限制下由换电站出发的车辆去服务更多的客户，整体配送里程也跟着降低。同时，电池的最大行驶里程的增加导致途径的换电站数量减少时，减少的换电费用会触发新的需求拆分进行调整，可能导致原有配送路线进行大的调整和客户需求拆分数量增长。

6 结语

本研究探讨E-SDVRP，建立了相应的数学模型，并根据该问题客户需求可分割和电动汽车有行驶里程和车辆数量限制等特点，设计了相应的求解算法。此外，基于某大型电商网站的真实案例数据，验证了本研究改进的分支定价算法可以有效地加速算法求解。对该问题的重要参数做了灵敏度分析，发现最大载重量增加相对于最大行驶里程增加，对总成本的影响会更大一些。

进一步的研究可以从以下两点着手：①在求解算法中加入启发式算法，以求解更大规模的算例；②更多地考虑物流企业的实际配送情况，把路网的不确定性加入到模型中，研究路网不确定性的情境下客户需求可分割的电动汽车车辆路径问题。