考虑固定和凸变动成本以及两类需求的动态生产策略
2020-12-24刘志学
赵 玲 刘志学
(华中科技大学管理学院)
1 研究背景
随着经济社会的快速发展,作为供应链中关键节点的制造商遇到的库存决策问题也变得更加复杂,不仅要面对由上游公司或自身导致的生产成本结构的复杂性,而且要面对来自下游顾客需求的多样性。对于一些行业(如化工业、印刷业等)的制造商而言,其生产成本可能不是简单的固定与线性变动类型,而是更加一般的固定与分段线性凸变动成本结构,即边际成本会随生产量的增加而升高。例如,当制造商的生产量超出一定水平时,需要支付的单位能源(如电力、天然气等)成本更高,同时其产生的碳排放量会超出规定额度,因而需要额外购买碳排放配额。
一些制造商在面对固定与凸变动生产成本的同时,也会面对不同类型的顾客需求,即确定性需求和随机需求。比如,为了提高经营效益,制造商通常会与其大客户签订长期合同,保证每隔一段时间都会向客户交付一定数量的产品。供应合同的需求必须完全满足,否则制造商将会失去客户甚至信誉受到损害。同时,如果制造商有多余的库存,还可以满足其他小客户的订单。由此,供应合同的需求可以看作是必须满足的确定性需求,而来自其他小客户的临时需求则视为随机需求,可以延期交货。
到目前为止,关于考虑固定与凸变动生产成本库存问题的研究中,学者们大多聚焦于需求为随机的情形,而针对确定性和随机性需求同时存在情形的研究非常少。然而,在企业实际运作中,两种类型需求同时存在的情形很常见。基于此,本研究将讨论当制造商同时面对固定与凸变动生产成本和两类需求时,怎样制定生产策略才能使制造商的总期望成本最小。对于这个问题,首先建立考虑固定和凸变动成本以及两类需求的随机动态规划模型,然后通过理论分析得到最优策略,最后通过数值实验验证与确定性需求有关的约束条件对最优策略的影响。
2 文献回顾
在库存管理类文献中,很多学者考虑的补货成本是线性结构,如HU等[1]、慕银平[2]、陈啟等[3]以及温宗良等[4]。同时,也有不少学者对有关固定补货成本的问题感兴趣。SCARF[5]最早对考虑固定补货成本的周期盘点的库存模型进行探讨,目标是通过决策每周期的补货量最小化有限计划期内的总期望折扣成本。通过引入K-凸函数的概念,SCARF[5]证明了延期交货情形下简单的(s,S)策略最优,其中s是区分补货与不补货的界点,S是补货水平。之后,有许多学者研究类似的考虑固定成本的模型,如VEINOTT[6]、CHEN等[7,8]、HUH等[9]、CHAO等[10]、CHEN等[11]、PERERA等[12]以及高登等[13]。然而,这些文献讨论的变动成本大多仅为简单的线性结构,只有很少的研究讨论凸变动补货成本,如LU等[14,15]和HU等[16]。在有关固定与凸变动补货成本的研究中,与本研究相关的为文献[14,16]。这两篇文献都研究了考虑固定及凸变动补货成本的随机动态规划模型,通过证明最优值函数的强(K,c,q)-凸性或比该性质更一般的κ-凸性,对最优策略进行部分刻画,其中,K、c、q和κ分别表示固定成本、变动成本参数、补货点和补货成本函数。与这两篇文献相比,本研究考虑的最优化问题的限制条件更加复杂,这不仅依赖于制造商的初始库存,而且还依赖于当期的确定性需求,因而这两篇文献的结论不再适用于本研究讨论的模型。为了解决这个问题,证明(K,c,q)-凸函数经过与确定性需求相关的约束情形下的最优化运算之后依然呈(K,c,q)-凸性,也是本研究的主要贡献之一。应用该性质,可以部分刻画最优策略。虽然LU等[14]以及HU等[16]也部分刻画了最优策略,但本研究用于刻画最优策略的界值依赖确定性需求。特别地,当初始库存低于确定性需求时,制造商必须进行生产,而且其生产水平高于确定性需求。
与本研究模型相关的另一个文献流是和多种类型需求相关的随机动态库存问题,其中按优先权对顾客需求进行分类的文献较多,如DURAN等[17]、ZHOU等[18]以及ZHOU等[19]。大部分文献仅考虑随机性需求,然而,也有少量文献同时考虑确定性和随机性需求,如FRANK等[20]以及汪达钦等[21]。在同时考虑确定性与随机性两种需求的随机动态库存模型中,与本研究最相关的是文献[22,23]。这两篇文献都假设确定性需求必须满足,随机需求可以延期交货;且考虑了前一周期的延期交货必须在当前周期满足的情形;用于刻画最优策略的界值都依赖于确定性需求。但本研究与这两篇文献有3个方面的关键不同:①关于补货成本的结构,本研究考虑的是固定与凸变动成本,而SOBEL等[22]以及CHEN等[23]考虑的是固定与线性变动成本(这只是本研究的一种特殊情况);②关于最优值函数,本研究证明最优值函数具有(K,c,q)-凸性,这比已有研究得到的K-凸性更一般;③本研究最优策略的结构更加复杂,并不是简单的改进的(s,S)库存策略。
3 模型建立
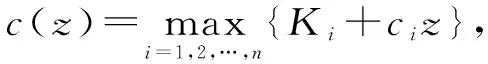
(1)
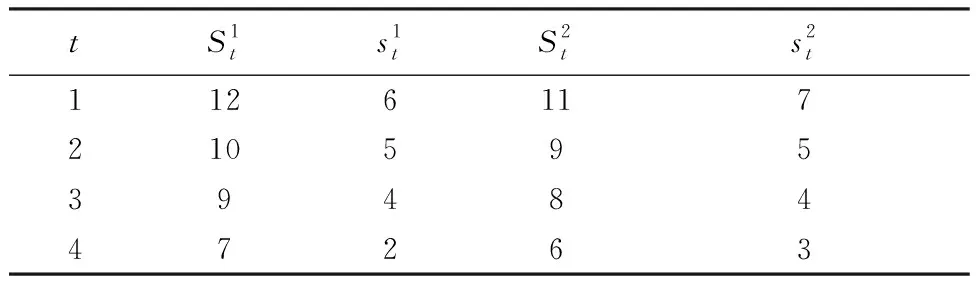
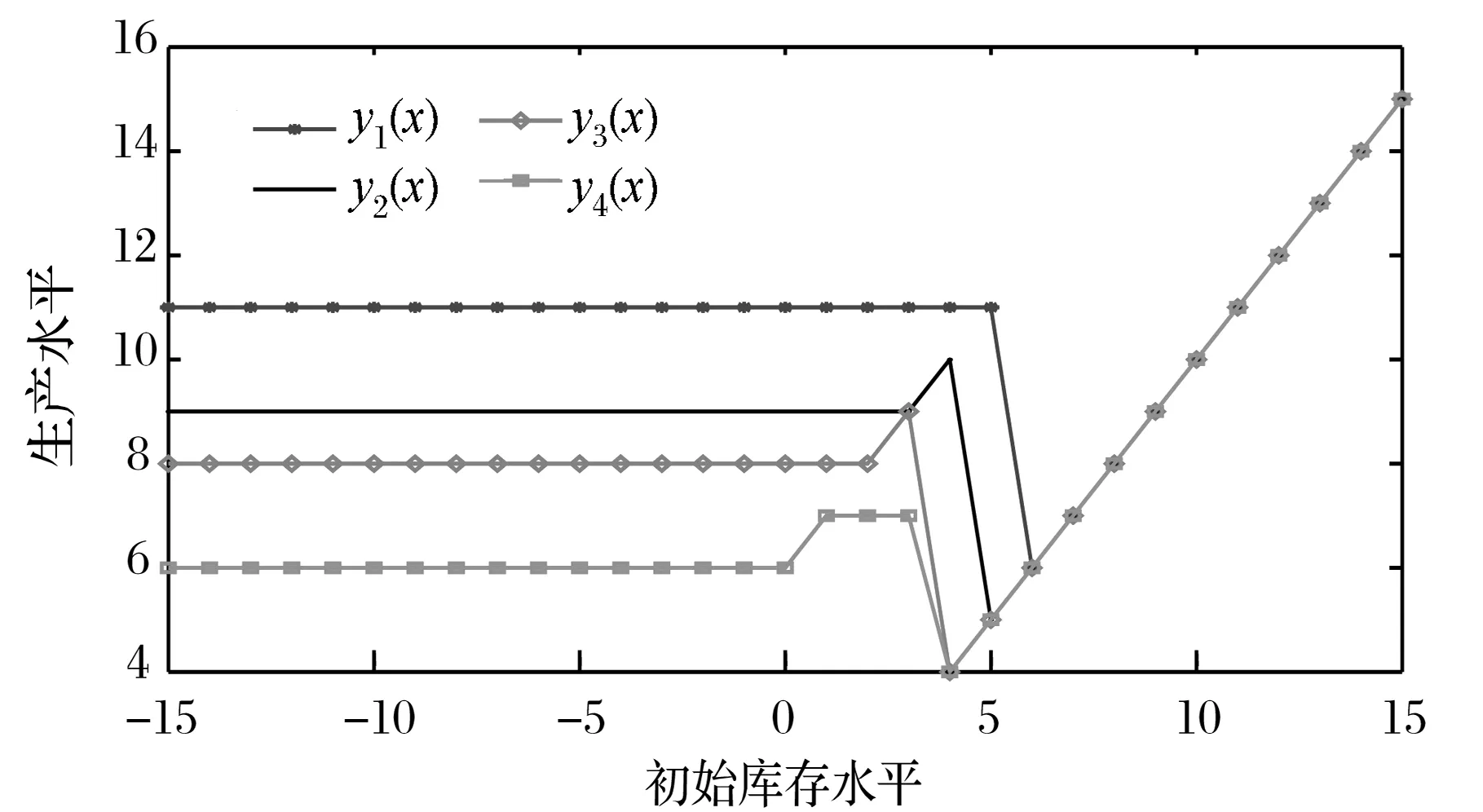
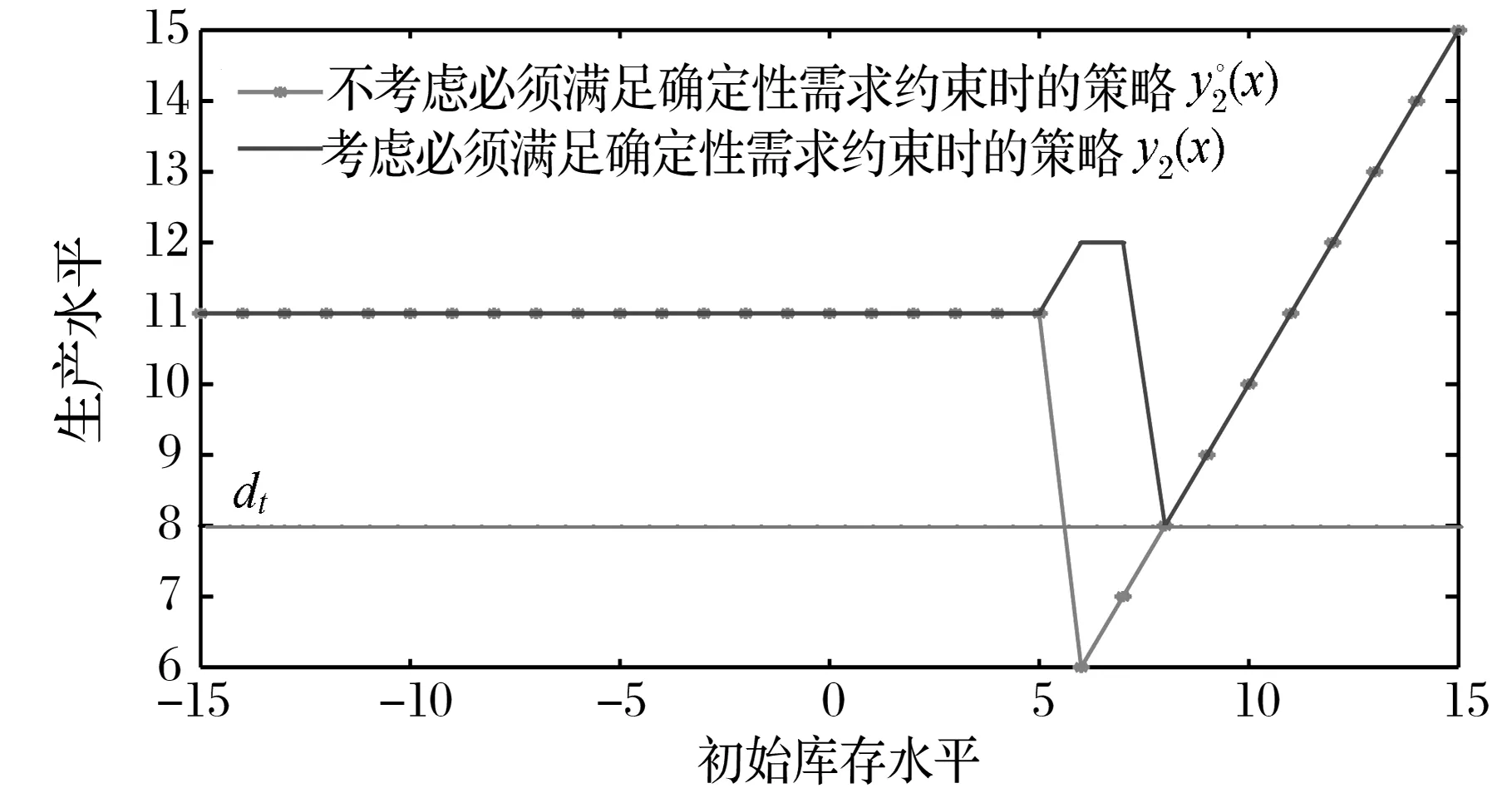
式中,0=q0 假设生产提前期为零,那么当制造商生产z单位产品之后,产品的库存水平立即变为y=x+z,即生产水平。接下来,用现有的库存y去满足顾客需求。与文献[22]中的一种情形相似,本研究假设未满足的随机需求可以延期交货,而且当确定性需求dt>0时,必须在当前周期完全满足确定性需求和前一周期的延期交货。注意到如果制造商的初始库存x<0,那么前一周期的延期交货量为-x,否则为0;而且,生产水平不低于初始库存,即y≥x。由此,生产水平y所在的范围It(x)满足: It(x)={y:当dt>0时y≥x∨dt; 当dt=0时y≥x}, (2) 式中,x∨y=max{x,y}。假设满足需求后的剩余库存依然可以用来满足后续周期的需求,又因为未满足的需求可以延期交货,所以制造商在周期末的库存水平为y-dt-εt。记非负系数h和p分别为单位库存持有成本和单位库存短缺成本,而且y+=max{y,0},y-=max{-y,0}。那么,制造商在第t周期产生的库存持有/短缺成本为H(y-dt-εt),其中H(y)=hy++py-。假设单位变动惩罚成本大于单位变动生产成本,即p≥ci,i=1,2,…,n。这个假设在文献中很常用,如FOX等[24]。 记折扣因子为γ∈[0,1],作用于随机变量εt的期望算子为E。制造商的目标是最小化其有限计划周期内总期望折扣成本。给定第t周期的初始库存x,第t周期到最后一周期的总期望折扣成本为 c(y-x)+gt(y)},t=1,2,…,T, (3) 式中,gt(y)=EH(y-dt-εt)+γEft+1(y-dt-εt),且fT+1(x)=0。 (4) 给定t=1,2,…,T及i=1,2,…,n,下面证明如果ft+1(x)在区间(-,0]上递减,那么由Ht(y)的定义可知,当y≤0时,H(y)+γft+1(y)+ciy=(-p+ci)y+γft+1(y)。注意到p≥ci且ft+1(x)在(-,0]上递减,因此,当y≤0时,H(y)+γft+1(y)+ciy递减。又由的定义知 ci(y-dt-εt)]+ci(dt+Eεt), (5) 现在只需要证明对任意的t=2,3,…,T,ft(x)在区间(-,0]上递减。由于dt>0,因而It(x)={y:y≥x∨dt}。于是,由ft(x)的定义可知,当x (6) 记y0是x=x0时问题(3)的最优解,那么对任意的x0 ft(x0)=K+c(y0-x0)+gt(y0)≥ K+c(y0-x1)+gt(y0)≥ft(x1)。 (7) 式(6)及c(z)的单调性可以确保式(7)成立。可见,当x 这一部分将分别对最优化问题(3)在单期情形和多期情形下的最优解进行讨论。 单期问题对应于问题(3)在第T周期的情形。单期情形下最优解的刻画可以用于处理季节性或易变质产品的库存问题。为便于刻画最优解,首先定义 (8) 定理1当t=T且dt>0时,存在界值st,使得问题(3)的最优解yt(x)满足: (9) (10) c(y-x)+gt(y)}=ft(x), (11) 综上可知,式(9)成立。 定理1对单期情形下的最优策略进行完全刻画。当需要生产时,生产水平yt(x)随着初始库存x的增加而提升,这说明制造商在一个周期开始时的产品越多,生产结束时产品的库存水平越高。由定理1还可知,生产水平yt(x)高于确定性需求dt,这个结论符合模型中确定性需求必须满足的假设。此外,当界点st低于确定性需求dt时,dt就是区分是否进行生产的界值;否则,本定理的结论与文献[14]的定理1一致。 当t=T时,最优解的结构依赖于函数gt的凸性;当t 下面先引入强(K,c,q)-凸性的定义[14],其中,c=(c0,c1,…,cn),q=(q0,q1,…,qn)。给定K≥0,0=q0 f(x-u-v)],∀u≥0,v>0,z≥0 , (12) 则f(x)是强(K,c,q)-凸函数。本研究将通过证明最优值函数的强(K,c,q)-凸性刻画多期情形下的最优解。 下面给出有关强(K,c,q)-凸函数的一些性质。 引理1①若f(x)是凸函数,则f(x)是强(K,c,q)-凸的,其中,K≥0,0=c0≤c1<… (13) 证明因为引理1的前4个结论都来自LU等[14]的研究,所以下面只需要证明⑤成立,即对于任意的u,v≥0和x0+u≤x1-v,有 v[f(x0+u)-f(x0)]+u[f(x1-v)-f(x1)]≤ u[c(v)-c1v+K]。 (14) 对于式(14),根据x0,x1与两个集合E,O之间的关系分3种情况,其中,E={x:f(x)=g(x)}且O为E的补集。为方便描述,记式(13)在x=xi处的解为yi,而且令zi=yi-xi,i=0,1。则对于i=0,1, f(xi)=K1{zi>0}+c(zi)+g(xi+zi),xi+zi≥d, (15) 其中,当xi∈E时,zi=0;当xi∈O时,zi>0。 (i)假设x0,x1∈O(这种情形下构造可行解的方法类似于文献[16]中的命题1)。为了简便,令λ=0∨[(z0-z1)/(x1-x0)]∧1,这与0≤u,v≤x1-x0一起可以确保z0-λu,z1+λv∈[z0∧z1,z0∨z1]。因为zi≥0,所以 z0-λu≥0,z1+λv≥0 。 (16) λ的定义还可以确保 x1-v+z1+λv≥x0+u+ z0-λu≥x0+z0,∀0≤λ<1 。 (17) 于是,式(16)和式(17)及xi+zi≥d可以确保对于任意的λ,都有 (18) 这说明x0+u+z0-λu和x1-v+z1+λv分别是问题(13)在x=x0+u和x=x1-v处的一个可行解,因此, (19) 将式(19)及f(x)在x0,x1处的表达式代入目标不等式,可得 δ+[uc(z1+λv)+vc(z0-λu)]- [uc(z1)+vc(z0)]≤u[c(v)-c1v+K], (20) 式中,δ=v[g(x0+u+z0-λu)-g(x0+z0)]+u[g(x1-v+z1+λv)-g(x1+z1)]。于是,下面只需要证明不等式(20)成立。 因为c(z)是凸函数而且z0-λu,z1+λv∈[z0∧z1,z0∨z1],所以 (21) 由式(21)可得,uc(z1+λv)+vc(z0-λu)≤uc(z1)+vc(z0)。可见,要证明目标不等式成立,只需要证明δ≤u[c(v)-c1v+K]。若λ=1,则由δ的定义可知δ=0;而若0≤λ<1,则由λ的定义可知,x0+z0 (1-λ)δ= (1-λ)v[g(x0+u+z0-λu)-g(x0+z0)]+ (1-λ)u[g(x1-v+z1+λv)-g(x1+z1)]≤ (1-λ)u[c(v-λv)-(1-λ)vc1+K]。 (22) 又由于0<1-λ≤1且c(z)递增,因而δ≤u[c(v)-c1v+K],故目标不等式成立。 (ii)假设x0∈E。那么yt(x0)=x0≥d。又因为x1>x1-v≥x0+u>x0,于是在这4点处, (23) 可见,由g(x)的强(K,c,q)-凸性及引理1④可知目标不等式成立。 (iii)假设x0∈O,x1∈E。下面分z0≥u和z0 假设z0≥u。因为x1∈E,所以由E及f(x)的定义可知x1≥d。注意到x0+z0≥d,z0≥u且v≥0,因此,(x0+u)+(z0-u)≥(x0+u)∨d,(x1-v)+v≥(x1-v)∨d。这说明(x0+u)+(z0-u)和(x1-v)+v分别是问题(13)在x=x0+u和x=x1-v处的一个可行解。于是,有 (24) 将式(24)及f(x)在x0,x1处的表达式代入目标不等式可得v[c(z0-u)-c1(z0-u)-(c(z0)-c1z0)]+u[K+c(v)]≤u[c(v)+K]。因为c(z)-c1z递增,所以该不等式显然成立,故目标不等式成立。 由上述3种情况可知,目标不等式成立。 引理1说明凸函数也是强(K,c,q)-凸的;经过期望运算、加法运算、数乘运算和最优化运算之后,强(K,c,q)-凸性依然成立。下面应用这些性质,证明问题(3)的最优值函数是强(K,c,q)-凸的。 命题2对于任意t=1,2,…,T,问题(3)中的最优值函数ft(x)都是强(K,c,q)-凸的。 证明用关于t的归纳法证明ft(x)是强(K,c,q)-凸的。当t=T+1时,因为ft(x)=0,所以由引理1①可知,ft(x)是强(K,c,q)-凸的。假设ft+1(x)是强(K,c,q)-凸的,下面证明ft(x)的强(K,c,q)-凸性。注意到H(y)的凸性与引理1①一起可以保证H(y)是强(K′,c′,q)-凸的,其中K′=0,c′=0。这与ft+1(x)的强(K,c,q)-凸性、引理1②和③一起可以确保gt(y)=EH(y-dt-εt)+γEft+1(y-dt-εt)是强(K,c,q)-凸的。注意到当dt=0时,It={y:y≥x};当dt>0时,It={y:y≥x∨dt}。由此,gt(y)的(K,c,q)-凸性、ft(x)的定义以及引理1④和⑤一起可以保证ft(x)的强(K,c,q)-凸性。 命题2说明,问题(3)的最优值函数ft(x)是强(K,c,q)-凸的。又因为当dt=0时It={y:y≥x},所以当dt=0时最优策略的结构与文献[14]中给出的一致,因此,下面仅用ft(x)的强(K,c,q)-凸性对问题(3)在dt>0时的最优解yt(x)进行刻画。为简便,定义Ot为一个状态集,使得当初始库存在这个集上时进行生产是最优的,即Ot={x:yt(x)>x}。 证明由dt>0及集合Ot的定义可知,最优化问题(3)等价于 (25) 这说明要证明yt(x)在集合Ot上是递增的,仅需证明问题(25)最优解的递增性即可。注意到c(z)是凸函数,这与文献[25]中的引理2.6.2(b)一起,可以保证函数c(y-x)关于(x,y)是次模的,进而可以得到问题(25)中目标函数的次模性。又因为限制集合{y:y≥x∨dt}关于x是递增的,所以由文献[25]中的定理2.8.2可知,问题(25)的最优解随x递增。故yt(x)在集合Ot上递增。 接下来,分3种情况讨论最优解yt(x)的取值范围。 ②由Ot的定义可知,对任意的x∈Ot都有最优解yt(x)>x。又由ft(x)的定义可知,对任意x,最优解yt(x)≥dt。这说明当x 在下面所有的数值算例中,令折扣因子γ=0.99,变动成本参数n=2,c1=0,c2=0.5,K1=0,K2=-3,q0=0,q1=6,单位库存持有成本h=4,单位缺货惩罚成本p=2,周期总数T=4,随机需求在集合{0,1,…,10}上均匀分布。 (26) 其中 (27) 表1 不同周期下的界值 (28) 这说明t=T时,定理1分析的最优解的结构与图1完全一致。此外,由图1的4种情形也可见,当需要生产时,生产水平yt(x)随初始库存水平x递增;生产水平都高于确定性需求,存在一个界点,使得当初始库存高于这个界点时就不需要生产。这些都与定理1 和定理2 中给出的结论一致。 对于同时考虑固定与凸变动成本和两类需求的单产品动态生产控制问题,本研究首先建立随机动态规划模型,然后证明最优值函数具有强(K,c,q)-凸性,并通过该性质得到最优生产策略的部分刻画,最后通过数值实验验证确定性需求对最优策略的影响。本研究得到以下主要结论:①当初始库存水平低于确定性需求时,制造商的生产水平会随初始库存水平递增,而当初始库存水平高于某个界值时,则不需要生产;②数值实验表明当忽略确定性需求必须满足这个假设时,确定性需求(如来自订购合同的需求)有可能不会得到满足,而且最优策略的结构会发生较大的变化。这说明制造商在进行生产决策时,需要充分考虑确定性需求带来的影响;否则它会因未满足确定性需求而失去大客户,甚至损害信誉。这些研究成果将为制造商应对生产成本结构的复杂性和下游顾客需求的多样性、降低其长期运营成本提供有效指导。应该指出的是,本研究假设制造商的生产提前期为零,后续将对提前期不为零的情形进行讨论。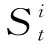
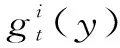
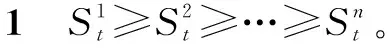
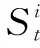
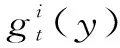
4 模型分析
4.1 单期情形下的最优策略
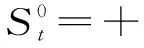
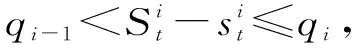

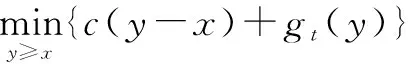
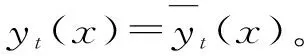
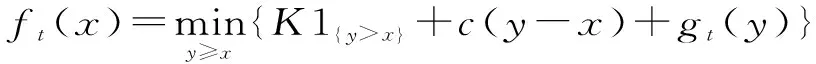
4.2 多期情形下的最优策略
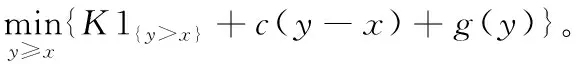

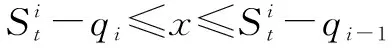

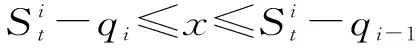
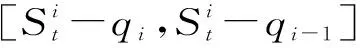
5 数值分析
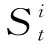
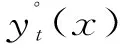
6 结语
