液压支架平衡缸的模糊自适应PID控制研究*
2020-12-24白淑江袁红兵廉自生
白淑江,袁红兵,高 飞,廉自生
(太原理工大学 机械与运载工程学院,山西 太原 030024)
0 引 言
作为综采工作面的重要设备之一,液压支架起着支撑工作面顶板,为井下工作人员提供安全工作空间的重要作用。在支护过程中,支架与围岩的耦合关系十分复杂,片帮以及基本顶的断裂现象时有发生,常常导致支架顶梁的俯仰角发生变化,出现“低头”或“高射炮”失稳的现象,降低了支架支护的稳定性[1]。因此,需不断调节平衡缸长度,使得顶梁的俯仰角保持在合理的范围内,这对平衡缸位置控制的响应速度和抗干扰能力提出了更高的要求。
近年来,液压支架信息感知和自适应控制成为了研究的热点。任怀伟等人[2]设计了一种包含速度补偿的RBF神经网络控制器,通过不断调节立柱和平衡缸的伸缩长度,保证支护状态下液压支架顶梁具有良好的稳定性。此后,他们[3]基于变论域模糊控制方法,提出了一种液压支架与围岩耦合自适应支护控制策略,根据外界环境的变化自主调节液压支架各项参数,很大程度上提高了液压支架的适应性,保证液压支架处于合理的支护状态。杜毅博等人[4]进行了液压支架状态信息快速获取和模糊综合评价方法的研究,该研究为液压支架支护状态监测和自适应控制提供了技术保障。
由实际支护过程可知,该系统是一种时变且扰动较多的非线性系统,因此预先设定的PID参数往往不能满足各种工况的需求[5,6]。为了解决这个问题,将模糊理论引入控制系统中。模糊自适应PID算法是以模糊理论为基础的控制算法,不需要精确的数学模型,而是根据实际过程中系统的状况对PID的相关参数进行实时自主调节。因此,该算法对受控对象的时变和非线性具有较好的适应能力,能够使得控制系统具有良好的的静态特性和动态特性[7-9]。
以液压支架平衡缸位置控制作为研究对象,笔者设计一种基于模糊PID算法的控制系统。
1 液压支架平衡缸系统分析
液压支架总体结构示意图如图1所示。
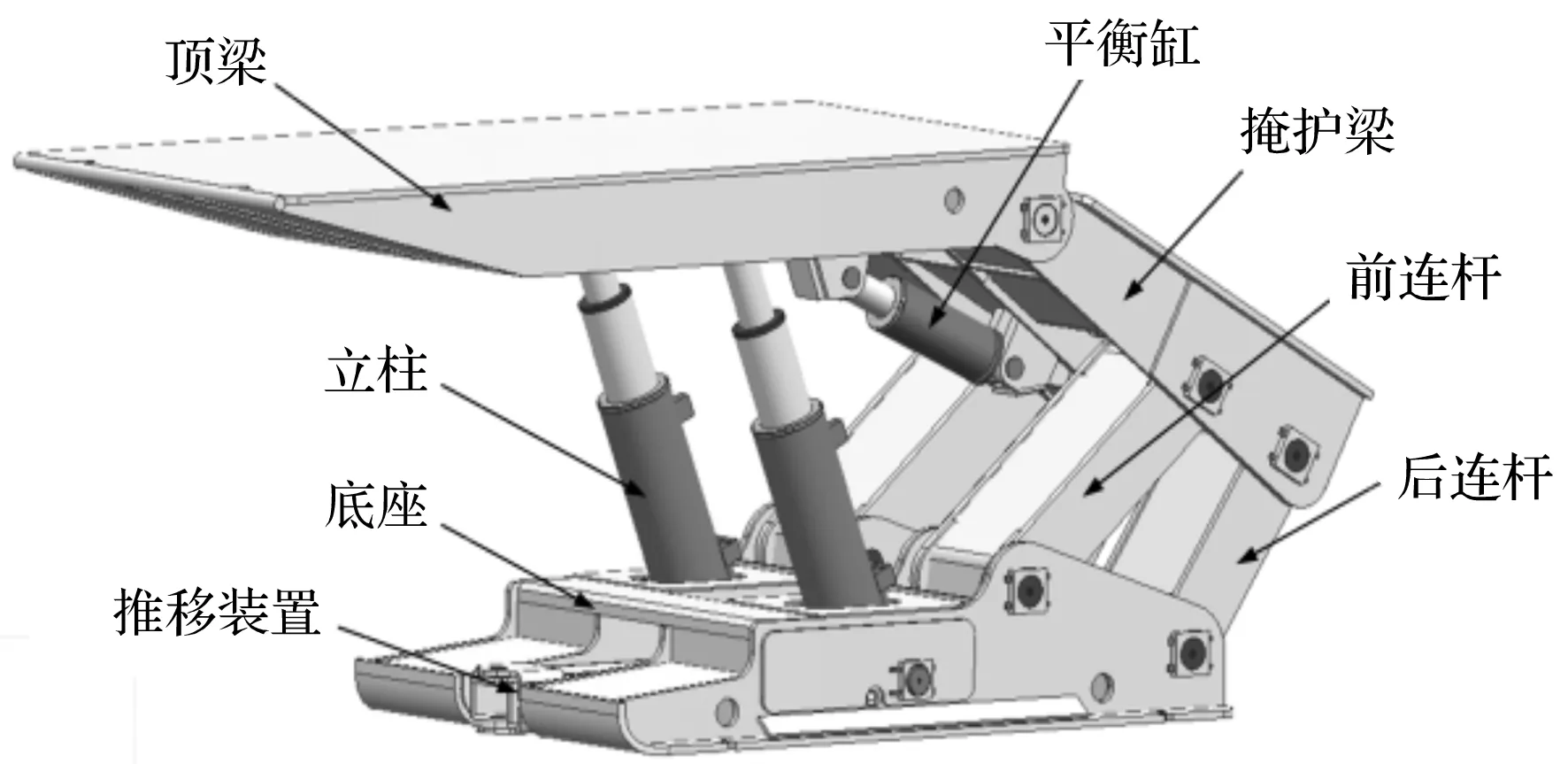
图1 液压支架总体结构示意图
系统由顶梁、底座、掩护梁、立柱、平衡缸和推移装置等组成。
1.1 控制系统数学模型
阀控非对称缸结构原理图如图2所示。
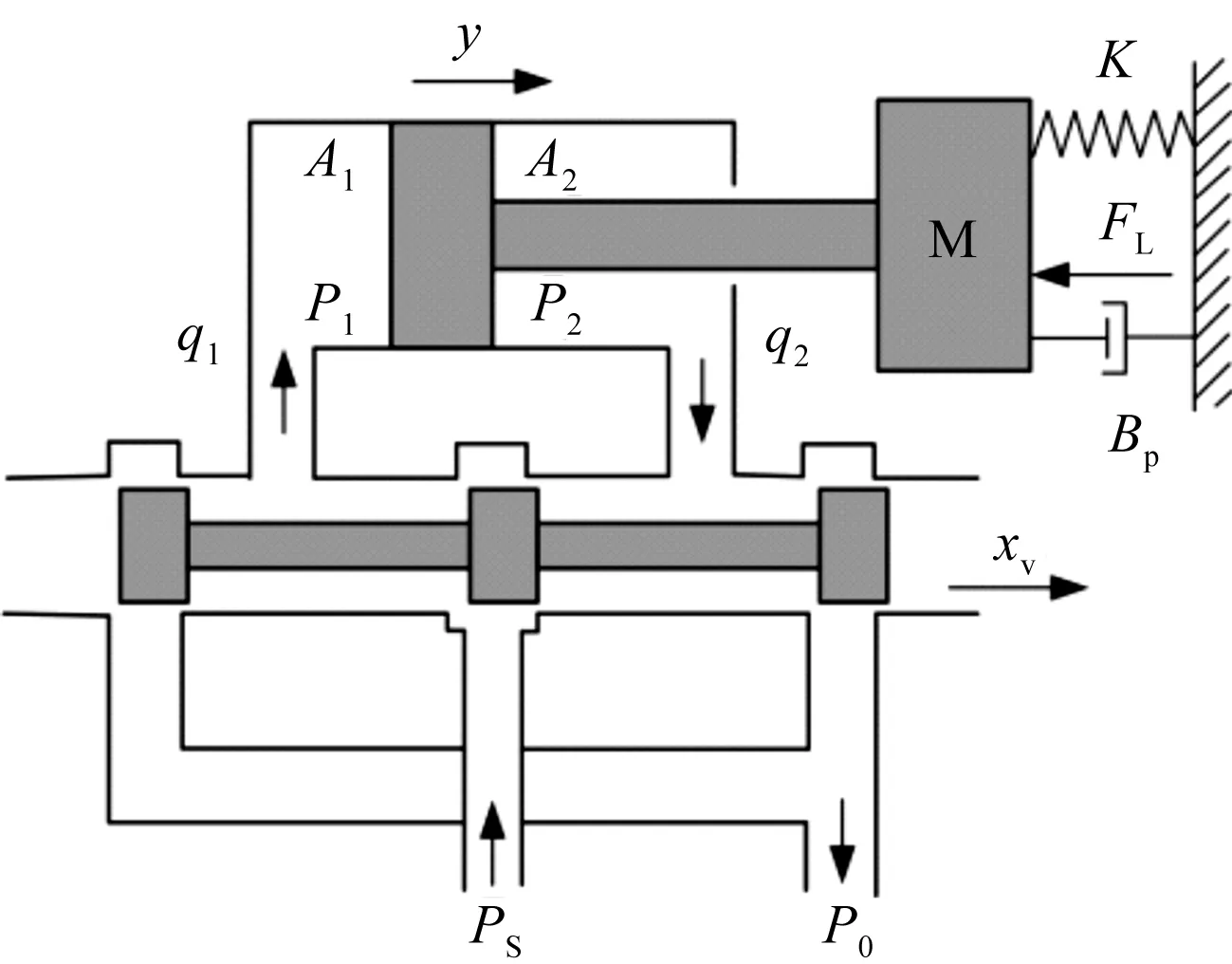
图2 阀控非对称缸结构原理图Ps—供油压力;P0—回油压力;A1—无杆腔活塞作用面积;q1—无杆腔流量;K—弹性系数;BP—负载粘性阻力系数;A2—有杆腔活塞作用面积;P1—无杆腔压力;M—液压缸负载质量;q2—有杆腔流量;xv—阀芯位移;y—液压缸的位移;P2—有杆腔压力;FL—外部负载力
图2中,笔者假定:(1)油路管道对称,且忽略管道中的压力损失;(2)供油的油温、密度、体积模量等参数均是常数;(3)供油系统为恒压。
由于非对称缸结构的非对称性,建立数学模型时要区分阀芯移动的方向,不同的移动方向会使得各项增益系数发生改变[10,11]。
当阀芯右移时,阀控缸的动态特性可由阀的流量方程、流量连续性方程以及液压缸力平衡方程表述,分别如下列各式所示:
QL=Kqxv-KcPL
(1)
(2)
(3)
式中:QL—负载流量;PL—负载压力;Kq—流量增益系数;Kc—流量压力系数;Cie—液压缸等效泄漏系数;Cf—液压缸附加泄漏系数;βe—弹性体积模量;Vt—等效总容积;Mt—活塞及负载折算到活塞上的总质量;Ap—液压缸活塞有效面积。
笔者对式(1~3)进行拉普拉斯变换,并联立。假设该系统只存在惯性负载,忽略弹性负载[12,13],则可得非对称阀控缸系统的传递函数为:
(4)
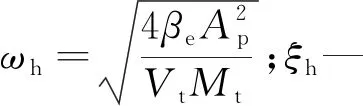
液压缸的传递函数为:
(5)
比例方向阀视为二阶振荡环节,其传递函数为:
(6)
式中:ωv—电液比例方向阀的固有频率;ξv—比例方向阀的阻尼比。
比例放大器的传递函数为:
(7)
式中:i(s)—比例放大器的输出电流;u(s)—比例放大的输入电压。
位移传感器传递函数为:
uf(s)=y·Kf
(8)
式中:uf—反馈电压;y—液压缸活塞位移;Kf—位移传感器的增益。
由式(5~8)可得系统传递函数框图,如图3所示。
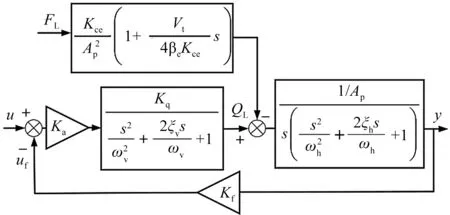
图3 系统传递函数框图
1.2 平衡缸液压系统仿真模型
在AMESim环境下,笔者搭建了液压支架平衡缸液压系统模型,并且创建了一个Simulink接口模块。
AMESim平衡缸液压系统模型图如图4所示。
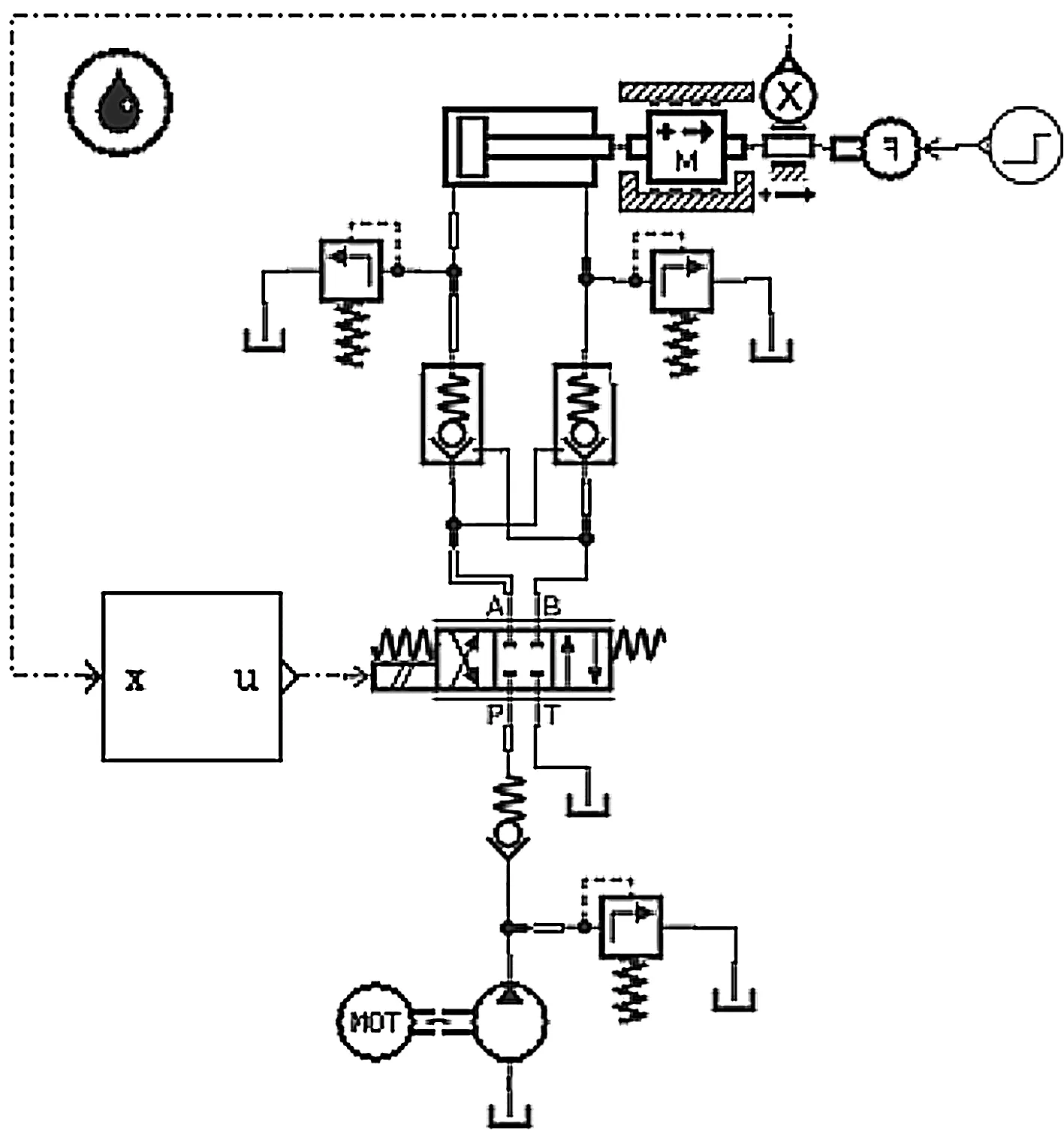
图4 AMESim平衡缸液压系统模型图
在AMESim/parameter模式下,笔者设定系统元件的主要参数为:
平衡缸内径为98 mm,活塞杆直径为70 mm,行程为0.22 m;方向阀额定流量为60 L/min,泵流量为300 L/min,负载重量为500 kg,供液压力31.5 MPa;油液的密度为998 kg/m3,油液的体积弹性模量为1 980 MPa。
2 基于模糊理论的PID控制器
2.1 模糊PID设置
模糊PID控制系统框图如图5所示。

图5 模糊PID控制系统框图
在不破坏常规PID控制原则的前提下,模糊PID以平衡缸位移误差e和误差变化速率ec作为系统的输入,通过制定的模糊控制规则,自适应调整PID参数,以应对系统的不断变化,进一步提高对非线性系统的控制效果。
在控制过程中,模糊规则数目过多会导致算法过于复杂,以及运行速率下降,因此,一般将模糊子集数目取为3~9个[14]。
综合考虑支架平衡缸的实际工况,笔者将位移e和位移变化率ec离散化为7个等级,分别为:{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)};e的论域设为{-3、-2、-1、0、1、2、3},ec的论域设为{-6、-5、-4、-3、-2、-1、0、1、2、3、4、5、6};ΔKp、ΔKi、ΔKd的论域均设为{-3、-2、-1、0、1、2、3},模糊子集为{NB,NM,NS,ZO,PS,PM,PB}。并设置相应的模糊规则。
ΔKp模糊控制规则表如表1所示。

表1 ΔKp模糊控制规则表
根据确定的模糊规则,可得出模糊规则控制曲面如图6所示。
从图6中可以看出:模糊规则控制曲面较为平滑,说明模糊规则设置合理。
2.2 模糊PID控制器模型建立
在Simulink中建立模糊PID控制系统仿真模型,如图7所示。

图6 模糊规则控制曲面
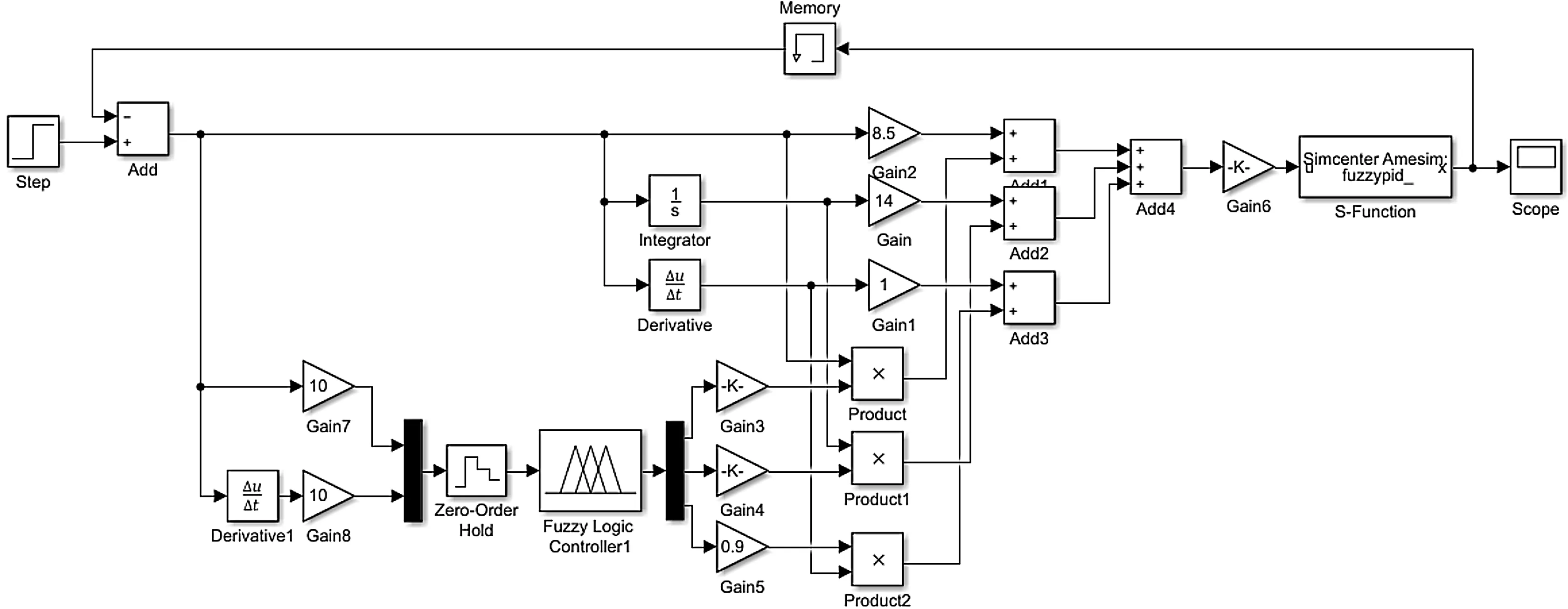
图7 模糊PID控制系统仿真模型
该模型利用S-Function模块实现了与AMESim模型信息的实时传输。
笔者通过试凑法得到了一组PID参数:Kp=8.5,Ki=14,Kd=1。
3 控制系统仿真效果分析
以给定的阶跃信号作为系统的输入,平衡缸的位移阶跃响应如图8所示。

图8 平衡缸位移阶跃响应
从图8中可以看出:常规PID平衡缸位移阶跃响应达到稳态的调节时间约为4.5 s,超调量为2.6 mm;引入模糊控制理论后,平衡缸位移阶跃响应达到稳态的调节时间缩短为2.3 s,超调量降低了1.2 mm。
由此可知,模糊自适应PID控制超调量较小,系统产生的振荡小,系统能够快速地趋于稳态。
为了测试该系统的自适应能力和动态稳定性,在系统达到稳态后,笔者以阶跃信号模拟基本顶断裂或坍塌时对支架的冲击力,在第8 s施加150 kN的外载荷。
冲击载荷下平衡缸位移阶跃响应如图9所示。

图9 冲击载荷下平衡缸位移阶跃响应
从图9中可以看出:采用模糊PID控制算法后,平衡缸对动载荷的响应较快,调节时间为2 s,超调量为0.56 mm,而常规PID调整平衡缸响应曲线响应波动较大,调节时间为5 s,超调量为0.78 mm。
综上所述,在支架平衡缸位置控制系统中,模糊PID在控制过程中能够自主调节PID参数,相比于常规PID具有更快的响应速度、更强的抗干扰能力、更小的超调量。
4 结束语
在分析了电液比例阀控缸工作原理的基础上,笔者建立了平衡缸位置控制系统的数学模型;并利用AMESim-Simulink联合仿真模型进行了仿真实验。
实验结果表明:与常规PID相比,模糊PID的响应时间更短,超调量更小,可在一定程度上提高系统应对时变和非线性的能力;而且在冲击载荷下,与常规PID相比,模糊PID控制器也表现出了更好的自适应性、鲁棒性和动态稳定性。
目前,与模糊理论相关的控制算法在各类控制系统已被不断应用,因此本文对液压支架控制系统以及其他非线性控制系统都具有一定的参考和应用价值。
