移动载体上电磁轴承-转子系统空间位置的动力学建模与分析*

吴妙妮，蒋科坚

(浙江理工大学 信息学院，浙江 杭州 310018)

0 引 言

在目前的转子系统动力学研究过程中，大多数的研究条件是将转子系统安装在载体的质心位置处[1]。但是在实际应用中，因不同的需求，转子系统可能没有安装在载体的质心位置处。

当载体运动时，转子系统在载体上的任意安装位置和轴向方向对其动力学特性存在的影响，是一个需要解决的问题。即当转子系统在载体上的安装位置和轴向方向发生变化时，研究其动力学特性的变化是有必要的。林富生等[2，3]将转子系统安装在移动载体的质心位置处，研究了载体匀速或匀变速运动对其转子系统动力学特性的影响，及载体的基础运动激励对转子运动特性的影响[4]，机动开始和结束条件下的转子系统动力学特性[5]和载体的大幅度运动与定子运动之间的关系[6]。LU Z Y等[7]使用有限元方法建立转子模型，研究了有限元降阶方法。

而在目前的动力学研究中，学者将转子系统安装载体的质心位置处、轴向方向与载体前进方向平行，研究了双转子系统的非线性响应特性[8]、耦合双转子系统的运动特性[9]、基础激励下的电磁轴承转子系统振动控制[10]、多频振动控制[11]、主动振动控制问题[12]等。在上述研究中的模型大多是基于转子系统的安装位置为载体的质心、轴向方向与载体的前进方向平行，考虑载体运动对其转子动力学特性的影响。当载体运动时，转子系统在载体不同位置条件下的动力学问题的研究较少，需进一步研究。

为了研究载体运动时转子系统的位置对其动力学特性的影响，笔者首先建立转子系统在移动载体任意位置条件下的运动微分方程；然后以一个单盘、多质量和单轴承的柔性转子系统为实验对象，在载体运动条件下，采用MATLAB/Simulink建模，研究转子系统安装位置和轴向方向的不同对其动力学特性的影响；最后，在一个电磁轴承转子系统上进行振动实验，以验证模型的正确性。

1 转子系统的运动方程

为了方便分析，笔者建立4个三维直角坐标系，分析转子系统在载体任意安装位置和轴向方向条件下的总动能；基于Lagrange方程，建立单盘、多质量和单轴承的柔性转子系统的一般运动微分方程。

1.1 坐标系建立

转子系统在移动载体上的安装位置有多种形式。一般为了减小转子系统安装位置和轴向方向对动力学特性的影响，将转子系统安装在载体的质心位置处。

带有单个转子系统的载体常用坐标名称和方向如图1所示。

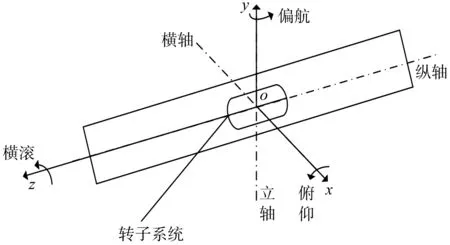
图1 转子系统在载体上的位置和坐标系

单个转子系统安装在载体的质心位置处，载体绕纵轴oz、横轴ox和立轴oy的转动称为横滚、俯仰和偏航。在实际应用过程中，转子系统在载体上的位置会根据不同的需求而安装在不同的位置上。假设转子系统在载体上的安装位置是任意的，轴向方向也是任意的。

为了方便描述转子系统在载体上的位置，笔者采用了地面固定直角坐标系OXYZ、载体相对直角坐标系oxyz、辅助直角坐标系o′σηζ和转子直角坐标系o′x′y′z′。

转子系统与坐标系OXYZ，oxyz，o′σηζ与o′x′y′z′之间的关系如图2所示。

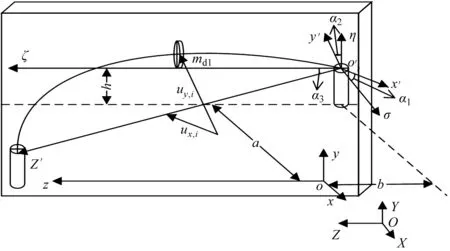
图2 转子与坐标系统示意图

笔者用位于地面上的固定直角坐标系OXYZ来描述载体的空间运动状态，主要是对载体的速度和加速度进行描述。

载体相对直角坐标系oxyz是以载体的质心o为坐标系原点，固定在载体表面上的直角坐标系，用来描述载体的转动运动。其轴与地面固定坐标系OXYZ各轴平行，方向一致。

辅助直角坐标系o′σηζ是为了方便描述转子系统在载体上角度变化的直角坐标系。辅助直角坐标系o′σηζ的各轴与载体相对直角坐标系oxyz对应轴之间存在安装位置参数a，b，h。

转子直角坐标系o′x′y′z′的各轴分别与辅助直角坐标系o′σηζ的对应轴存在轴向方向参数α1、α2、α3。

载体作为一个刚体，运动状态完全由地面固定坐标系OXYZ上的平动分量[XB,YB,ZB]和载体相对坐标系oxyz上的转动分量[θB,x,θB,y,θB,z]来描述。

1.2 转子系统的能量与广义力

基于文献[13]的研究，笔者在转子系统的任意安装位置基础上，进一步讨论转子系统安装位置和轴向方向都是任意的情况。

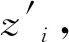
圆盘的动能Ti为：

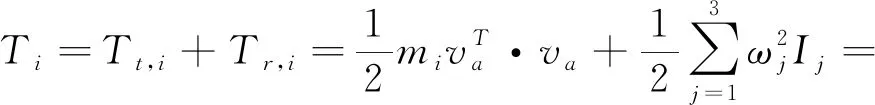
(1)

在大多数研究中，将转子系统安装在载体的质心位置处，此时相对位移矢量为:

(2)

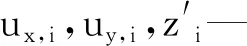
本文的研究是将转子系统安装在移动载体的任意安装位置和轴向方向上。因此，圆盘中心在载体相对直角坐标系oxyz的相对位移矢量r发生了变化，此时有：

(3)

式中：xp，yp—圆盘形心与质心在x，y轴上的关系，

则圆盘动能的平动部分Tt,i可表示为:

(4)

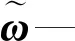
假设sin(θy,i+θB,y)≈θy,i+θB,y，cos(θy,i+θB,y)≈1，sin2β≈sin2α2和cos2β≈cos2α2，忽略其他高阶小量的影响，圆盘的角速度可以用载体的角位移[θB,x,θB,y]、转子直角坐标系o′x′y′z′与辅助直角坐标系o′σηζ的夹角[α1,α2,α3]和柔性轴相对于载体相对直角坐标系oxyz的转动角来表示，则有:

φ=θx+α1+θB,x；β=θy+α2+θB,y；γ=Ωt+α3

(5)

式中：φ,β,γ—盘在oxyz坐标系中x，y，z轴的角速度ωj。

则盘动能的转动部分Tr,i为:

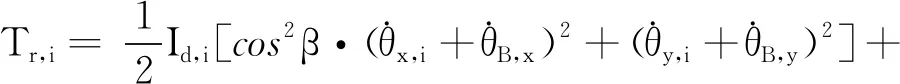
(6)

式中：Id,i，Ip,i—圆盘的直径，极转动惯量。

因此，盘的总动能为:

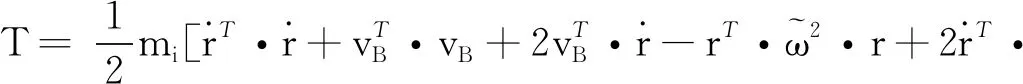
(7)

由于转子直角坐标系o′x′y′z′以转子的静变形为原点，轴的初始弹性恢复力与转子的重力之间形成了平衡关系，则在圆盘处的柔性轴弹性势能为:

(8)

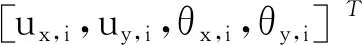
Ki的表达式为：

(9)

式中：klm—圆盘处于轴上的ux,i，uy,i，θx,i及θy,i方向的刚度系数，其中l，m分别为1，2，3，4。

如果圆盘上的阻尼是速度的线性函数，则圆盘上的耗散能为:

(10)

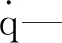
Ci的表达式为：

(11)

式中：ct,i，cr,i—盘的平动，转动阻尼系数。

假设FG,i为圆盘上的广义力,，则系统的广义力Q为

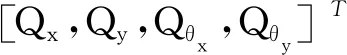
(12)

式中：fG,l(l为1，2，3，4)—在ux,i，uy,i，θx,i及θy,i方向上的非线性广义力。

1.3 转子系统的运动微分方程

对于非保守的系统，Lagrange方程[14]为:

(13)

式中：L—系统的Lagrange函数，L=T-V；T，V—系统的动能和势能；qj—盘的广义坐标；D—系统的耗散能；Qj—系统在qj自由度方向上所受的广义力。

将T，V，D和Q代入式(13)后，可得到圆盘在载体任意安装位置和轴向方向条件下的运动微分方程为:

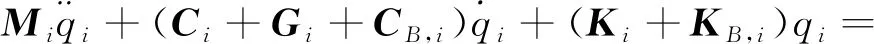
(14)

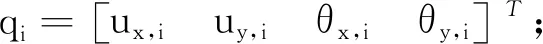
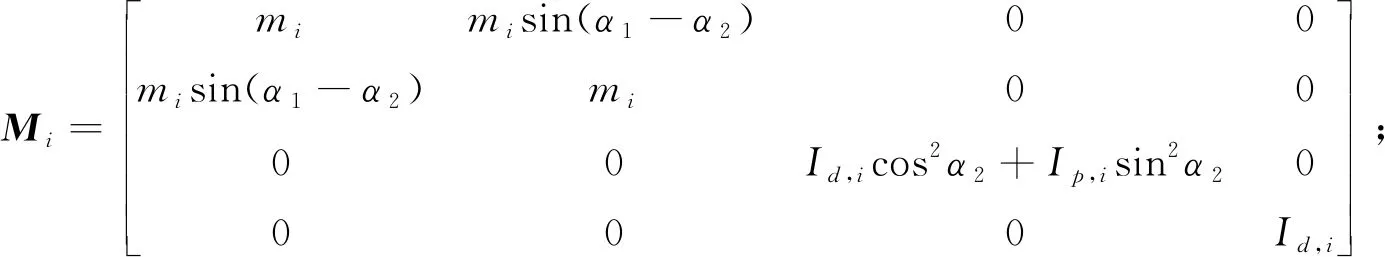
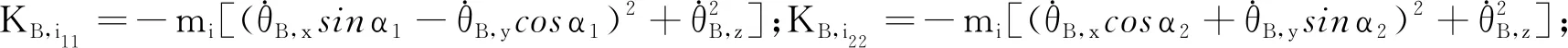
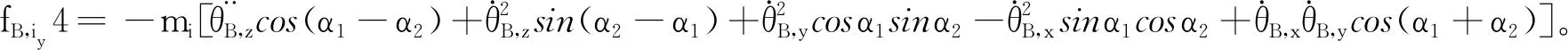
对于轴承上的集中质量，设质量中心相对于转子直角坐标系o′x′y′z′的广义坐标qi=[ux,i,uy,i]T(i=2,3)，对式(14)进行化简，可得到转子系统在载体上任意安装位置和轴向方向时，轴上某集中质量的运动微分方程为：

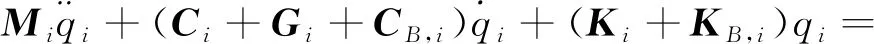
(15)

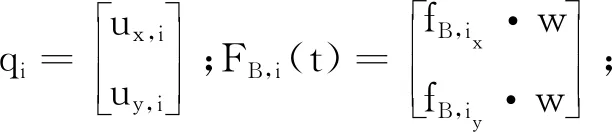
容易得到转子系统在移动载体任意安装装位置和轴向方向条件下，单盘、多质量和单轴承的柔性转子系统运动微分程为：

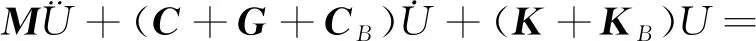
(16)

式中：M，G，C，K—转子系统的质量，陀螺，阻尼，刚度矩阵；Fu(t)，FG(t)—转子系统的不平衡力矢量，广义力矢量；Mn，Cn，Gn—圆盘或第n个集中质量(n=1，2，3)的质量，阻尼，陀螺矩阵；Fu,n(t)，FG,n(t)—圆盘或第n个集中质量上的不平衡力矢量，广义力矢量；CB，KB，FB(t)—转子系统在移动载体任意安装位置和轴向方向条件下的附加阻尼效应矩阵，附加刚度效应矩阵，附加外激励力矢量；CB,n，KB,n，FB,n—转子系统在载体上的安装位置和轴向方向任意时，圆盘或第n个集中质量上产生的附加阻尼效应矩阵，附加刚度效应矩阵，附加外激励力矢量。

其中：U=[q1…qn]T；

2 空间位置对转子系统动力特性的影响

将转子系统在载体任意位置条件下的运动方程与文献[15]中的转子系统，在载体质心条件下的运动方程进行对比，可以得到：

当载体在做匀速平动运动时，安装位置参数a，b，h只影响附加外激励力，但此时的转子系统无附加外激励力产生，所以转子系统的安装位置参数对其运动特性没有影响。虽然轴向方向参数α1,α2,α3对转子系统存在多方面的影响，但载体在做匀速平动运动时，轴向方向参数对转子运动特性没有影响。

当载体在做匀速转动运动时，转子系统的安装位置参数a，b，h影响附加外激励力的大小。因此，当载体在做匀速转动运动时，转子系统在载体上的安装位置不同会影响转子系统的运动特性。

当载体在做匀速转动运动时，转子系统在载体上的轴向方向参数α1、α2、α3对运动特性的影响较大。垂直于载体前进方向的平面xoy夹角α1和α2不仅对转子系统的惯性力、不平衡力产生影响，还对其附加刚度效应项、附加阻尼效应项、附加外激励力产生影响。而与载体前进方向纵轴的夹角α3，只对转子系统的附加外激励力产生影响。

所以，当载体在做匀速转动运动时，转子系统的轴向方向对运动特性存在影响。当轴向方向参数α1=α2=α3=0°时，转子系统的轴向方向对其动力学特性的影响最小。

3 仿真及结果分析

为了研究转子系统在载体上的安装位置和轴向方向不同对其动力学特性的影响，需要进行仿真分析。

笔者所研究的转子系统的简化模型如图3所示。

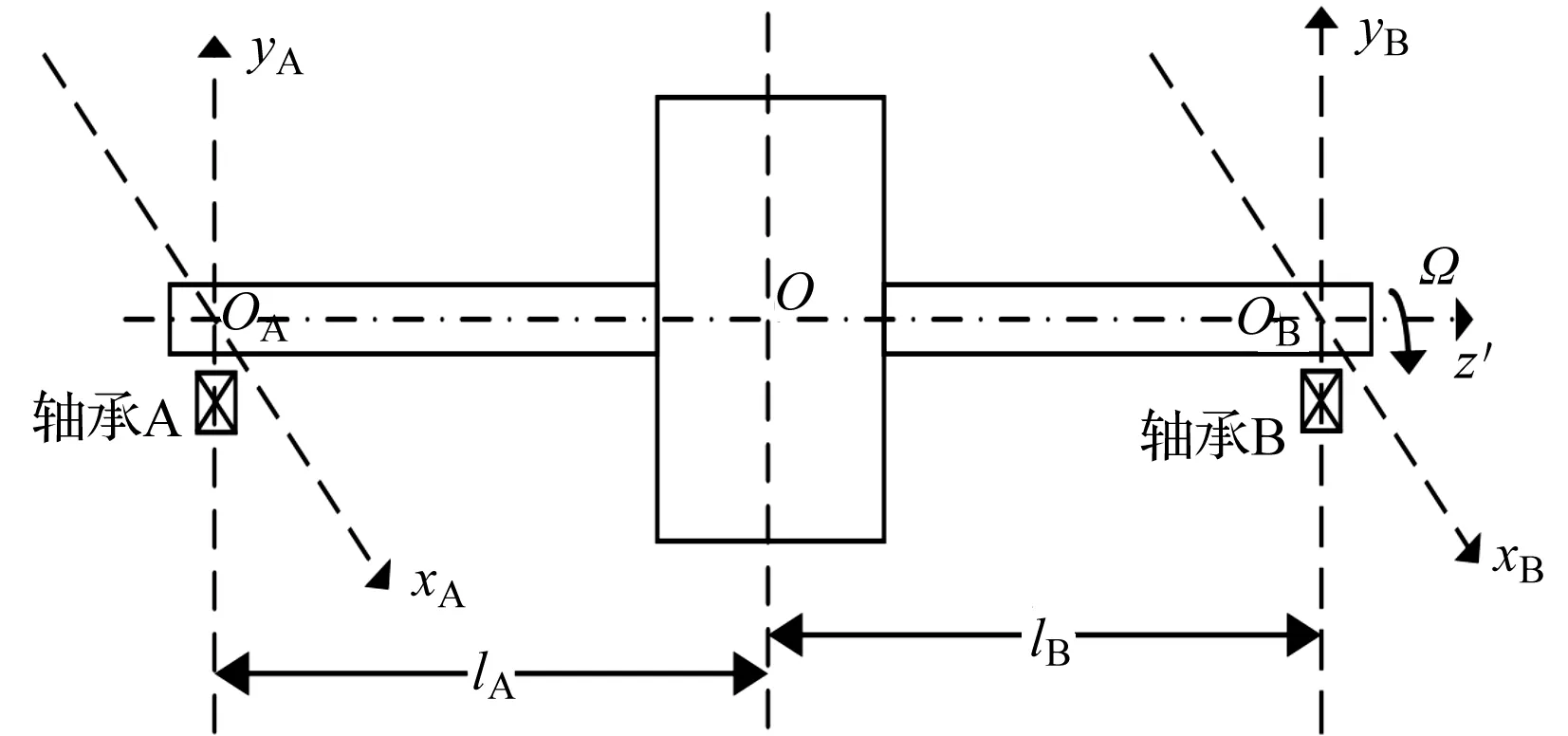
图3 柔性转子系统简化模型

该转子系统被简化为带有1个刚性圆盘、2个集中质量和1个无质量弹性轴，具有8个自由度。转子的基本参数分别为：无质量柔性轴的半径为0.03 m；lA=0.412 m；lB=0.373 m；l=lA+lB；圆盘的偏心距为0.1 mm；转子圆盘质量为50.3 kg；弹性轴承的集中质量为2 kg，转子稳定工作转速为5 000 r/min，载体的运动速度为200 m/s。在工作转速条件下，电磁轴承电流刚度系数为1 205i0N/A，电磁轴承位移刚度系数为3.7×106i02N/m。o点为转子系统的几何中心。

利用本文的推导，可以写出该转子系统在载体上的不同安装位置和轴向方向条件下的一般运动微分方程为：

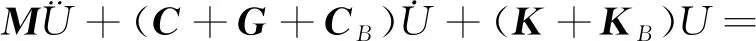
(17)

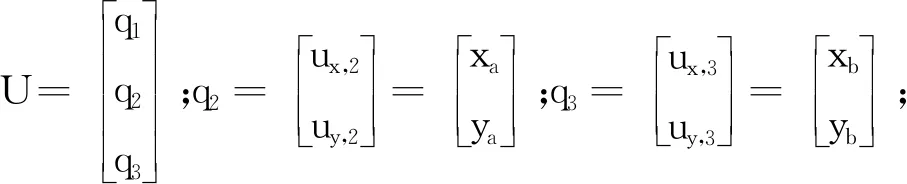
刚性圆盘的广义位移q1=[ux,1,uy,1,θx,1,θy,1]T，到轴承两端的位移为：

(18)

由于本文主要研究转子系统在移动载体上的位置参数对其动力学特性的影响，转子系统的安装位置描述如表1所示。

表1 转子系统安装位置

安装位置发生变化时，转子系统的轴向方向与载体纵轴oz平行：(1)当安装位置在载体相对直角坐标系oxyz原点上时，设转子系统安装移动载体的质心位置处；(2)当安装位置在坐标系oxyz的x轴上时，设转子系统安装移动载体的横轴上；(3)当安装位置在坐标系oxyz的z轴上时，设转子系统安装移动载体的纵轴上；(4)当安装位置在坐标系oxyz的y轴上时，设转子系统安装移动载体的立轴上。

转子系统的轴向方向描述如表2所示。

表2 转子系统轴向方向

轴向方向发生变化时，转子系统的安装位置在载体的质心位置处：(1)当轴向方向与坐标系oxyz的z轴平行时，转子系统的轴向方向与载体前进方向垂直的纵轴平行；(2)当轴向方向与坐标系oxyz的x轴平行时，转子系统的轴向方向与载体前进方向垂直的横轴平行；(3)当轴向方向与坐标系oxyz的y轴平行时，转子系统的轴向方向与载体前进方向垂直的立轴平行。

3.1 匀速平动运动

当载体在做匀速平动运动时，转子系统的稳态运动轨迹如图4所示。

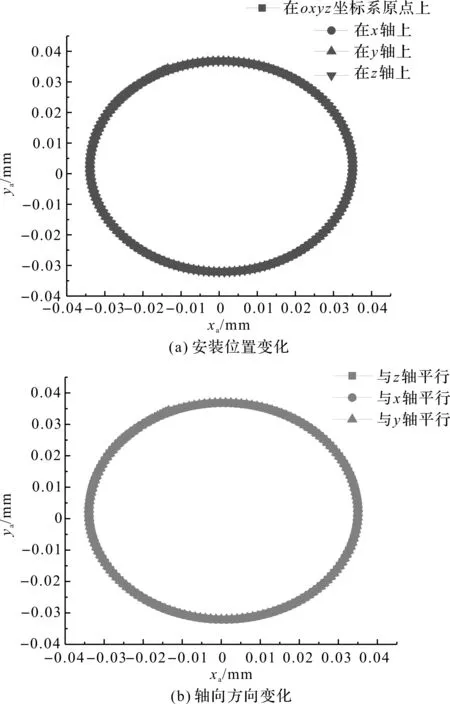
图4 匀速平动时转子运动轨迹

转子系统的稳态运动轨迹是以(x,y)=(0,0)为中心的圆。因为轴承A端与B端的运动轨迹是相对的，轨迹图以A端为例。当转子系统在载体上的安装位置变化、轴向方向不变时，转子系统的运动轨迹不变，因为转子系统中没有产生受安装位置参数影响的附加外激励力。当转子系统在载体上的安装位置不变、轴向方向变化时，转子系统的运动轨迹没发生变化。

因此可得到结论：即当载体在做匀变速平动运动时，转子系统在载体上的安装位置和轴向方向可以任意。

3.2 匀速转动运动

当载体在做匀速转动运动时，转子系统的稳态运动轨迹如图5所示。

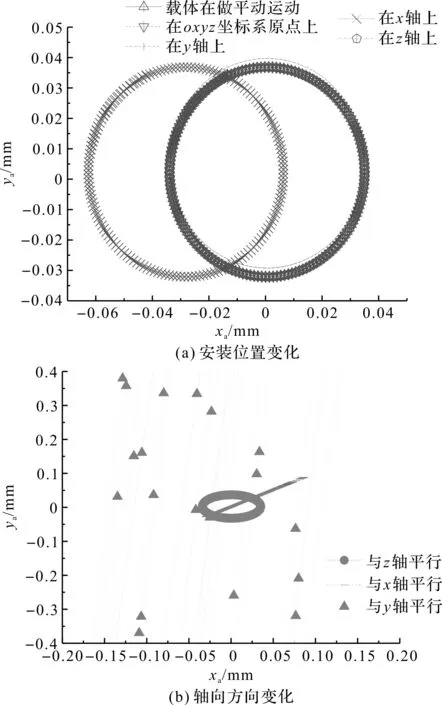
图5 匀速转动时转子运动轨迹

由图5可知：匀速转动时转子系统的稳态运动会发生变化：(1)转子系统安装在x轴时，运动轨迹中心向在x轴负方向发生偏移；(2)转子系统安装在y轴时，运动轨迹中心向y轴正方向偏移；(3)转子系统安装在z轴时，运动轨迹是以(x,y)=(0,0)为中心的圆；

转子系统的轴向方向变化情况为：(1)转子系统的轴向方向与y轴平行时，转子系统的运动轨迹不是稳定状态；(2)转子系统的轴向方向与x轴平行时，转子系统的运动轨迹是一条过(x,y)=(0,0)直线；(3)转子系统的轴向方向与z轴平行时，转子系统的运动轨迹是以(x,y)=(0,0)为中心的圆。

当轴向方向参数全为0°，即转子系统的轴向方向与载体前进方向平行时，安装参数变化情况如下：

(1)当安装位置参数a发生变化，即转子系统安装在与载体前进方向垂直的横轴任意位置时，转子系统的运动轨迹大小没发生变化。但是由于在x轴方向产生了一个恒定的附加外激励力，导致转子轨迹中心在x轴方向发生了偏移；

(2)当安装位置参数b发生变化，即转子系统安装在载体前进方向纵轴上的任意位置时，转子运动轨迹大小没发生变化。因为没有产生附加外激励力，转子轨迹的中心也没发生偏移；

(3)当安装位置参数h发生变化，即转子系统安装在与载体前进方向垂直的立轴任意位置时，转子系统的运动轨迹大小没发生变化。但是由于在y轴方向产生了一个恒定的附加外激励力，转子的运动轨迹中心在y轴方向发生偏移。

因此，当载体在做匀速转动运动时，转子系统的轴向方向相同、安装位置参数a、h的变化对运动特性的影响较大，安装位置参数b的不同对运动特性的影响较小。

所以可以得到另一结论：即当载体在做匀速转动运动，且转子系统在载体上的位置没有明确要求时，转子系统的安装位置在载体前进方向纵轴上可以任意，但在与载体前进方向垂直的轴上不能任意。

当安装位置参数全为0 m，即转子系统的安装位置在质心处时，轴向方向的变化情况如下：

(1)当转子系统的轴向方向与载体前进方向垂直的横轴平行时，因为轴向方向参数α1、α3的存在，转子系统的惯性力、附加阻尼效应项、附加刚度效应项和附加外激励力发生了变化，导致转子系统运动轨迹中心在x轴方向发生偏移，大小发生变化；

(2)当转子系统的轴向方向与载体前进方向垂直的立轴平行时，转子系统不能稳定运行，产生碰撞。这是因为轴向方向参数α2、α3的存在，不仅影响转子系统的惯性力、附加刚度效应项和附加外激励力，而且影响转子系统的陀螺效应项。

因此，当载体在做匀速转动运动时，不能忽略转子系统的轴向方向不同对其运动特性的影响。

所以可以得到结论：即当载体在做匀速转动运动，且转子系统在载体上的位置没有特殊要求时，转子系统的轴向方向参数不能为任意值，即转子系统的轴向方向不能任意；并且转子系统的轴向方向应尽可能不与载体前进方向垂直的立轴平行。

3.3 振动仿真

当转子系统的安装位置在载体的质心位置处、轴向方向与载体的前进方向纵轴平行时，转子在静止状态下，笔者基于Lagrange方程模型进行了载体静止或载体在Y方向以一个正弦信号作振动运动时的仿真实验。

转子系统的振动仿真轨迹图如图6所示。

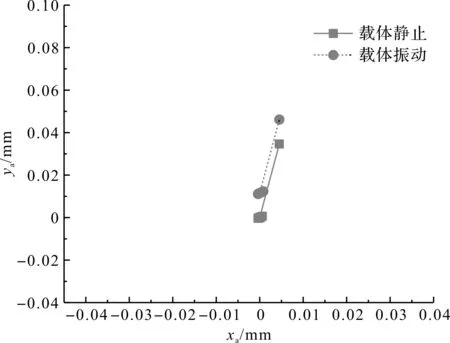
图6 转子系统的振动仿真轨迹图

载体静止时的转子运动轨迹图在载体的Y方向以一个正弦信号作振动运动时的转子轨迹图之下。当载体在Y方向以一正弦信号作振动运动时，在y轴方向产生一个附加的外激励力，导致转子的轨迹中心在y轴方向发生偏移。所以当载体在做振动运动时，会导致转子与定子之间产生局部碰撞。

4 实验研究

4.1 实验平台

为了验证仿真模型，笔者在电磁轴承-转子系统半实物仿真平台上进行了实验。实验振动平台如图7所示。

图7 电磁轴承转子系统振动平台

电磁轴承安装在一块由6个弹簧脚垫支撑的钢板上，钢板的一边安装了振动电机。此时的转子系统安装在载体的质心位置处，轴向方向与载体前进方向纵轴平行。转子悬浮控制器由4个自由度的PID控制，系统的采样频率为10 kHz。转子质量为m=9.92 kg，轴承气隙为0.5 mm。振动电机的振动频率设置为50 Hz。

4.2 实验及结果分析

载体静止即振动电机没有运动时，笔者检测到电磁轴承转子静止状态下的转子运动轨迹图，如图8所示。

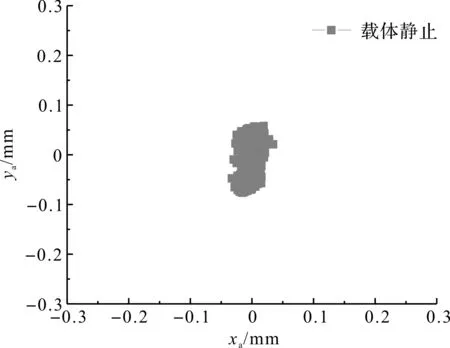
图8 静止时转子系统的轨迹图

当载体静止时，转子系统的运动轨迹图相对收敛。

振动电机运动即载体在Y轴以一正弦信号振动时，笔者检测到电磁轴承转子系统静止状态下的转子相对运动轨迹图，如图9所示。

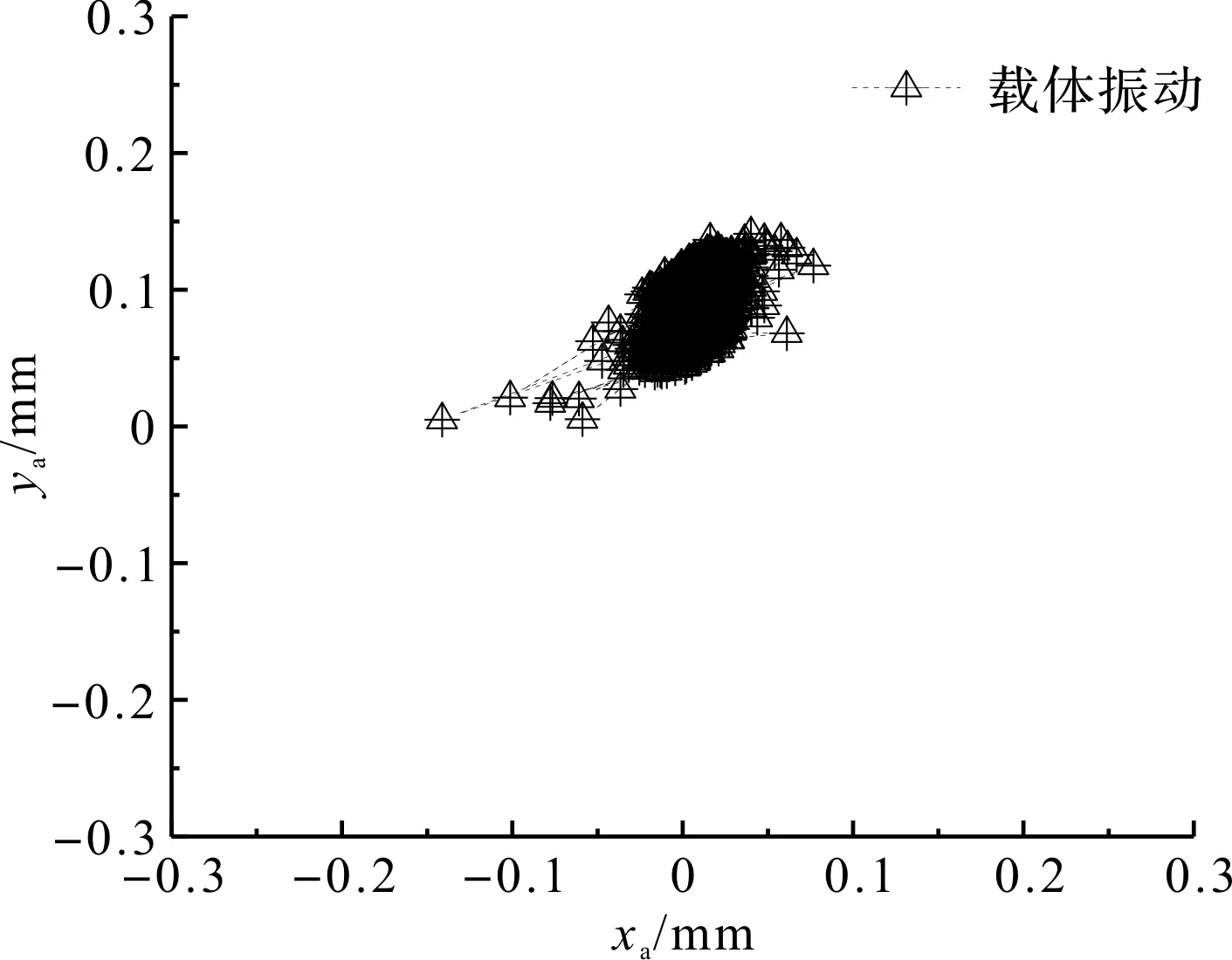
图9 正弦振动时转子系统的轨迹图

图9中，当载体正弦振动运动时，转子系统的轨迹图相对发散；并且将载体振动条件下转子系统的运动轨迹中心与载体静止条件下的运动轨迹中心进行对比可知，其轨迹中心在y轴方向发生了偏移；对比分析相同条件下的仿真模型结果可知，运动轨迹中心偏移趋势相同。但是由于振动电机和外界环境的干扰，实验平台中的转子运动轨迹大小会与仿真模型的结果不一致。

5 结束语

为了研究当载体运动时，转子系统的位置对其动力学特性的影响，笔者建立了转子系统在移动载体上的任意安装位置和轴向方向模型，研究了转子系统安装位置和轴向方向不同对其动力学特性的影响；然后，在一个电磁轴承转子系统上进行振动实验，并将结果与仿真结果进行对比，验证了模型的正确性。

研究结果表明：当载体在空间内运动且对转子系统的位置没有明确要求时，为了减小转子系统的安装位置和轴向方向不同对其运动特性的影响，转子系统的安装位置可以在载体纵轴线上的任意位置处，即安装位置参数a=h=0 m，轴向方向与载体前进方向纵轴平行，即轴向方向参数α1=α2=α3=0°。该结果为转子系统在移动载体上的位置安装提供了理论依据。

因实验条件有限，在下一研究阶段，笔者将通过进一步搭建半实物仿真系统平台，验证转子系统在移动载体上的位置对其动力学特性的影响。