具有基座松动和碰摩故障的拉杆转子-轴承系统动力学分析*
2020-12-24郑美茹
郑美茹,黑 棣
(1.陕西铁路工程职业技术学院 机电系,陕西 渭南 714000;2.三门峡速达交通节能科技股份有限公司,河南 三门峡 472000)
0 引 言
转子-轴承系统是动力设备的核心部件,其运行稳定性直接决定了动力设备的运行稳定性和安全性。如果转子系统出现故障,则会导致整个设备无法正常运转,甚至出现重大的事故。
轴承基座松动和碰摩耦合故障是转子-轴承系统最常见的故障之一。因此,针对此类故障开展研究,分析其动力特性,掌握其产生机理,有利于对转子故障进行诊断。
许多学者针对转子的基座松动、转子与机匣碰摩故障进行研究。蒋勉[1]考虑了轴承基座松动,并在此基础上建立了轴承-转子系统动力学模型,通过计算建立了轴承-转子系统非线性度与松动程度之间的关系,进而形成了一种支承松动的评估方法;王威[2]建立了有界噪声激励作用下的碰摩转子模型,并运用替代算法分析了受不确定性激励碰摩转子的响应;刘杰[3]建立了转轴和轮盘松动的转子系统模型,并且研究了非稳态油膜力对该松动系统动力学行为的影响,并通过实验进行了验证;TIAN G[4]通过实验研究了飞机机体侧倾飞行时具有碰摩故障的转子的动力学行为,通过频谱图、小波比例尺等方法获得了碰摩转子的一些新特征;BAB S[5]根据燃气轮机建立了转子-轴承系统模型,并且研究了光滑非线性能量池对转子运动的影响;通过遗传算法分析可知,光滑非线性能量池可以有效地减小振动和碰摩现象,同时可以使转子运行更加平滑;刘杨[6]考虑了轴承基座松动-碰摩耦合故障,并建立了转子-轴承系统模型,同时将故障转子与健康转子的动力学特性进行了比较验证,从而为具有该故障的转子诊断提供了理论依据;蒋勉[7]针对具有支承松动-碰摩耦合故障的转子进行了分析,通过计算建立了轴承-转子系统非线性度与松动程度之间的关系,进而形成了一种支承松动的评估方法。
以上研究主要是针对整体转子的支座松动、碰摩故障进行的研究,而且取得了非常多的成果。拉杆转子在动力设备中也得到了广泛的应用,因此,一些学者针对具有故障的拉杆转子也进行了深入研究。胡亮[8,9]利用达朗贝尔原理建立了拉杆转子模型,分别分析了定点碰摩拉杆转子和带横向裂纹拉杆转子的动力学行为;姚康瑞[10]基于达朗贝尔原理建立了拉杆转子模型,分析了健康转子和具有碰摩故障转子的动力学行为。
笔者建立周向拉杆转子模型,同时考虑转子一端轴承支座松动和轮盘与定子之间的碰摩故障,基于有限长滑动轴承油膜力近似解析解,运用Newmark法分析同时具有这两种故障的拉杆转子动力学行为。
1 转子系统模型
笔者考虑了转子的基础松动和碰摩故障,转子模型采用拉杆转子模型,如图1所示。

图1 考虑基础松动和碰摩的拉杆转子-轴承系统示意图A(B)-转子的左右两端(即滑动轴承支撑处);O1(O2)-两个轮盘的几何中心;K1(K2)-轴段AO1(BO2)的抗弯刚度(在本文中取K1=K2);Fx(Fy)-滑动轴承油膜力沿x(y)轴负方向的分量;Kpm-轮盘O1与定子的碰摩刚度;Ks-基座的松动刚度;ms-基座的松动质量;δ-轮盘O1与定子间的间隙
图1中,两轮盘O1和O2依靠拉杆螺栓将它们紧紧地压在一起(本文将拉杆等效为具有非线性刚度的弹簧,其回复力可写为Fr=KbT+KrT3。
其中:Kb-拉杆弯曲刚度;Kr-拉杆非线性刚度;T-两轮盘相对位移。
假设轴段AO1的质量集中于A端轴承处,等效质量为mA;轴段BO2的质量集中于B端轴承处,等效质量为mB;两轴段均等效为无质量的弹性轴。两轮盘的质量分别为mO1和mO2。
1.1 滑动轴承油膜力的求解
此处滑动轴承采用有限长滑动轴承模型,笔者运用分离变量法和变分原理求解了Reynolds方程,并得到了油膜力的近似解析解[11]。
无量纲油膜压力分布函数P(φ,λ)的表达式为:
P(φ,λ)=P*(φ)ζ(λ)
(1)
式中:λ-滑动轴承轴向坐标;φ-滑动轴承周向坐标;P*(φ)-周向压力分布函数;ζ(λ)-轴向压力分布函数。
ζ(λ)表达式为:
(2)
式中:L-轴承宽度;d-轴承直径;W,V-中间变量。
W、V的表达式如下:
(3)

其中:
(4)
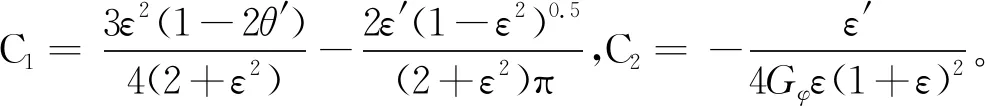
滑动轴承的无量纲油膜力可通过下式求得:
(5)
(6)
式中:Fr(Ft)-油膜力在径向(切向)的分量;Fx(Fy)-油膜力在x(y)方向的分量。
1.2 碰摩力模型
轮盘O1与定子的碰撞模型如图2所示。

图2 轮盘与定子的碰撞模型Fpn-轮盘O1与定子碰撞的法向力;Fpt-轮盘O1与定子碰撞的切向力
图2中,定子与轮盘间的间隙为δ,摩擦系数为γ,则碰摩力可写为:
(7)
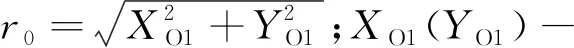
将碰摩力转化到x和y方向上,可写为:
(8)
1.3 具有碰摩和基座松动拉杆转子动力学方程
针对图1所示的拉杆转子无量纲动力学方程,可写为如下形式:
(9)
式中:M-无量纲质量矩阵;K-无量纲刚度矩阵;F-无量纲油膜力列向量;Q-无量纲外激励力列向量;W-无量纲重力列向量;FR-无量纲非线性回复力列向量;Fpm-轮盘O1与定子的碰摩力列向量;q-无量纲转子位移列向量。
其中,
q=[XA,YA,XO1,YO1,XO2,YO2,XB,YB,Ys]T,
F=[-FxA,-FyA,0,0,0,0,-FxB,-FyB,FyA]T,
W=[0,mA,0,mO1,0,mO2,0,mB,ms]T,
FR=[0,0,Kr(XO2-XO1)3,Kr(YO2-YO1)3,-Kr(XO2-XO1)3,-Kr(YO2-YO1)3,0,0,0]T,
Fpm=[0,0,kpm(1-δ/r0)(-XO1+γYO1),kpm(1-δ/r0)(-YO1-γXO1),0,0,0,0]T,
M=
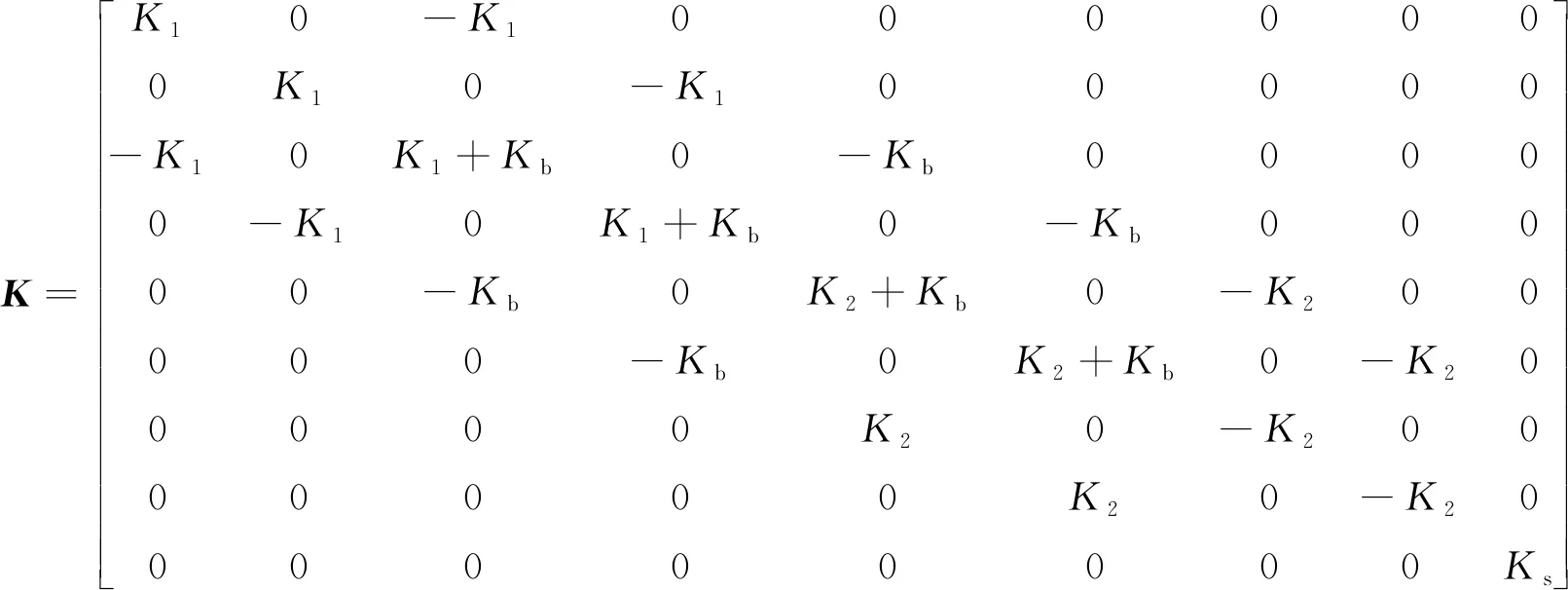

基座松动刚度Ks可写为:
(10)
式中:χ-松动间隙。
此处令Ks1=Ks3,Ks2=0。
2 数值算例及结果分析
笔者根据上述基础松动和碰摩的拉杆转子模型,采用Newmark数值积分法分析转子的动力学响应,计算时均采用无量纲量。
转子系统的参数如下:

首先,笔者将4种情况下(不考虑碰摩和基座松动、仅考虑碰摩、仅考虑松动和同时考虑碰摩与基座松动)转子的运动行为进行了比较,如图3所示。

图3 4种情况下转子的分岔图及时转子左端轴承处轨迹比较
图3(a~d)给出了4种情况下转子左端轴承处的分岔图:

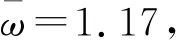
由以上分析可知:(1)拉杆转子无故障时,其分岔点最小,同时具有碰摩和基座松动故障转子的分岔点介于仅有碰摩故障和仅有基座松动故障转子的分岔点之间;(2)存在故障的转子,可以研究的转速范围更广,而且转子的运动行为更丰富复杂;(3)从分岔图可以看出,基座松动对转子运动的影响更大一些。
接着,笔者分别以转子的无量纲转速、松动刚度以及拉杆刚度为控制参数,研究了具有碰摩和基座松动故障拉杆转子的动力学行为。
2.1 无量纲转速对转子系统动力学的影响
本节以无量纲转速为控制参数分析转子系统的动力学行为。
转子松动端、轮盘O1、松动质量块的分岔图如图4所示。
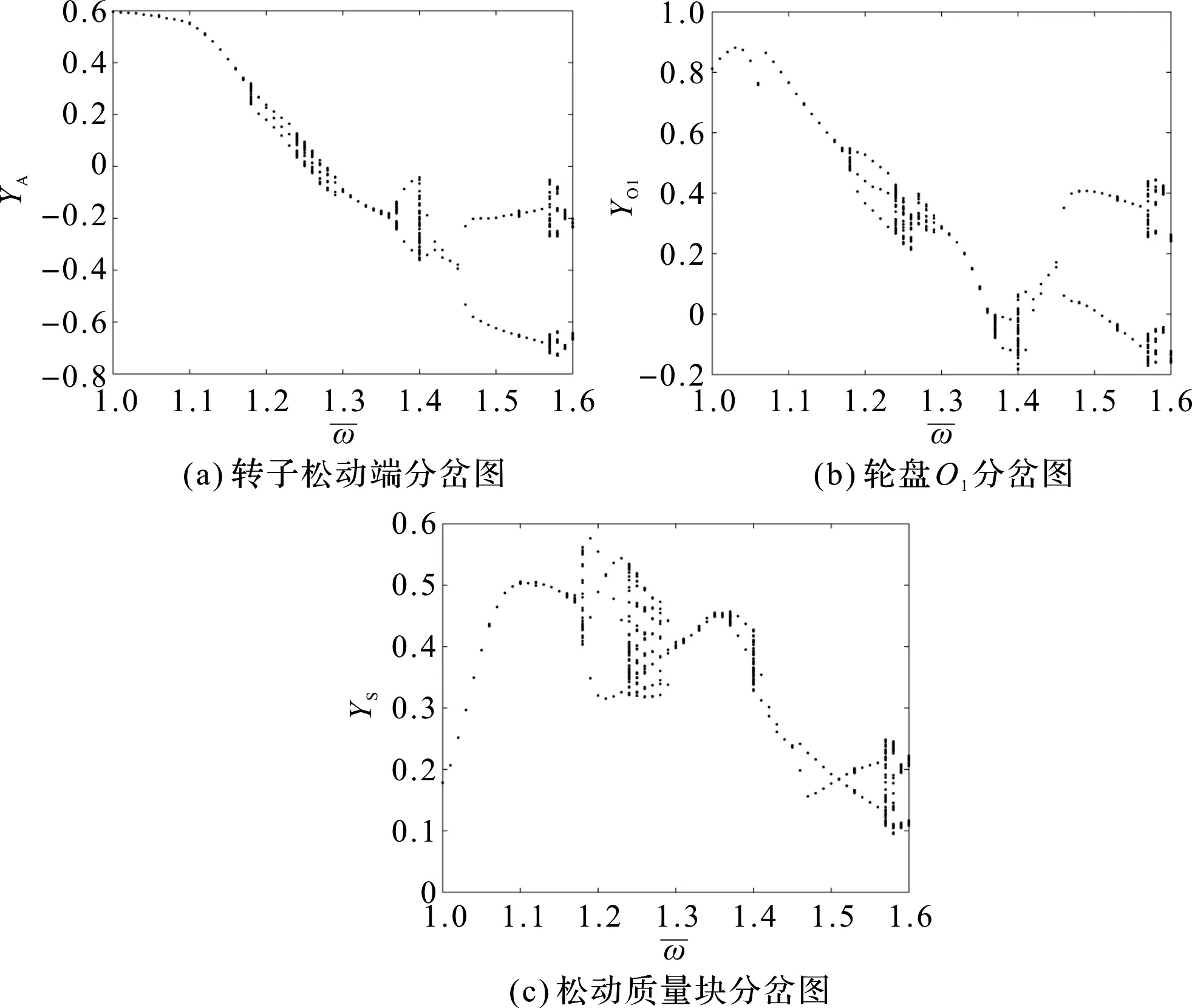
图4 转子系统随转速变化的分岔图
图4中,无量纲转速范围为1~1.6;松动质量块有着与转子相同的运动行为。
随转速变化转子的运动变化规律如图5所示。
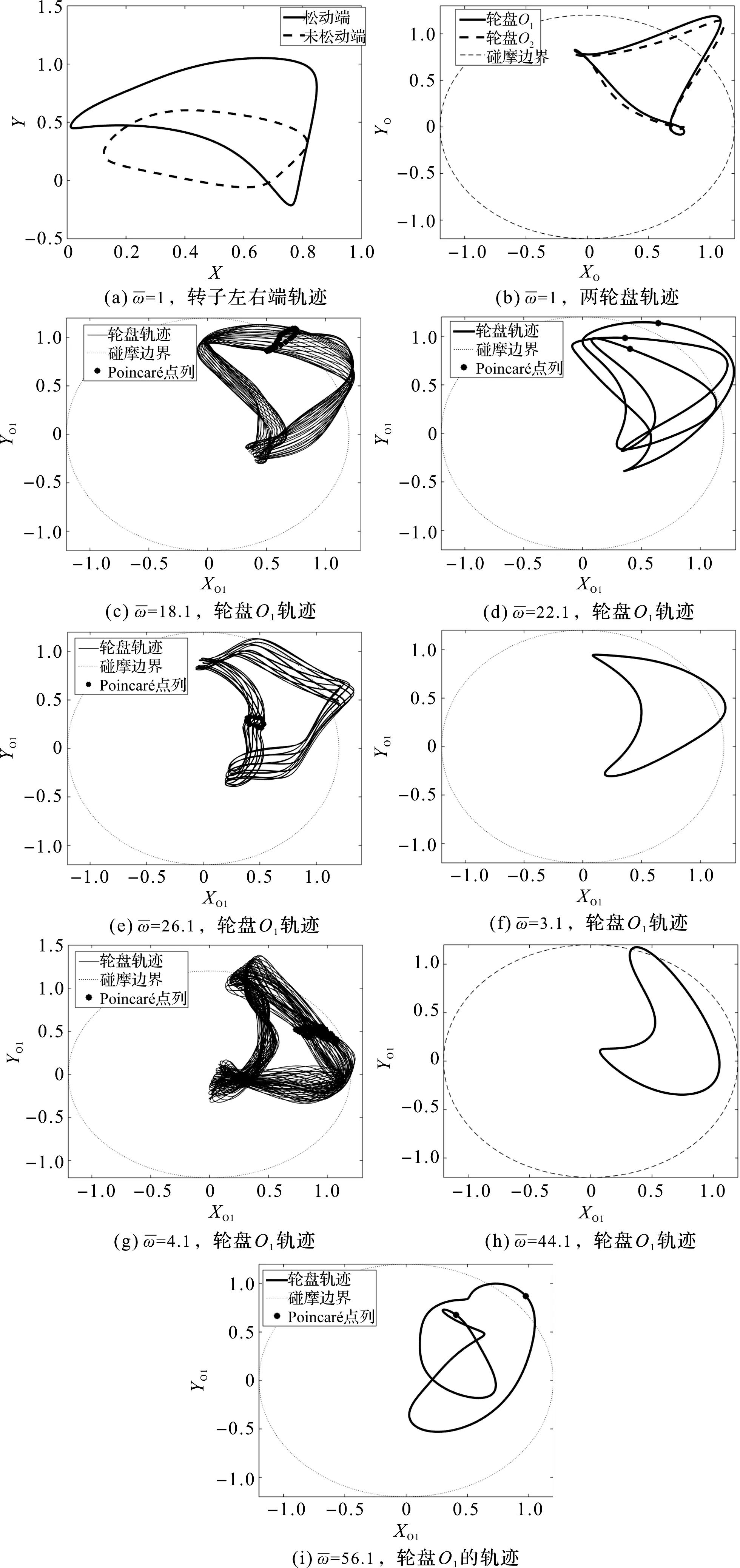
图5 不同转速下转子的运动轨迹
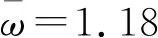
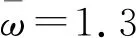
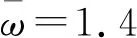
2.2 无量纲松动刚度对转子系统动力学的影响
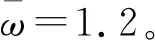
转子松动端和轮盘O1随松动刚度变化的分岔图如图6所示。
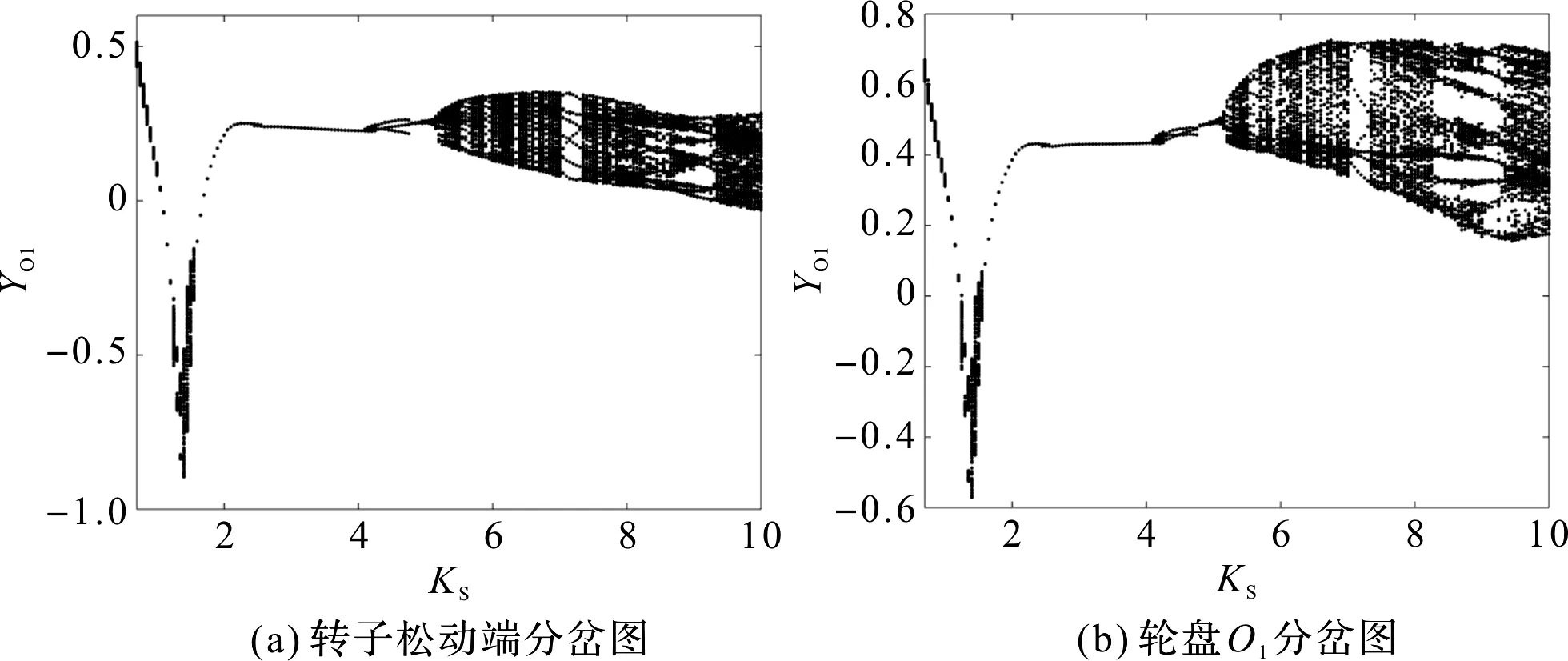
图6 转子系统随松动刚度变化的分岔图
从图6中可以看出,随着松动端刚度的变化,转子的运动行为变化非常丰富,所以松动刚度对转子的运动有很大影响。
随着松动端松动刚度的变化,转子轮盘O1处的运动变化规律如图7所示。
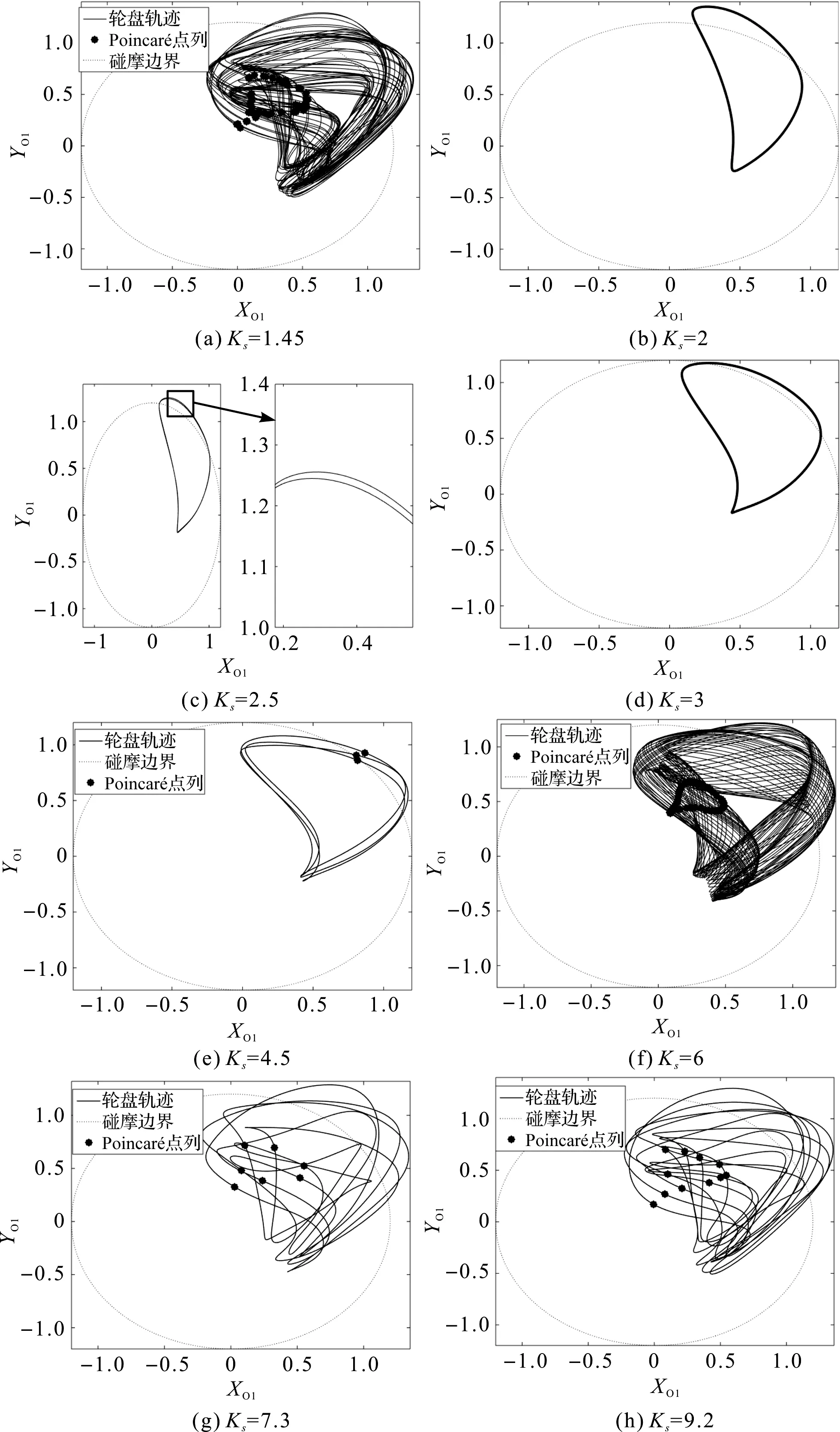
图7 不同松动刚度下的轮盘O1的运动轨迹
当松动刚度较小时,转子的运动为准周期运动,当Ks=1.45时,图7(a)给出了轮盘O1的运动轨迹和Poincaré映射,图中显示轮盘O1的运动轨迹限定与一个特定的区域,且Poincaré点列为一近似于圆的封闭曲线,故此时处于准周期运动。随着松动刚度增加,转子将倒分岔为周期运动。当Ks=2时,图7(b)给出了轮盘O1的周期运动轨迹。随着松动刚度的增加,转子出现了短暂的倍周期运动,当Ks=2.5时,图7(c)给出了转子轮盘O1处倍周期运动轨迹。
随着松动刚度的继续增加,转子将由倍周期运动倒分岔为周期运动。当Ks=3时,图7(d)给出了转子轮盘O1处周期运动轨迹。在周期运动之后,转子又变为周期三运动,当Ks=4.5时,图7(e)给出了转子轮盘O1处周期三运动轨迹及Poincaré映射。松动刚度继续增加,转子由周期三运动变为准周期运动,当Ks=6时,图7(f)给出了转子轮盘O1处准周期运动轨迹及Poincaré映射。在准周期运动阶段还包含了其它多周期运动。当Ks=7.3时,图7(g)给出了转子轮盘O1的轨迹和Poincaré映射。由图7(g)可以看出,转子的轨迹是7条封闭的曲线,并且在Poincaré截面上留下7个独立的点,所以此时转子系统处于周期七运动。当Ks=9.2时,图7(h)给出了转子轮盘O1的轨迹和Poincaré映射。由图7(h)看出,转子的轨迹是11条封闭的曲线,且Poincaré点列为11个独立的点,故此时转子处于周期十一运动。
2.3 无量纲拉杆刚度对转子系统动力学的影响

转子松动端和轮盘O1处转子运动随拉杆刚度变化的分岔图如图8所示。
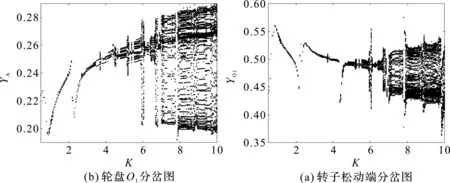
图8 转子系统随拉杆刚度变化的分岔图
由图8可知,在拉杆刚度变化时,转子的运动也呈现出较为复杂丰富的运动行为。
随着拉杆刚度的变化,转子运动的变化规律如图9所示。
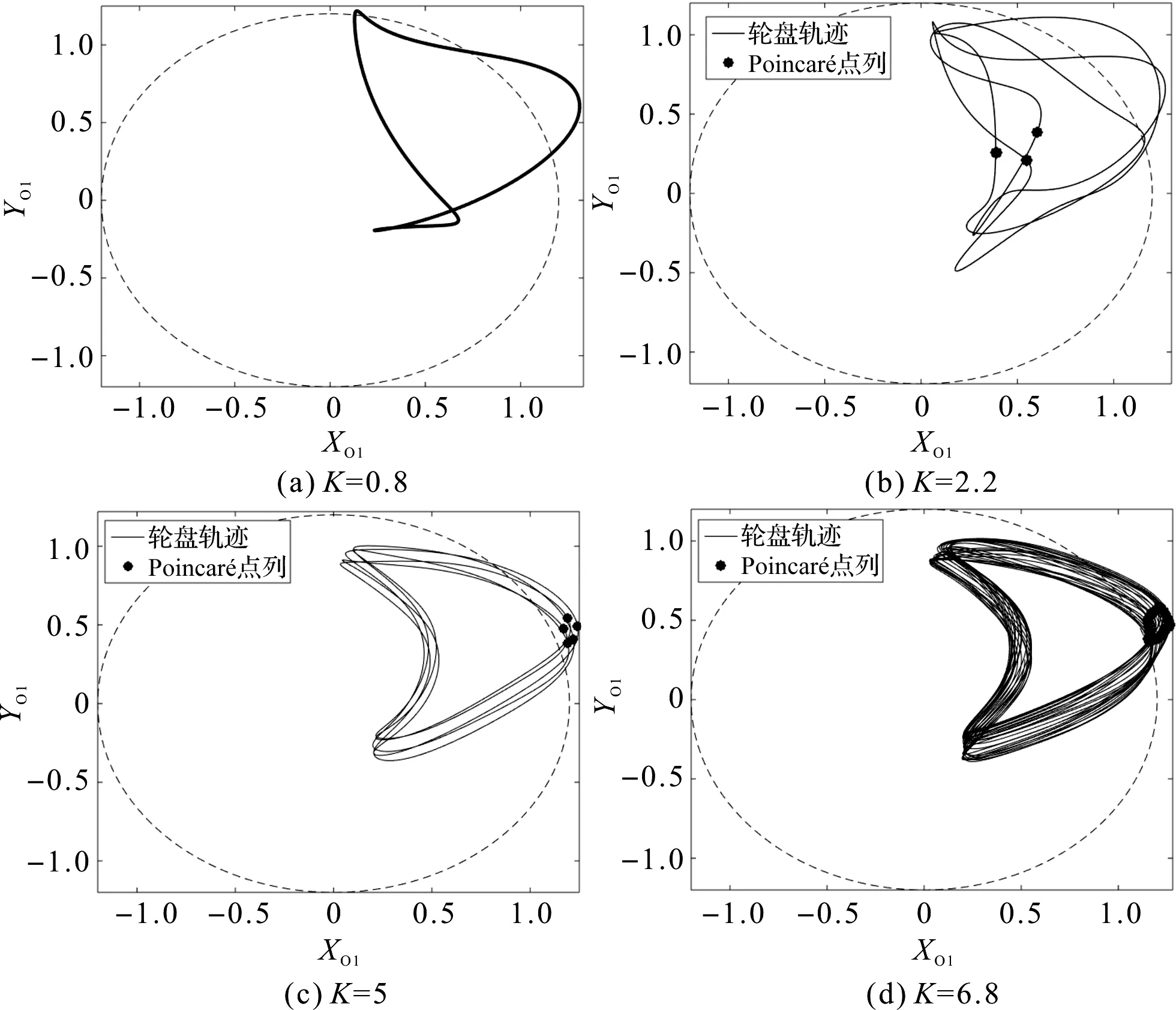
图9 不同拉杆刚度下轮盘O1的运动轨迹
当拉杆刚度较低时,转子主要呈现出周期运动,当K=0.8时的转子轮盘O1处的周期运动轨迹如图9(a)所示;
在周期运动区间中,当K=2.2时,转子运动呈现出短暂的周期三运动,图9(b)给出了转子轮盘O1处的周期三运动轨迹及Poincaré映射;
随着拉杆刚度的不断增加,转子的运动行为表现为周期五运动和准周期运动。当拉杆刚度分别为K=5和K=6.8时,转子松动端的周期五和准周期运动轨迹及Poincaré映射如图9(c,d)所示。
3 结束语
针对在基座松动和碰摩故障的情况下拉杆转子非线性动力学问题,笔者建立了拉杆转子模型及其运动微分方程,对故障转子随无量纲转速、松动刚度和拉杆刚度变化时的非线性动力学响应进行了研究,结论如下:
(1)基于有限长轴承油膜力近似解析解,运用Newmark法求解了系统动力学响应。首先将4种情况下(无故障、仅有碰摩故障、仅有基座松动故障和兼有两种故障)的转子的运动进行了比较,结果发现存在碰摩和基座松动故障的转子分岔点后移,且其转速范围更广;同时,基座松动故障对转子的影响更大;
(2)分别以转速、松动刚度和拉杆刚度为控制参数,分析了其对转子系统动力学的影响;从结果可以看出,随着控制参数的变化,转子的运动行为非常复杂丰富,具体的运动表现有周期、倍周期、周期三、周期四、周期五、周期七、准周期和混动运动。
该研究可以为拉杆转子故障检测和判别提供一定的理论基础。
