材料性能对大展弦比机翼非线性静气动弹性特性的影响研究*
2020-12-24王军利李托雷李庆庆陆正午冯博琳
雷 帅,王军利*,李托雷,李庆庆,陆正午,冯博琳
(1.陕西理工大学 机械工程学院,陕西 汉中 723000;2.西北机电工程研究所,陕西 咸阳 712099)
0 引 言
为了提高气动性能,现代飞行器普遍采用高强度轻质复合材料以减轻重量,且结构普遍采用大展弦比机翼布局形式[1,2]。复合材料在飞机上的使用占比逐年增加,如复合材料在A350XWB客机的使用比例超过波音B787的用量高达52%[3]。
国内外很多学者研究了复合材料在机翼上的应用。田坤黉等[4]利用Hamilton变分原理推导得到机翼的运动方程,再使用MATLAB进行仿真,结果表明与复合材料机翼相比,全铝合金机翼的固有频率明显减小;史旭东等[5]基于遗传算法,对大展弦比复合材料机翼的结构进行了优化设计,采用复合材料代替金属材料达到了减重效果;刘国春等人[6]对全复合材料大展弦比机翼进行了设计,在相同气动载荷作用下,复合材料机翼刚度提升了20%,结构减重了32%;王通等[7]通过等强度法分别建立了全金属机翼、半复合材料机翼和全复合材料机翼,对比发现半复材机翼比全金属机翼减重35%左右,全复材机翼比全金属机翼减重50%;DLUGOSZ[8]以提高强度和刚度以及减少结构的重量为优化的目的,对复合材料无人机结构进行优化设计。YI等[9]将半分析灵敏度分析技术植入ANSYS来实现复合机翼的可选设计,使得机翼结构的总质量减少了约24%;LIANG等[10]以机翼蒙皮板的层厚度为优化的设计变量,以结构重量最小为优化目标,以强度/应变为约束,对机翼的气动弹性进行了优化;周磊[11]以复合材料的铺层厚度为设计变量,以气动弹性和强度/应变为约束条件,对大展弦比复合材料机翼进行了结构优化设计,并分析了铺层比例和铺层非均衡对蒙皮铺层参数的影响。
综上所述,目前国内外对复合材料机翼的研究主要集中在机翼的结构优化及气动弹性优化上,而在复合材料对机翼纵向气动特性及稳定性影响研究的很少。
因此笔者考虑几何非线性对大展弦比机翼纵向气动特性及稳定性的影响,对不同攻角下,等厚度的复合材料机翼和铝合金机翼模型进行数值计算,并对两种机翼的结构特性、纵向气动特性及稳定性进行比较。
1 计算方法
基于松耦合的双向流固耦合计算流程如图1所示。
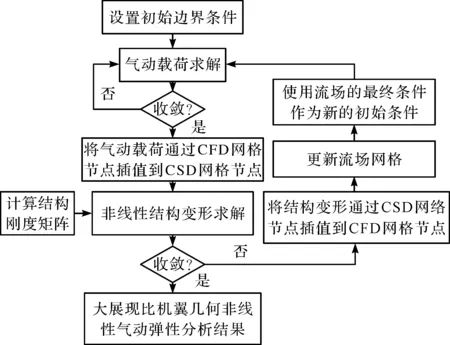
图1 松耦合计算流程
1.1 气动力求解技术
在静气动弹性问题中,忽略加速度以及变形速度对气动力的影响。笔者采用直角坐标系下积分形式的N-S方程为控制方程[12,13],即:
(1)

笔者选择S-A湍流模型[14]对流场进行数值模拟,粘性项采用中心格式[15]进行离散,对流项采用二阶精度的Roe-FDS迎风格式[16]来离散。
对于定常流动问题,控制方程的离散形式为:
(2)
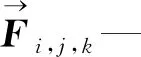
1.2 非线性结构方程求解技术
非线性结构的平衡方程如下:
[K]{u}={F}
(3)
式中:[K]—结构刚度矩阵;{u}—自由度位移矢量;{F}—外部气动力载荷矢量。
对线性变形问题,外载荷{F}和刚度矩阵[K]在计算前就已经确定,外载荷{F}和结构变形{u}为线性关系,只需一次求解,就能得出结构变形{u}。对于结构大变形几何非线性问题,刚度矩阵[K]由3部分构成,即:
[K]=[Kinc]+[Ku]-[Ka]
(4)
式中:Kinc—主切向刚度矩阵;Ku—大位移刚度矩阵;Ka—初始载荷矩阵。
求解主切向刚度矩阵即线性有限元刚度矩阵,只与结构初始构型相关;大位移刚度矩阵,包含结构几何形状变化效应;初始载荷矩阵,包括刚度关系中载荷方向变化效应。可见求解大变形几何非线性结构平衡方程时,需要不断更新结构刚度矩阵[K],且[Ku]和[Ka]均是结构变形{u}的函数,所以结构刚度矩阵[K]也是{u}的函数。因此,给定外载荷{F}后不能直接求解出结构变形{u},而只能采用逐步加载的迭代方法求解。本文采用牛顿-拉普森法[18]迭代方法求解非线性结构平衡方程。
2 方法验证
笔者以HIRENASD机翼模型为研究对象,对几何非线性静气动弹性计算方法的准确性进行验证。
机翼模型的几何尺寸[19]如图2所示。
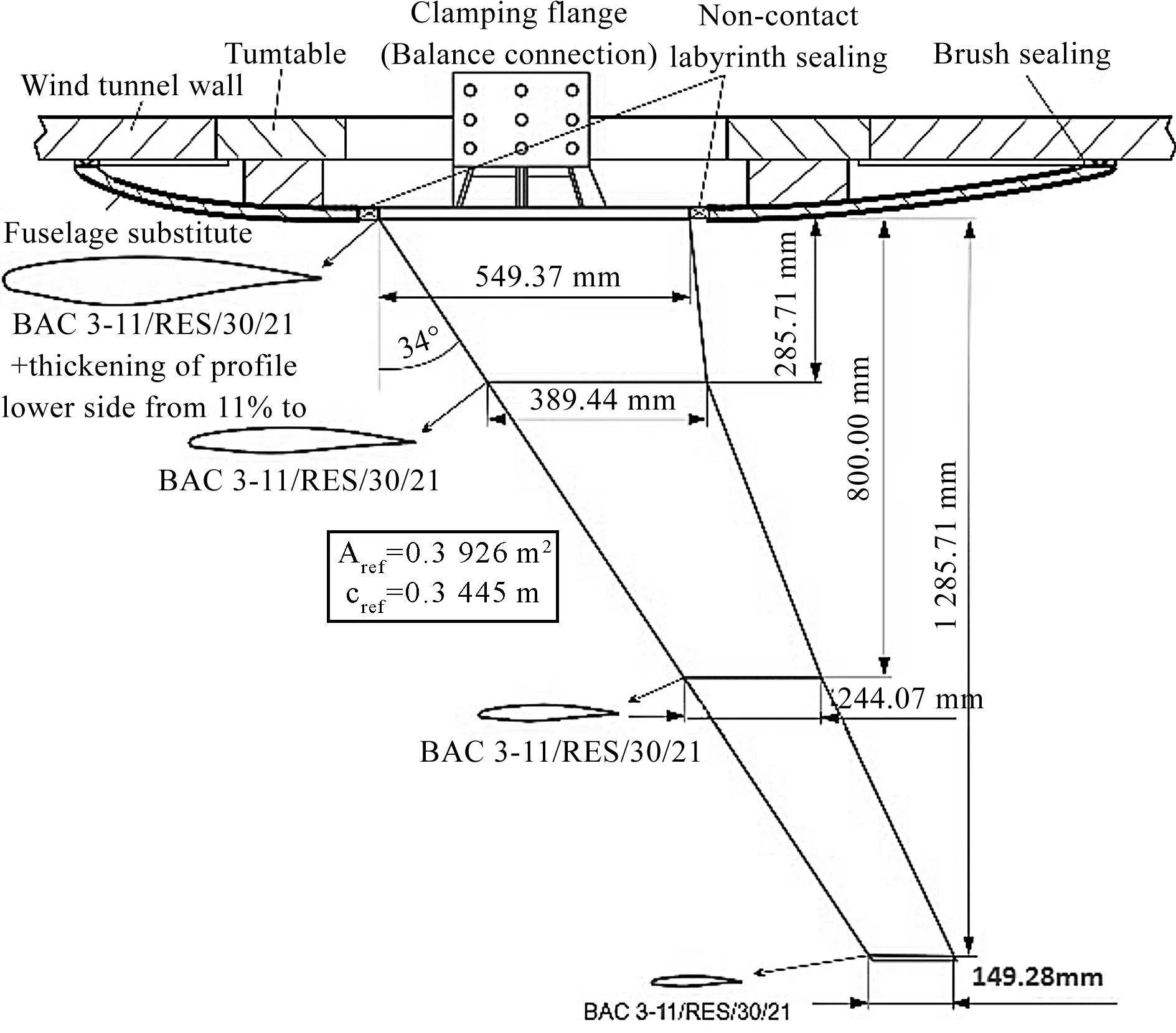
图2 HIRENASD机翼模型几何尺寸
HIRENASD机翼为超临界BAC3-11/RES/30/21翼型。参考面积为0.392 6 m2,参考长度为0.344 5 m。
用于数据对比的点A及2个展向位置2x/b=0.14和2x/b=0.95如图3所示。
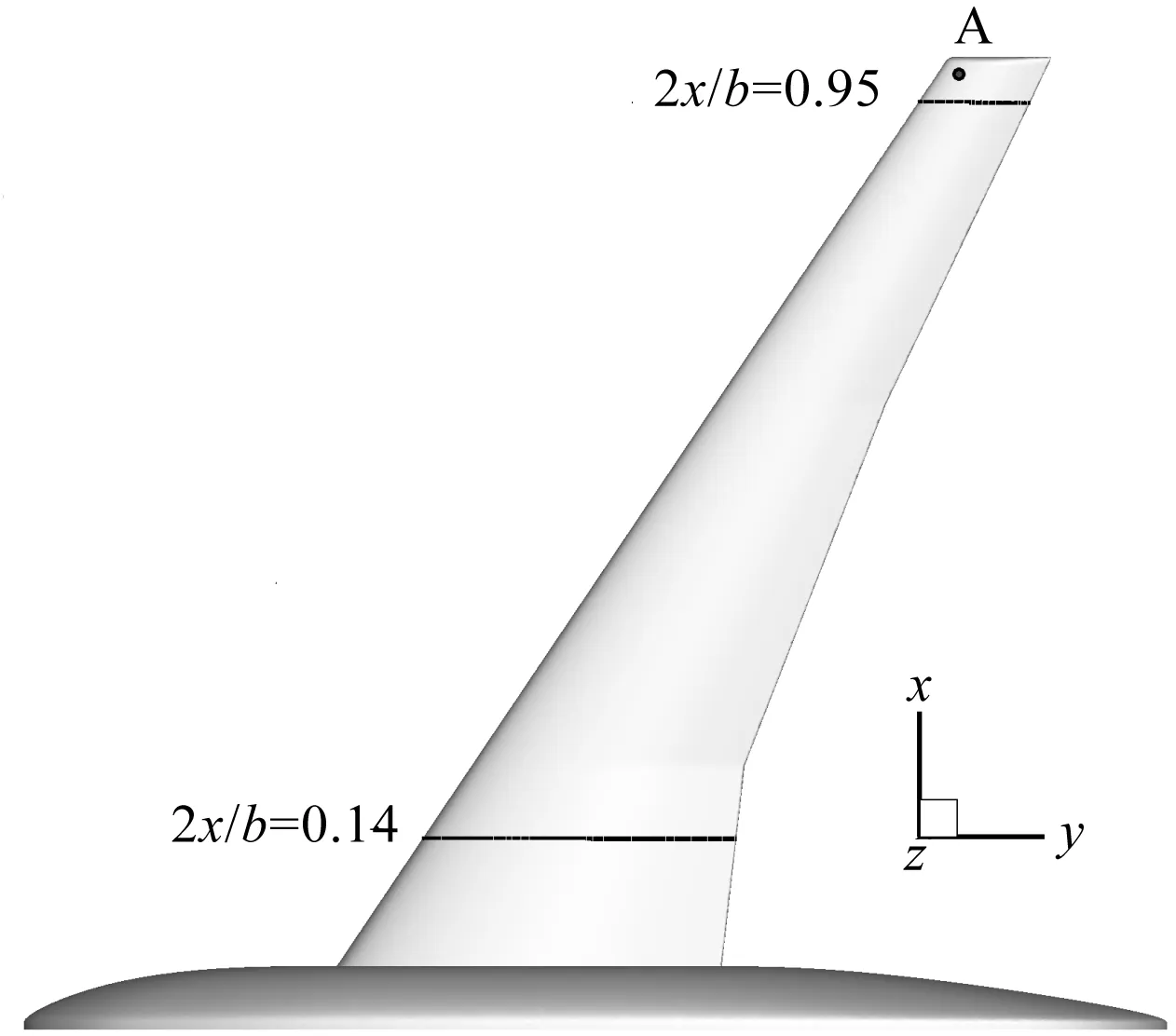
图3 HIRENASD机翼2个展向位置x—从对称面到展向的位置;b—展长
HIRENASD机翼流场及结构网格划分如图4所示。

图4 HIRENASD机翼流场及结构网格划分
当几何非线性气动弹性计算时,流场采用非结构网格,网格单元数为1.1×106。机身根部所在平面设置为对称边界条件,机翼与机身设置为物面边界条件,其余设置为压力远场边界条件。HIRENASD机翼几何非线性有限元结构模型采用非结构四面体网格划分,共有结构节点90 963个,结构网格单元51 747个,采用根部固定约束。
笔者计算的马赫数为0.8,雷诺数为7×106,攻角分别为-1.5°、0°、1.5°、3°和4.5°,并将计算结果与实验值[20]进行比较。
攻角为1.5°时,机翼2个展向位置的压力系数Cp与实验值的比较如图5所示。
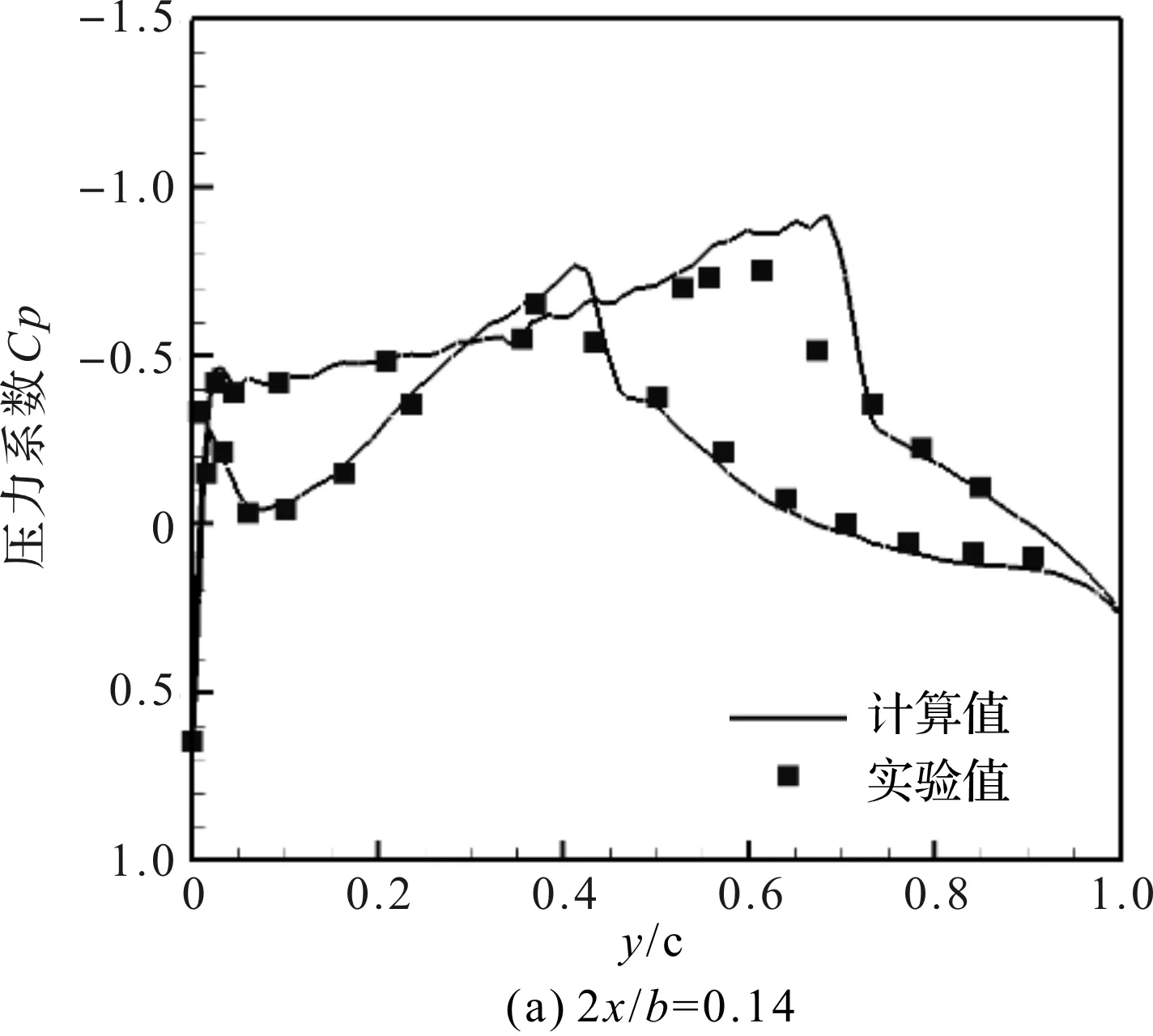
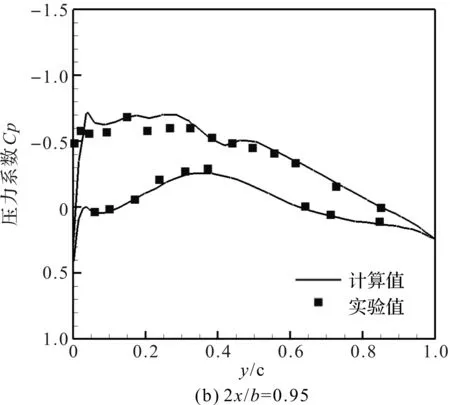
图5 攻角为1.5°时HIRENASD机翼不同展向位置压力系数分布与实验值比较
通过比较发现数值模拟的结果与实验结果吻合较好,证明了本文流体计算方法的可靠性。不同攻角下机翼实验对照点A点在Z方向的变形计算值与实验对比如图6所示。
由图6可知,本文计算数值与实验数值吻合良好,说明所提出的静气动弹性数值模拟方法可用于大变形几何非线性静气动弹性问题的分析。
图5和图6中计算值和实验值存在一些偏差,主要由于计算模型与实验模型、计算与实验条件的偏差引起的。
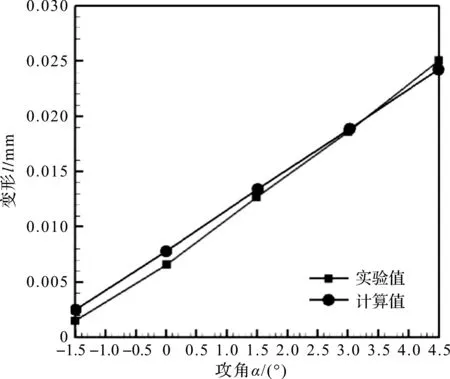
图6 不同攻角下HIRENASD机翼在Z方向的变形与实验值比较
3 数值模型和网格生成
大展弦比机翼模型的几何尺寸及3个展向位置如图7所示。
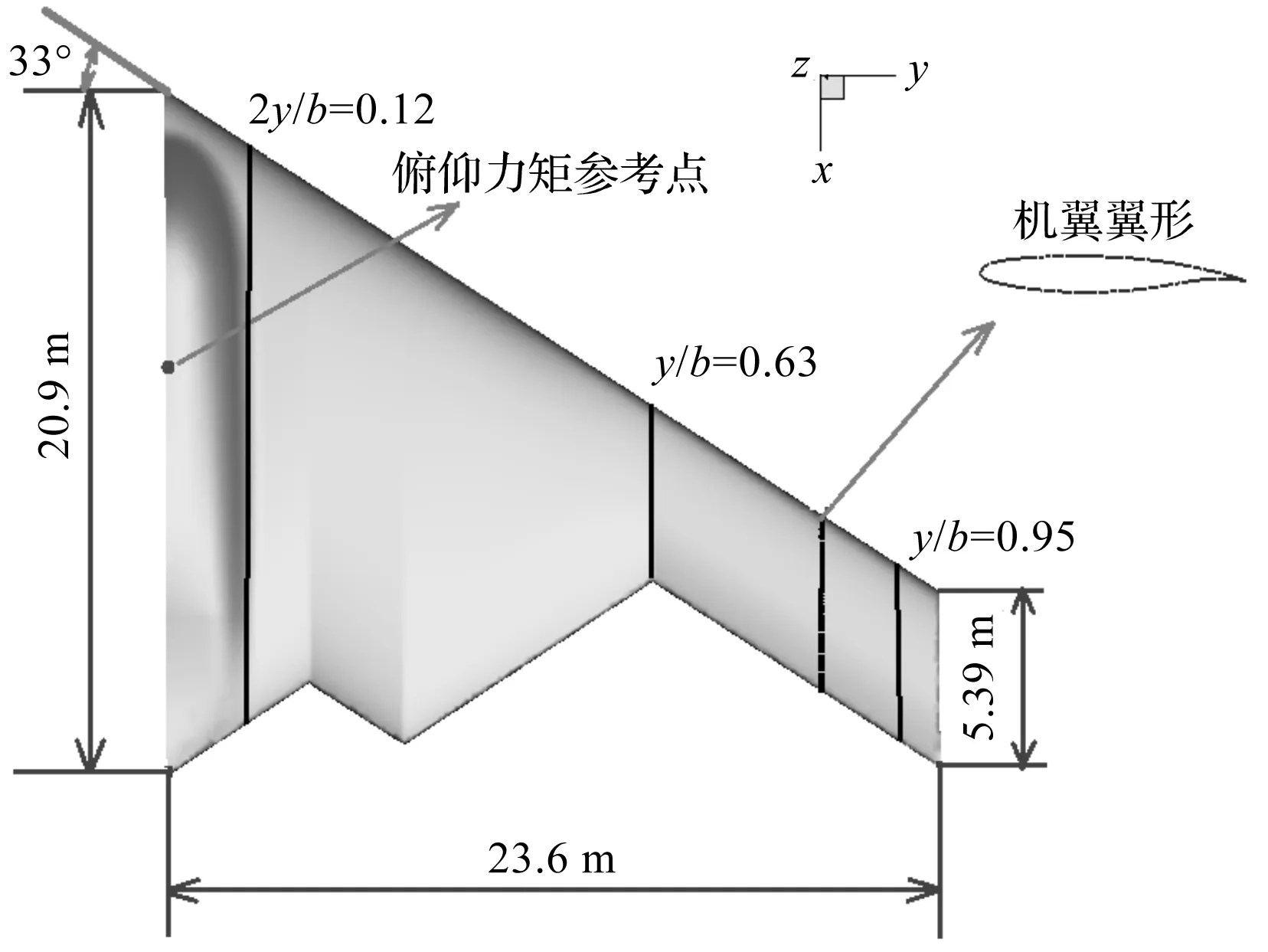
图7 大展弦比机翼模型几何尺寸及机翼展的3个展向位置
机翼的参考面积为240 m2,参考长度为12.94 m,俯仰力矩参考点距离机翼前缘8.23 m。复合材料机翼的梁和肋的厚度为20 mm,蒙皮的厚度为10 mm,梁和肋的材料为铝合金材料,机翼蒙皮为碳纤维复合材料。复合材料采用非对称铺层的方法,机翼蒙皮的铺层方式为[-45/453/90/-45/90/-45/45]中间层厚度为2 mm,其余每层厚度为1 mm。
复合材料参数如表1所示。

表1 碳纤维复合材料Epoxy Carbon UD (230 GPa) Prepreg参数
复合材料机翼的重量为18 928 kg,具有相同厚度的铝合金机翼的重量为25 562 kg,复合材料机翼减重达25.95%。
大展弦比机翼结构及流场计算域网格划分如图8所示。
机翼模型采用shell181壳体单元进行网格划分,生成节点数为171 429个,网格数为915 316个,在机翼翼根添加固定约束;机翼流场计算域采用非结构四面体网格进行网格划分,生成网格单元数为122 280个。机翼根部设置为对称边界条件,机翼设置为物面边界条件,其余边界设置为压力远场条件。
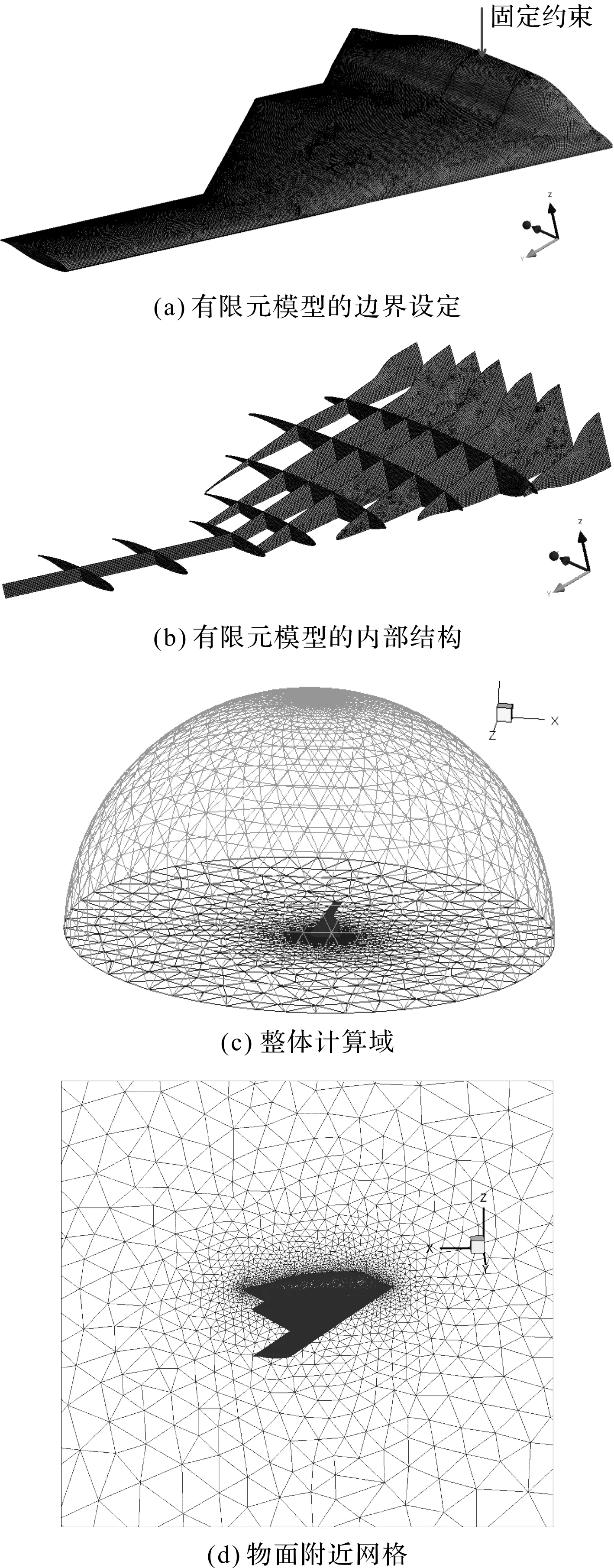
图8 机翼结构及流场计算域网格划分
4 计算及结果分析
4.1 材料性能对机翼几何非线性静气动弹性变形影响
笔者计算雷诺数4.06×107,远场压强11 737.6 Pa,马赫数为0.8时,攻角分别为0°、2°、4°、6°和8°时,两种机翼的非线性弹性变形情况。
马赫数为0.8,攻角为2°时,铝合金机翼和复合材料机翼的后缘沿升力方向的变形和沿翼展方向机翼扭转角的对比如图9所示。
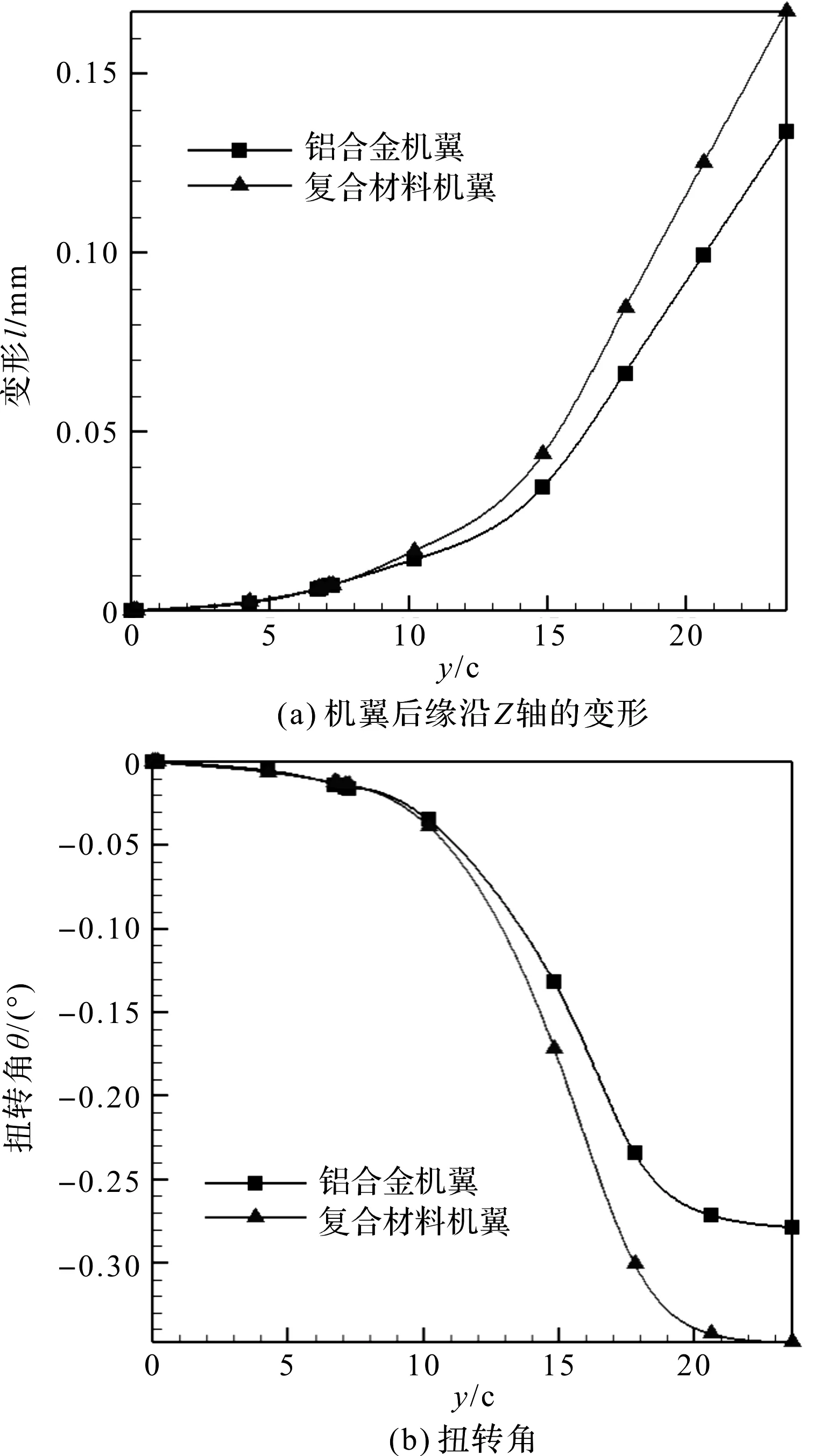
图9 铝合金机翼与复合材料机翼后缘在Z方向的变形及扭转角对比
从图9可以看出,机翼的变形及扭转角主要集中在机翼的外翼段,复合材料机翼在升力方向的变形和扭转角均大与铝合金机翼。
不同攻角下,铝合金机翼和复合材料机翼在Z轴方向的最大变形及最大等效应力对比曲线如图10所示。
由图10可知,两种机翼沿升力方向的变形和等效应力均随着攻角的增大而增大,并且复合材料机翼增大的幅度大于铝合金机翼增大的幅度。主要由于复合材料蒙皮铺层方法使得复合材料机翼刚度低于铝合金材料机翼刚度引起的。
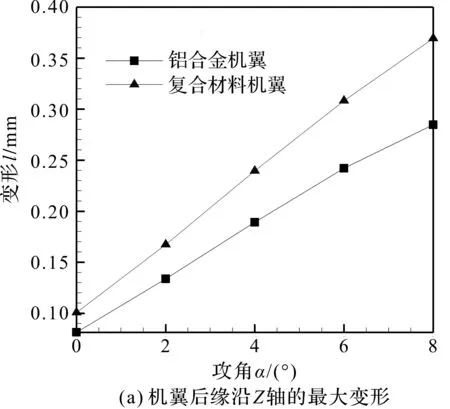
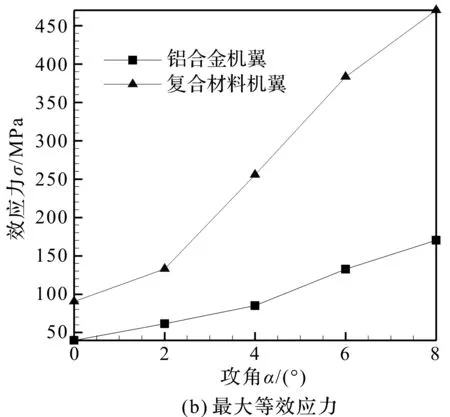
图10 不同攻角下两种机翼在Z方向的最大变形及最大等效应力对比
4.2 材料性能对机翼纵向气动特性及稳定性影响
笔者研究不同攻角下,几何非线性弹性变形对复合材料机翼和铝合金机翼纵向气动特性及稳定性的影响。
马赫数为0.8,攻角为2°时,复合材料机翼和铝合金机翼在几何非线性变形后不同展向位置压力系数比较如图11所示。
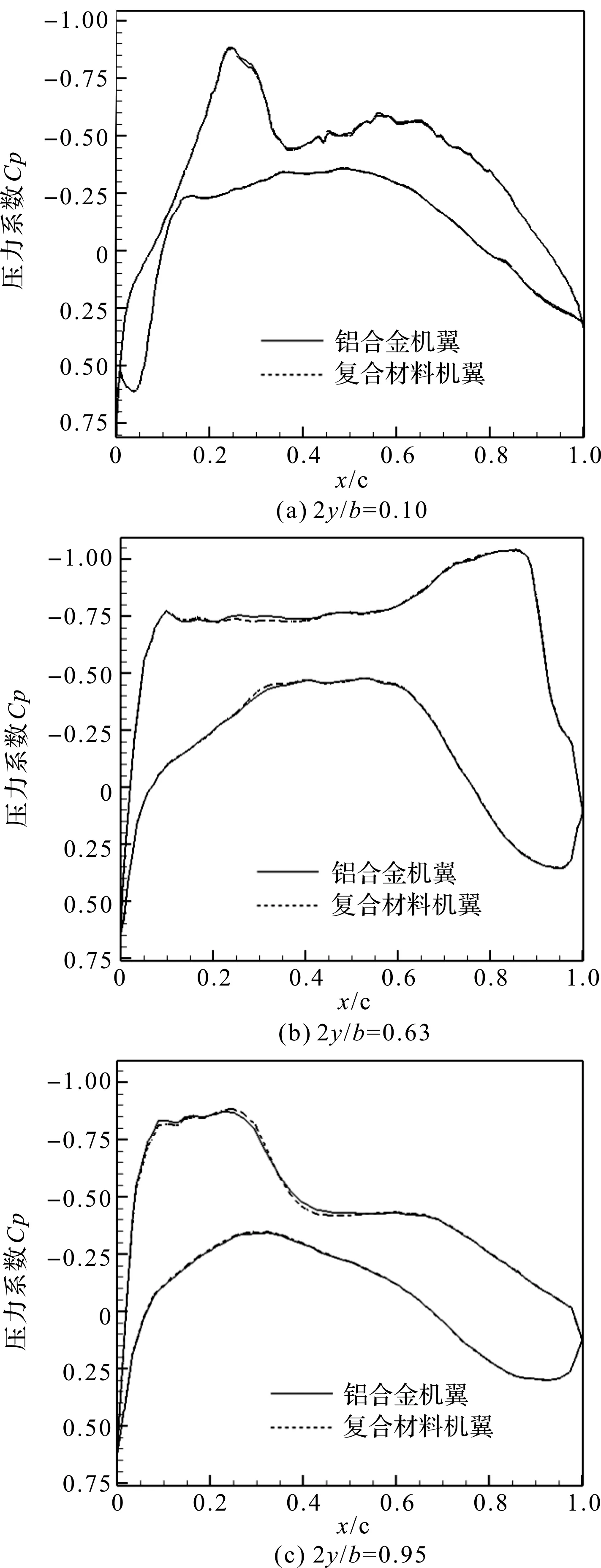
图11 两种大展弦比机翼压力系数分布比较
由图11可以看出,当展向截面位置2y/b<0.63时,复合材料机翼与铝合金机翼相比压力系数基本重合;当展向截面位置2y/b>0.63时,复合材料机翼与铝合金机翼相比,机翼前缘的压力系数发生较小变化。这主要是因为在翼根部分,两种机翼产生的变形都很小,几何非线性静气动弹性变形对机翼压力系数影响不大,越靠近机翼顶端,复合材料机翼产生的非线性变形和扭转角比铝合金机翼大,几何非线性静气动弹性使得复合材料机翼与铝合金机翼相比前缘的压力系数发生较小变化。
复合材料机翼和铝合金机翼升力系数、阻力系数、升阻比及静稳定曲线的比较如图12所示。
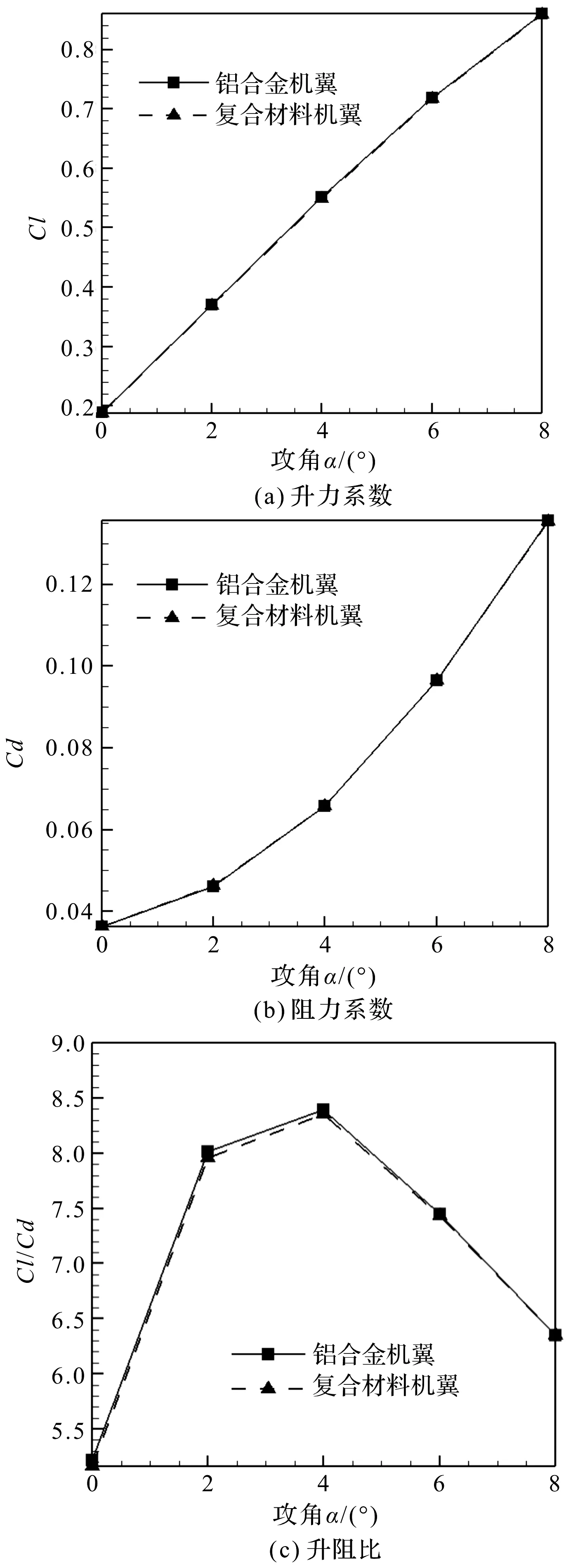
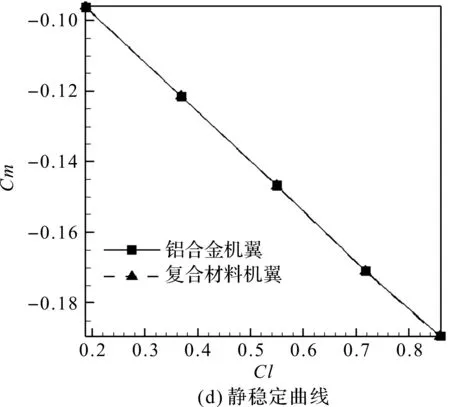
图12 静气动弹性对机翼纵向气动特性的影响
由图12可以看出,复合材料机翼与铝合金机翼相比,升力系数、阻力系数和静稳定裕度没有明显变化;复合材料机翼与铝合金机翼相比升阻比稍有减小。主要因为两种机翼的变形和扭转角主要发生在机翼的外翼,并且外翼段的面积较小,因此对气动力系数影响不大。
5 结束语
本文基于CFD/CSD双向流固耦合方法,对不同材料大展弦比机翼静气动弹性进行了数值模拟,得到了不同攻角下两种材料机翼的非线性弹性变形情况,分析了非线性静气动弹性对两种机翼结构特性、纵向气动特性及稳定性的影响,结果表明:
(1)厚度相同条件下,复合材料机翼在Z轴方向的变形、扭转角及等效应力均比铝合金机翼大。由于复合材料的各向特异性,复合材料铺层层数、铺层角度和铺层厚度对结构的性能有较大影响,本文铺层方法,使得复合材料机翼的结构刚度有所降低,但复合材料机翼重量与铝合金机翼相比减轻了25.95%;
(2)厚度相同条件下,复合材料机翼静气动弹性计算表明,在机翼外翼段,复合材料机翼变形及扭转角显著增大。由于外翼段面积较小,对机翼的升力、阻力影响较小。因此,复合材料机翼与铝合金机翼相比,升力系数、阻力系数及静稳定裕度均没有明显变化。
