基于ISTA的混合激励EMT金属探伤系统研究*
2020-12-24孙春光曾星星冯肖维
孙春光,何 敏,曾星星,冯肖维
(上海海事大学 物流工程学院,上海 201306)
0 引 言
经济的发展离不开高质量的金属材料,但在生产、加工、使用过程中,金属材料表面很可能会出现多种缺陷,尤以裂纹占比最大。在工业生产中,这些缺陷严重时将造成重大人员伤亡及财产损失,极大影响企业的生产和经营。
无损检测技术,如射线检测、磁粉检测、超声波检测等技术相继在金属探伤中得到应用[1-5]。信息技术的高速发展需要智能化的检测方法,其中探伤的图像化、可视化是无损检测技术的一个重要研究方向[6]。电磁层析成像(EMT)技术属于过程层析成像(process tomography, PT)的一种[7],将其用于金属材料探伤过程,不仅符合其电磁检测的基本特性,更由于其拥有的图像重建理论和方法,可满足探伤可视化的需求。
EMT用于金属探伤和成像的研究中,传感器的设计、图像重建质量的提高等问题也是研究重点[8]。采用混合激励的EMT金属探伤传感器,可增加独立的测量信息。
笔者在分析线性反投影(LBP)算法、Landweber迭代算法[9]、截断奇异值分解(TSVD)算法[10]、Tikhonov正则化算法[11]、迭代软阈值算法(ISTA)后,经过软件仿真和硬件实验对比,最后使用ISTA构建EMT金属探伤系统。
1 EMT金属探伤系统的构建与混合激励的分析
1.1 EMT金属探伤和成像系统结构
EMT金属探伤和成像系统的工作原理可描述为:将EMT传感阵列放置于金属体表面,在传感阵列的部分线圈上施加激励信号,并产生激励磁场[12],被测金属体表面的缺陷情况将影响激励磁场,采集传感阵列中检测线圈上的感应电压,可以获得被测金属表面电导率分布,即裂纹的位置信息,根据图像重建算法实现被测金属体表面缺陷的可视化。
此处使用的EMT探伤和成像系统由控制器、激励源、信号调理电路、传感器、多路选通模块、上位机6部分组成。系统结构框图如图1所示。

图1 系统结构框图
图1中,控制器使激励源输出一定频率的正弦信号,经过信号调理电路的放大、滤波后施加在传感器的激励线圈上,检测线圈的感应电压经过信号调理电路的整流、滤波,变成直流信号,经过控制器的模数转换后,送入上位机进行图像重建。
1.2 混合激励的6线圈传感器
过程层析成像技术的基本原理是Radon变换和Radon逆变换。设f(x,y)为定义在二维空间R2上的连续有界函数,一般将函数f(x,y)称为图像。图像重建属于逆问题求解,而该逆问题具有病态性,从检测数据方面降低病态性的方法是增加传感器线圈数量,但该方法增加了成本和系统的复杂性。
笔者使用混合激励方式采集数据,在不增加传感器线圈数量的情况下,仅通过修改程序即可调整激励方式,进而获得更多测量数据,降低了EMT系统的病态性,使f(x,y)更加逼近真实的物场信息,最终提高了图像质量。
此处使用的传感器采用6线圈结构,传感器实物如图2所示。

图2 传感器实物
为了使所有线圈在同一水平面上,传感器线圈按照圆形排列,被固定在2 mm厚的透明、非导磁、非导电塑料底板上;传感器有效测量范围为方形框线内。
测量过程描述如下:首先将6线圈传感器放在无缺陷金属板上,获得“空场”测量数据,然后将具有设定好缺陷的金属板(材料特性与无缺陷金属板相同)放在传感器下方,再次采集测量数据,经过归一化计算后得到灵敏度矩阵S;将传感器放在被测金属表面,获得检测数据B,在上位机中使用图像重建算法获得电导率分布矩阵G,即缺陷分布情况。
实际检测时,在常规6线圈检测方法中,若使用单线圈激励,例如将1号线圈作为激励线圈,2-6号线圈作为检测线圈,共有30种电压数据;若使用相邻线圈激励模式,例如将1号和2号作为激励线圈,分别检测余下线圈,共24种电压数据。单独使用时,获得的独立测量信息较少。
此处使用的6线圈传感器,不但将单线圈激励与相邻线圈激励相结合,而且增加了相对激励和间隔一个线圈的双线圈激励。在使用相对激励时,例如将1号和4号线圈作为激励线圈,余下线圈作为检测线圈,共有12种检测数据;当采用间隔一个线圈的双线圈激励时,例如将1号和5号线圈作为激励线圈,共有24种数据。
该方法的优点是:(1)在不修改硬件结构时,激励组合方式由程序决定,增加了系统控制的灵活性;与单独一种激励模式相比,增加了独立测量的数据,采集到的物场信息更丰富;(2)同时增加了系统的容错能力,当某个线圈发生断路故障时,其他检测线圈采集到的数据仍能重建图像,增强了系统的鲁棒性。
因该系统用于静态检测金属表面裂纹,对实时性要求不高,可以增加线圈数量和激励方式。但根据系统实际使用情况,从检测数据到图像重建不能消耗太长时间,故线圈数量和激励组合方式不能过多。经实验测试,该方案约5 s刷新一次图像,可以满足现场使用需求。
2 金属缺陷的图像重建
2.1 EMT数学模型
EMT正问题是已知被测材料电导率分布,求检测线圈上的感应电压和灵敏度矩阵,正问题可以用下式表示:
(1)
式中:Vij—线圈i和线圈j之间的检测电压;D—检测区域的面积;σ—被测材料的电导率;F—灵敏度分布函数。
研究中通常使用有限元法求解EMT问题,假设满足如下条件:(1)敏感场为似稳场;(2)敏感场呈二维分布状态;(3)被测材料是线性的和各向同性的。
此时EMT问题中的敏感场满足的Maxwell方程组如下所示:
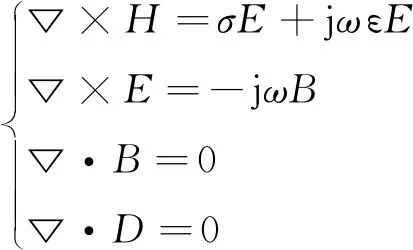
(2)
式中:B—磁感应强度;E—电场强度;H—磁感应强度;D—电位移矢量;σ—被测材料电导率;ω—激励信号的频率;ε—介电常数。
将上式变形可以得到下式:

(3)
式中:μ—被测材料的磁导率;J—激励信号的电流密度。
矢量磁位和磁感应强度有如下关系:
▽×A=B
(4)
式中:A—矢量磁位;B—磁感应强度。
将式(4)代入式(2),并结合式(3)经推导可得到下式:

(5)
式中:JS—线圈的电流密度。
根据有限元法可以得到磁感应强度B和矢量磁位A,最后得到检测线圈上的电压为:
(6)
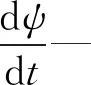
金属缺陷检测属于EMT逆问题求解。通常检测系统的非线性模型为:
v=F(σ)
(7)
式中:σ—电导率的分布情况;v—检测线圈上的电压矩阵;F—EMT系统固有的非线性不适定函数关系[13]。
式(7)可以用下式表示:
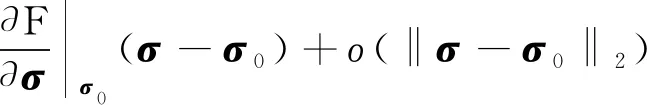
(8)
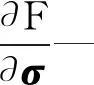
式(8)可以简化为:
v-F(σ0)=S(σ-σ0)
(9)
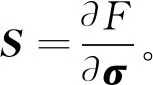
式(9)经化简可得:
B=SG
(10)
式中:B—被测金属电导率的变化引起检测线圈电压的变化量,B=v-F(σ0);G—和图像信息有关的电导率分布矩阵。
2.2 混合激励下的灵敏度矩阵
灵敏度矩阵的优良对图像重建效果有较大影响,常规EMT系统的灵敏度矩阵往往使用单一的激励得到[14]。笔者将多种激励时的灵敏度矩阵合并在一起,降低了系统的病态性。
设S1为单激励时的灵敏度矩阵,xi,j为灵敏度矩阵S1中的元素,则有下式:
(11)
(12)
式中:Vi,j—第i种激励时第j个像素点检测到的电压;Vi,em—空场条件下,第i种激励时的检测电压。
当传感器为两线圈激励时,设灵敏度矩阵为S2,其中yi,j为S2中的元素,则有下式:
(13)
(14)
式中:Vi,j—第i种激励时第j个像素点检测到的电压;Vi,em—空场条件下,第i种激励时的检测电压。
最终得到灵敏度矩阵S的表达式为:
(15)
根据式(11,15)可以明显看出,混合激励比单激励时的灵敏度矩阵信息更丰富,降低了系统的病态性。
2.3 常规图像重建算法
EMT的图像重建中,检测电压个数m远小于像素点个数n;因此,图像重建属于不适定逆问题,导致灵敏度矩阵S不是方阵,不能根据S的逆矩阵求式(10)中的电导率分布矩阵G。
通常解决不适定问题的方法是正则化,主要有两种方式:(1)利用关于被研究对象某些先验信息,从物理上引入定性或定量的约束以限制解集;(2)从数学方面提供解的补充信息或适当修改解的定义。
EMT技术中通常将该逆问题的求解转化为目标泛函的极值优化,即:
(16)
传统的线性反投影算法虽然简单、重建速度快,但成像质量相对较差,严格来说,仅是一种定性的算法;截断奇异值分解(TSVD)算法是截断较小的奇异值从而提高系统的稳定性,但会损失一部分有效信息;Tikhonov正则化是基于2范数的优化方法,适用于重建连续的、光滑的信号图像,而金属裂纹通常是突变的、不连续的;Landweber迭代法从数值最优化而言,本质上属于最速下降法,在迭代过程中不断修正电导率分布矩阵。
改进Landweber迭代算法是将Tikhonov正则化计算结果作为迭代初值,提高迭代计算的起点,其迭代格式为:
(17)
式中:I—单位矩阵;μ—正则化参数,一般是经验值;αk—松弛因子,和迭代步长有关。
其中:αk一般有2种方法确定:固定值法、最优步长法。
实际求解中,通常将αk设为固定常数α,此时的迭代格式如下所示:
Gk+1=Gk-αST(SGk-B)
(18)
可见上述方法仍然不能解决收敛速度较慢、半收敛的问题。因此,将这些算法用于电磁层析成像系统中,还都有待改善。
2.4 迭代软阈值算法
被测金属的缺陷一般只是整个检测区域的较小部分,因此所求的电导率分布矩阵是稀疏的,虽然迭代算法常用来重建稀疏信号,但仅用迭代无法得到准确结果;而借助凸优化理论将稀疏正则化问题转化为凸优化问题,需要计算大量矩阵数据。因此,寻找基于梯度运算、只有简单矩阵相乘的算法是必然选择,而迭代软阈值算法刚好符合这个要求。
笔者首次将ISTA引入到EMT金属探伤中,通过测量稀疏信号的噪声,再使用软阈值方法即可重构信号。该算法属于小波变换域,会对所有小波系数作等程度的衰减,并且求解过程简单,在声发射法检测压力管道泄露中已有应用[15],在CT图像重建中也有成功运用[16],此处用来解决EMT图像重建的逆问题。
已知灵敏度矩阵S和测量数据B,求电导率分布矩阵G,构造目标函数如下式所示:
(19)

根据Majorization-Minimization优化框架[17],优化后的目标函数如下所示:
(20)
式中:Z—第n次计算的电导率分布矩阵Gn,在每次迭代中通过收缩阈值更新G。

u(G,Z)≥f(G)u(Z,Z)=f(Z)
(21)
式(21)中的u(G,Z)可简化为:
(22)
其中:
与G无关,于是式(22)可等价为下式:
(23)
其中:G*=Z+ST(B-SZ),可得到ISTA优化问题的表达式为:
(24)
通过求解可得下式:
(25)
其中:G*=Gn+ST(B-SGn),根据Majorization-
Minimization优化框架的流程进行迭代,即可求得灵敏度分布矩阵G。
3 仿真与分析
为了对比混合激励和常规激励条件下不同图像重建算法的金属缺陷成像效果,笔者使用AnsoftMaxwell软件[18]进行仿真实验,根据前文传感器结构的介绍搭建了6线圈传感器模型。
仿真模型中的缺陷如图3所示。

图3 仿真模型中的缺陷
线圈匝数均为200,正弦激励信号的峰值为5 Vpp、频率为10 kHz,传感器线圈内侧为有效检测范围,分别采用混合激励和单线圈激励来检测圆形缺陷、横条缺陷、竖条缺陷的被测金属,最后用不同算法进行图像重建。
在仿真实验中,6线圈传感器分别使用单线圈激励和混合激励,使用扰动法获得不同激励下的灵敏度矩阵,然后分别使用Tikhonov正则化算法、改进Landweber迭代算法、ISTA,对不同形状缺陷的测量数据进行图像重建。
仿真数据的重建图像如图4所示。

图4 仿真数据的重建图像
图4中,颜色较深的部分代表缺陷的位置和形状,不同的颜色代表不同的电导率。可以看出:
(1)在缺陷相同时,相同激励下,改进Landweber迭代算法比Tikhonov正则化算法成像效果稍微有所改善;
(2)在缺陷相同时,使用相同算法,混合激励的图像重建效果明显比单激励图像完整;
(3)在缺陷相同时,混合激励下,ISTA效果在3种算法中最优。
4 实验验证
为进一步验证仿真实验的结论,笔者根据仿真模型设计了实验EMT探伤和成像系统。
系统实物如图5所示。

图5 系统实物
系统具体工作原理如下:
STM32控制器控制激励源,使其输出峰值为5 Vpp、频率为10 kHz的正弦信号,通过信号调理电路进行放大、滤波得到纯净的正弦激励信号,控制器控制多路选通开关,使激励信号施加到相应的激励线圈上,检测线圈因电磁感应产生相应的电压,感应电压经过信号调理电路的整流、滤波作用变成直流信号,送入控制器进行模数转换并获得数字信号,最后通过串口传送给上位机,使用图像重建算法获得被测金属的缺陷情况。
实验中的圆形缺陷半径为4 mm,长条缺陷宽度为2 mm,长度为10 mm,分别采用单独激励和混合激励,最后使用不同图像重建算法获得图像。
实验数据的重建图像如图6所示。
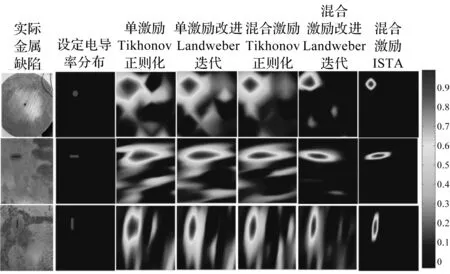
图6 实验数据的重建图像
图6结果显示:在缺陷相同时,使用相同算法,混合激励的重建图像明显优于单激励;而都采用混合激励时,迭代软阈值(ISTA)算法图像重建效果最好,由此验证了仿真实验的结论。
为了定量比较两种激励方式和不同图像重建算法的成像效果,笔者引用图像相对误差概念[19],其计算公式如下:
(26)
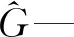
实验中重建图像的相对误差如图7所示。
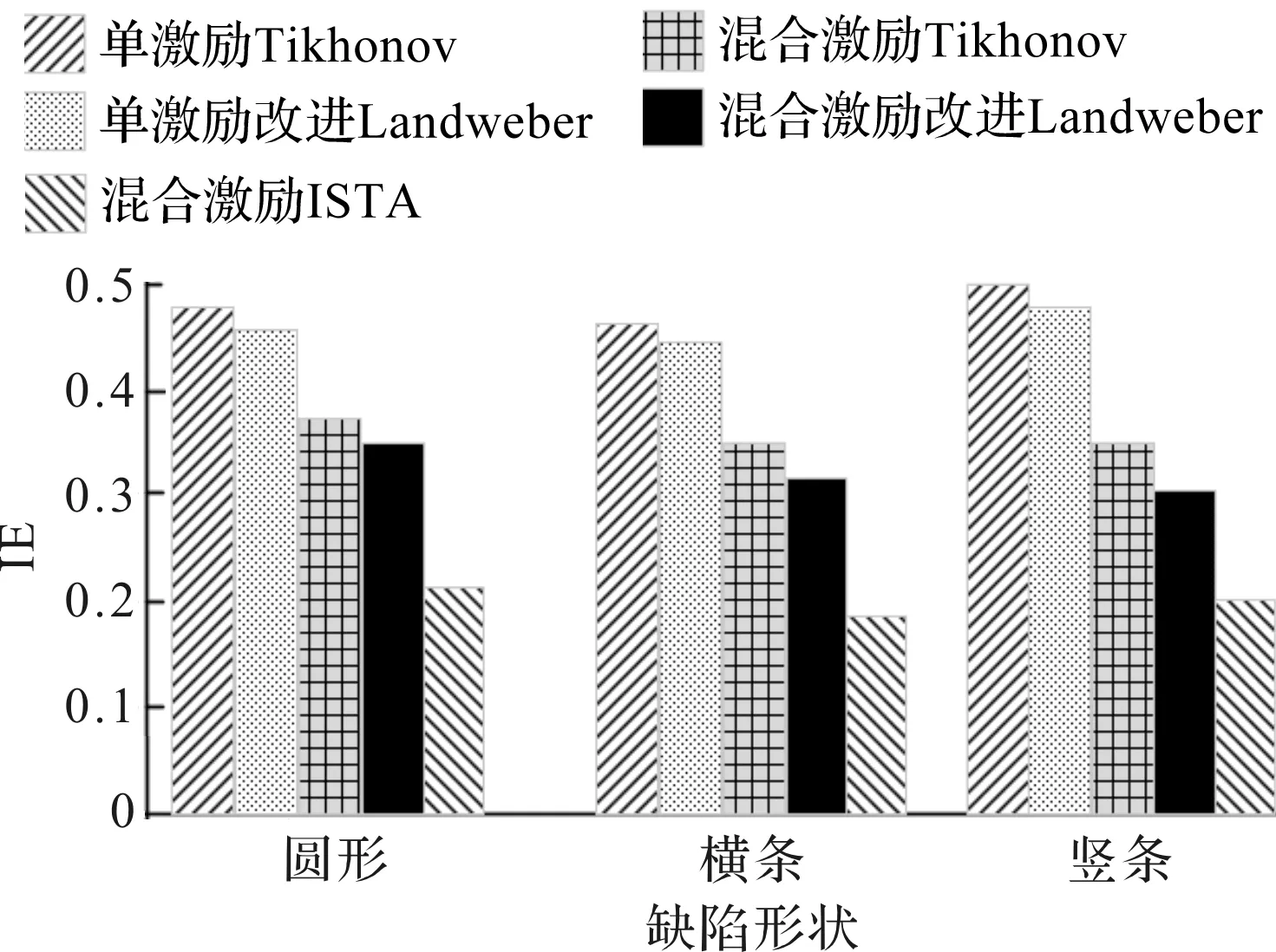
图7 实验中重建图像相对误差
由图7可以看出:在相同缺陷下,使用相同算法时,混合激励的图像重建误差小于单激励;而都采用混合激励时,ISTA的图像重建相对误差最小。
由此可以证明:在EMT系统中,混合激励和迭代软阈值算法能明显改善图像重建效果。
5 结束语
本文采用混合激励的EMT金属探伤和成像系统,建立了该激励下的灵敏度矩阵,降低了图像重建逆问题的病态性,增加了系统的容错能力,提高了鲁棒性;然后对比了Tikhonov正则化算法、改进Landweber迭代算法和迭代软阈值算法(ISTA);经对比仿真结果可知:在其他条件相同时,混合激励比单线圈激励的图像重建效果好;在其他条件相同时,ISTA比其余两种算法成像效果完整。
最后笔者搭建了硬件实验平台,使用实物测量的数据经不同图像重建算法进行了比较,验证了仿真实验的结论。
