基于AMESim-Simulink的自适应模糊PID电液比例位置控制研究*
2020-12-24李延民刘锡山庄天宇
李延民,刘锡山,王 振,庄天宇
(1.郑州大学 机械与动力工程学院,河南 郑州 450001;2.郑州大学 河南省资源与材料工业技术研究院,河南 郑州 450001)
0 引 言
近些年,随着桥梁建设的不断发展,用于重型大跨度桥梁的支座日益增多,对用于支座力学性能检测的压剪试验机设备要求也越来越高。压剪试验机主要用于各种桥梁板式、盆式、球式等隔震橡胶支座在抗压、抗剪切力复合条件下的轴向径向抗压、抗剪、允许转角等力学性能试验[1,2]。
液压控制系统是压剪试验机完成支座力学性能试验的核心组成部分,其控制性能的优劣直接关系到支座力学性能参数检测的精确度,影响对支座的质量评估,进而影响到桥梁安全,因此,其对于设备液压控制系统性能的研究优化有着至关重要的作用。
吴天宇[3]将直驱式泵控缸电液伺服液压控制系统应用于20 MN压剪试验机上,并通过调节PID控制参数,得到了系统的最佳响应;赵斌[4]在位置同步误差不理想的情况下运用根轨迹校正的方法,优化了电液比例位置同步控制系统性能,减小了系统控制误差。
总结相关文献,鉴于常规PID控制精度较低、抗干扰能力差、调节较慢等特点[5,6],笔者拟在水平剪切液压子回路中,采用多只同规格电液比例阀并联形成阀控缸系统,同时在系统中引入自适应模糊PID控制,利用AMESim-Simulink软件联合仿真实现PID参数的在线最优整定,对系统动态响应性、正弦实际工况加载精度、位移-力加载特性等方面进行研究。
1 加载系统
1.1 加载系统技术要求
最大竖向力:20 MN;最大水平剪切力:4 MN;最大水平位移:300 mm(以工件初始位置向两侧运动最大位移为300 mm)。在分析了实际工况的情况下,笔者根据JB/T 11582-2013标准,确定了剪切系统剪切频率为0.067 Hz,平均剪切速度为80 mm/s,加载次数为11次。
1.2 加载原理
在水平剪切过程中,支座在竖向作动器压紧恒定力作用下,水平剪切作动器带动剪切板对其实现往复剪切运动,用以检测支座的剪切模量、等效阻尼比等力学参数。
此处仅对水平剪切系统加以研究。该系统为实现动态加载,水平作动器采用双出杆双作用对称液压缸(规格:630 mm/400 mm)。优点是提供两侧对称的液压力,便于实现双向控制。为使剪切系统平稳运行,快速响应,达到较高的控制精度要求,笔者采用电液比例闭环位置控制,同时加入自适应模糊PID控制,从而使实际的加载路径能更好地跟踪期望的信号。
水平剪切加载原理如图1所示。

图1 水平剪切加载原理1—下压板;2—试件;3—导向块;4—上压板;5—框架;6—竖向作动器;7—竖向力、位移传感器;8—水平剪切板;9—水平力、位移传感器;10—水平作动器;11—升降作动器
图1以双剪工况为例,在此压剪试验机竖向压紧、水平剪切的过程中,采用竖向力和位移传感器检测竖向作动器输出力和竖向位移,水平力传感器和位移传感器检测水平作动器的剪切力和切向位移。
根据GB/T 20688.1-2007标准所述,系统在不变的竖向压力下对桥梁支座的水平剪切性能完成水平剪切测定。剪切过程中,竖向压力允许波动范围为±10%,水平位移允许波动范围为±5%[7]。
1.3 剪切子回路液压原理图
剪切系统液压子回路原理图如图2所示。
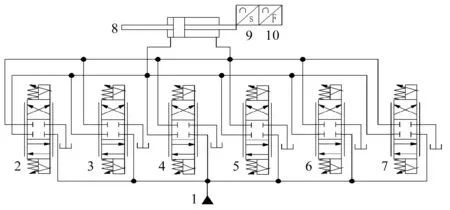
图2 剪切系统液压子回路原理图1—液压源;2,3,4,5,6,7—电液比例阀;8—水平剪切作动器;9—位移传感器;10—力传感器
图2中,剪切加载系统以工件初始位置为原点,左、右两方向运动工况相同,作动器采用双出杆双作用液压缸,实现对称加载,简化系统加载控制难度;
当加载系统工作达到1 262.6 L/min的瞬时超大峰值流量时,采用单只液压阀不能满足其流量需求,因此,笔者拟采用电液比例方向控制阀“并联”工作;
对比期望信号与实施位移,将信号差经处理器处理后传递给电液比例方向阀,控制方向阀的开口流量,实现对流量的准确控制,进而达到对作动器位置的精确控制。
1.4 载荷分析
桥梁支座通常置于桥面和桥墩中间,作为两者之间的柔性连接部件,除了承受来自桥面的重量之外,还要承受来自横桥向和顺桥向由于震动等因素造成的剪切力。因此,检测桥梁支座承受剪切的性能参数至关重要。
在支座的分析过程中,将支座水平剪切过程简化为一个弹簧-阻尼模型。水平作动器在剪切过程中不只提供支座剪切所需要的的水平力,还要克服惯性力、粘性阻尼力以及弹簧力等。
加载模型如图3所示。
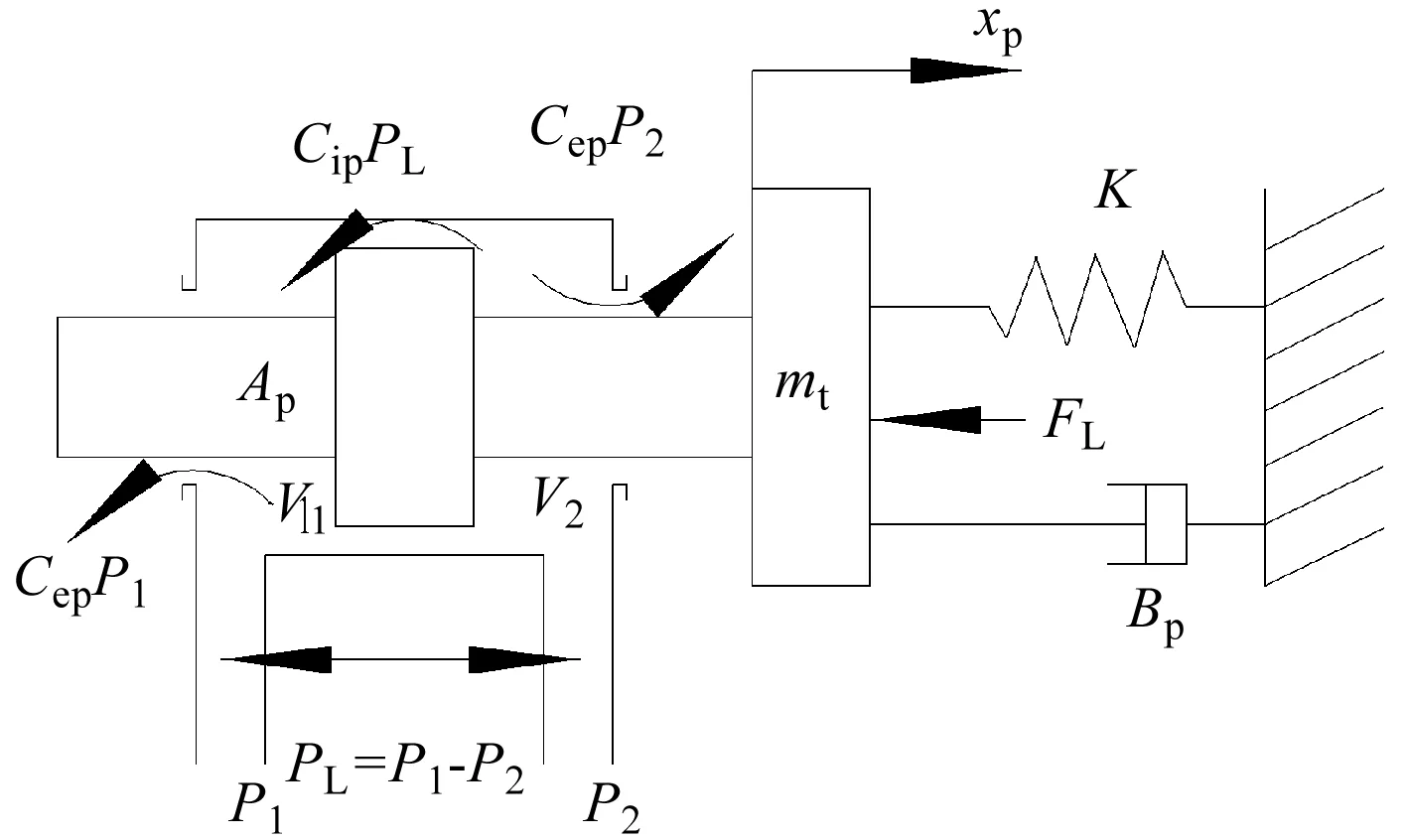
图3 加载模型
作动器的输出力和负载平衡方程为:
(1)
式中:mt—作动器-负载系统质量;Bp—作动器-负载系统粘性阻尼系数;K—系统负载弹簧刚度;FL—作用在活塞上的任意外负载力。
2 自适应模糊PID控制
2.1 常规PID与自适应模糊PID控制
常规PID控制是人为手动调整参数以获得良好的系统控制性能,但是其控制精度低,抗干扰能力差。为使系统具有更好的自适应性,笔者在常规PID控制基础上,结合模糊规则进行模糊推理,完成在线最优整定PID参数的要求,使系统具有更好的动态性能、更高的控制精度以及较好的鲁棒性[8-12]。
常规PID控制如图4所示。

图4 常规PID控制
自适应模糊PID控制如图5所示。

图5 自适应模糊PID控制
自适应模糊PID控制的核心在于模糊PID控制器的设计。其工作原理是将输入的偏差信号e(t)和偏差信号e(t)的微分de/dt传递给模糊PID控制器,控制器进行模糊推理,以及PID参数的在线整定[13]。
其原理如下式所示:
(2)
(3)
(4)
2.2 模糊控制器的设定
该模糊PID控制器[14,15]设置两输入-三输出,与方式(and method)为minimum,或方式(or method)为maximum,推理方式(implication)为minimum,合成方式(aggregation)为maximum,解模糊方式(defuzzification)为centroid;定义模糊规则输入变量e(t)和de/dt的模糊集合为{NB,NM,NS,ZO,PS,PM,PB},对应的域为{-6,-4,-2,0,2,4,6},定义模糊规则输出变量kp,ki,kd的模糊集合为{NB,NM,NS,ZO,PS,PM,PB},对应的域为[-6,6]。
模糊kp参数规则表如表1所示。
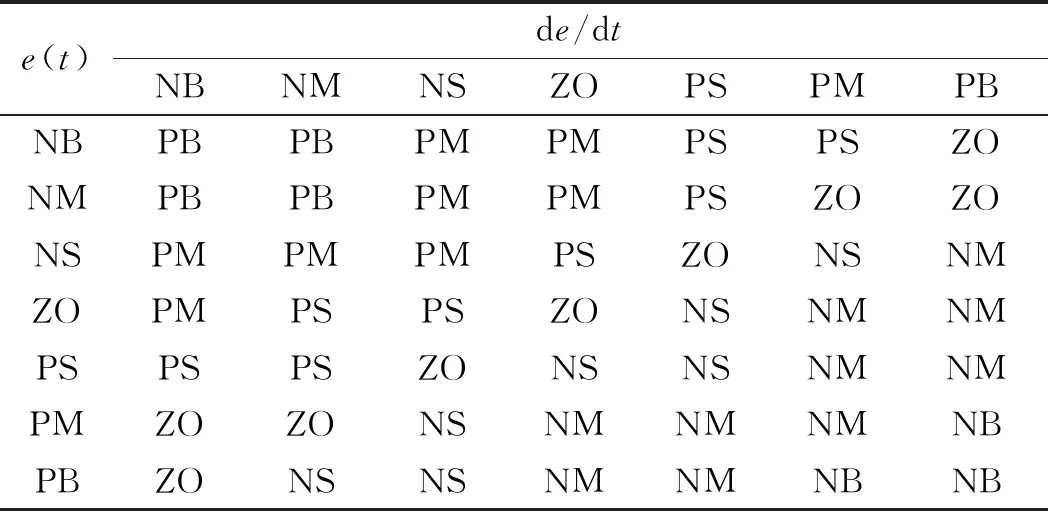
表1 模糊kp参数规则表
模糊ki参数规则表如表2所示。
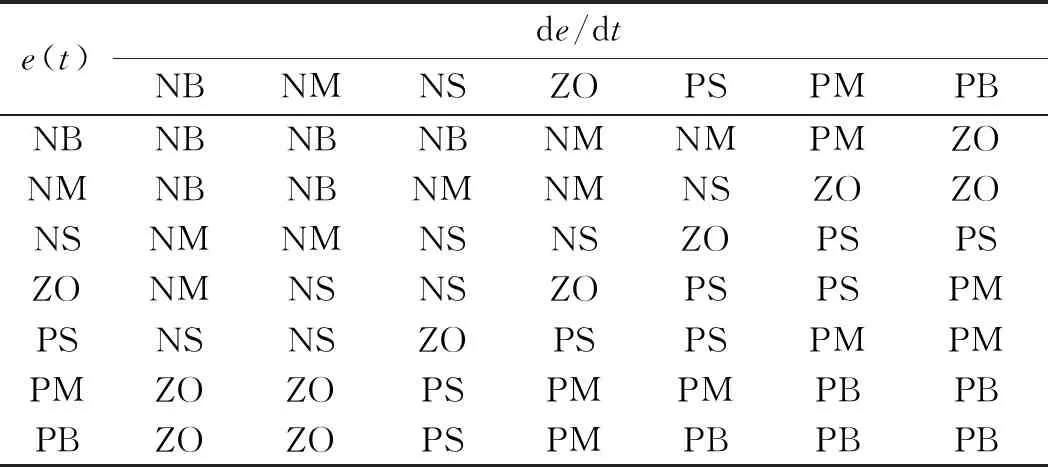
表2 模糊ki参数规则表
模糊kd参数规则表如表3所示。
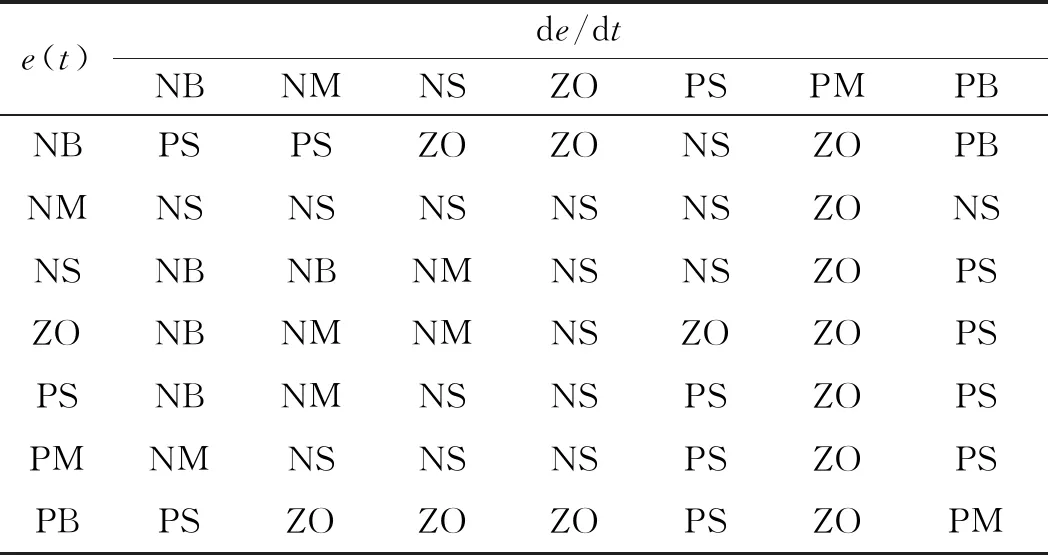
表3 模糊kd参数规则表
3 液压回路AMESim-Simulink联合仿真
MATLAB/Simulink是一款计算功能极其强大的仿真软件。但其在对液压系统建模时,需要做很多的简化工作,忽略很多的影响因素,使仿真结果与实际差别较大;而AMESim是专门应用于液压/机械系统的建模仿真软件,利用面向对象的图形化,可视化建模方式,使设计者更能专注于系统的设计,同时AMESim提供了同其他软件联合的丰富接口[16]。运用Simulink和AMESim进行联合建模仿真,可以得到更准确的仿真结果。
根据加载系统工况设计要求,笔者建立AMESim-Simulink水平剪切位移反馈仿真模型,同时建立Simulink控制模块。
AMESim-Simulink水平剪切位移反馈仿真模型如图6所示。
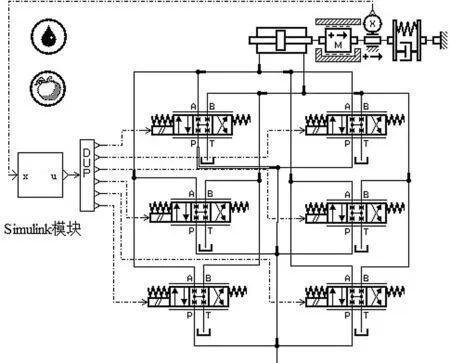
图6 AMESim-Simulink水平剪切位移反馈仿真模型
Simulink控制模块如图7所示。
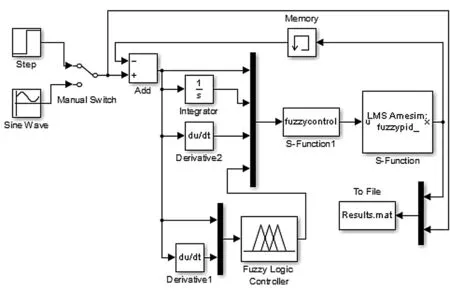
图7 Simulink控制模块
系统主要参数如表4所示。
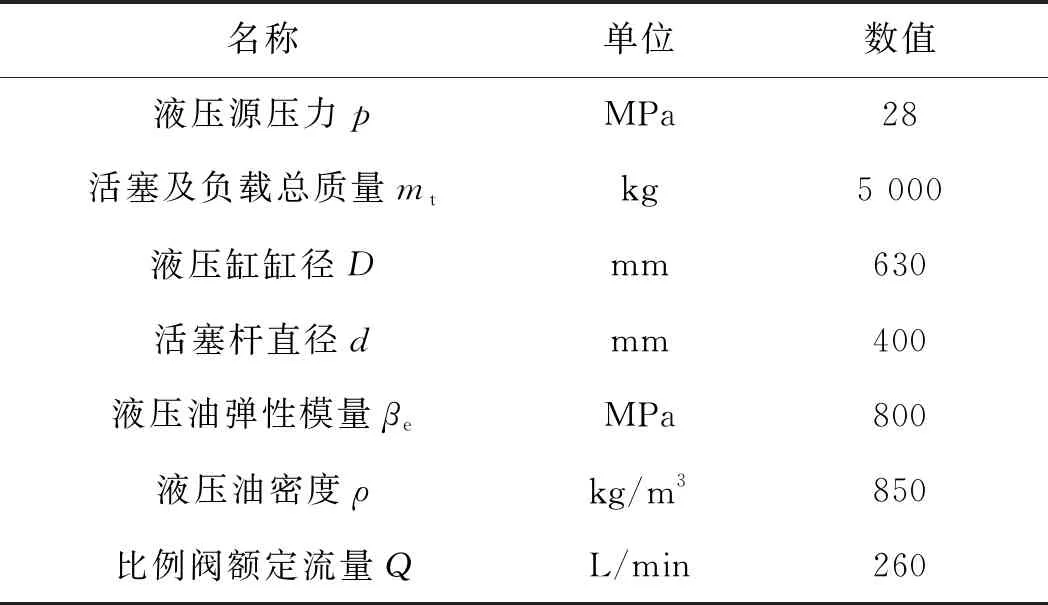
表4 系统主要参数
在系统中,输入幅值为0.1,在1 s处阶跃的阶跃信号,使用试凑法确定kp=6,ki=0.1,kd=0.01,先后在系统普通PID控制和自适应模糊PID控制下进行仿真,仿真时间4 s,步长0.01 s。
阶跃响应如图8所示。

图8 阶跃响应
从图8可以看出:引入自适应模糊PID控制后,系统超调量、震荡次数显著降低;常规PID控制曲线历时1.82 s达到稳态,自适应模糊PID控制曲线历时1.36 s达到稳态,达到稳态时间明显缩短,并且系统超调量由4.4%降至2.38%。由此可见,该系统的控制特性得到了很好的优化。
根据GB/T 20688.1-2007橡胶支座第一部分:隔震橡胶支座试验方法规定,理想加载路径为正弦函数曲线,平衡位置为0.4 m,幅值为0.3 m,加载频率为0.067 Hz,设置仿真时长160 s,步长为0.01 s。
加载位移图如图9所示。
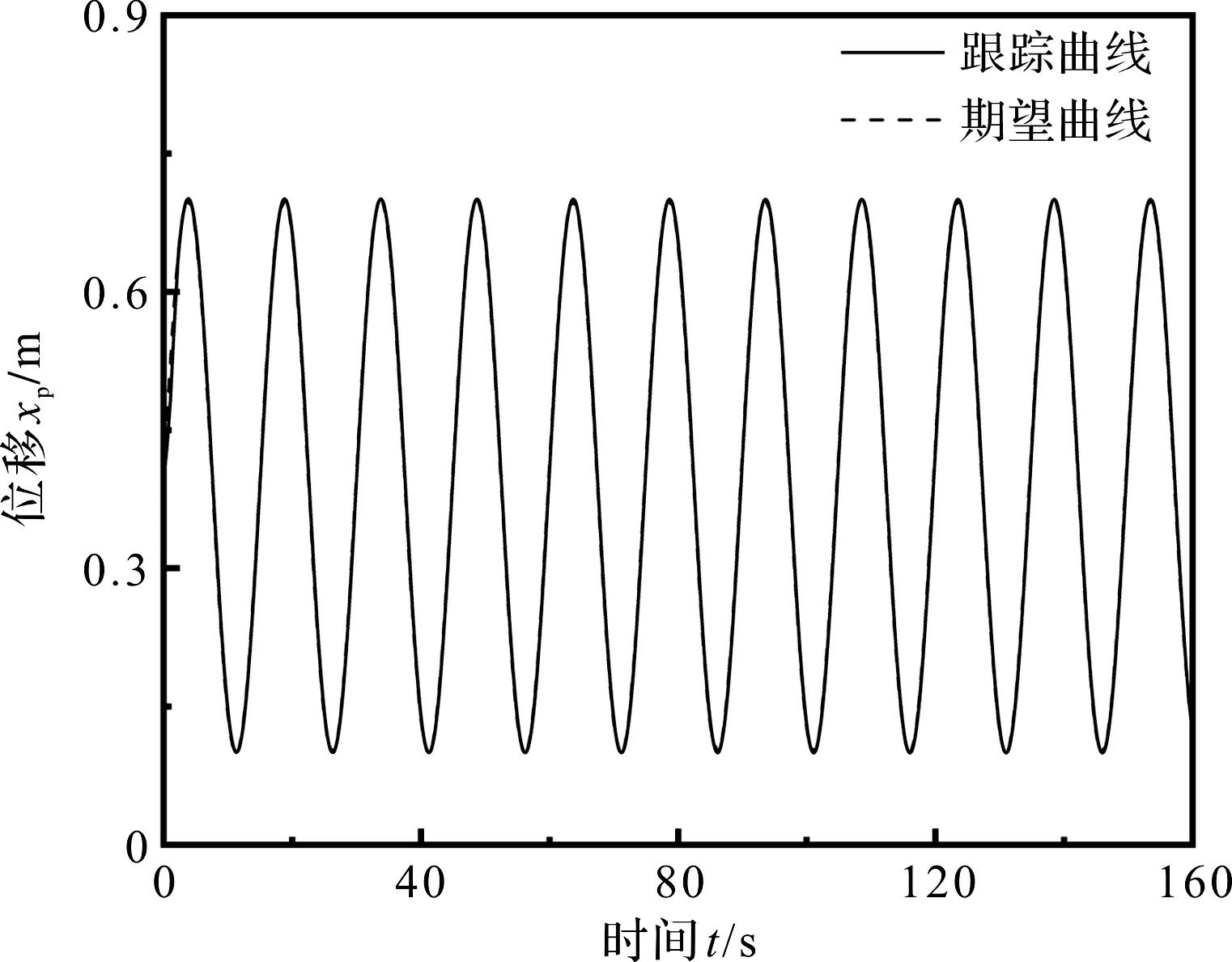
图9 加载位移图
加载位移局部放大图如图10所示。

图10 加载位移局部放大图
位移偏差图如图11所示。
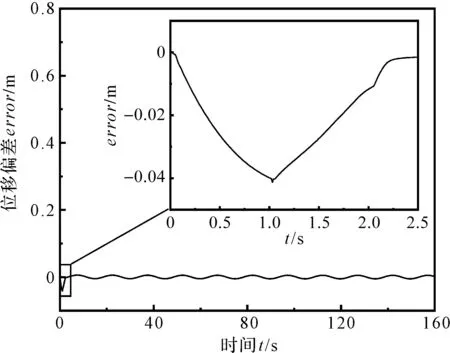
图11 位移偏差图
从图11的仿真结果可以看出:使用自适应模糊PID控制算法,通过AMEsim-Simulink联合仿真,在开始运动的2.5 s内偏差较大,之后跟踪曲线与期望曲线基本吻合,曲线跟踪效果良好;
最大误差发生在1.05 s时,数值为-41 mm;系统位移的稳态偏差维持在 -7.8 mm~5.7 mm,偏差范围为-2.6%~1.9%,完全在剪切位移的允许误差范围±5%之内;
期望曲线是正弦曲线,作动器在往复运动过程中存在加速和减速的阶段,因此系统稳态偏差有些许的波动。
位移-力滞回曲线如图12所示。
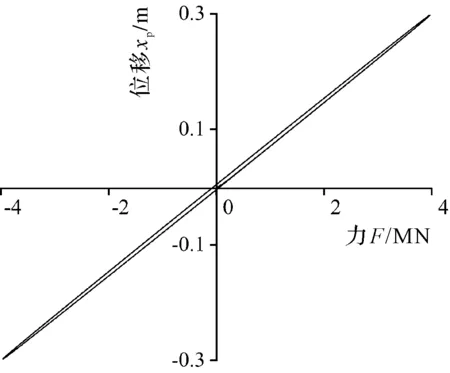
图12 位移-力滞回曲线
从图12可以看出:由于支座阻尼的存在, 位移与力的加载变化关系并不是通过原点一条直线,而是存在一定量的滞后。
4 结束语
为了解决压剪试验机水平剪切系统存在超大流量、超大输出力作用下的动态加载特性问题,笔者对压剪试验机的加载特性等方面进行了研究,并以电液比例位置控制系统为研究对象,采用自适应模糊PID控制应用于水平剪切比例位置控制系统中,研究结果表明:
(1)在自适应模糊PID控制下,系统达到稳态的时间较常规PID控制缩短了0.46 s;
(2)自适应模糊PID控制下,超调量由4.4%降至2.38%,震荡次数明显减少,系统的响应性得到了很好的优化;
(3)实际工况正弦加载下,稳态偏差在-2.6%~1.9%,位于剪切位移允许偏差±5%之内,符合系统的设计要求;
(4)得到了较好的系统位移-力滞回曲线,可为超大吨位压剪试验机的研制提供理论方面的指导。
在下一阶段,本研究将在压剪试验机制造完成后进行工程实际试验,进一步验证自适应模糊PID控制在超大流量、超大输出力水平剪切系统中的合理性以及控制精度特性等问题。
