电磁主动悬架作动器稳定性分析及特性试验

2019-09-27寇发荣李阳康杨慧杰

制造业自动化 2019年9期

寇发荣，李阳康，陈晨，孙凯，杨慧杰

KOU Fa-rong,LI Yang-kang,CHEN Chen,SUN Kai,YANG Hui-jie

（西安科技大学机械工程学院，西安 710054）

0 引言

悬架是现代汽车重要组成部分，关系到汽车的舒适性和操稳性[1]。汽车传统悬架是由弹性元件、液压减振器等组成，但由于其刚度和阻尼无法随路面以及汽车行驶状况而改变，限制了汽车性能的进一步提高[2～4]，目前主要采用主动悬架技术解决这一问题。针对主动悬架的研究主要集中在控制策略及控制算法[5～7]，对作动器结构研究较少。

文献[8,9]利用滚珠丝杠或齿轮齿条等中间传动装置将旋转运动转化为直线运动，但机构复杂且传动效率低。文献[10～12]利用电磁感应原理设计的电磁直线作动器，虽然结构简单，无需中间传动装置直接实现直线运动，但是存在气隙磁场密度低、占用空间较大、发热过多等缺点而无法正常使用。文献[13]通过改变电机的极距与齿槽距之比以及齿槽开口与齿槽距之比，得出这些参数对于齿槽力的主要谐波阶次以及幅值都有重要影响，但是对具体齿槽开口大小缺乏理论计算。文献[14]通过优化极弧系数和齿顶宽度进而削弱齿槽效应带来的法向力波动幅值，但忽略了对定子边端弧度以及作动器效率的分析。

在以上的研究基础上，设计一种12槽10极分数槽结构直线电机主动悬架作动器。通过反电动势的理论计算和力特性试验验证模型的正确性，考虑齿槽力和边端力的影响，进行理论计算和有限元仿真得出最佳槽口宽度以及定子边端弧度，并研究作动器的工作效率在不同电流下随三相电流频率变化规律，为下一步样机改进做基础。通过电磁主动悬架作动器的工作特性试验，分析作动器在不同的输入激励下的输出特性，以期为作动器整车装备提供参考。

1 电磁主动悬架作动器原理与结构设计

1.1 电磁主动悬架作动器原理

图1为电磁作动器及悬架安装结构示意图，其中直线电机作动器取代了普通减振器。当汽车行驶在不平度路面上，初级和次级铁芯在三相电流的激励下产生电磁推力抑制路面的冲击，从而提高汽车的平顺性与乘坐舒适性。

1.2 电磁主动悬架作动器结构设计

为了满足作动器的减振性能及占用装配空间小的要求，我们对作动器的外形尺寸进行如下要求：直线电机作动器初级外径小于85mm；作动器初级长度小于300mm；次级长度不小于500mm；气隙长度为1mm；采用分数槽结构和径向充磁；为了简化初级装配包括有绕组铁芯的装配[15]，选择作动器的初级外径和次级外径比值为2:1；结合整车装配尺寸的需要，槽型选择平底槽，槽宽等于12mm，槽数选择12槽，匹配的极对数如表1所示。

图1 电磁作动器及悬架安装结构示意图

表1 作动器极槽匹配

可以看出，12槽匹配的电机极对数有4，5，7。根据公式：2p=N±2，当极对数等于5和7时，会降低绕组中产生不同阶数的谐波磁电势，减小电磁力波动。文献[16]可知电机极数越多，产生的漏磁增加，而且同样速度下，铁损和驱动器开关损耗也会越大，进而降低电机使用寿命。因此该作动器的结构设计采用12槽10极，具体尺寸如表2所示。

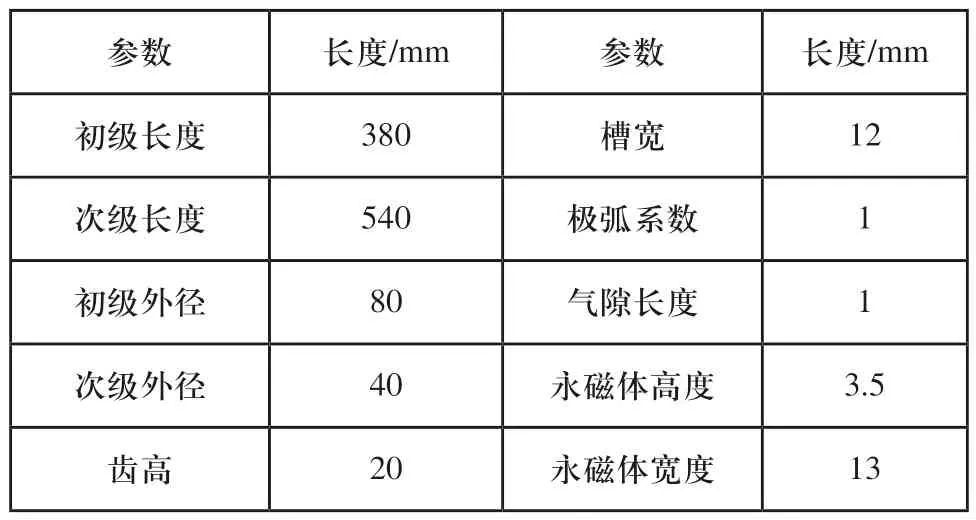
表2 作动器的主要结构参数

2 作动器有限元模型建立与验证

2.1 作动器有限元模型建立

依据作动器结构参数，在二维环境下建立作动器模型，因为直线电机作动器沿中心轴线对称，所以建模时只需建立沿Z轴对称的1/2模型，结果如图2所示。

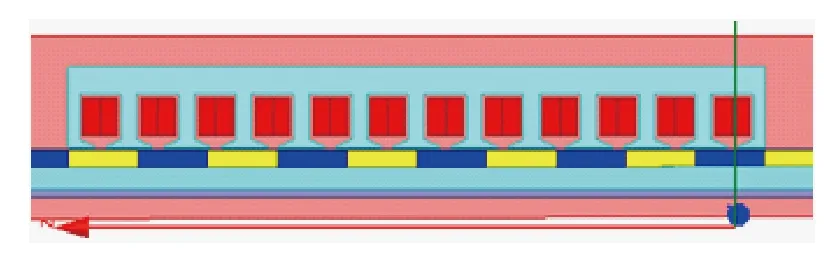
图2 有限元模型

为了得到较为精确的仿真结果，我们对作动器分析之前，将求解部分的网格划分的较密，图3为模型网格划分结果。

图3 网格划分模型

2.2 作动器模型的验证

2.2.1 反电动势计算

反电动势是作动器一个重要的参数指标，它的大小和正弦度直接影响电机的推力。本文通过理论计算和有限元仿真，对电机的反电动势作对比分析，并通过力特性试验证明所建立有限元模型的正确性，图4为作动器的机构尺寸示意图。

图4 作动器的结构尺寸示意图

所设计的作动器初级槽是开口结构，因此引入卡特系数：

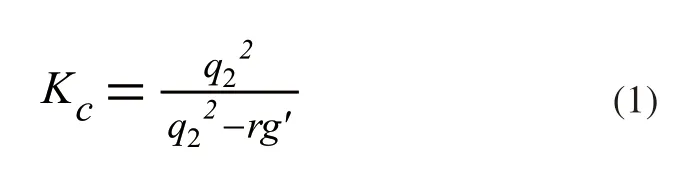
有效气隙为：

有效电枢厚度为：

（2n-1）次谐波系数为：

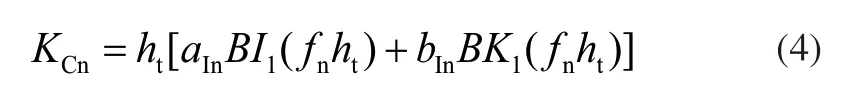
式中：fn为谐波的空间频率，fn=(2n-1)/。

ain和bin为一类和二类一阶贝塞尔函数BI1(.)和BK1(.)的系数。

单相绕组的反电动势为：

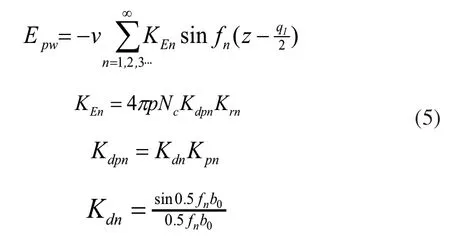
式中：v为作动器的运行速度；z=vt，为作动器的运行距离；NC为每极对应的绕组匝数；Kdpn为绕组系数；Kdn为分布系数；Kdp=1，为短距系数。

将作动器的运行速度定为1.3m/s，空载下分析反电动势Epw随时间t的变化，并与理论计算值作对比，结果如图5所示。

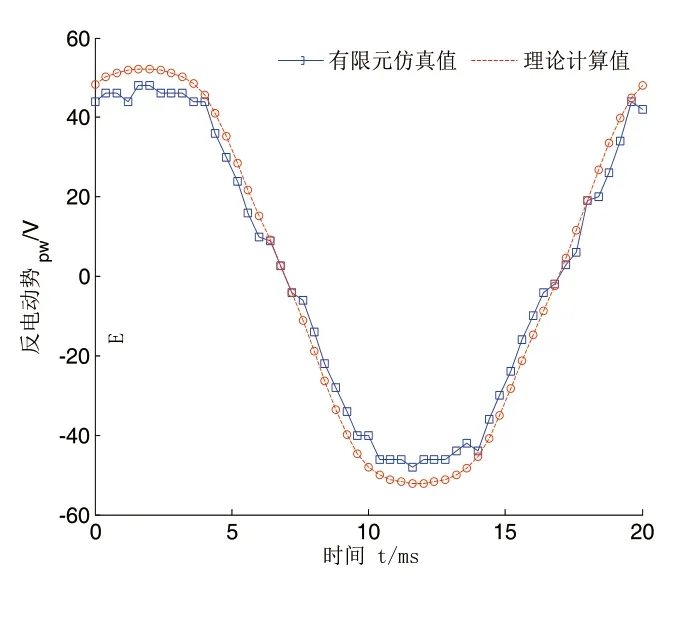
图5 单相线圈绕组的反电动势

由图5可知，作动器在空载条件下，一个周期反电动势的理论计算值与有限元仿真值吻合良好，且随时间的变化呈正弦波动。

2.2.2 作动器力特性试验

试制了作动器的样机，并展开了作动器力特性试验。试验仪器包括固定台、力传感器、TSGC2-6KVA型调压器、数据采集仪等，如图6所示。实验过程中，作动器的输入电压u从10V增加到50V，取电磁推力的平均值Ft并与仿真值进行对比，结果如图7所示。

图6 作动器力特性试验

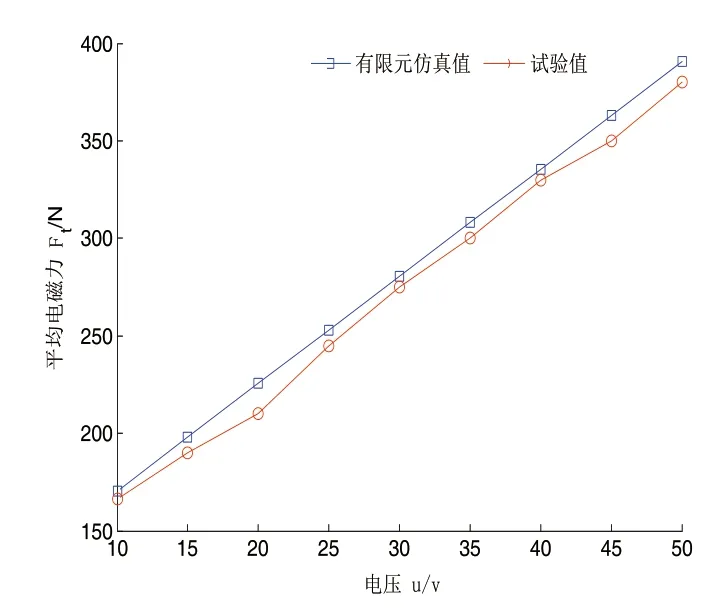
图7 平均电磁力随电压的变化

图7可以看出，平均电磁力的试验值和有限元仿真值基本一致，当输入电压为45V，两者误差值最大为6.2%。由此验证了作动器有限元模型的正确性。

3 作动器的稳定性分析

3.1 作动器的齿槽力分析

初级槽开口大小对电磁作动器的电磁推力和波动有较大影响，因为它决定了初级齿部极靴的宽度。通过理论计算和有限元仿真得到最佳槽口宽度，从而减小作动器齿槽效应对作动器波动的影响，提高直线电机主动悬架系统工作的精度。

为了便于分析，作以下假设：1）忽略作动器铁芯的涡流损失；2）初级齿的形状为长方形；3）初级和次级之间的气隙磁场为方波；4）永磁体磁导率与空气相同。

忽略铁芯饱和，作动器总磁场能量w可近似等于隙磁场的能量wgap，齿槽力为：

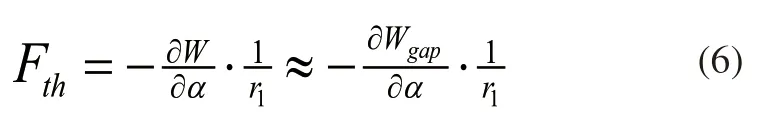
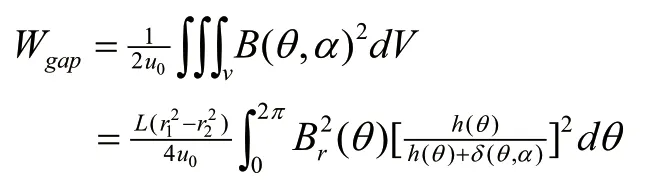
令：

式中：p为电磁作动器的极对数；z为作动器的槽数；GCD为最大公约数。

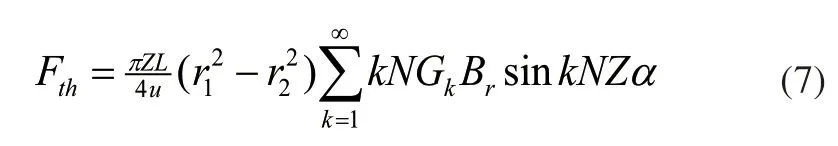
式中：Gk为相对气隙磁导平方的傅里叶分解系数；Br为永磁体产生气隙磁密平方的傅里叶分解系数。

通过合理选取槽口b0，可以使Gk尽可能接近零，以达到抑制齿槽力的效果。即：

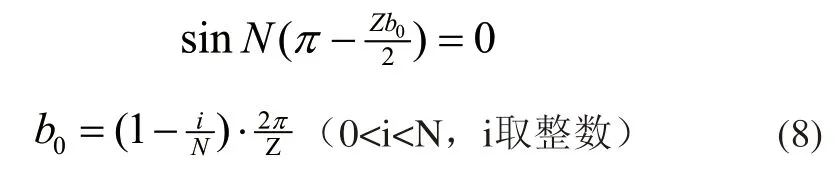
由此可得i取1，2，3，4；b0等于4.2mm，3.1mm，2.1mm，1.0mm。

根据理论计算的结果，作动器加载电压50V，次级运行速度为0.13m/s，改变槽口宽度，分析作动器的平均电磁力和波动比r的变化，仿真结果如图8所示。

图8 平均电磁力和波动比随齿槽开口的变化

由图8可知：槽口宽度等于4.3mm时，作动器的平均电磁推力最大为390.3N，此时作动器波动比最小为11.2%，波动力最小等于43.7N。这与通过解析式得到的结果相似，但是还存在一定的偏差。主要原因是解析法得到的结果，忽略了涡流现象和磁滞损失，且将气隙磁场假定为方波，这与作动器的实际运行状态存在一定的差距。

3.2 作动器的边端力分析

选择合适的初级长度可以有效减弱电磁作动器的边端效应，但边端力的产生是由于边端磁导的突变造成的。因此可以选择平滑的初级铁芯边端形状，耦合正弦气隙磁场，从而减小作动器的边端力，作动器的边端弧度结构如图9所示。

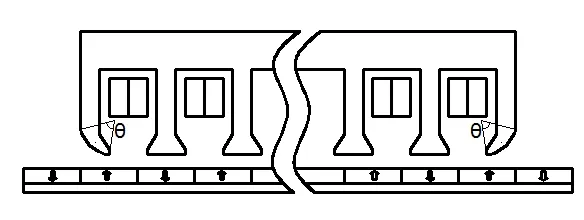
图9 作动器端部弧度结构图

改变边端弧度θ，作动器的仿真时间为300ms，次级速度设为0.13m/s，在空载条件下分析定位力随着时间的变化，结果如图10所示。

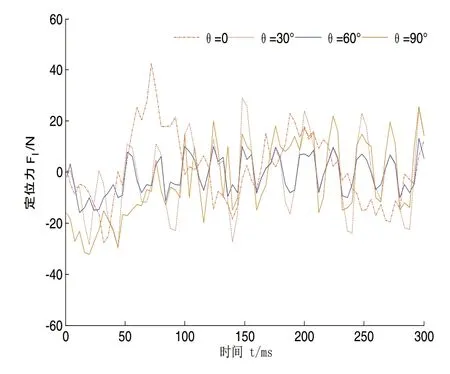
图10 不同形状边端的定位力随时间变化

由图10可知：当作动器的边端弧度等于60°时，定位力波动幅值随时间的变化最小，与原模型相比，定位力的波动幅值由21.4N减小到9.5N。

为了进一步分析作动器的电磁力变化情况，分别对改进边端弧度前后的作动器加载3.5A电流，次级速度设为0.13m/s，分析电磁力Fn随时间的变化规律，结果如图11所示，并进行数据计算，结果如表3所示。

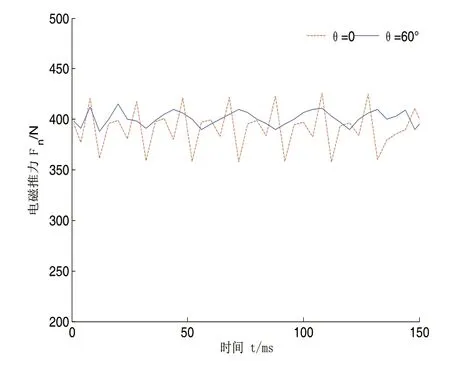
图11 电磁力随时间的变化

表3 波动力减小参数

通过图11和表3可知：改进前作动器加载电流波动值等于41.2N，通过改进边端弧度，减小了25.5N，差值比为61.9%。空载下的作动器定位力由21.4N，减小到9.5N，差值比为55.6%。此外还可以得出，定位力是电磁力波动的主要来源。

3.3 作动器的效率分析

作动器的效率是衡量直线电机输出能力和稳定性重要的指标。忽略机械能的损失，作动器能量的消耗主要包括有效功率、线圈绕组的热损耗以及其他损耗。作动器的计算方式用以下公式：

式中：η为作动器效率；Pe为输出功率；Ps为输入功率；Ft为平均电磁推力；V为作动器的速度；τ为永磁体长度；f为三相交流电的频率；U为输入电压；I为输入电流。

仿真分析作动器的平均电磁推力和效率在不同电流下随三相交流电频率变化规律，如图12所示。

由图12可知，作动器的平均电磁推力随电流的增大而增大，随着三相电流频率的增大而减小，作动器推力在低电流高频率下的最小值为168N，在高电流低频率下的最大值为759N；作动器效率随着电流的增大而降低，随着频率的增大而提高，在高电流低频率下效率最低为5.1%，在低电流高频率下效率最高为86.7%。

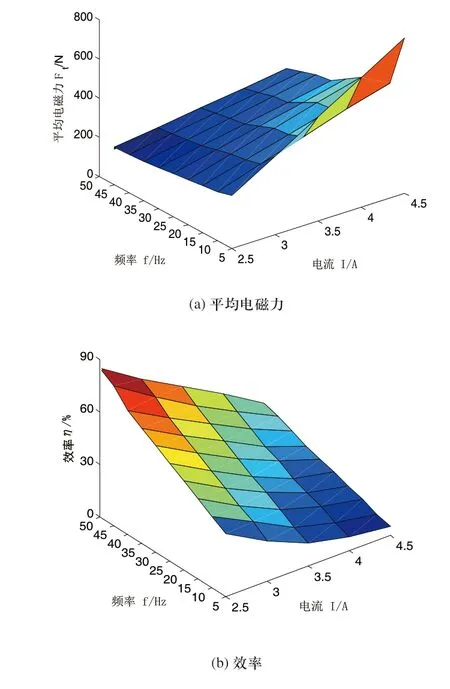
图12 作动器的平均电磁力和效率

4 电磁主动悬架作动器工作特性试验

汽车行驶在不同路面条件下，电磁作动器输出电磁推力，用于衰减来自路面的激励。为了满足悬架的减振要求，作动器的工作应满足功能设计需要。将电磁作动器安装在悬架试验台上，电磁作动器的下端与试验台下横梁相连，下横梁与电磁振动台连接，电磁作动器的上端与上横梁连接，上横梁放有配重块，用于模拟汽车簧上质量，如图13所示。电磁振动台输入不同速度的激励，分别测试不同振动速度下作动器的输入电源激励和输出特性，试验结果如表4所示。

图13 电磁作动器试验

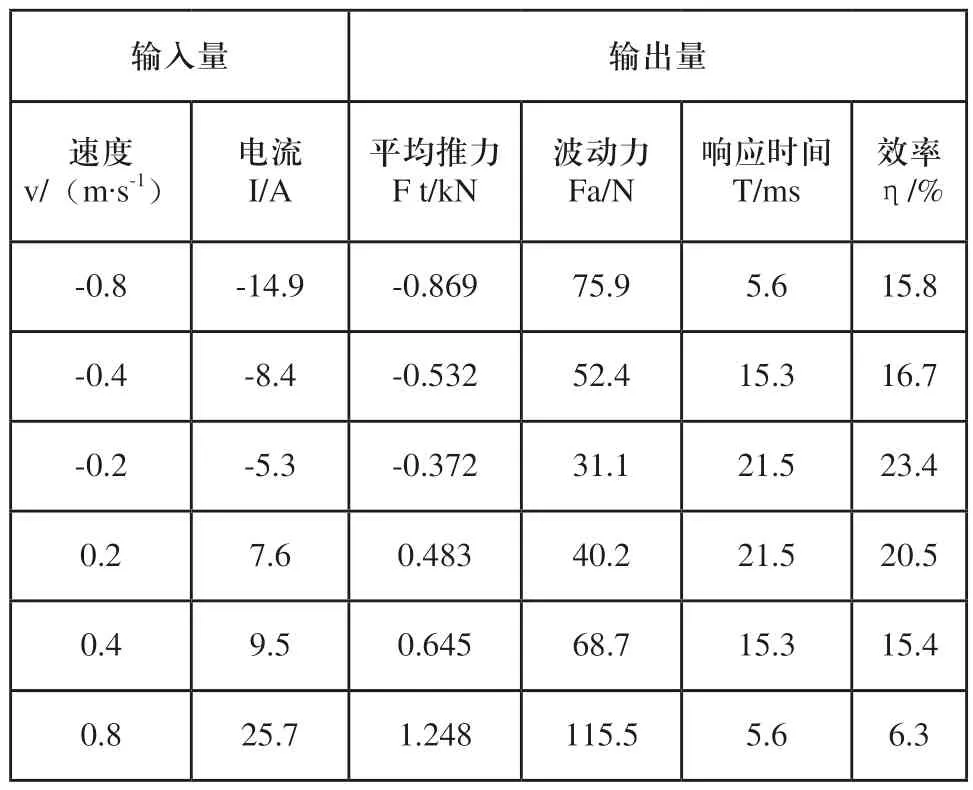
表4 不同速度下电磁作动器的输入和输出的特性参数

由表4可得：随着悬架振动台的速度提高，所需电磁作动器的推力也越大。当作动器的加载电流增大时，电磁作动器作动器的波动力Fa不断变大，响应时间T缩短，工作效率降低。为了满足悬架减振性能的要求，随着悬架运行速度的变大，应逐渐增大电磁作动器作动器的激励电流的幅值。此外根据v=2τf，也应增加三相电流的频率。