导引头电子舱框架有限元仿真及模态试验

陆 玥, 刘亚龙, 刘 宇, 张发洋

(上海无线电设备研究所,上海201109)

0 引言

导引头电子舱在导弹飞行过程中,会受到发动机及气动力矩的受迫振动、各种冲击、过载效应和噪声干扰的综合作用,始终处于复杂激励状态。随着导引头朝向小型化、轻量化的方向发展[1],要求结构件更加轻薄。随之带来电子舱结构强度下降,振动量级过大等问题,可能会导致产品工作异常。同时,随着相控阵技术的应用和复合体制导引头的普及,导引头结构发生了较大改变。传统的经验设计参考价值不高,需要对新体制的导引头进行细致的力学分析,保证结构设计的可靠性[2]。

模态特征能够从质量和刚度特性上反映结构的力学性能。采用仿真或试验的方法对产品进行模态分析,可以清楚了解结构在某一易受影响频率范围内的各阶主要模态特性,为结构系统的振动特性分析、振动故障诊断以及结构动力特性的优化设计提供依据。其中有限元模态仿真分析灵活便捷,可以快速得出模态振型,用以指导模态试验力锤激励点位置排布。但是仿真结果依赖仿真工程师经验,难以一次性保证仿真置信度。试验模态分析可以直观地显示结构的动力学特性,得到的低阶模态固有频率和模态振型结果非常可靠。但是模态试验对试验条件有一定要求,大型结构的模态试验时间较长。对复杂结构进行模态试验[3-4]是结构动力学设计中必要的环节。同时,使用模态试验得到的参数对有限元仿真模型进行修正,是建立足够精确的有限元模型的重要手段[5-7]。本文对某导引头电子舱框架结构进行有限元模态仿真分析及模态试验,分别得到电子舱框架的固有频率和振型,并进行比较,验证仿真分析的可靠性。

1 模态分析原理

模态分析的主要目的是分析系统的固有特性,从而确定模型的固有频率和相应振型。假定在无激励无阻尼的作用下,模型的振动方程为

式中:M为质量矩阵;K为刚度矩阵;为节点速度矩阵;u为节点位移矩阵。可将模型变为简谐运动,令ω为角频率,u=u(t)ejω t。求解可以得到ω的多个解,任意一个解代入u可以得到相应位移变化矩阵,进而得到模型固有振型。

真实情况下模型会有阻尼,并且存在外部激励。此时的线性微分方程为

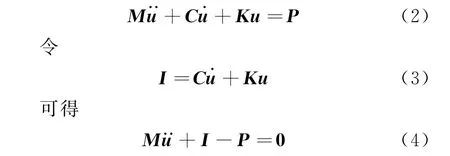
式中:m、k和c分别表示系统的质量、刚度与阻尼。而对于n输入和n输出的线性时不变多自由度系统(n≥2),它的频率响应函数为一常数矩阵,表示为

式(6)中的任一元素Hl p的表达式为

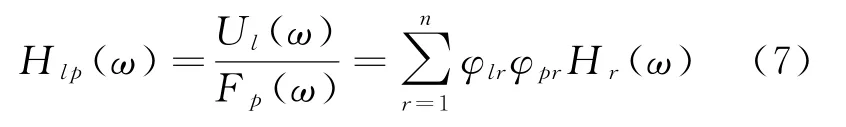
式中:l为响应点自由度;p为激励作用点自由度;φ表示振型函数;Hl p表示在p自由度上作用单位力时,在l自由度上所引起的响应,即l和p两点之间的频响函数。

2 电子舱框架结构模态仿真

2.1 仿真模型的建立及网格划分

将在Pro/E三维软件中建立的导引头电子舱框架几何模型导入到网格划分软件Hyper Mesh中进行有限元仿真分析。在分析过程中,需要对模型进行适当的简化处理。由于在仿真中没有使用到的螺纹孔对模态影响极小,同时较小的孔处理不当可能会导致网格畸形,影响计算结果,因此对其进行几何清理。本文采用Hyper Mesh四面体网格划分功能,对螺纹孔等特征较为密集的地方进行细化处理,其他部分网格较为稀疏。划分结果如图1所示。该处理方法可以极大地提高计算效率,同时也可以保证计算精度。

图1 导引头电子舱框架有限元网格划分

2.2 材料属性设置

电子舱框架包含连接环、梁、底板及紧固件。其中连接环、梁和底板材料为铝合金(2A14),螺栓为不锈钢(1Cr18Ni9Ti)。各材料属性见表1。

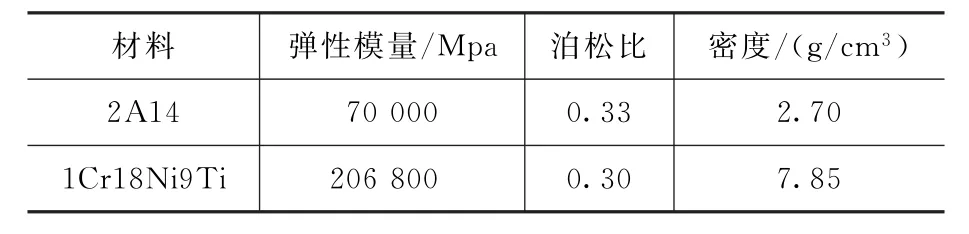
表1 模型材料属性

2.3 螺栓连接等效方法

结构件之间经常使用螺栓进行连接和固定,各结构件连接处的处理方式对有限元仿真精度的影响极大[8]。如果根据实际结构建立仿真模型,会使模型边缘复杂、结构自由度增加,导致网格划分困难、计算时间增加,甚至产生仿真结果不收敛问题,导致仿真计算失败[9]。在结构分析中,很多时候只需考虑结构整体性能,通过对模型和连接方式进行简化处理,将复杂的结构形式进行等效,便于网格的优化,加快计算速度。

Hyper Mesh中提供了强大的一维单元创建功能,可以简化并等效螺栓连接、焊接和粘接等常用的连接方式,用户可以根据自己的模拟需要选择不同的一维单元。本文使用梁截面工具Hyper Beam创建刚性(rbe2)单元。rbe2单元是一种模拟多节点自由度耦合关系的单元,可以用来模拟刚度非常大的构件,如螺栓与结构件的螺纹连接。如图2所示,rbe2单元将螺纹孔中的网格节点进行刚性抓取,将螺纹孔的刚度集中在一点上,以代替两端的螺纹连接。杆(bar)柔性单元可以用来模拟螺栓的螺杆等一个方向尺寸远大于另外两个方向的构件。如图3所示,使用bar单元分别连接两个rbe2单元的集中点,同时定义bar单元的横截面积和材料参数。由此bar单元和rbe2单元就可以组合成为一种简化螺栓的连接方式。螺栓连接的整体等效方式如图4所示。

图2 rbe2单元等效螺栓的螺纹

图3 bar单元连接方式

2.4 模态仿真结果

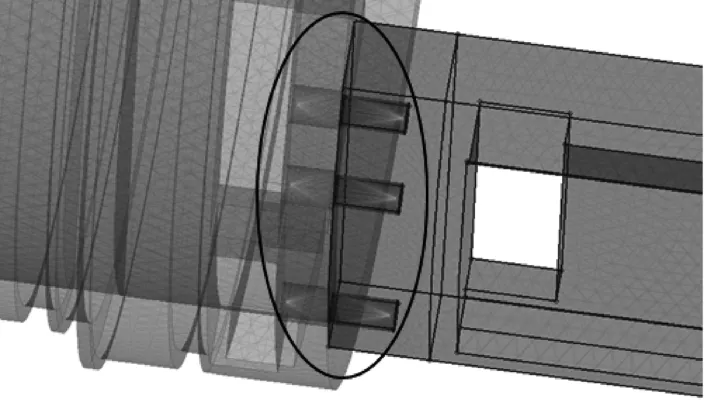
图4 螺栓连接等效方式

利用Nastran软件分析上述模型的自由振动模态,即自由状态下结构振动特性,得到400Hz以内的固有频率依次为120.1,173.6,249.3,339.8Hz,对应振型如图5所示。其中1阶为整体横向的同侧弯曲变形,2阶为整体纵向的异侧弯曲变形,3阶为梁横向的异侧弯曲变形,4阶为梁横向的同侧弯曲变形。

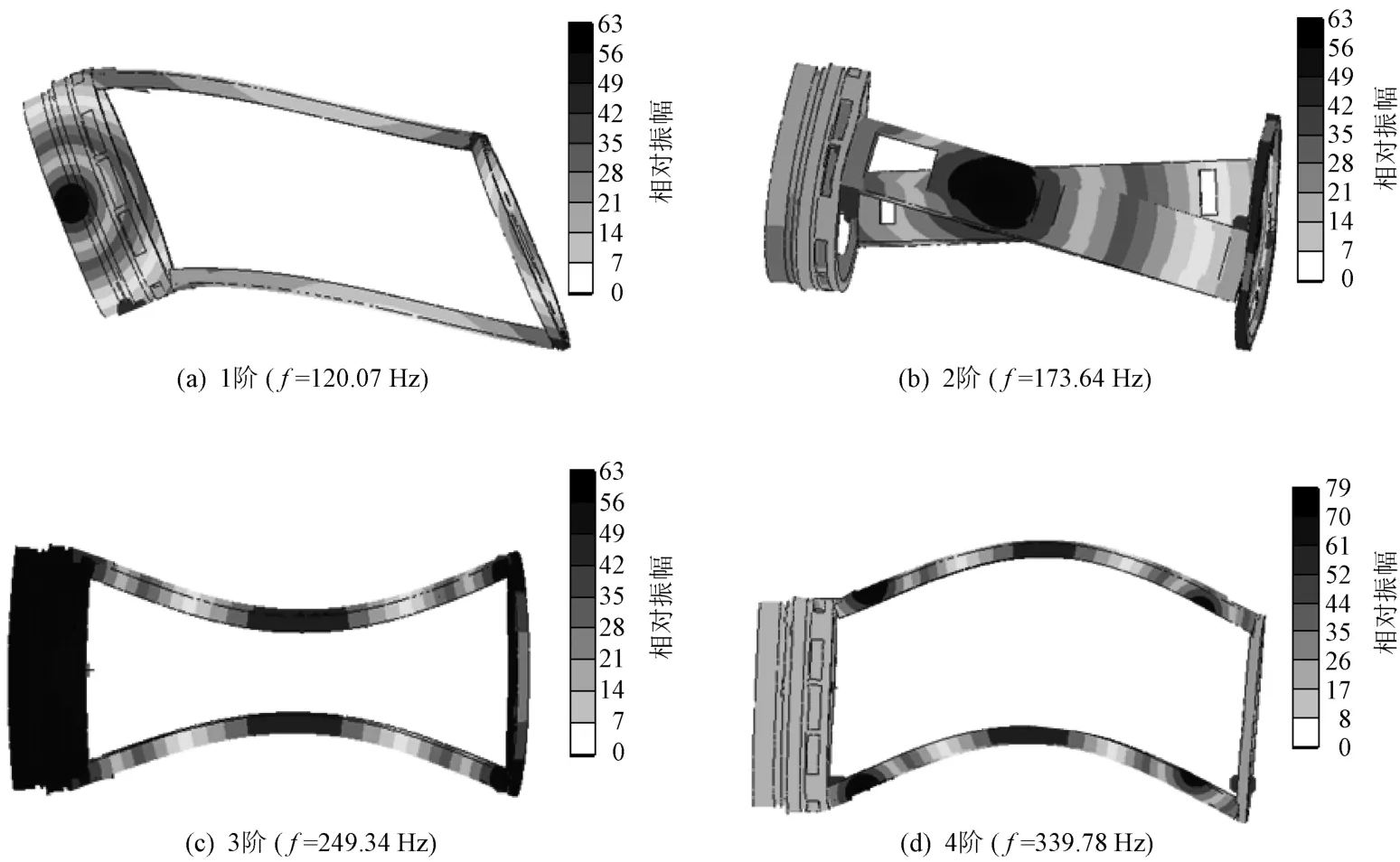
图5 仿真振型

3 电子舱框架结构模态试验

模态试验可以从实际结构的激励和响应数据中辨识结构的数学模型和特性参数。工程应用中,可以用模态试验的结果验证和修正仿真模型,校核动态分析结果的有效性,检查结构中的薄弱点及鉴定结构的动态特性是否符合设计要求。

3.1 试验方案

模态试验采用的主要设备有东华DH 5902信号采集处理系统、安装江苏东华模态分析软件的计算机、B&K公司三轴向加速度传感器、力锤。

进行模态试验前,需要在模态分析软件中建立试验模型。通过仿真得到的振型确定节点位置,并在电子舱框架结构上标出与试验模型节点对应的激励点,作为力锤敲击的位置。本次试验采用跑锤法进行激励,即使用力锤敲击不同激励点,传感器位置不改变,采集各点的频响函数进行模态识别。试验模型如图6所示。

图6 试验模型

模态试验分析关键步骤包括施加激励、参数采集、参数识别等。为了获得所关注频率范围内的所有模态振型,应该合理地选择激励点与响应点,并完成相关参数的设置。为了更好地模拟导引头电子舱框架的工作环境,排除外界物体振动对框架的干扰与影响,本试验采用弹性细绳悬挂的方式来模拟自由边界条件。

测试系统框图如图7所示。将电子舱框架悬吊好后,贴好加速度传感器,打开信号采集处理系统,设置好相应参数。使用力锤敲击框架上标记好的激励点,为保证精确度,每个点敲击四次进行平均。待所有点都敲击完成后,使用模态分析软件对采集到的数据进行处理,即可得到模态频率及其对应的振型。

图7 试验测试系统框图

3.2 试验结果及对比分析

通过对试验数据进行分析、处理,识别模态参数,得到400Hz以内的试验振型如图8所示。模态试验得到的被测件固有频率依次为125.6,177.5,230.1,325.1Hz,各频率对应的振型与有限元仿真结果一致。

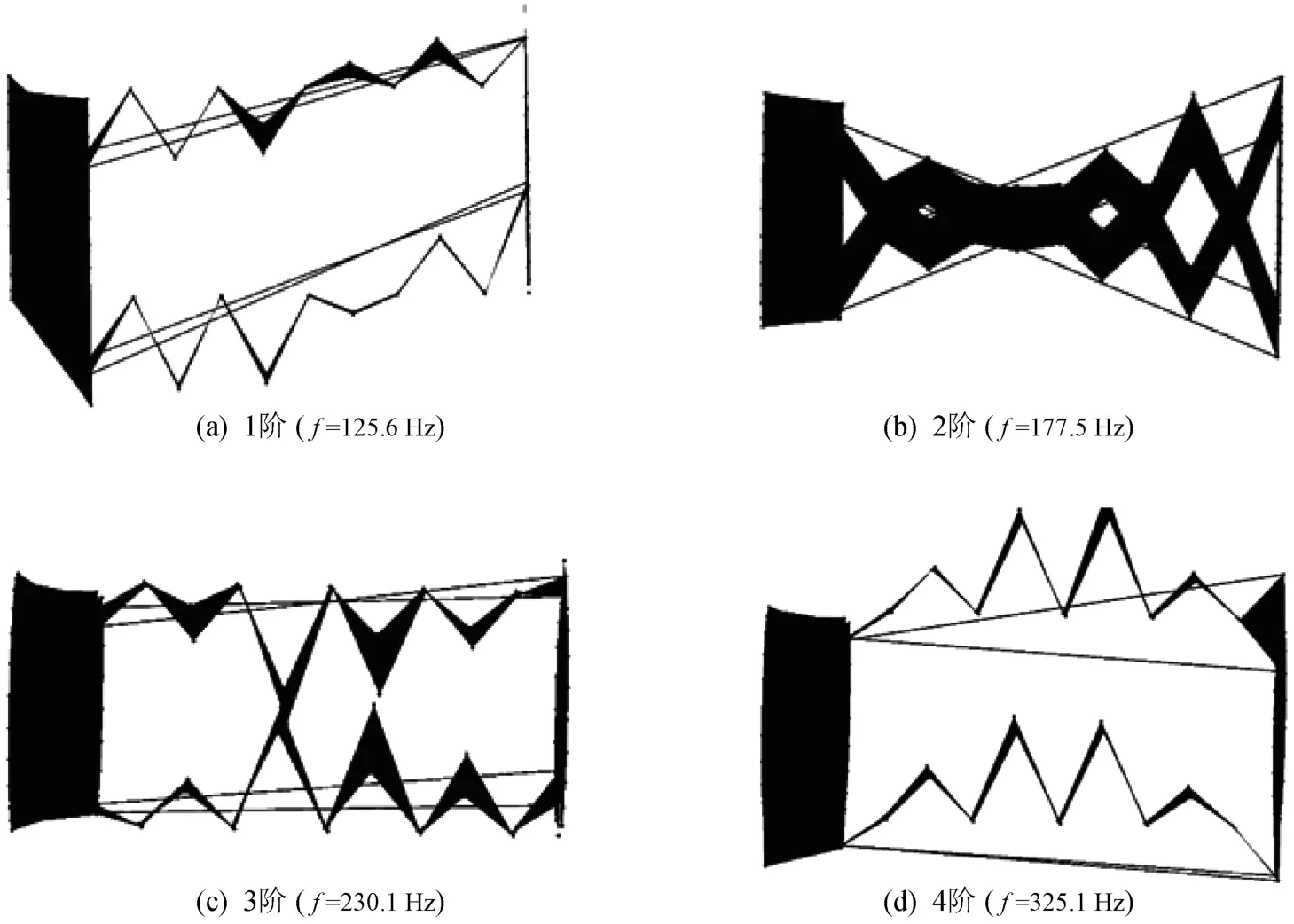
图8 试验振型

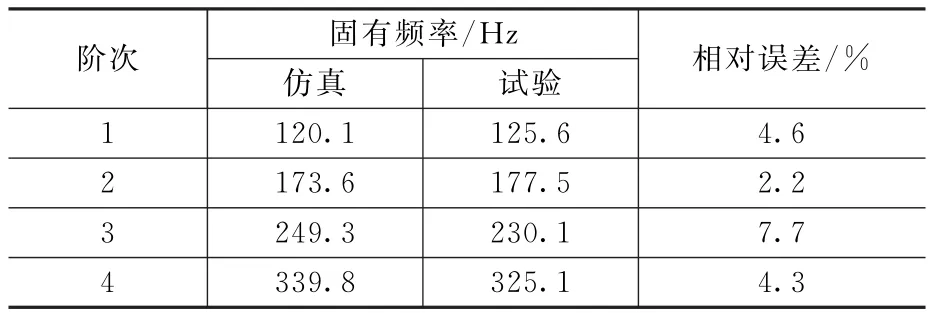
表2 有限元仿真与试验获得的固有频率对比

综合对比试验结果和有限元仿真结果,二者所得固有频率对比如表2所示,仿真与试验所得固有频率在数值上最大相对误差为7.7%。经分析初步判定,二者不一致的主要原因包括:a)试验中被测件螺栓连接处结构较为复杂,与有限元中简化的结构相比,质量更大;b)试验中通过细绳悬挂框架来模拟自由边界条件,绳子具有一定刚度,不能完美复现有限元仿真中的自由状态;c)传感器等增加了试验中被测件的质量;d)力锤激励、采集电缆以及人为操作导致试验结果存在误差。但是通过对比振型可以看出,试验所得振型与有限元仿真中所得振型完全符合,因此仿真结果较为准确。

4 结论

本文建立了导引头电子舱框架结构模型,并提出了一种螺栓等效方法,进行了有限元模态仿真,得到其400Hz以内固有频率及模态振型。通过力锤激励方法对该结构进行了模态试验,并与仿真结果进行对比,试验测得的固有频率与仿真结果相对误差均在10%以内,并且模态振型完全一致,验证了仿真结果的准确性。在后续结构设计中,可用该仿真方法进行结构强度与刚度校核。