基于犹豫模糊集的特征辅助数据关联算法
2020-12-23朱嘉颖王雪博李俊山袁鹏程张韬杰
朱嘉颖, 王雪博, 李俊山, 袁鹏程, 张韬杰
(上海无线电设备研究所,上海201109)
0 引言
在日益复杂的电磁环境下,国土防空面临着异常严峻的形势。国土防空警戒系统作为战场上的千里眼,担负着保卫国土的第一重任,开展空中多目标实时跟踪技术研究显得尤为重要。数据关联是一种在多目标实时跟踪过程中十分关键的技术。概率数据关联(Probabilistic Data Association,PDA)算法[1]和联合概率数据关联(Joint Probabilistic Data Association,JPDA)算法是两种最常用的传统关联算法[2],二者均利用雷达获得的目标位置信息实现点迹-航迹关联。其中PDA算法主要适用于单目标跟踪。而JPDA算法是专门针对多目标跟踪问题提出的,但在近距分布的量测数和目标数增加时,JPDA的算法复杂度呈指数增长,会引发“组合爆炸”现象。针对传统算法的局限性,近几年也有一些改进算法被提出。ZENG等[3]提出一种基于贝叶斯检测的杂波下目标跟踪数据关联算法。WU[4]提出改进的交互多模型概率数据关联算法实现对机动目标跟踪。陈晓等[5]在数据关联算法中引入概率加权概念来提高关联性能。事实上,随着各种传感器的迅速发展,雷达可获得的目标特征信息越来越丰富,如幅度特征、频率特征、重频特征和目标距离像特征等,如何利用这些特征来辅助数据关联过程并提高数据关联准确度正是本文要讨论的。王杰贵[6]提出利用灰关联思想简化数据关联过程,提高了算法实时性。郑浩[7]提出结合多种特征信息,利用证据理论对联合数据关联算法进行改进。李为[8]提出用目标信号幅值辅助概率数据关联的算法。2017年,孙启臣等[9]提出一种基于灰关联证据距离法的数据关联方法以提高数据关联准确度,但在目标和杂波密集的情况下,该方法的实时性较差。王树亮等[10]结合人类视觉注意机制,提出一种适用于认知雷达[11-12]的数据关联算法。本文结合犹豫模糊集思想,对现有基于灰关联的特征辅助数据关联算法进行改进,提出一种适用于非线性多目标跟踪的数据关联新方法,并通过仿真验证该算法的有效性和优越性。
1 非线性多目标跟踪
1.1 非线性多目标跟踪原理
非线性多目标跟踪的根本任务是,将从监视空域获取的量测信息转化为各种不确定机动目标的相应轨迹信息,从而实时掌握该区域内各机动目标的运动状态,为后续战场态势评估提供基础支持。
非线性多目标跟踪实际上是一个递推过程,基本原理如图1所示。首先为满足跟踪起始逻辑的目标创建新的航迹档案。在之后的每个采样时刻,对获取的量测信息按照跟踪门规则进行归属性判决,只有落入目标跟踪门内的量测才可能被用来更新目标航迹,并通过数据关联规则来实现量测和各条航迹的相互匹配[13]。然后利用关联成功的量测-目标对信息,采用自适应滤波与预测等跟踪维持方法更新各条已建立的航迹。当有目标满足跟踪终止逻辑(离开监视空域或被摧毁)时,则消除其目标档案。最后在下一采样时刻之前,由目标预测状态和估计误差协方差确定新的跟踪门中心和大小,并继续进行递推循环。
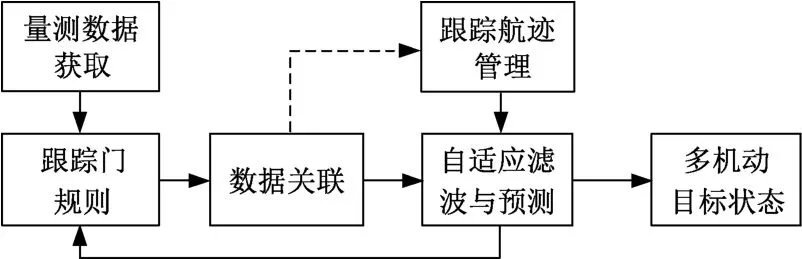
图1 非线性多目标跟踪基本原理
数据关联技术在非线性目标跟踪中发挥着举足轻重的作用。特别是在复杂电磁环境下对多目标进行跟踪时,由于缺乏跟踪环境的先验知识且受探测设备性能的制约,回波量测与其目标源之间的对应关系被破坏,必须运用数据关联技术来寻求解决之法。卡尔曼滤波为公认运行最快且性能最稳定的滤波算法之一,而卡尔曼滤波跟踪理论也成为了目前应用最广泛且发展最成熟的跟踪理论。本文提出的数据关联新方法就是基于非线性卡尔曼滤波跟踪算法体系的。
1.2 概率数据关联算法
PDA算法假设在被监视空域内仅有一个目标,且其航迹已形成,主要关注量测与现有航迹之间的关联问题,以及航迹维持和更新问题。但在杂波和噪声密集环境下,任一采样时刻获取的有效回波可能不止一个,PDA理论认为它们源于目标的概率是不同的。
PDA算法中最关键的当属对关联概率β的确定。假设t时刻确认量测个数为mt,用表示在t时刻第i个量测zt,i来自目标这一事件的概率,则
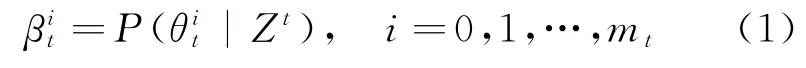
式中:Zt表示直到时刻t的累积确认量测集。当i=0时,表示没有量测源于目标的概率,从而有假设虚警量测数服从参数为λ Vt的泊松分布,其中,λ表示杂波密度,Vt表示跟踪门的体积。可计算得到

1.3 基于犹豫模糊集的特征辅助数据关联算法
JPDA算法是在PDA算法的基础上,为解决多目标跟踪问题而提出的,该算法具有优良的相关性能,得到了广泛应用。而该算法对联合事件概率的遍历性计算,使得计算负荷随回波密度的增大而呈指数级增长,严重降低了目标跟踪实时性。
随着无源探测技术的飞速发展,可获取的雷达信息越来越丰富,特征辅助数据关联算法就是要利用位置信息之外的其他特征辅助目标跟踪过程,以提高多目标跟踪的精确性和实时性。本文选取脉冲重复周期T,脉冲宽度τ,载频f三个特征参数辅助基于位置信息S的关联过程,为适应不同应用场景也可选取其他辅助参数。模糊集是一种用来表征事物模糊性和不确定性的理论,但由于决策环境的多变性,在确定合适的模糊数来对复杂问题进行评价和决策时,易出现摇摆不定、犹豫不决的情况。而犹豫模糊集允许某元素对集合的隶属度为几个可能的值,以解决上述问题。不同信号类型下,各特征下的关联程度求取方式存在差异。为防止这种差异带来额外误差,同时为了最大限度保留贝叶斯最优估计特性,本算法先利用犹豫模糊集理论对落入多目标门限交叉区域而导致关联判别存在歧义的量测进行处理,对多种信号类型下对应的关联度进行融合处理,再将其按概率分配给各个目标,最后结合PDA算法进行目标跟踪。
在极坐标系下,假设在采样时刻t从目标空域获取的所有位置信息St的量测Zt=(ρt,θt),相应特征参数信息Ct=(Tt,τt,ft)。
在t时刻各目标航迹预测值周围设定扇形跟踪门,以此来判定所有量测的有效性。若则第j个量测为目标i的有效量测。其中,ρg]a]t]e,i和θg]a]t]e,i分别为目标i在极坐标下的两个跟踪门门限值分量。
所有有效量测中同时落入多个目标跟踪门交叉区域内的量测称为公共量测。假设在t时刻,共有Ns个公共量测,而第js个公共量测落入了Mjs个目标跟踪门的交叉区域,可能关联第is个目标。其中,js∈ {1,2,…,Ns},is∈ {1,2,…,Mjs}。下面针对第js个公共量测和第is个目标进行介绍。
基于获取的公共量测向量Zt(js)=(ρt,js,θt,js)和特征向量Ct(js)=(Tt,js,τt,js,ft,js),求取各种雷达信号类型下该公共量测与各目标的关联度[7]。引入犹豫模糊集思想,将求得的不同类型、不同特征参数表征的公共量测与各目标关联程度数据进行整理,建立犹豫模糊决策矩阵Xjs,表达式为
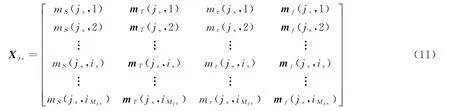
式中:mS为位置状态关联因子;mT=(mT,1,mT,2)为重频周期关联因子;mτ为脉冲宽度关联因子;mf=(mf,1,mf,2,mf,3)为工作频率关联因子。具体含义如表1所示。
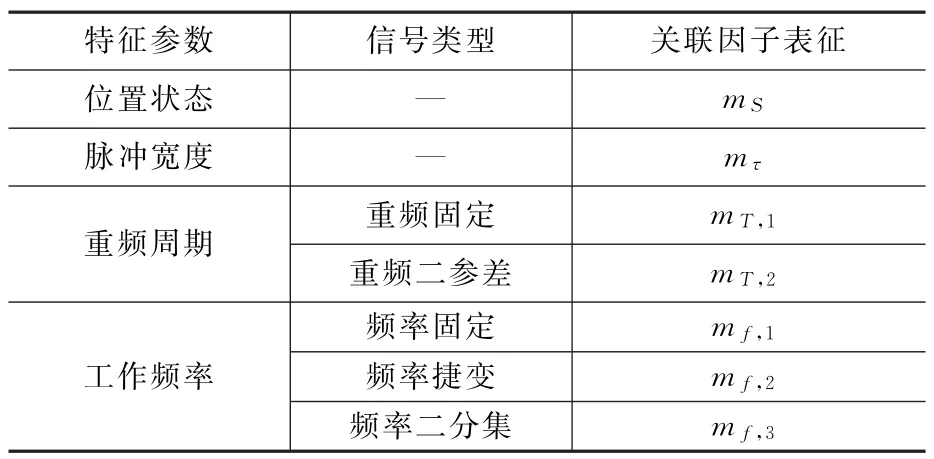
表1 不同特征参数的关联因子表征

由于Xjs内各数据均为效益型[14],因此规范决策矩阵Rjs=Xjs。若犹豫模糊元h的长度为L,且hi(i=1,2,…,L)为离散灰模糊数,则称为犹豫模糊元h的核。将Rjs转换为核与上下偏离值的决策矩阵,并形成参考数列
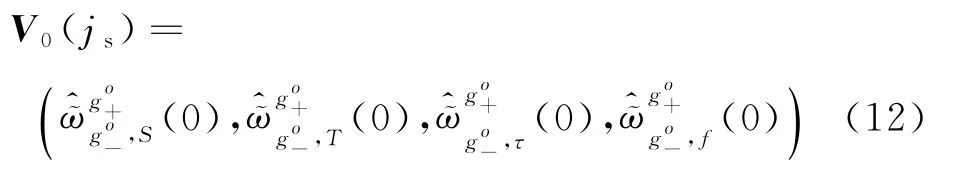
根据参考数列和决策矩阵,得到灰关联系数ζjs,k(is)和灰色关联度γjs(k)分别为
则各特征属性的权重值
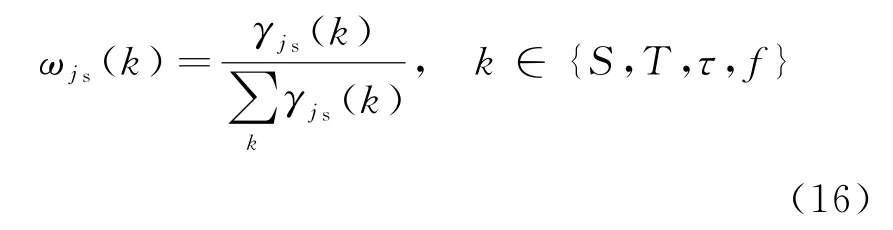
根据得到的权重值,确定加权综合属性值
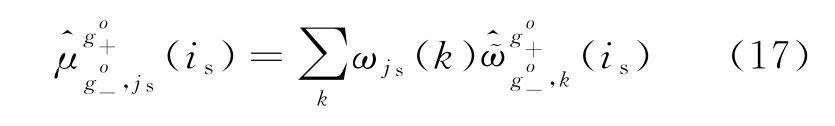
根据灰度不减公理[15],的灰度等于参与运算所有灰数的灰度最大值,而不会降低或减少。
将可能关联目标的加权综合属性值还原为常规灰数形式,表达式为
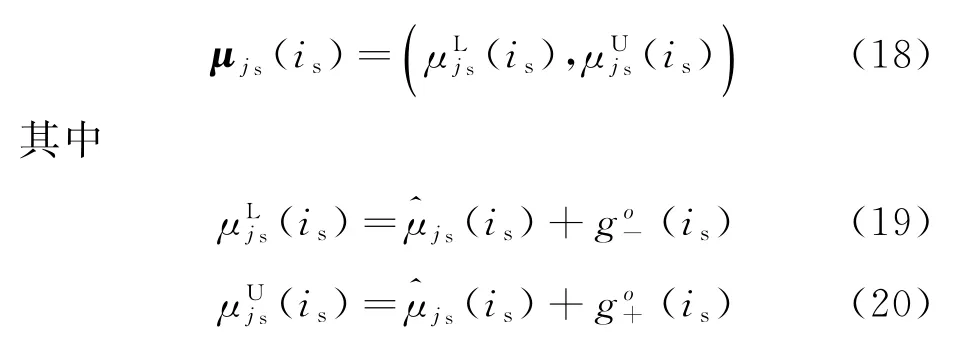
式中:μjs(is)为区间灰数;为灰度区间下限;为灰度区间上限。对所有可能与第js个公共量测关联的目标进行比较并求取各自可能度[16],表达式为
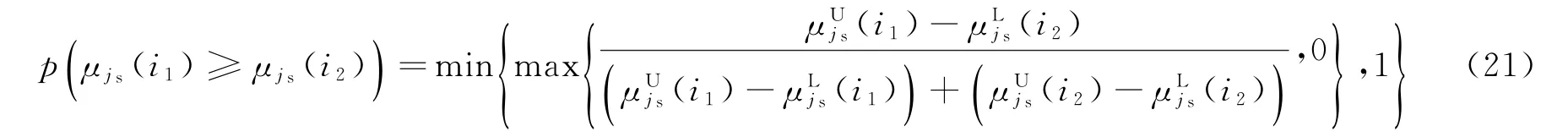
令rjs(i1,i2)=p(μjs(i1)≥μjs(i2)),可以得到排序向量ujs=[ujs(1)ujs(2)…ujs(Mjs)]T。其中
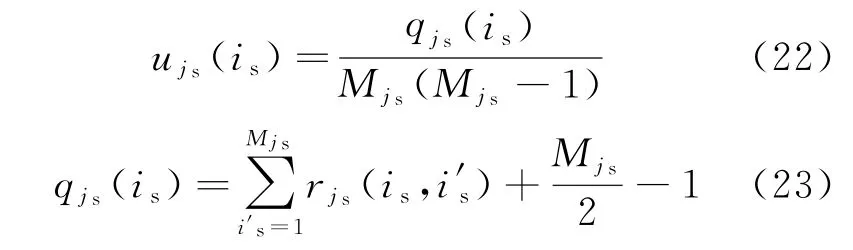
求取公共量测与对各个目标的分配概率矩阵Y,有
式中:js和is为量测j和目标i在Y中对应的位置坐标;α>0为比例调节因子,一般取α=1。
利用分配概率对各目标与跟踪门内量测的关联概率进行修正,修正矩阵Fc为对分配概率矩阵Y的扩展,则

修正后的关联概率


2 非线性多目标跟踪仿真
2.1 仿真误差计算
设置5个目标在杂波环境下做近距离小角度交叉非线性运动,利用多种数据关联算法对目标进行跟踪仿真。
为了便于区分,以下将基于灰关联的特征辅助数据关联算法[6]记为GRDA算法,基于灰关联证据距离法的特征辅助数据关联算法[7]记为GREDDA算法,基于犹豫模糊集的特征辅助数据关联算法记为HFS-DA算法。仿真主要考察的算法性能指标为跟踪成功次数和距离平均相对误差。
(1)跟踪成功次数
在非线性跟踪过程中,由于模型局限性和杂波环境的不确定性,偶尔会出现跟踪误差较大的情况。本文通过平均相对误差δf来表征平均每次跟踪的整体精度,其计算公式为
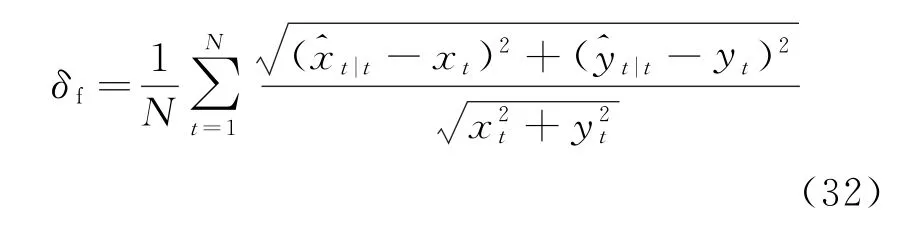
式中:N为采样点数;(xt,yt)为t时刻目标真实位置信息;为t时刻目标位置估计值。某次跟踪仿真所得的δf低于门限值时,则认为目标跟踪成功,门限值可根据实际精度要求设定。进行蒙特卡洛实验并统计跟踪成功次数Ms]u]c,用于表征算法稳定性。
(2)平均相对误差
为表征目标跟踪的滤波收敛情况,对跟踪成功的多次仿真结果进行统计分析,得到目标跟踪各时刻的平均相对误差
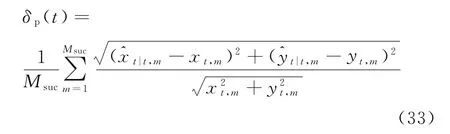
式中:(xt,m,yt,m)为第m次跟踪成功时目标在t时刻的位置信息,t=1,2,…,N;为第m次跟踪成功时目标在t时刻的位置估计值。
2.2 多种数据关联算法对比仿真
设目标的运动参数信息如表2所示,目标特征参数信息如表3所示。

表2 目标运动参数
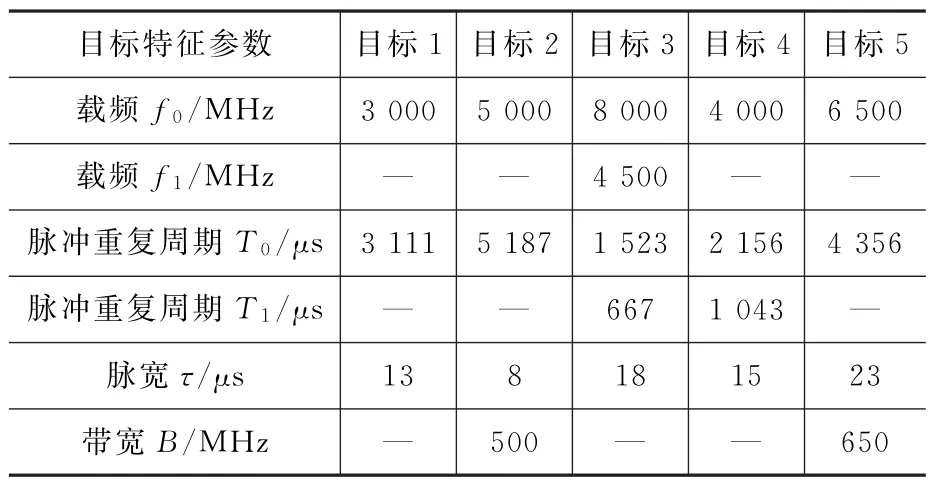
表3 目标特征参数
设杂波密度λ=0.01/km2,侦查站位于坐标系原点处,量测距离相对误差为1×10-3,角度误差为0.1°,频率测量误差为5 MHz,脉冲重复周期测量误差为10μs,脉宽测量误差为0.2μs,采样时间间隔T=0.5s,采样点数n=1~200,进行500次蒙特卡洛仿真实验。设定跟踪成功相对精度门限为1.5×10-3,统计采用5种数据关联算法成功跟踪目标的实验次数,其各自的量测分布、跟踪航迹及跟踪平均相对误差曲线如图2~图6所示。
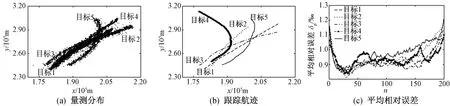
图2 PDA算法
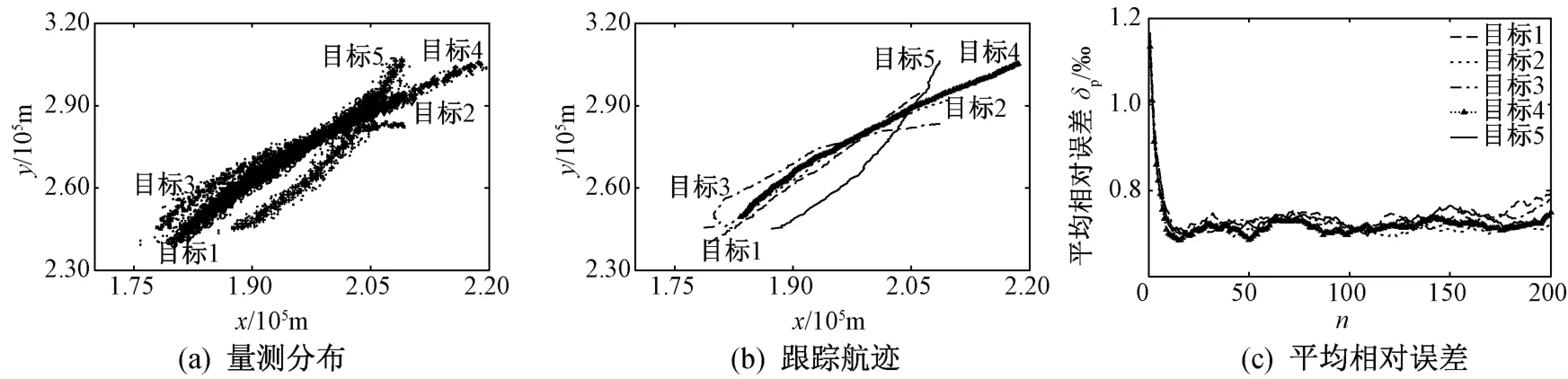
图3 JPDA算法
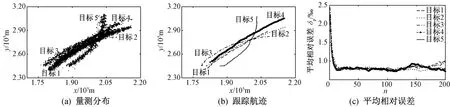
图4 GRDA算法
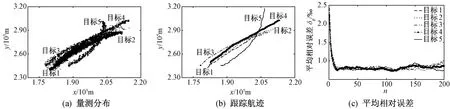
图5 GRED-DA算法
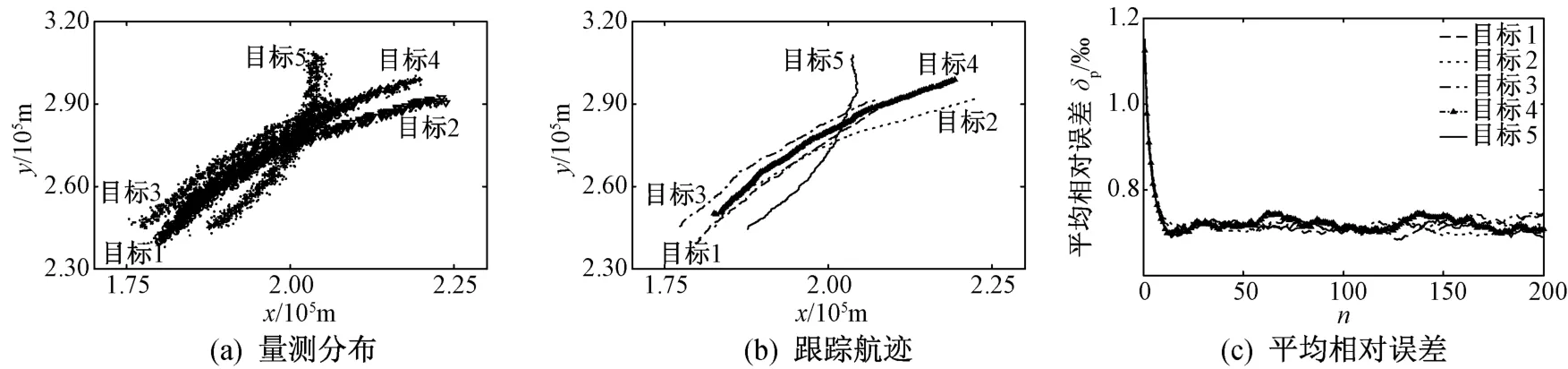
图6 HFS-DA算法
由图2~图6可知:采用PDA算法的非线性目标跟踪结果,大多误差较大甚至不收敛;采用JPDA、GRDA和GRED-DA三种数据关联算法成功实现多目标跟踪时,它们各自的平均相对误差变化曲线收敛状况之间差距并不明显;采用HFS-DA算法进行目标跟踪时,跟踪误差收敛性最好。
表4和表5分别给出了各关联算法在杂波环境下应用于目标跟踪时的跟踪成功率和程序运行时间。可知,相同条件下,PDA算法的运行时间最短,但跟踪成功率很低,无法满足工程应用需求。JPDA算法复杂度最高,运行时间也最长,跟踪成功率较高。GRDA算法与JPDA算法相比较,运行时间缩短了一半,这是由于该算法简化了量测与目标的概率匹配过程,但同时也使得跟踪成功率随之发生明显下降。GRED-DA算法利用证据距离法来计算各量测与目标的关联概率,在一定程度上提高了目标跟踪成功率,但也带来了极大的计算负担。HFS-DA算法利用特征对公共量测的匹配过程进行了辅助简化,且融合多种信号类型下的关联度求取公共量测的分配概率,将多目标跟踪转化为单目标跟踪问题,充分发挥PDA算法在单目标跟踪中的优越性,获得了更高的目标跟踪成功率,且算法处理速度更快。
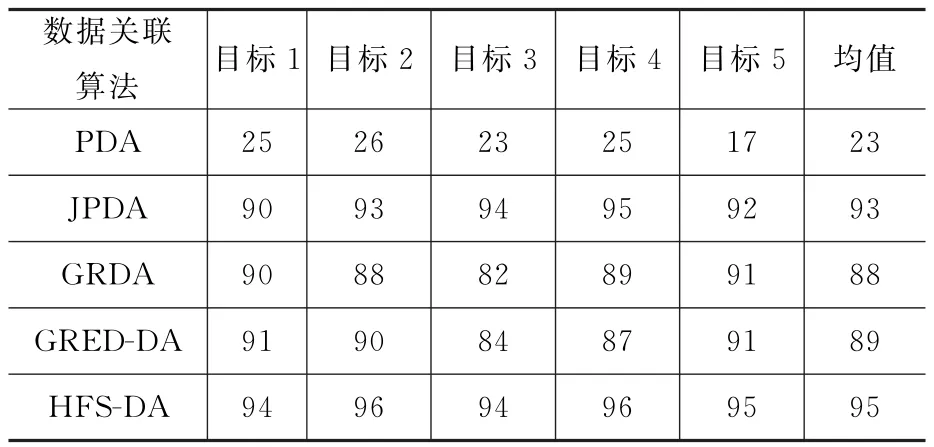
表4 各关联算法跟踪成功率 %
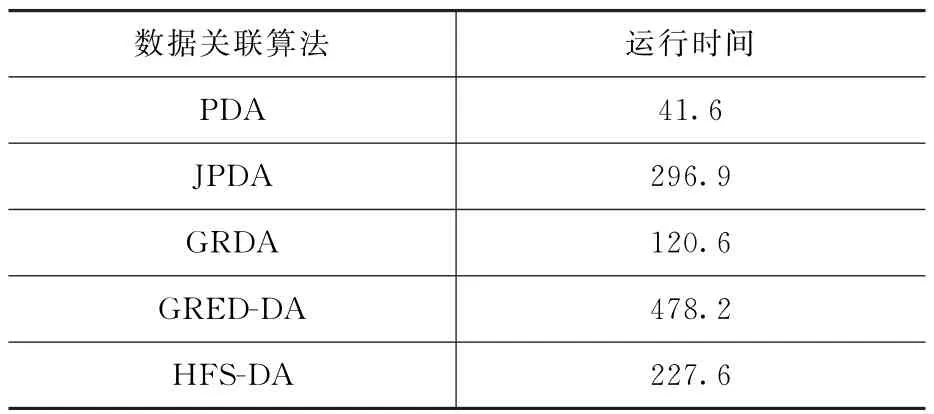
表5 各关联算法运行时间 s
2.3 不同环境条件下的对比仿真
分别采用JPDA、GRDA、GRED-DA和HFSDA算法对多个机动目标进行跟踪仿真实验。设定跟踪成功相对精度门限为2×10-3,改变量测误差和杂波密度,各算法的平均跟踪成功率及500次蒙特卡洛仿真实验运行时间如图7所示。
从图7(a)、图7(b)中不难看出,随着量测误差的增大,四种关联算法的关联准确性均会下降,再加上跟踪滤波算法本身的局限性,最终导致了目标跟踪成功率的下降。但采用HFS-DA算法得到的跟踪成功率一直高于另外三种算法,且算法实时性较高。而如图7(c)所示,随着杂波密度的增大,HFS-DA算法的关联准确率下降并不明显,特别是在杂波密度大于0.07/km2时,该算法的优越性愈发凸显出来,不仅关联准确性明显高于其他算法,算法实时性也最优。
综上所述,在非线性多目标跟踪过程中用HFS-DA算法进行数据关联,能在保证实时性的前提下,提高跟踪成功率,明显降低错跟、失跟现象发生的频率,增强目标跟踪系统的整体稳定性。
3 结论
在密集杂波和噪声环境下,由于各种不确定环境因素的影响,对近距离做小角度交叉非线性运动的多个目标进行跟踪时,可能发生跟踪收敛速度慢甚至发散的情况。为提高非线性多目标跟踪算法的稳定性,结合犹豫模糊集思想提出一种特征辅助数据关联新方法,简化了公共量测与各目标关联的概率匹配过程。同时将多种信号类型下的关联概率进行融合,避免由于信号类型识别错误而导致较大的关联跟踪误差,提高了数据关联稳定性。仿真对比结果表明:HFS-DA算法相较PDA、JPDA、GRDA和GRED-DA算法跟踪成功率分别提高了72.1%,2.6%,7%和6.5%;相对其中跟踪成功率较高的JPDA算法,HFS-DA算法的运行时间缩短了23.3%,算法实时性更强。由此证明HFS-DA算法可提高关联准确度,从而得到更高的跟踪精度,且实时性较强,更符合工程实践需求。
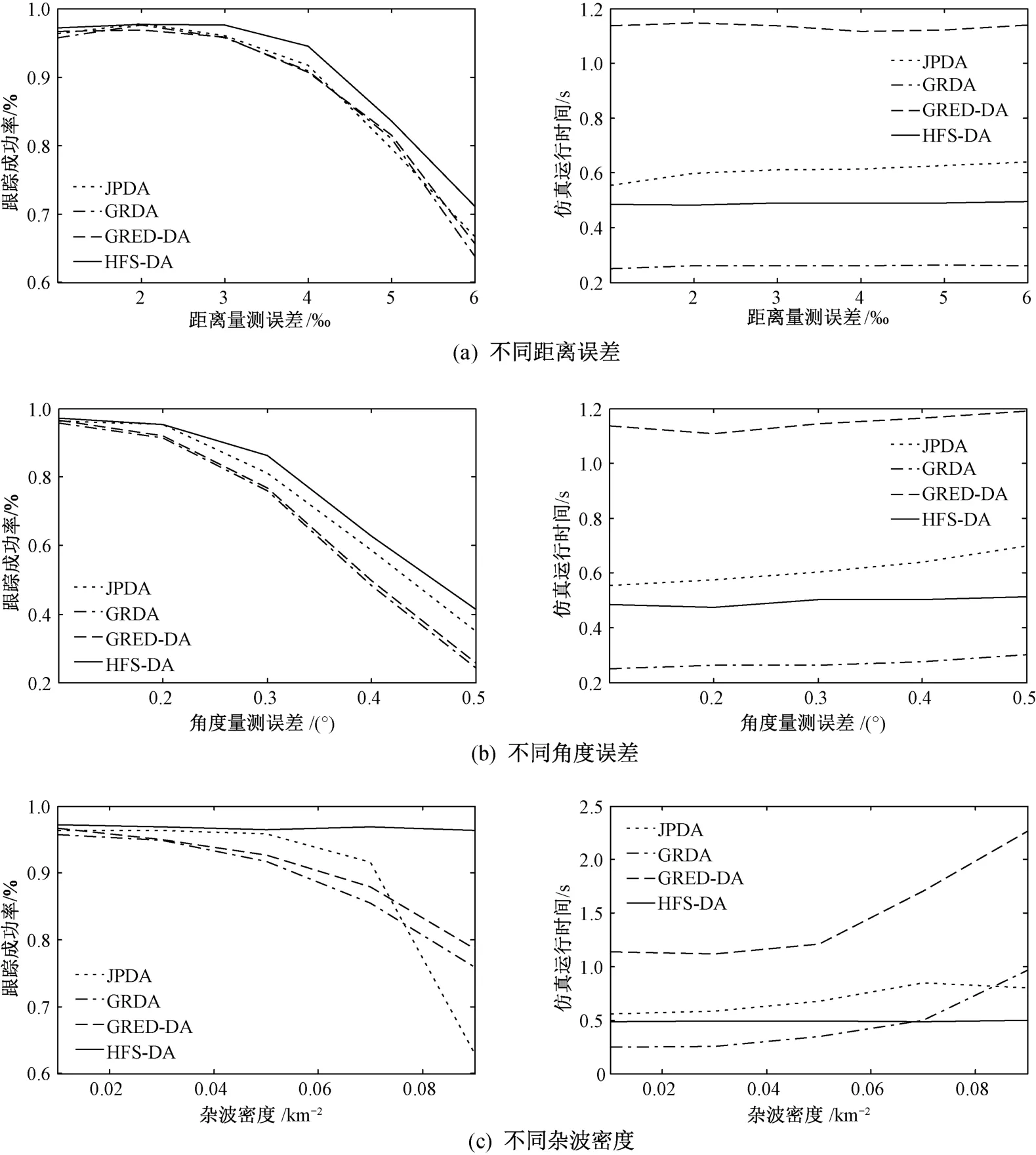
图7 不同仿真条件下的跟踪成功率及仿真时间对比
