一种太赫兹测云雷达高精度谱矩估计方法

张荣政, 肖 建, 沈艳秋, 王海涛, 赵 前

(上海无线电设备研究所,上海201109)

0 引言

云作为地球辐射收支系统的重要调节器,在大气能量循环、水循环以及地气系统中扮演着非常重要的角色。太赫兹雷达相比于毫米波雷达对非降水云的观测具有更高的灵敏度,可用于获取云内部信息。太赫兹主动云探测技术既能有效弥补当前云遥感手段中冰云探测能力的不足,又有助于提升云相关参量数据反演的精度,对促进天气预报和气候预测的研究具有重要意义[1]。

为准确反演云参数,需要精确提取云回波的谱矩信息,即完成对气象粒子的雷达反射率因子、平均多普勒速度和速度谱宽的估计。目前,国内外新一代脉冲多普勒全相参体制的天气雷达,常用的谱矩估计方法有基于功率谱密度函数的估计法[2](简称传统谱处理法)以及基于自相关函数的脉冲对处理(Pulse Pair Processing,PPP)法[3-4](简称脉冲对处理法),其中传统谱处理法较为灵活且应用范围较广。由于气象回波信噪比通常很低,需要通过信号积累以及噪声抑制等手段才能获得较好的谱矩估计结果。

当前传统谱处理法在高信噪比条件下的应用效果良好,但是该方法在回波信噪比低且相位噪声差的太赫兹测云雷达系统中表现稍差,速度和速度谱宽估计精度不高。脉冲对处理法对稳定干扰的抑制效果较差,在早期天气雷达中应用较为广泛,本文不再进一步讨论。本文利用信号频域处理的灵活性以及自相关处理对随机信号良好的抑制特性,提出了一种基于频域处理的自相关谱矩估计法来提取速度和速度谱宽参数。并通过实验仿真,验证该方法在太赫兹测云雷达系统中应用的有效性。

1 谱参数估计方法

基于频域处理的太赫兹测云雷达自相关谱矩估计法主要包括回波信号相干积累、频谱处理(如加窗、取模平方等)、谱平均以及速度和速度谱宽估计等步骤,最终获得云回波的速度和速度谱宽参数。

1.1 相干积累

相干积累主要用于提升气象雷达的回波信噪比。气象雷达接收的回波信号中,气象目标回波信号常常淹没在噪声中,单个回波脉冲的信噪比很低。为了提高信噪比,有效提取气象信息,需要对回波信号进行相干积累。基于回波信号相干的特性,将多个相邻脉冲的回波信号进行平均和去直流操作,该过程实质是时域平均滤波,且操作简单。假设太赫兹测云雷达接收到的回波信号x(n)包括气象目标回波信号s(n)和干扰c(n),可以表示为

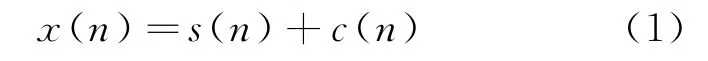
设x(n)的脉冲重复频率为fp,将回波信号x(n)积累M次得到的信号可表示为

雷达回波中的噪声和气象目标回波信号相互独立,相干积累后的信号可以认为是气象目标信号和噪声的各自平均之和,则

M次相干积累理论上可使回波信噪比提高M倍。实际应用中,由于回波信号相干时间的限制以及速度测量范围的要求,相干积累的次数通常受限。因此,时域相干积累的次数需要根据实际情况确定。

1.2 频谱处理

观测和理论研究表明,大部分气象回波信号在同一距离门内的功率谱服从高斯分布[5]。考虑到在频域内处理稳定的杂波和直流信号具有较大的优势,且当前硬件水平完全满足傅里叶变换的运算要求,故对相干积累后的回波信号进行加窗、取模平方、杂波抑制和去直流等处理。得到某一距离门内回波信号的功率谱密度函数S(fi),可表示为

式中:fi为信号频率;N为总采样点数;w(n)表示窗函数。S(fi)具有能量密度的意义,反映了信号能量的分布情况。

1.3 谱平均

由于气象目标存在较强的起伏现象,气象雷达接收到的信号经过相干积累和单次频域处理后得到的功率谱具有较强的脉动性。为了减小其脉动,一般采用谱平均的方法来使功率谱变得平稳。所谓谱平均就是将多次谱分析得到的功率谱叠加后求平均值。将功率谱密度S(fi)进行K次平均,平均功率谱可表示为

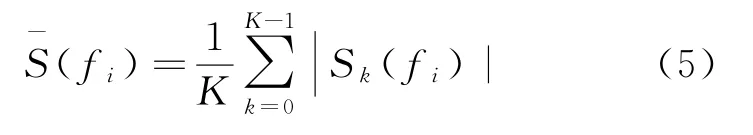
除了减小功率谱的脉动外,谱平均也能够提高回波信噪比。谱平均处理过程实际是对回波非相参积累处理的过程,进行K次功率谱平均后,回波信噪比理论上可以提升倍。直观上来看,只要进行足够次数的谱平均,就可以获得较高的信噪比。但在实际应用中,谱平均次数受到各种条件的限制,其中最主要的限制包括两个方面:一是进行谱平均的前提是气象回波信号多普勒谱的特征保持不变,但实际情况下气象目标特征的保持时间是有限的,因此谱平均的次数不能是无限的;二是雷达输出的数据要保持一定的时间分辨率,所以谱平均的时间或次数也会限定在一定范围内。

1.4 速度和速度谱宽估计

气象回波信号经过前面步骤处理,可获得相对稳定的多普勒功率谱密度函数。考虑到气象回波信号是广义平稳的确定性信号,符合维纳-辛钦定理,因此,对式(5)获得的平均功率谱进行逆傅里叶变换处理,即可获得不同时间延迟的自相关函数值。基于自相关函数可估计出云目标的平均速度及速度谱宽,表达式为

式中:Ts表示发射信号的脉冲重复周期;arg(·)是相位求取函数分别表示回波信号的0阶自相关及延迟Ts后的自相关;L表示总采样点数;l表示脉冲序列间延迟,其中l取0和1时,分别对应。

总之,从回波功率谱函数很容易获得自相关函数值,且计算量较小。本文提出的方法与传统谱处理法在运算量上相当。另外,由于谱域平均对杂波和噪声脉动抑制以及自相关处理对随机信号的抑制作用,使得该方法相比于传统谱处理法所估计的速度和速度谱宽参数精度更高。

2 算法仿真

观测和理论研究表明,大部分气象回波的功率谱近似服从高斯分布,回波数据模拟分析功率谱可采用高斯分布表征。利用MATLAB软件对本文提出的基于频域处理的自相关谱矩估计法进行仿真,同时与天气雷达广泛应用的传统谱处理法的仿真结果进行对比。

太赫兹测云雷达采用线性调频脉冲压缩体制,工作频率为220GHz。具体的仿真参数:波长1.4mm,带宽12MHz,脉冲重复周期200μs,脉冲宽度2μs,傅里叶变换点数64,谱平均次数8,平均速度0.5m/s,速度谱宽0.2m/s。在信噪比为10dB的情况下,仿真的云回波经过本文方法处理后的功率谱如图1所示。

图1 模拟云回波多普勒功率谱

因气象回波信号有脉间起伏并存在噪声,利用本文方法得到的功率谱形状略有参差,但是基本满足高斯分布的谱型,且均值和方差也与理想分布一致,增加谱平均次数可令谱线更接近高斯分布。两种谱矩估计方法计算结果如表1所示。可见,估计结果与仿真输入参数基本一致。

表1 信噪比10dB时的谱估计结果

为验证本文方法的可靠性,设置多普勒速度为0.5 m/s,速度谱宽为0.2 m/s,信噪比在(-15～+20)dB之间变化,信噪比变化步进为5dB,对应于每个信噪比均做100次蒙特卡罗仿真实验。图2为两种方法的平均速度和速度谱宽估计蒙特卡罗实验结果。

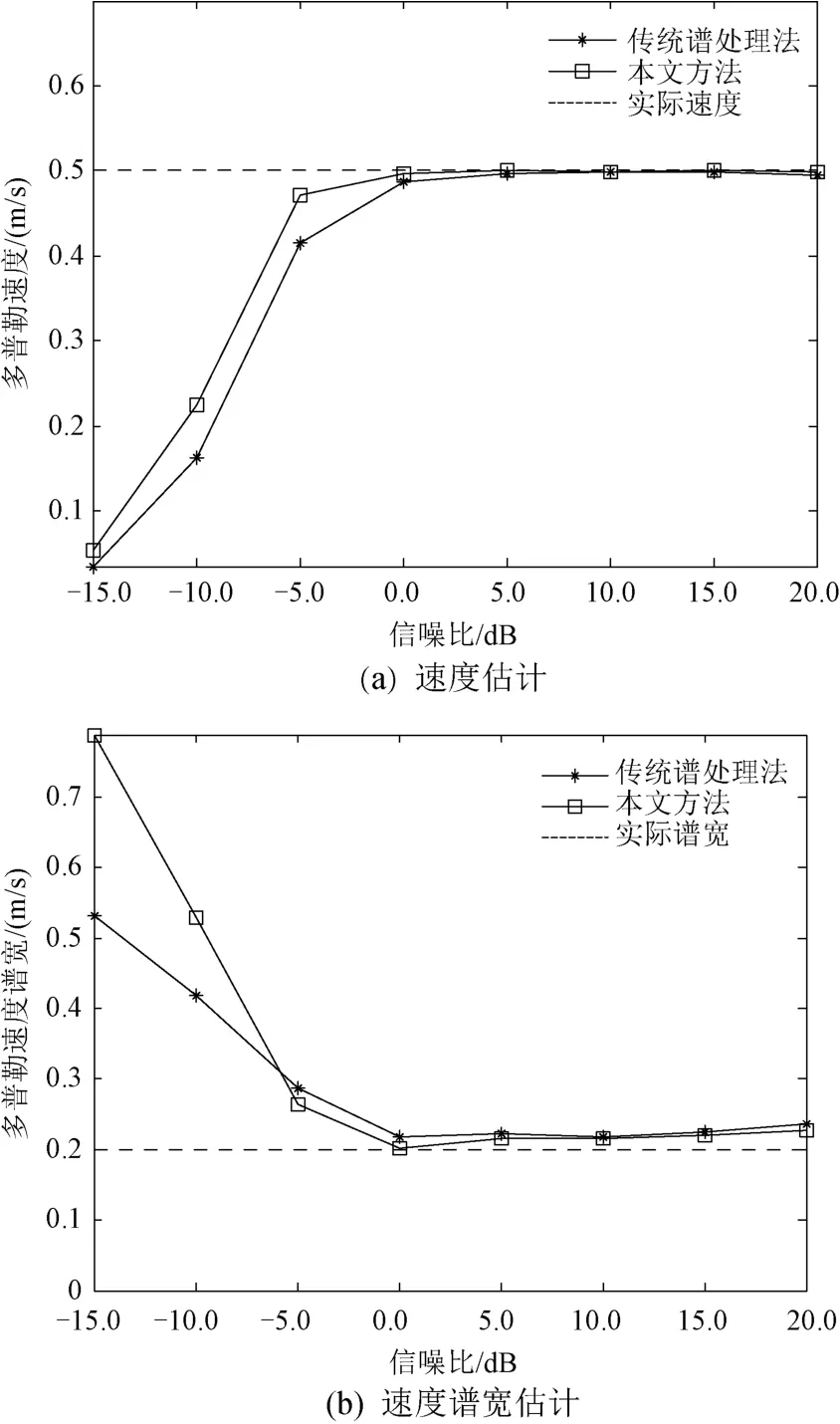
图2 平均速度和速度谱宽的蒙特卡罗仿真结果

从图2(a)可以看出:在信噪比大于5dB的高信噪比的条件下,传统谱处理法和本文所提的方法均能精确估计平均速度;当信噪比为(-5～+5)dB时,本文所提的方法平均速度估计结果精度仍较高,而传统谱处理法估计得到的平均速度随信噪比的降低,与真实值的偏差逐渐增大;信噪比小于-5dB时,两种方法估计性能均恶化严重。由图2(b)可以看出:两种方法的速度谱宽估计结果都略微大于真实值,但是误差在信噪比大于5dB时都能保持稳定,满足估计的要求;随着信噪比下降,当信噪比小于-5dB时,估计值逐渐偏离真实值。

根据图2的仿真结果,可以发现无论是平均速度估计还是速度谱宽估计,利用本文所提的方法性能均优于传统谱处理法,且两种方法的运算量相当。因此,在设计太赫兹测云雷达系统时,可优先选取本文所提的方法。

3 结论

针对现有云目标速度和谱宽参数估计方法对噪声抑制效果差,而造成估计精度降低问题,本文在频域处理的基础上,结合自相关谱矩估计,提出了基于频域处理的自相关谱矩估计法。利用MATLAB软件仿真了整个处理流程,并选取传统谱处理法作为比较对象,以验证本文所提的方法的有效性。结果表明,基于频域处理的自相关谱矩估计法的速度和速度谱宽估计精度均优于传统谱处理法,可用于太赫兹测云雷达中。