信道化结构的无乘法器优化与实现

崔鑫磊, 陆满君, 张文旭, 何俊希

(1.哈尔滨工程大学信息与通信工程学院,黑龙江 哈尔滨150001;2.上海无线电设备研究所,上海201109;3.南京航空航天大学电磁频谱空间认知动态系统工信部重点实验室,江苏 南京211106;4.哈尔滨工程大学工业和信息化部先进船舶通信与信息技术重点实验室,黑龙江哈尔滨150001)

0 引言

电子战作为现代信息化战争中的重要一环,发挥着越来越来重要的作用。在现代化战场中,传输的信号具有密度大、形式复杂的特点。面对日益复杂的电磁环境,宽带接收机面临着越来越严峻的考验。在实际应用中,判定接收机性能优劣的重要标准是其能否做到对信号进行全概率截获。如果一个接收机能处理大瞬时带宽信号,拥有大的动态范围与高灵敏度,同时能实时接收信号,则能够在复杂的电磁条件下进行信号的有效截获[1]。信道化接收机能分辨时域重叠信号,具有较高的灵敏度和频率分辨率,截获概率接近100%,是目前唯一实用且满足电子战需求的宽带接收机。

信道化接收机技术在近些年迅速发展,信道化理论日趋成熟。其中基于离散傅里叶变换(Discrete Fourier Transform,DFT)的多相滤波信道化结构是一种基本的信道化结构,在研究过程中多相结构被不断进行改进[2]。频率响应屏蔽(Frequency Response Masking,FRM)技术[3]被用于原型低通滤波器的设计,以获得较窄的过渡带宽和较低的资源占用。同时涌现出多种基于多相滤波结构的信道化接收机优化方法[4]。

在对整数进行二进制量化编码[5]时,一般会使用二进制补码(Two's Complement,2C),或通过正则有符号数(Canonic Signed Digit,CSD)编码对整数进行转换,减少非零元素,提高硬件实施效率[6]。正则表达式与普通二进制转换的最大区别是具有三重值,其取值值域为{0,1,-1}。在算法硬件实现中运用CSD编码方法,有利于提高运算速度和减少资源的占用。

动态旋转因子(Dynamic Twiddle Factor,DTF)算法是减少DFT在硬件上资源消耗的一种方法[7],它是传统定点旋转因子算法的延伸。在动态旋转因子算法中,旋转因子会被量化成与原旋转因子误差最小、分子分母都为整数的分数形式。

信道化接收机在硬件实现过程中会消耗大量的乘法器资源,将CSD编码技术和改进动态旋转因子算法应用到基于FRM的多相信道化接收机中,可以将乘法器资源的占用转化为移位器与加法器的占用,提高硬件实现的效率,降低延迟。

1 基于FRM的多相信道化结构

基于FRM的多相数字信道化结构结合了FRM技术与多相结构[8]的优点,既可以达到更低的计算复杂度,也可以实现窄过渡带的设计目标。信道化滤波器可以通过对原型低通滤波器进行调制实现,所以首先需要设计窄过渡带的原型低通滤波器。将FRM技术[9]应用到原型低通滤波器的设计中,可以得到低复杂度的窄过渡带低通滤波器,其传递函数为

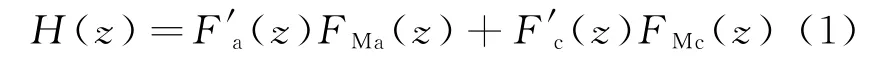
式中:F'a(z)和F'c(z)是低通滤波器Fa(z)和它的互补滤波器Fc(z)进行L倍插值后得到滤波器;FM]a(z)和FM]c(z)分别是长度为NM]a和NM]c的屏蔽滤波器。

FRM的具体实现方法如图1所示。首先选择一个过渡带相对较宽的低通滤波器Fa(z),通过运算得到它的互补滤波器Fc(z);然后进行L倍插值得到F'a(z)和F'c(z);最后选择合适的屏蔽滤波器FM]a(z)和FM]c(z),运算得到窄过渡带低通滤波器H(z)。

Fa(z)和Fc(z)满足

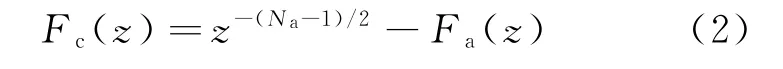
式中:Na为Fa(z)和Fc(z)的长度。

对Fc(z)进行L倍插值,由式(2)可得

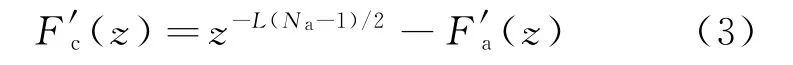
将式(3)代入式(1),可得

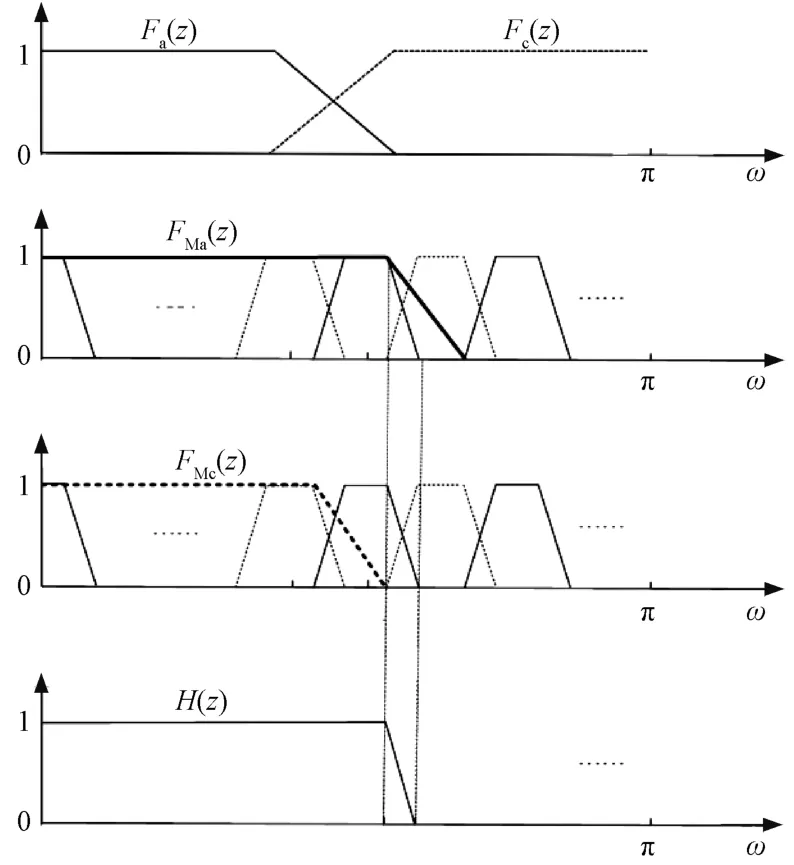
图1 基于FRM的低通滤波器实现过程

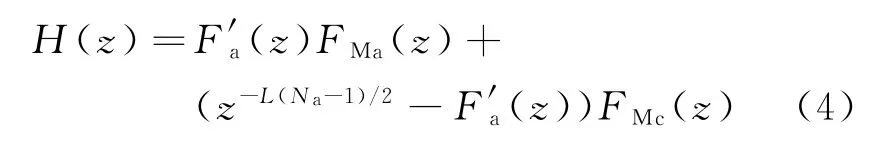
各子信道滤波器Hk(z)可由窄过渡带低通滤波器H(z)经过复指数调制得到,表达式为

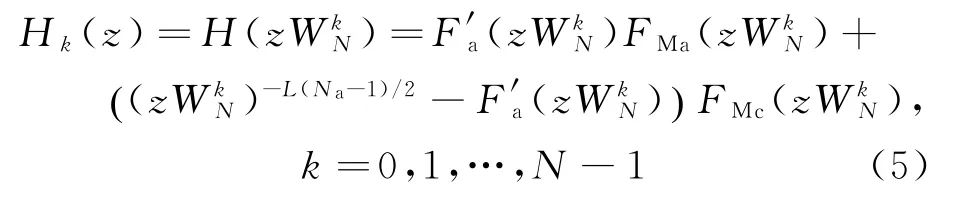
式中:N为数字信道化结构中信道的个数;调制因子

对滤波器Fa(z)进行L倍插值后会产生L个附加镜像,而且相邻信道的中心频率间隔为2π/L。若使插值因子L为信道数N的整数倍,在利用调制因子对插值后的滤波器Fa(z)进行复指数调制时,原型低通滤波器并不会发生改变,即

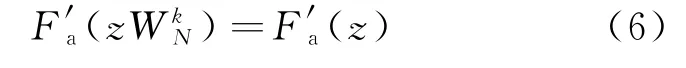
将式(6)带入式(5),Hk(z)进一步化简为

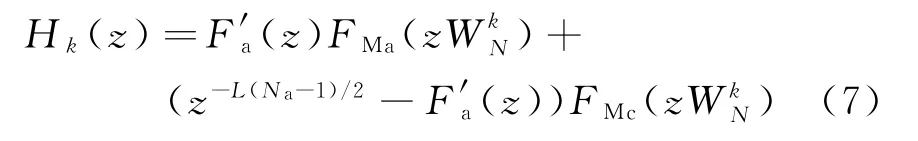
对屏蔽滤波器FM]a(z)和FM]c(z)进行多相表示,可得

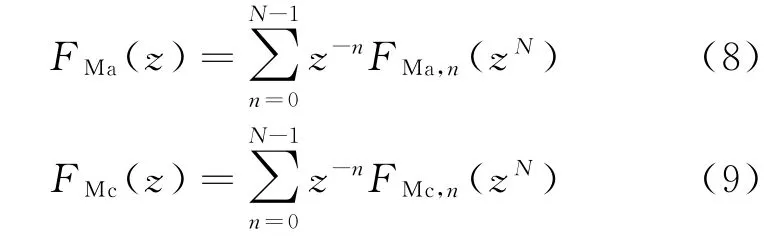
由式(8)和式(9)可得

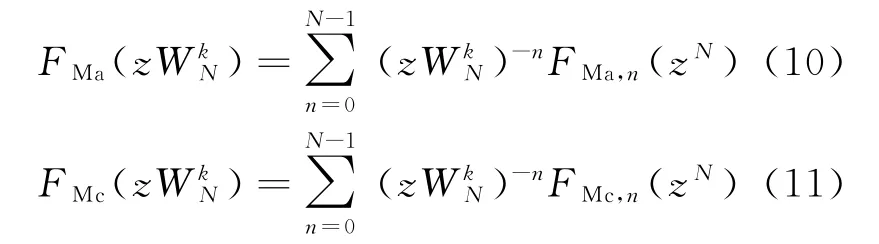
将式(10)和式(11)代入式(7),可得

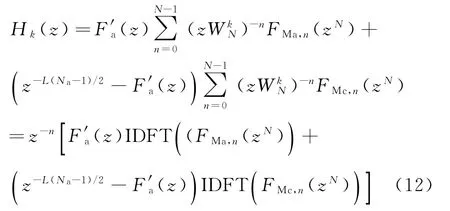
式中:IDFT(·)表示对括号内信号进行离散傅里叶逆变换。

将抽取模块置于滤波器组结构之前[10],根据式(12)可以得到基于FRM的多相数字信道化结构,如图2所示。x(n)和yk(n)分别为输入、输出信号。

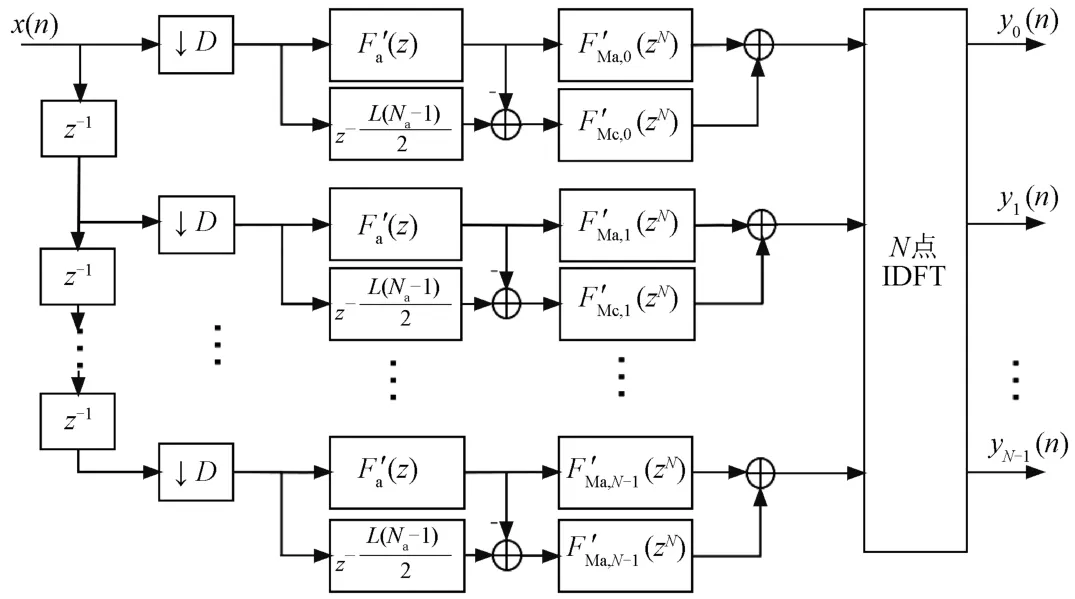
图2 基于FRM的数字信道化结构

2 数字信道化结构优化设计

2.1 无乘法器FRM滤波器组设计

在工程实现中,可以通过CSD编码对整数进行转换,以减少非零元素,来提高硬件实施效率。CSD编码原则是从低位到高位,遇到连续的两个1,就将其改写成0和-1。高位1变0,低位1变-1,不看-1的符号位的话,相比原来少了一个1,这个少了的1要进位到高位,以此类推。例如,011改写为10(-1)。

乘法是数字滤波器中的主要运算之一。对于硬件设计来说,在进行常系数滤波器的优化设计时,一般可以利用移位器与加法器结合,来取代常规的数据与常系数的乘法运算。该方法能避免硬件实现上高乘法器资源占用和高延时的问题。设FIR滤波器的数学表达式为

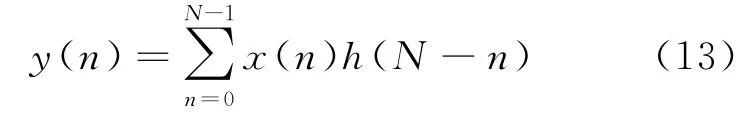
式中:x(n)为输入信号;h(n)为滤波器单位冲激响应;N为滤波器长度。

令xi=x(i),yi=y(i),hi=h(N-i),基于CSD编码,可以将式(13)变换为

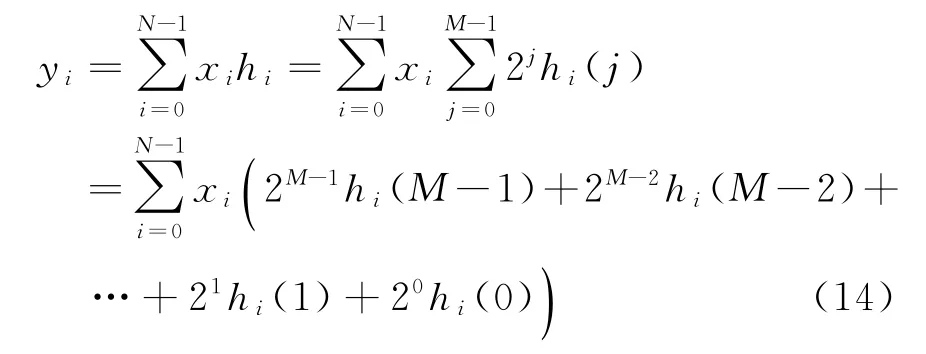
式中:M代表滤波器系数量化位数;hi(j)为hi的CSD编码的第j位,取值为0,-1或1。每一个1值代表一次加法运算,-1代表减法运算,0值不需要运算。

CSD编码可以降低滤波器非零元素数量,即降低滤波器运算需要的乘法器数量,相应占用的寄存器与查找表数量也会降低。假设X为输入,Y为输出,H为系数。当H=(31)1]0时,有

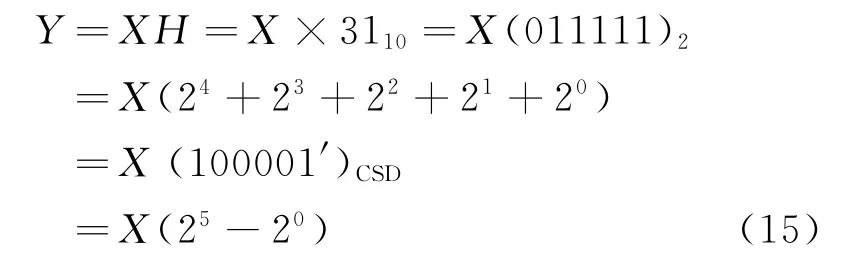
式中:1'表示-1。

普通二进制编码系数与输入信号相乘的移位相加实现结构如图3所示。CSD编码系数与输入信号相乘的移位相加实现结构如图4所示。

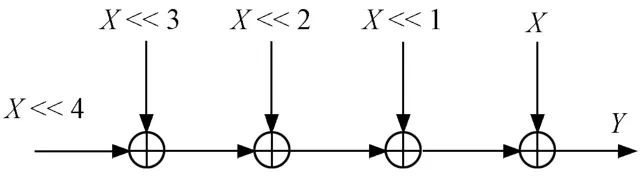
图3 优化前乘积组合

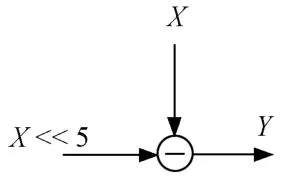
图4 优化后乘积组合

由上文可知,滤波器中系数与输入信号的乘法运算,可转化为输入信号自身的移位与加法运算。如图3和图4所示,当滤波器系数第n位的绝对值是1时,输入信号左移n位,最后将所有移位结构相加减得到乘法运算结果。在硬件实现中可以将乘法器占用转换成移位器与加法器的占用,这种方法能够减少硬件计算时间。

2.2 基于改进动态旋转因子算法的无乘法器定点IFFT设计

对于一般的时域信号,可以利用DFT将其转换成离散频域信号,表达式为

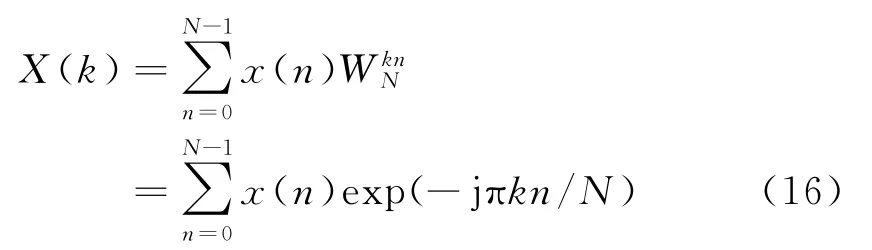
式中:x(n)为模拟信号的采样输出;X(k)为离散傅里叶变换后的第k个数据;N为数据个数。

快速傅里叶变换(Fast Fourier Transform,FFT)同样可以应用于IDFT计算,称为快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)。其中IDFT公式为

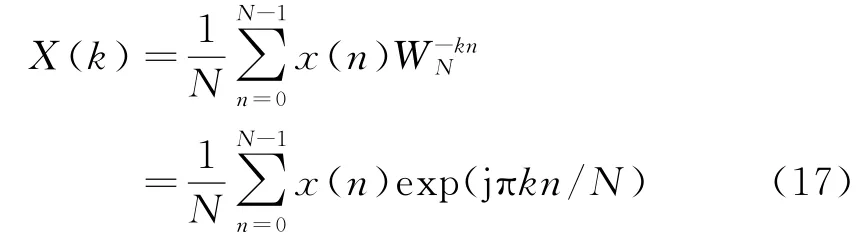
IDFT运算与DFT间的区别在于IDFT中需要把原DFT公式中的系数换为,并乘以常数1/N。根据得到的IDFT计算公式,IDFT算法的理论与硬件结构也得以确定。

在N点IDFT中,存在N个旋转因子与数据的乘法运算。通常旋转因子为复数,实部和虚部的值小于1,这会极大提升硬件实现的复杂度,同时消耗大量的硬件资源。

在动态旋转因子算法中,旋转因子会被量化成与原旋转因子误差最小、分子分母都为整数的分数形式。为了进一步降低数据与旋转因子的处理复杂度,可将分子分母量化为2的幂次方。例如,对于8bit输入数据的情况,旋转因子的实部和虚部可量化为(96/128,84/128)。其中,数据与实部相乘转化为数据分别向右移一位和两位的加和,数据与虚部的相乘运算与实部相同。这样可使量化后的整数与数据的乘法运算,转化为数据自身的移位与加法运算。

当决定旋转因子的量化表达形式时,传统方法会尽可能选取与原旋转因子的误差最小的取值点。对于DFT计算而言,这不一定是计算量最小的选择。对于大型的DFT计算,不选择计算量最小的取值点会在硬件上多消耗大量的加法器。为了在保证精度的前提下进一步降低量化过程带来的资源消耗,应使用加法次数最少的量化值取代原来的量化结果,同时大比特数的量化能使量化误差控制在一定范围之内。以256点FFT中的一个旋转因子为例,其复数表达式为

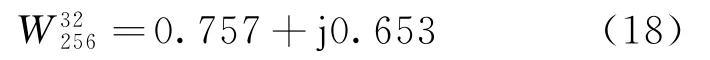
将复数的实部和虚部量化为分母为128的分数时,可以得到4种量化值:(97/128,83/128),(96/128,83/128),(97/128,84/128)和(96/128,84/128),如图5所示。

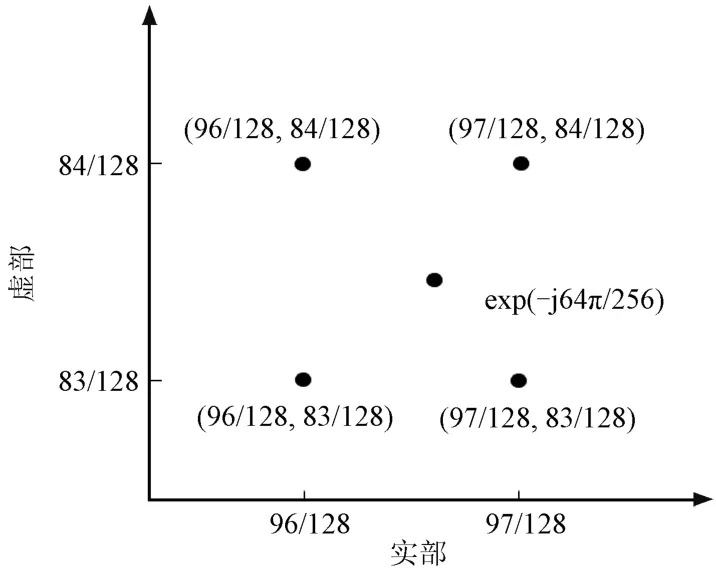
图5 传统旋转因子算法取值与改进DTF算法取值

在图5所示的4种量化选择中,(97/128,83/128)为传统DTF方法量化的结果,其余为临近的量化坐标点。其中实部量化值97/128可以分解为1/2,1/4,1/128的和;96/128可以分解为1/2与1/4的和。可以看出,当选择96/128作为量化选择的时候,能够在保证一定精度的前提下,节省更多加法器。虚部的量化选择方法与实部相同,当所有的旋转因子经过优化和重新选择后,整个IDFT流程的硬件资源占用情况能得到进一步优化。

在传统FFT运算中,数据经过一级运算后会增加1bit以防止数据溢出。对于多点数FFT运算过程,过度增长的数据比特位不利于硬件实现。所以需要利用截位的方法来对数据进行截取。一般的截位方法是直接截取N位数据的高N-1位,用于下一级运算。这种方法对于强信号处理比较有效,对于低幅度的弱信号,其有效数据可能在中途被截除,造成FFT运算结果的失真。在改进的DTF算法中引入动态截位方法,可以有效处理弱信号。动态截位方法在FFT的每一级运算之后设置比较器,用于判断每一级输出的Nbit数据是否大于2N-1(Nbit数据可容纳的最大值)并输出一个标志位。如果输出的数据大于2N-1,则后续单元根据标志位截取数据的高N-1位;如果数据等于或小于2N-1,则截取数据的低N-1位。传统截位方法与动态截位方法的算法流程如图6所示。动态截位方法可以在不增加复杂的额外设计的情况下,更好地对弱输入信号进行处理。

图6 截位法流程图

3 数字信道化结构优化设计与仿真分析

3.1 基于无乘法器的数字信道化结构仿真

利用MATLAB对基于无乘法器的FRM数字信道化结构的正确性进行验证。FRM滤波器参数如表1所示。设采样率为1.92GHz,数字信道化结构的子频带个数N=16,抽取倍数L=32。

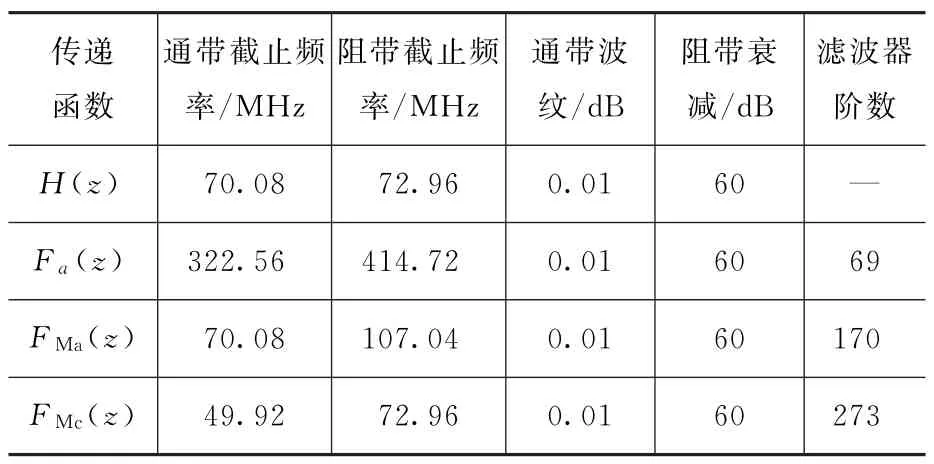
表1 FRM各滤波器参数

图7～图10分别为低通滤波器Fa(z),屏蔽滤波器FM]a(z)和FM]c(z),以及经频率响应屏蔽方法合成的窄过渡带低通滤波器H(z)的幅频特性曲线。

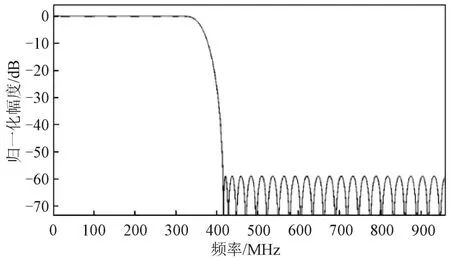
图7 低通滤波器Fa(z)幅频特性曲线

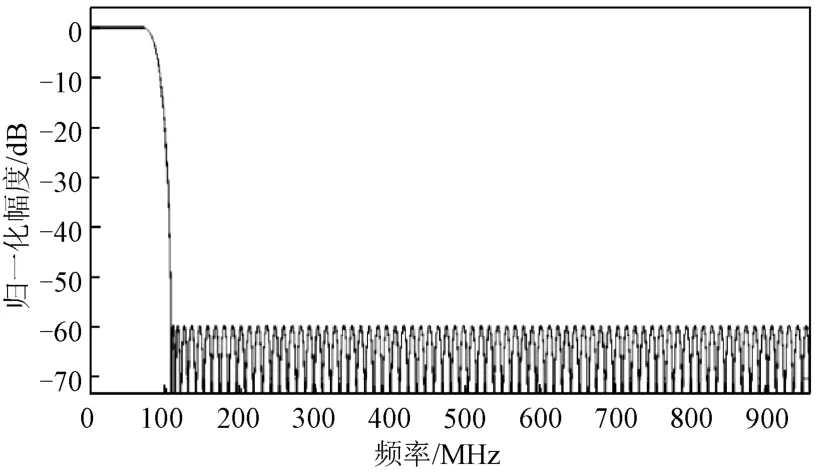
图8 屏蔽滤波器FM]a(z)幅频特性曲线

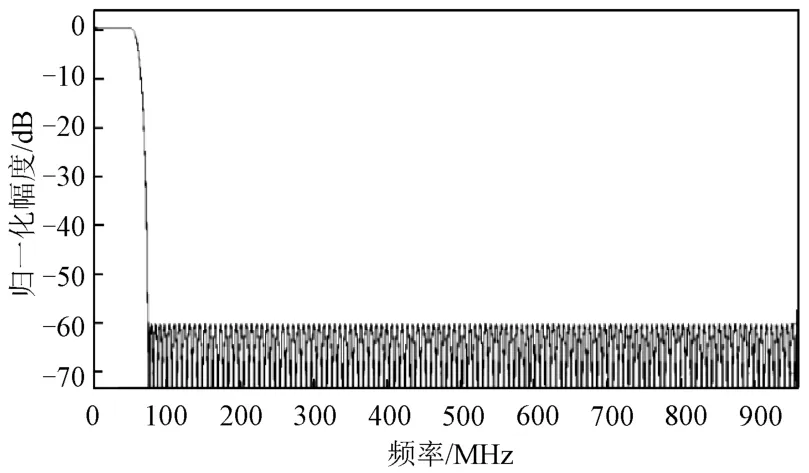
图9 屏蔽滤波器FM]c(z)幅频特性曲线

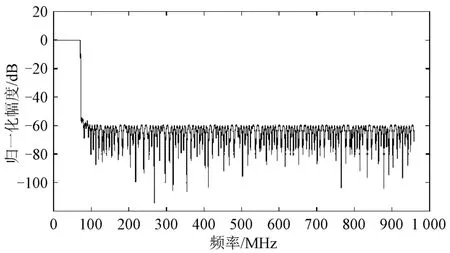
图10 窄过渡带低通滤波器H(z)幅频特性曲线

仿真输入为两个正弦信号,参数如表2所示。

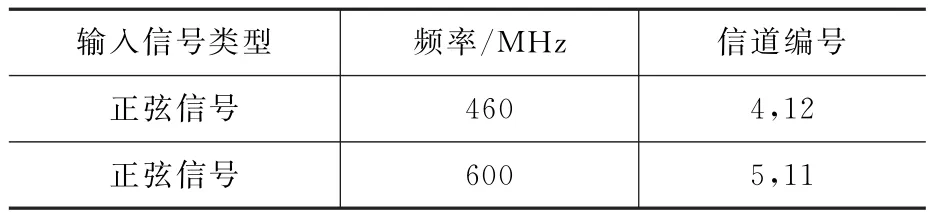
表2 输入信号参数

图11为16个子信道输出的信号频谱图。可以看出,频率为460MHz的正弦信号从信道4和12输出,而另一个正弦信号从信道5和11输出。其中每个信道的频谱峰值对应的横坐标轴数值表示信号与对应信道中频混频后的频率值。从子信道的频谱图可以看出,仿真结果和理论推导的信道输出情况相符,证明无乘法器优化的数字信道化结构的理论推导是正确的。

3.2 基于改进动态旋转因子算法的无乘法器定点FFT仿真

由2.2节可知,由于FFT运算与IFFT的主要区别在于系数不同,而且在单独验证时,FFT结构只需要输入预定好的采样信号,观察信号频谱即可,相较于IFFT,验证更方便。故在本节将基于改进动态旋转因子算法的无乘法器设计应用于FFT结构进行MATLAB仿真验证,间接证明优化设计对IFFT的有效性。

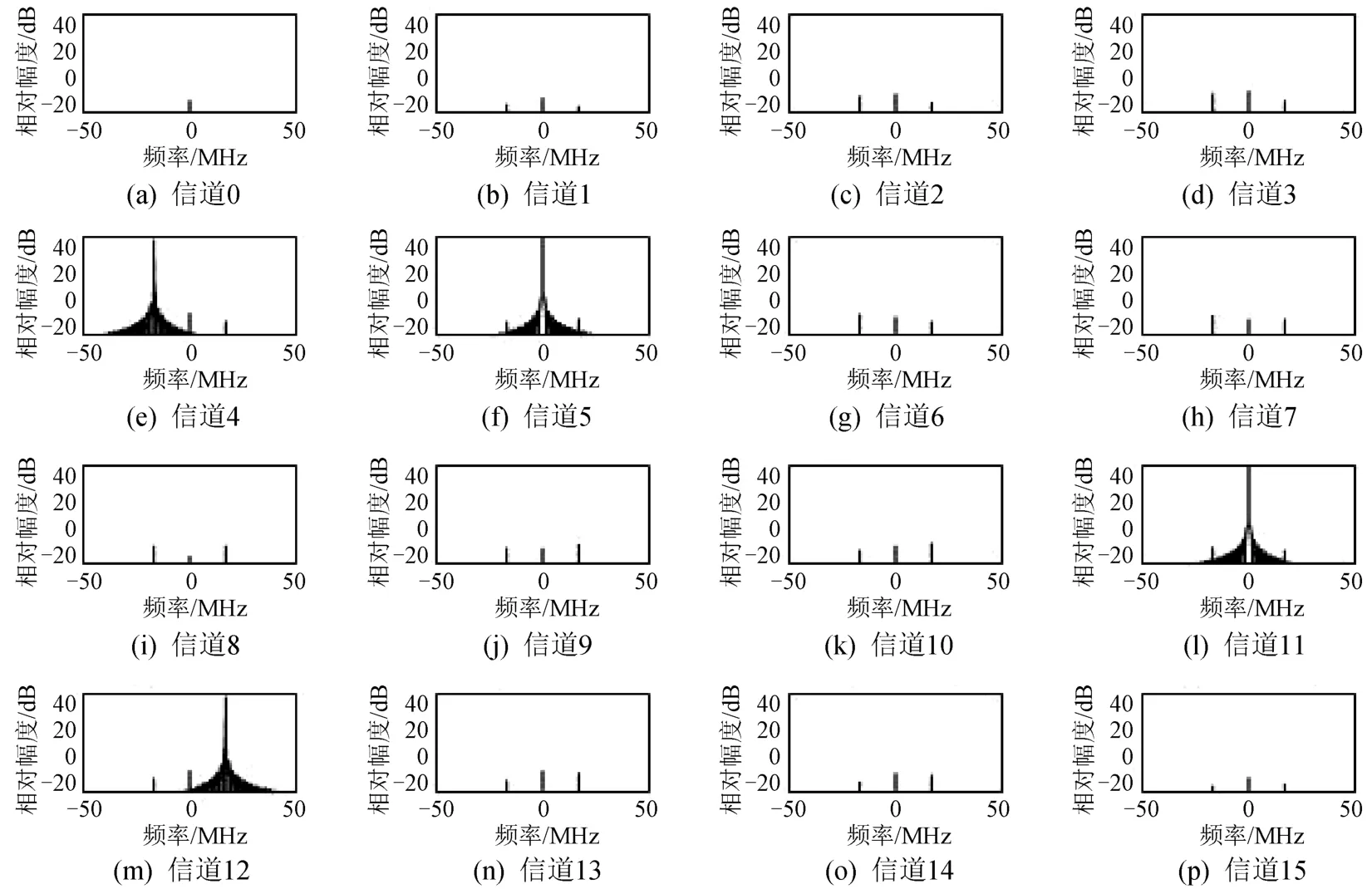
图11 输出信号幅频特性图

根据改进的DTF算法结构,首先在MATLAB软件上对2048点FFT进行仿真。其中仿真信号选用频率分别为15,40,50 Hz的正弦信号。设信号采样率为256Hz,使用传统截位方法及动态截位方法的输入输出信号频谱如图12所示,其中50Hz处频谱如图13所示。从图中可见,频率峰值处使用截位的DTF算法与传统FFT方法相比会有损失。其中传统截位方法的DTF算法会截除FFT每一级计算结果的末位数据,这种方法检测到的频谱幅度损失最高,会削弱对弱信号的检测能力;动态截位法的DTF算法的频谱图也存在损失,但与传统截位方法相比频谱损失更少。动态截位法的DTF算法与传统截位法的DTF算法相比拥有更优的计算性能。

3.3 硬件仿真及资源分析

为了对算法占用硬件资源情况进行对比分析,对基于无乘法器优化的数字信道化结构和传统的多相信道化结构进行FPGA硬件仿真。利用系统生成器(System Generator)软件对算法模块进行搭建,FRM滤波器参数如3.1节表1所示,仿真输入信号参数见3.1节表2,采样率为1.92GHz,选用16信道结构进行仿真。

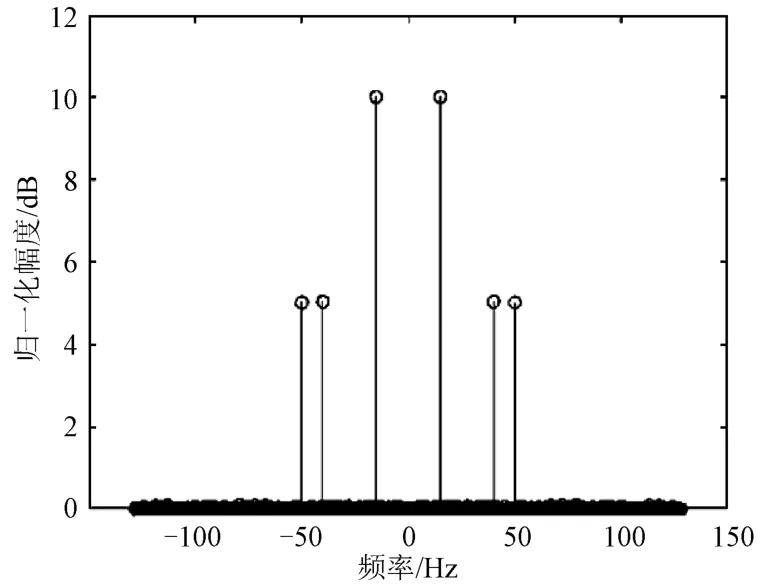
图12 信号频谱图

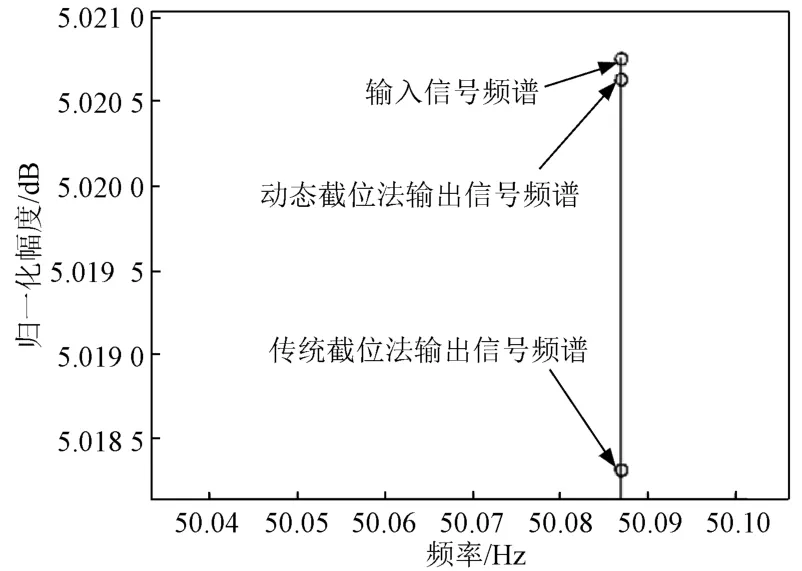
图13 50Hz处频谱放大图

选用Xilinx公司的Virtex6系列FPGA芯片XC6VTX550T进行硬件设计,时钟设置为3.7 ns,系统仿真频率为1.92 GHz。硬件设计实现完成后得到整个系统的硬件资源占用情况如表3所示。

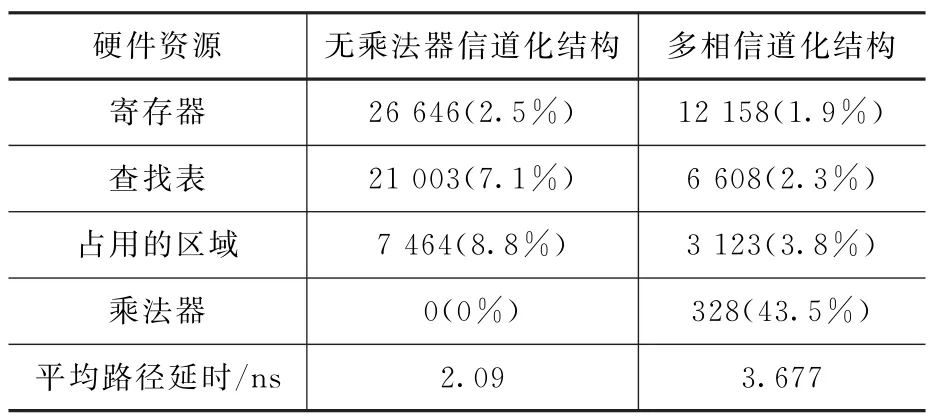
表3 硬件资源占用情况比较

对比表3中的资源占用率可以看出,在设计参数相同的情况下,无乘法器数字信道化结构相比于传统多相数字信道化结构,不占用乘法器资源,但寄存器、查找表和区域资源占用较多。这是因为无乘法器数字信道化结构在每条信道支路中相比于多相信道化结构多了两个滤波器,并且将乘法器转化为移位器与加法器会占用额外的查找表与寄存器资源。无乘法器数字信道化结构的平均路径延时为2.090ns,相比于多相数字信道化结构的3.677ns,延迟更低。总体而言,无乘法器数字信道化结构在有限损失寄存器、查找表和区域等资源的情况下,将乘法器的占用率大幅度降低,并降低了平均路径延时,这对信道化接收机的硬件实现是有利的。

4 结论

本文提出了一种无乘法器的数字信道化结构。利用CSD编码技术和改进动态旋转因子算法,对基于FRM的多相信道化接收机进行无乘法器优化。利用System Generator软件完成了数字信道化优化结构的设计和仿真,并对比和分析了无乘法器数字信道化结构和多相数字信道化结构在FPGA实现时的硬件资源占用情况。无乘法器优化后的数字信道化结构具有更低的延时与更低的乘法器资源占用率。