舰载ISAR成像平台运动补偿新方法研究

王 勇, 杨佳兴, 李亚军, 禄晓飞

(1.哈尔滨工业大学电子工程技术研究所,黑龙江 哈尔滨150001;2.上海无线电设备研究所,上海201109;3.中国酒泉卫星发射中心,甘肃 酒泉732750)

0 引言

ISAR具有全天时、全天候、观测距离远的优点[1],广泛应用于民用和军事领域[2-3]。我国海洋面积辽阔,海上防御系统意义重大,ISAR在海上防御系统中发挥着重要作用。海上防御系统中ISAR的主要形式是岸基ISAR,其在舰船目标成像中取得了很好的效果。

然而岸基ISAR受限于平台无法移动,观测距离有限,无法为远海海防提供支持。因此,舰载ISAR得以出现。相比于岸基ISAR,舰载ISAR具有支持远海海防的优势。同时,舰载平台自身的运动以及高海情下的三维摆动增加了ISAR成像的难度。

相较于岸基ISAR,舰载ISAR成像目前仍处于探索阶段。高悦欣等[4]对舰载ISAR舰船目标成像进行了仿真和建模,得出雷达平台自身的运动对成像基本无贡献,以及雷达平台三维摆动会对ISAR成像造成负面影响的结论。哈尔滨工业大学宿富林等[5]研究了舰载雷达平台三维摆动对ISAR成像的影响,得出雷达平台三维摆动幅度越大、周期越短,ISAR图像散焦越严重的结论。该课题组将基于时频分析的瞬时成像方法应用于舰载ISAR成像,图像质量得到了提升[6]。鲁静[7]提出基于图像对比度的成像时间段选取算法,提升了舰载ISAR图像质量。刘子滔[8]提出基于舰载雷达平台运动数据的雷达平台运动补偿方法,以此消除舰载平台运动对成像的影响。

在文献[8]中,用于构建舰载雷达平台运动补偿信号的平台运动数据通过姿态测量仪获得。然而由此得到的平台摆动数据精度不够,不能直接用来补偿雷达平台的运动。本文提出了基于回波进行平台运动补偿的舰载ISAR成像方法。相比于直接通过姿态测量仪获取运动数据,该方法能够获得更精确的舰载雷达平台摆动参数,进而更好地补偿平台摆动对成像的影响,提高图像聚焦性。

1 舰载ISAR回波信号模型

1.1 空间几何模型

舰载ISAR成像受舰船平台复杂运动的影响。舰船平台除存在自身运动外,由于海浪的作用,还存在偏航(yaw)、俯仰(pitch)、侧摆(roll)三个自由度的摆动。为更方便地表示目标和雷达之间的位置关系,建立三套坐标系:舰船坐标系o1xyz、摆动坐标系o1abd和惯性坐标系ouvw,如图1所示。其中,o1为舰船的重心,k为ISAR的重心,o2为目标的重心,q为目标的散射点。x轴平行于u轴,y轴平行于v轴,z轴平行于w轴。a轴与船体龙骨线平行,b轴垂直于船体侧面,d轴垂直于o1ab平面。偏航为舰船绕d轴转动,俯仰为舰船绕b轴转动,侧摆为舰船绕a轴转动,三种摆动均以逆时针方向为摆动正方向。

设舰船偏航、侧摆、俯仰的角度分别为θy(t)、θr(t)、θp(t),根据船舶动力学理论,它们可表示为

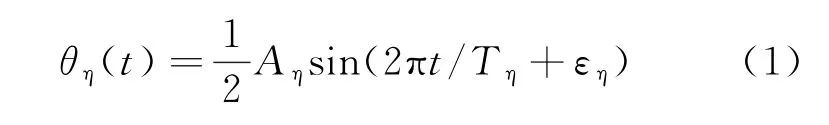
式中:η=y,r,p,分别表示偏航、侧摆和俯仰;Aη,Tη,εη分别表示摆动幅度、摆动周期和摆动初相。

此时,在舰船坐标系下舰船的偏航旋转矩阵可表示为[9]

舰船的侧摆旋转矩阵可表示为

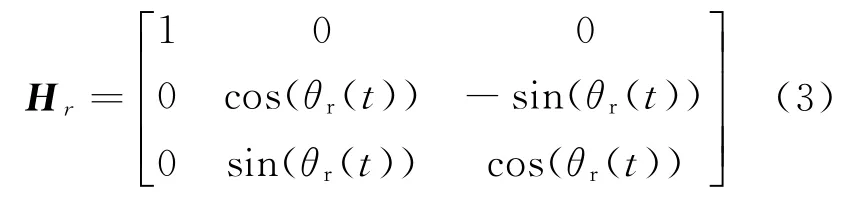
舰船的俯仰旋转矩阵可表示为

总的旋转矩阵可表示为

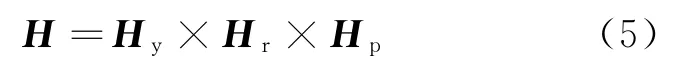
设初始时刻雷达重心k在摆动坐标系下的坐标为(ak,bk,dk),且摆动坐标系与舰船坐标系重合,则在t时刻,雷达在舰船坐标系下的坐标变为

设舰船重心o1在惯性坐标系下的坐标为(uo1(t),vo1(t),wo1(t)),则舰载雷达重心k在惯性坐标系下的坐标为

1.2 回波信号模型

ISAR通常采用线性调频(LFM)信号来获取高的距离分辨率,ISAR发射信号可表示为

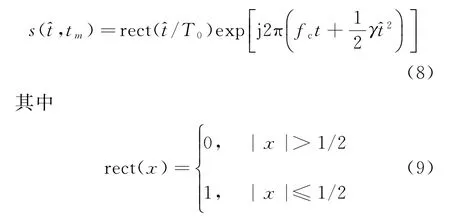
设目标散射点q在惯性坐标系下的坐标为(uq(t),vq(t),wq(t)),由文献[8]可知,tm时刻目标回波经过匹配滤波处理后可表示为

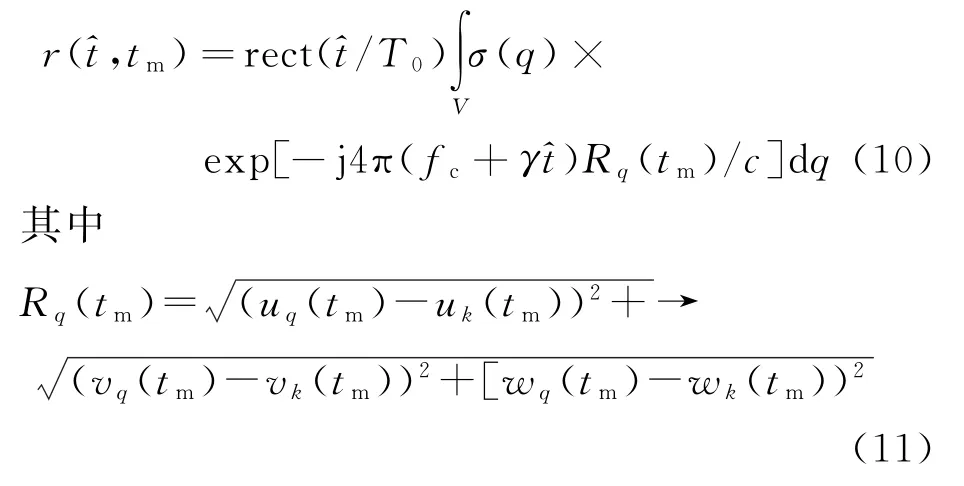
式中:V表示目标散射点的区域;σ(q)表示目标散射点q的散射强度;Rq(tm)为tm时刻目标散射点q到雷达的距离;c为光速。

由文献[8]可知ISAR成像基本满足平面波条件,此时Rq(tm)可表示为

式中:Ro1o2为o1、o2之间的距离;io1o2为o1o2方向的单位矢量;q表示矢量o2q;k表示矢量o1k。

则式(10)可表示为

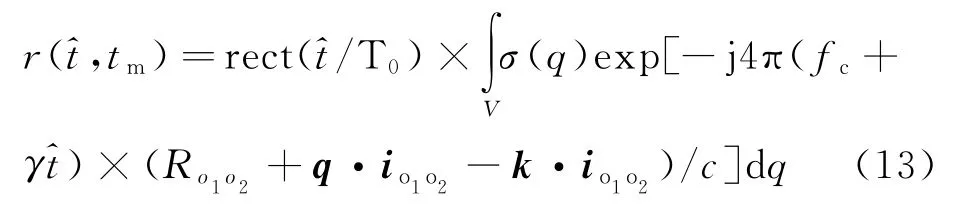
式(13)在经过包络对齐和相位校正后得到的信号可以表示为

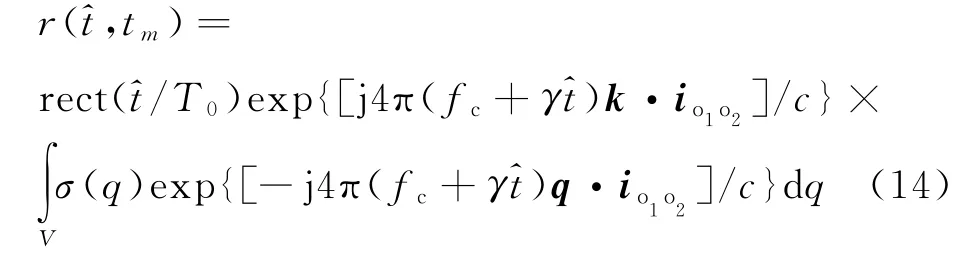
式(14)说明,在经过包络对齐和相位校正后,回波只受舰载雷达平台摆动分量及目标转动分量影响,且二者对回波的影响彼此独立。此时即可构建补偿信号,补偿信号定义为

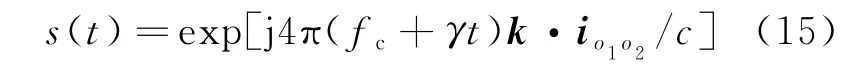
由式(15)可知,在获得雷达平台的三维摆动信息后,即可对雷达平台摆动进行补偿。由于舰载雷达平台自身的运动对成像的影响可通过包络对齐与相位校正消除,为方便表述,将后文中的雷达平台摆动补偿称为雷达平台运动补偿。

2 舰载雷达平台运动参数估计

2.1 平台摆动参数估计模型

由式(12)可知,目标自身运动和舰载雷达平台摆动对成像的影响互相独立,且舰载雷达平台摆动对所有散射点具有相同的影响。当目标存在三轴转动时,无法将目标的三轴转动等效到舰载雷达平台摆动上,否则目标的三轴转动将对所有散射点具有相同的影响,与实际情况不符。因此通过合适的方法即可从回波中获得舰载雷达平台的摆动参数。

当舰载雷达平台存在多维摆动时,由雷达平台运动产生的多普勒频率十分复杂,不易进行雷达平台运动补偿,且由于旋转矢量的变化,得到的ISAR图像质量不高。实际情况下,舰船一般通过船体控制装置对船体产生较大的阻尼,抑制舰船的偏航运动。由海浪引起的舰船俯仰摆动幅值一般很小,可忽略不计。故舰船只存在一维摆动的情况具有一般性。

因此可采用成像时间段选取技术,选取雷达平台只有一种摆动的时间区间,在此段时间内通过回波估计雷达平台运动参数并进行平台运动补偿和成像。由于摆动角度的初相与时间选取有关,可只对摆动角度的周期和幅度进行估计。为方便表述,将后文中摆动角度的周期和幅度称为摆动周期和幅度。设在惯性坐标系ouvw下目标重心o2的坐标为(u1,v1,w1),则由雷达平台侧摆引起的多普勒频率为

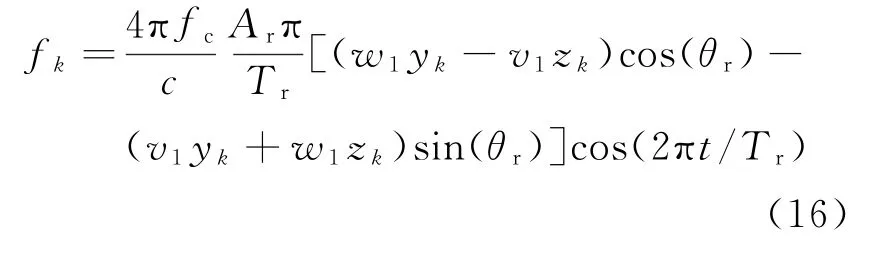
2.2 摆动周期估计

由式(1)及式(16)可知,当舰载雷达平台只存在一维摆动时,雷达平台摆动产生的多普勒频率具有周期性,且其周期与雷达摆动周期相同。估计摆动周期时,首先进行特显点距离单元的选取,其中选取的特显点距离单元对能量无特别要求,但其时频分布应含有雷达平台摆动周期信息。然后对选取的距离单元进行时频分析,得到时频分布。再进行时频脊提取,并对提取的时频脊做离散傅里叶变换(DFT),即可得到相应摆动周期的估计值。

为防止交叉项的出现,使用短时傅里叶变换(STFT)对选取的距离单元进行时频分析。回波信号r(n)的STFT表达式为

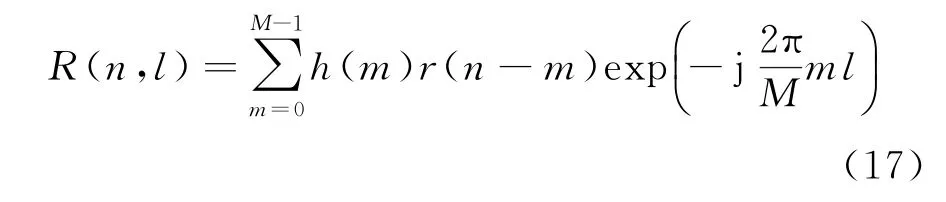
式中:h(m)为窗函数;M为窗函数宽度;l为频率点。

在获得回波信号的时频分布后,通过时频脊提取可得到各个时刻能量最大的频率分量,进而得出多普勒频率与时间的关系。时频脊提取表达式为

式中:fn为n时刻信号能量最大的频率分量;为获取使f(x)最大的x的函数。

在完成时频脊提取后,对提取的时频脊做DFT即可得到雷达平台摆动频率的估计值。摆动频率估计值表达式为

2.3 摆动幅度估计

由式(16)可知,回波信号的多普勒频率中包含着舰载雷达平台摆动的幅度和周期信息,其中多普勒带宽与雷达平台摆动的幅度有关。但由于多普勒带宽还受雷达位置等因素影响,加上时频分布分辨率等问题,不易直接从回波多普勒频率中提取舰载雷达平台摆动幅度。

由文献[8]可知,雷达平台摆动完全补偿后所得的ISAR图像,相比于不完全补偿所得的图像具有更好的聚焦性。故可结合估计出的摆动周期,对摆动幅值进行遍历,构建一系列补偿信号对回波进行补偿和成像。在获得相应ISAR图像后,以图像聚焦程度为标准,即可获得舰船摆动幅值的估计值。

由文献[7]可知,图像的聚焦程度可由图像熵来衡量。ISAR图像的聚焦越好,图像熵越小。图像熵表达式为

式中:g为M×N的图像;g(m,n)为图像灰度值;S为雷达图像总能量。

假设平台摆动幅度序列中第i个幅度为Ai,结合之前估计的摆动周期,可构建补偿信号si(t),表达式为

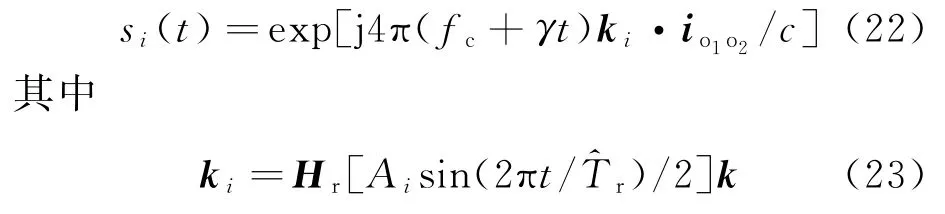
式中:ki为平台摆动幅度为Ai时雷达的瞬时位置矢量;为摆动周期的估计值;k为初始时刻雷达位置矢量。

利用si(t)对回波数据进行平台摆动补偿后,再进行ISAR成像,可得到相应的图像熵Ei。改变平台摆动幅度,重复以上运动补偿和成像过程,可获得一系列ISAR图像。此时,平台摆动幅度表达式为

式中:j为A在假设的摆动幅度序列中的位置;A为摆动幅度估计值。

利用上述方法可以得到舰载雷达平台的摆动周期与幅度的估计值。由此可构建雷达平台摆动补偿信号,进而得到聚焦良好的ISAR图像。相应流程如图2所示。

图2 舰载ISAR成像算法流程图

3 仿真验证

以飞机目标为例对本文所提出的雷达平台运动补偿方法进行仿真验证。不失一般性,这里假定目标匀速运动,舰载雷达平台只存在一维侧摆运动。目标与舰船均以惯性坐标系描述位置。初始时刻,摆动坐标系与舰船坐标系重合,舰船的重心在坐标系原点,雷达坐标为(0,0,30)。舰船侧摆摆动幅度为10°,摆动周期为2s,摆动初相为零。雷达发射线性调频信号,载频10GHz,带宽800MHz,脉冲宽度20μs,成像积累时间4s,脉冲重复频率1000Hz,距离维采样频率900MHz。目标散射点w轴坐标值相同,重心坐标为(10000,10000,60)。目标速度矢量与u轴夹角为60°,与w轴夹角为90°,大小为389m/s。由于目标匀速运动,无法确定准确的成像平面,将雷达视线与散射点航迹确定的平面近似为成像平面,目标散射点在近似成像平面上的分布如图3所示。

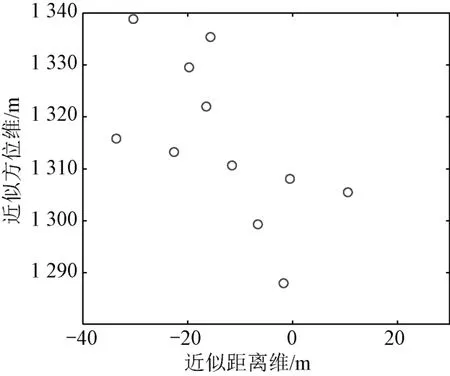
图3 目标飞机散射点模型

图4为目标散射点模型投影到成像平面后所成的ISAR图像。其中,距离维分辨单元为0.18m,方位维分辨单元为0.37m,后文图中分辨单元尺度不变。由于图3不是准确的成像平面,故图4与图3中的目标形状与尺寸存在一定差异,但仍可反映目标的轮廓信息。舰船无侧摆运动时,目标ISAR成像结果如图4(a)所示,ISAR图像可准确反映目标形状。图4(b)为舰载雷达侧摆运动时的成像结果,可知,舰载雷达的运动使ISAR图像散焦,部分散射点在距离维和方位维展宽。

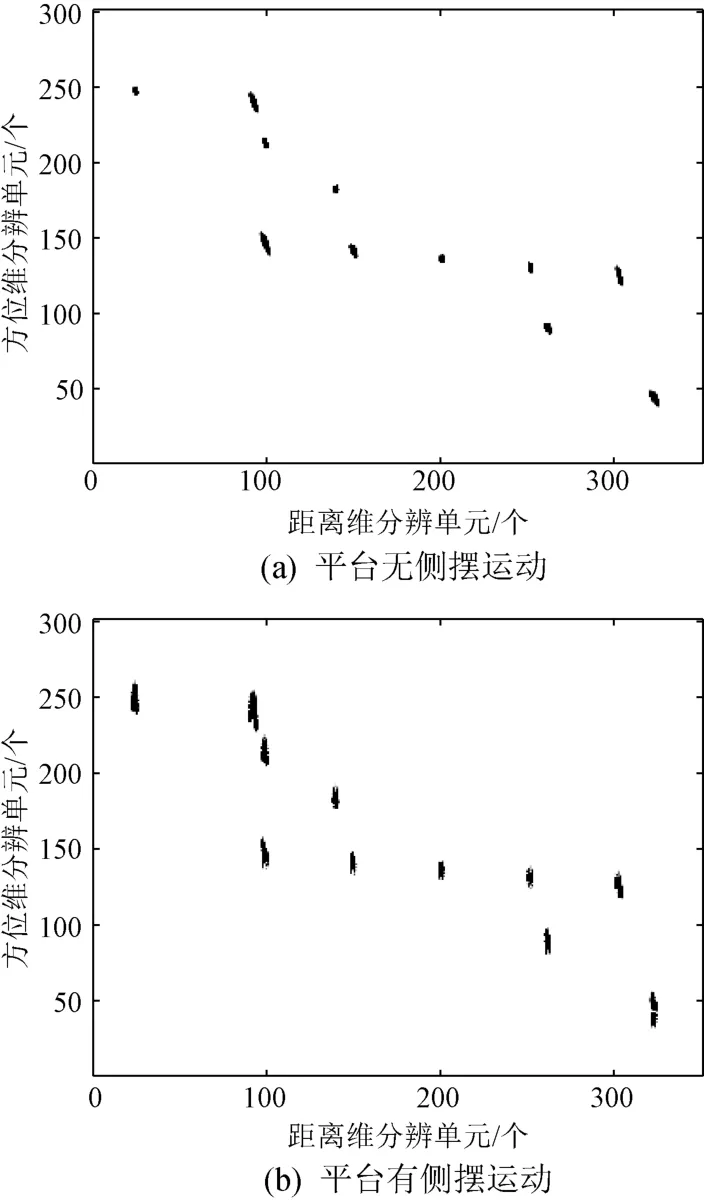
图4 目标ISAR图像

在舰船存在侧摆运动且回波信噪比为0dB时,进行目标一维距离像成像仿真。为更好地显示距离像,仿真结果只保留有距离像的部分,如图5所示。图5(a)为未经包络对齐和相位校正时的一维距离像,由相邻距离像在距离维的走动可知,目标存在大的平动分量,且舰载雷达平台存在正弦形式摆动。图5(b)为包络对齐和相位校正后的一维距离像。其中,包络对齐采用积累互相关法,相位校正采用恒定相位差消除法[10]。可见,经过包络对齐和相位校正后,目标平动及雷达平台摆动导致的一维距离像错位得到解决。

图6为所选取距离单元回波的时频分析结果。可见,当舰载雷达平台只存在一维摆动时,目标回波的多普勒频率具有周期性,且其周期与舰载雷达平台摆动周期相同。对图6进行时频脊提取,获得的结果如图7所示。可见,进行时频脊提取未改变相应多普勒频率的周期性。

对提取的时频脊进行DFT可得到的雷达平台摆动频率估计结果,如图8所示。其中,幅值最大的频率为摆动频率估计值,即,摆动频率的估计值为0.5Hz,摆动周期估计值为2s。可见本文所提方法能有效估计舰载雷达平台摆动周期。

利用平台摆动信息估计值构建补偿信号,对回波进行补偿后的成像结果,如图9所示。经过雷达平台摆动补偿后,图像聚焦性有所提高。

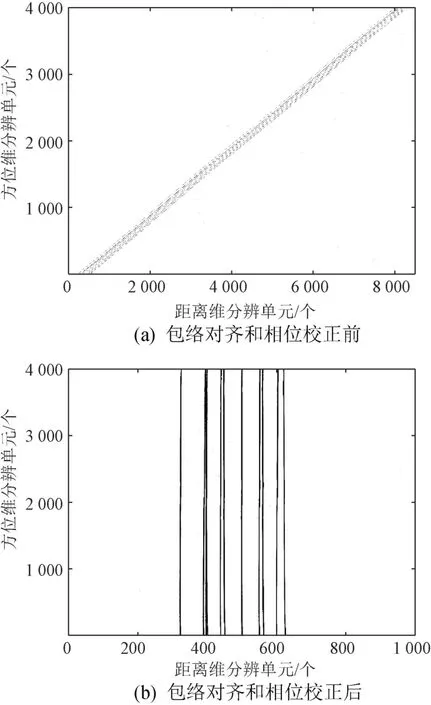
图5 目标一维距离像

图6 某距离单元回波时频分析结果

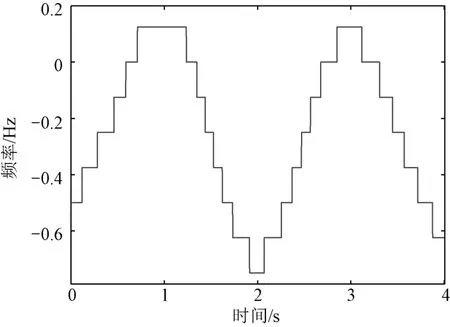
图7 时频脊提取结果

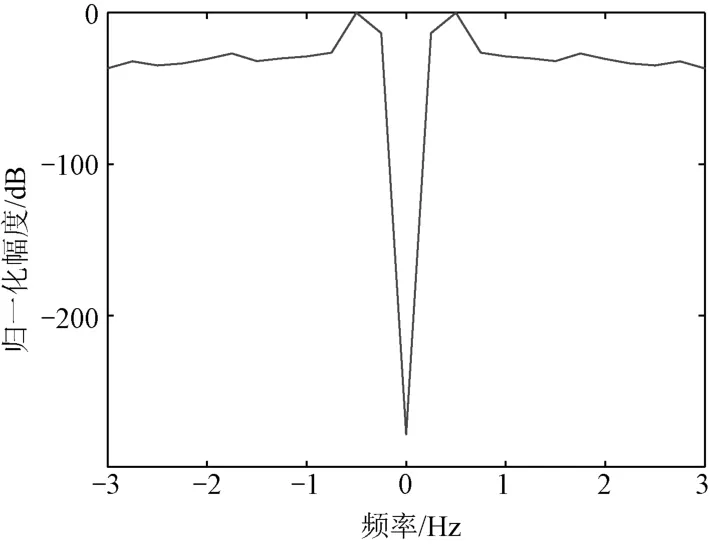
图8 平台摆动频率估计

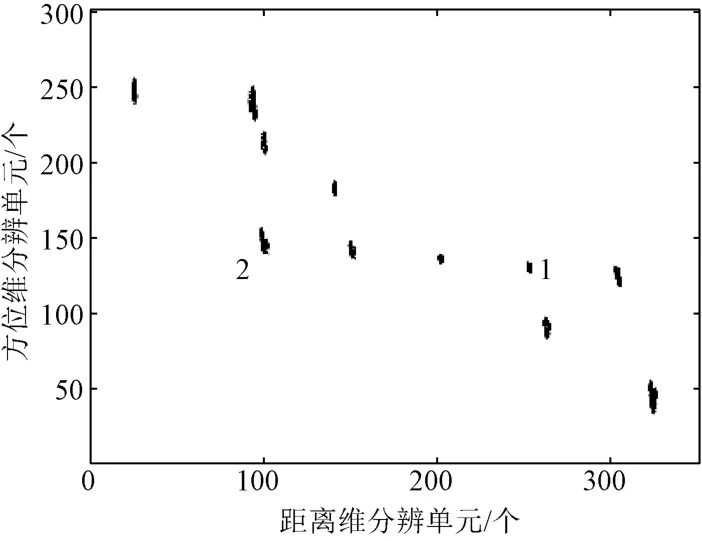
图9 平台摆动补偿后成像结果

对图9中散射点1、散射点2的方位维和距离维聚焦情况分别进行分析,如图10所示。经过摆动补偿后,目标散射点散焦情况得到改善。其中,中心点附近散射点散焦情况改善较为明显,部分远端散射点散焦情况改善效果虽不如中心点,但仍得到改善。

在当前参数下,舰载雷达平台无摆动、存在侧摆运动和经过摆动补偿三种情况下获得的ISAR图像熵分别为6.01,6.54和6.44。可见,舰载雷达平台侧摆运动时,所得ISAR图像的熵变大,图像聚焦性变差;而经过平台摆动补偿后,ISAR图像的聚焦性提高,相应ISAR图像的熵减小。

在其他仿真参数不变的情况下,改变回波信号信噪比,不同信噪比下的ISAR图像熵如表1所示。可见,本文所提出的舰载雷达平台摆动补偿方法可提高ISAR成像质量。

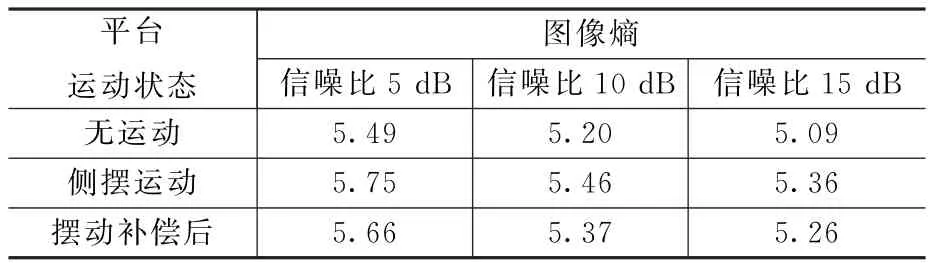
表1 不同信噪比ISAR图像熵

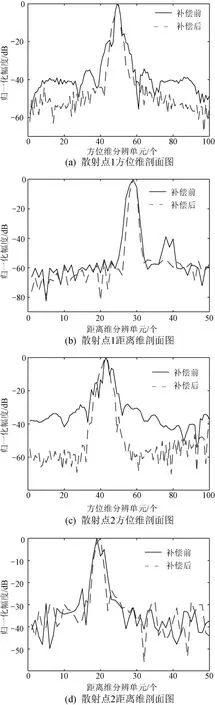
图10 散射点方位与距离剖面图

4 结论

本文对舰载ISAR成像中的舰船自身一维摆动补偿问题进行了研究。通过建模分析发现,回波数据的多普勒频率包含舰船摆动的信息。回波多普勒频率的周期只与舰船摆动周期有关,回波多普勒带宽与摆动周期、摆动幅度等因素相关。为了更好地对舰船摆动进行补偿,本文提出了一种通过提取回波数据时频脊获取摆动周期,并通过图像熵获取摆动幅度的方法。对仿真回波进行参数估计及舰船摆动补偿后,ISAR图像的聚焦性得到了有效提高。