三层复杂网络模型构建及特性分析
2020-12-22马海瑛肖玉芝赵海兴罗海秀
马海瑛,肖玉芝,赵海兴,吴 欢,罗海秀
(1.青海师范大学计算机学院,西宁 810016;2.青海省藏文信息处理与机器翻译重点实验室,西宁 810008;3.藏文信息处理教育部重点实验室,西宁 810008)
0 引言
网络科学经过15年的迅速发展,如今已经取得一系列丰硕的研究成果,也形成了一套完整、系统的理论体系和学科框架[1-10]。随着复杂网络的深入研究和发展,逐渐认识到单层网络已经不能准确地描述现实世界中的复杂关系,也无法解释现实社会中的多重复杂现象,因为,现实系统不是以单一,孤立的形式存在,而是各个系统之间相互交织,在结构和功能上相互依存、相互关联形成的复杂系统。故而近年来,复杂网络研究的热点内容逐渐转向多层网络[11-12]。多层网络的概念源于复杂网络中对“超网络”的研究,其侧重于刻画网络节点之间链接含义的多样化、权重的差异化特性。其研究使多个科学领域引起了广泛关注,如物理学、控制科学、计算机科学、社会学分别在各自领域的权威期刊上发表了多层网络的有关研究[13-20],展示了多层网络理论在相关学科中的应用。
多层网络研究中一个重要问题是了解网络拓扑结构特性,并进一步理解网络结构与动力学之间的关系。网络拓扑结构的改变与网络性能息息相关。为了深入理解网络的拓扑结构,首先需要构建网络模型,网络模型的构建常用的方法有两种,其一是源于现实世界存在的网络模型,其二是通过多层网络理论生成网络模型,再通过实证验证网络模型算法的可行性。
目前很多学者通过现实存在的网络模型进行网络性质分析,通过实证数据构建的模型使网络的结构(参数)更加确定。比如孙晓璇[21]等人构建了高铁-普铁交通双层复杂网络,第一层是高铁网络,第二层是普铁网络,基于构建的双层网络,分别分析了两个单层网络和双层网络的拓扑性质,并且以最大连通子图作为指标分析3个网络的可靠性,实验结果得出两层网络的可靠性介于高铁网络和普铁网络之间。伍杰华[22]构建了三层YouTube社会网络,其中节点为用户,边表示用户之间的交互关系,第一层是共享朋友关系,第二层是分享订阅关系,第三层是分享的影片关系。基于构建的模型,进行各子网之间的共性特征提取和各个子网自身的特性提取,提出一种基于迁移成分分析的多层社会网络层间链接算法,实验证明该迁移思想能够应用到多层次社交网络链接分类场景。张磊[23]等人从社交,内容,话题和观点4个方面构建了四层微博超网络模型,层内关系是各个子网中各要素之间的关系,层间关系是各个子网之间的联系,如某一用户发布一条微博,其内容关乎某一话题,且作者的情感倾向属于正向或是负向,以这些关系建立各层之间的连边,模型基础上运用关键节点识别的方法分析多层社会网络中个体的情感倾向。
刘强[24-25]等人通过理论算法建立了多层次超网络模型,文献[25]中基于小世界算法和无标度算法构建了4种三层超网络,层间连接关系采用随机连接和优先连接机制,分析了不同层间依赖关系下网络的拓扑指标,此外,提出了一种层次交叉度的概念,由实验结果得知,该指标能够有效衡量超网络的鲁棒性。文献[26]用非线性核的方法提出一种增长的模型,其中,多重层通过添加新链接和新节点来增长。研究表明,不断增长的多重网络模型也能在层间产生负相关。文献[27]中构建了双层ER网络和双层BA网络,在这两个模型之上,重点研究了节点在不同层间的关联度所起的作用。分析了一般网络的双连通性、误差和攻击容限以及相互连接性,涵盖了与多层网络相关的广泛的网络鲁棒性,发现多路复用层之间的相关耦合可以以不同的方式显著地改变多路复用网络的鲁棒性。从现有的多层网络研究成果可以看出,无论是通过实证研究网络内在机理,还是构建理论模型分析网络拓扑特性,都较为广泛地研究了网络的多个拓扑指标及其动力学行为。真实世界中存在很多三层网络模型,比如社交网络模型,基于“朋友关系-家庭关系-同事关系”构成的三层社交网络,又如城市交通网络模型,以“飞机场-火车站-高铁站”,城市代表网络中的节点,建立三层网络结构,并分析其鲁棒性等。现有的结果虽为多层网络的研究提供了一些新的方法和思路,但研究性质比较广泛。而本文重点研究网络层间连边概率对网络度分布的影响,试图寻找随机连边概率与网络拓扑结构之间的关联。
因此,基于以上背景,本文通过复杂网络理论构建三层网络模型,并对网络模型中层间、层内依赖关系进行深入、细化的研究。首先刻画并构建了3种三层复杂网络模型,层内分别采用随机、无标度和小世界生成算法,层间采用随机连接算法。从另外一种角度通过调整层内节点连边概率和层间节点连边概率,全面、深入地研究了网络层级关系对整个网络特性的影响。其次重点分类并对比分析了层内、层间连接概率变化对3种三层网络度分布的影响,网络的度分布特性与网络的平均度息息相关。最后探讨了3种三层网络的聚类系数和平均路径长度等指标,层内的连接关系对这些指标的影响并不大。研究结果从理论上为多层网络的研究打下一定基础。
1 三层网络模型构建
1.1 基本概念
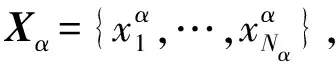
(1)
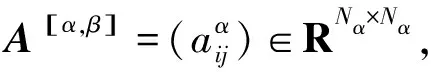
(2)
多层网络M的投影网络(projection network)为图proj(M)=(Xμ,Xμ),其中
(3)
1.2 三层网络模型演化算法
基于随机连接算法、无标度算法和小世界算法构造3种三层网络模型。根据多层网络的定义,三层网络M由集合g和层间连边C组成,其中g={Ga;a∈{α,β,γ}},Gα=(Xα,Eα)为网络层,层间连边C={Eαβ∈Xα×Xβ;Eβγ∈Xβ×Xγ}。通过随机概率定量刻画网络层间依赖关系,3种三层网络的演化过程如下:
1.2.1 网络EEE演化过程
网络层内依赖关系和层间依赖关系均采用随机连接算法,形成的网络简称为网络EEE,记为GΕΕΕ(N,p),该网络中不包含重复边。构造步骤如下:
第1步:初始条件,网络层Gα具有n个孤立节点,层内节点连边概率为p1(0,1),层间节点连边概率分别为pαβ(0,1)和pβγ(0,1),三层网络规模N=3n。
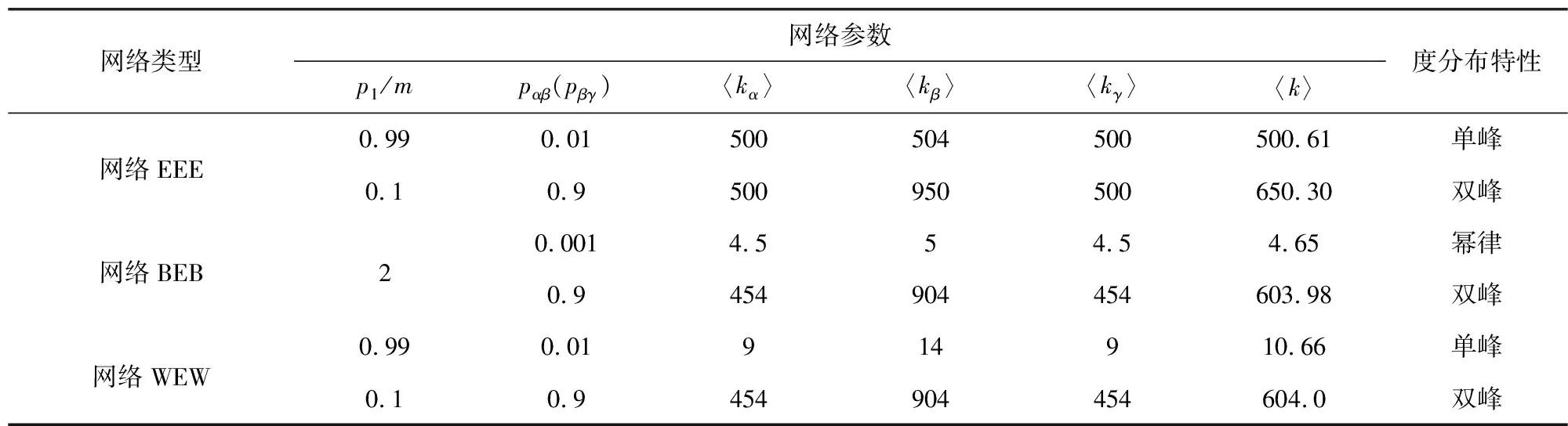
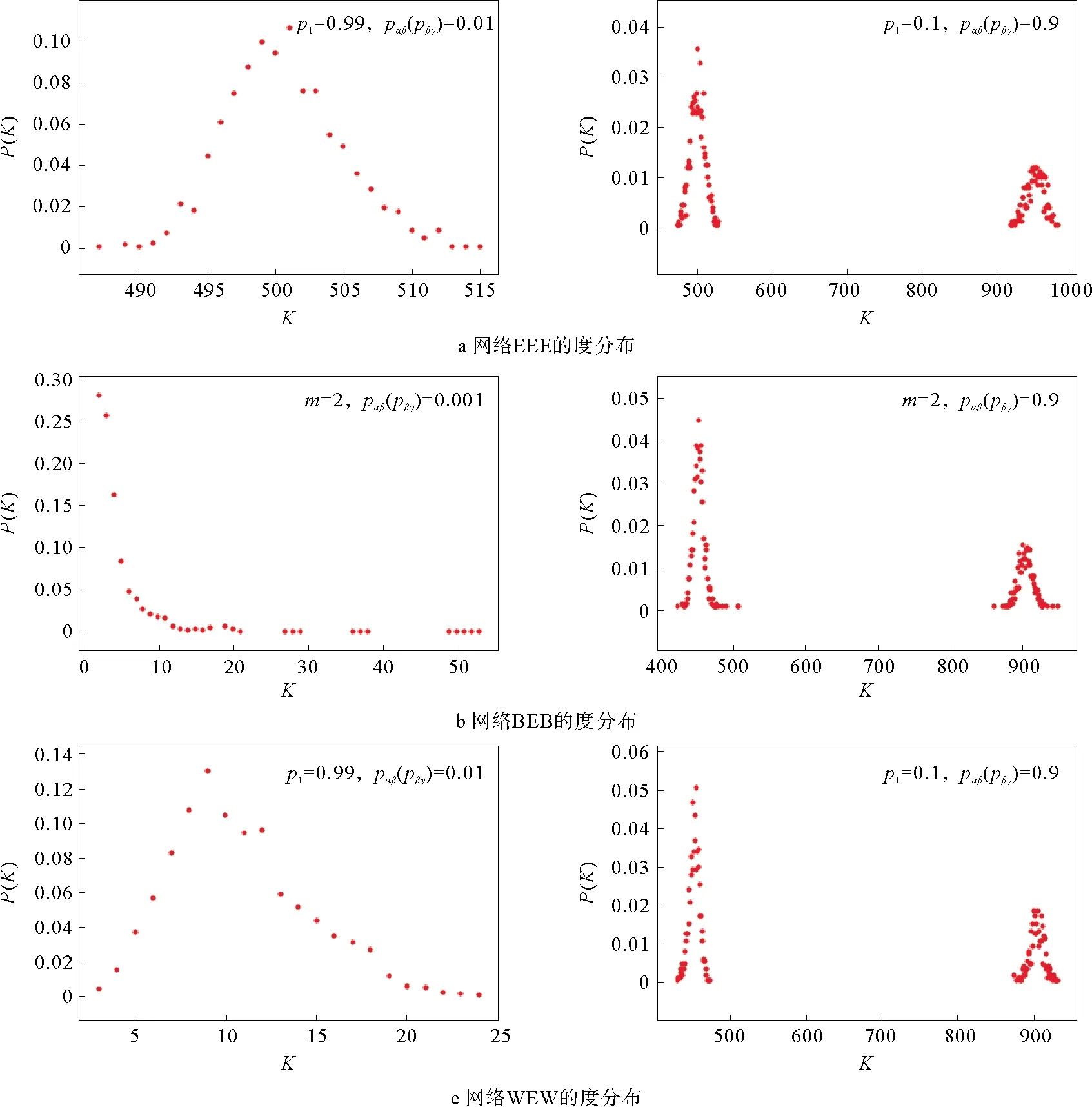
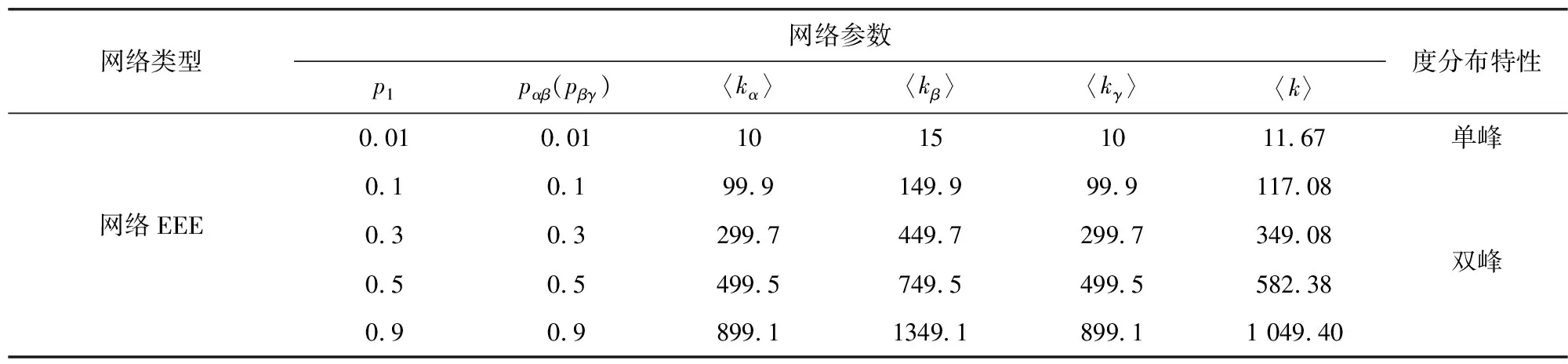
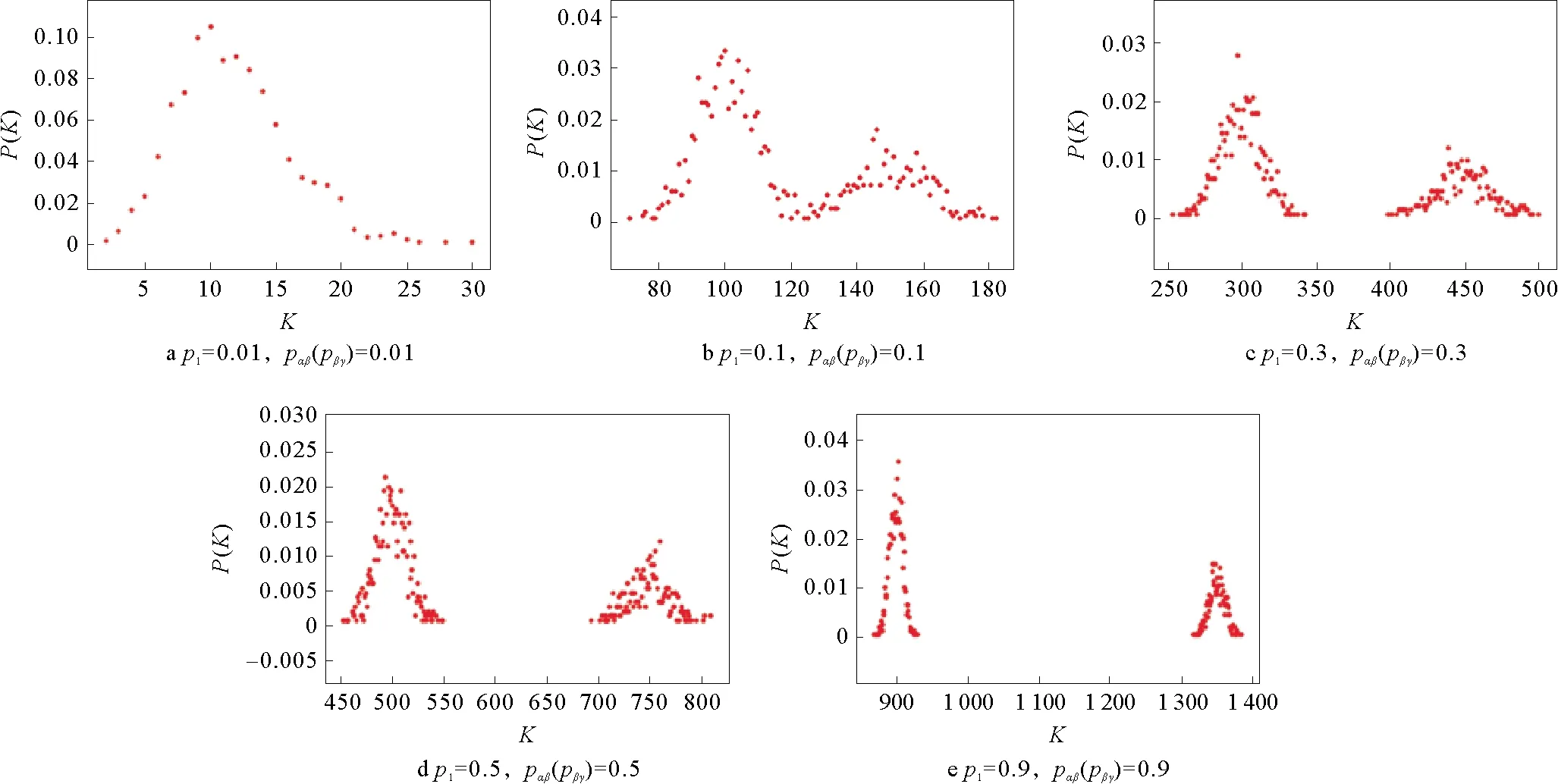
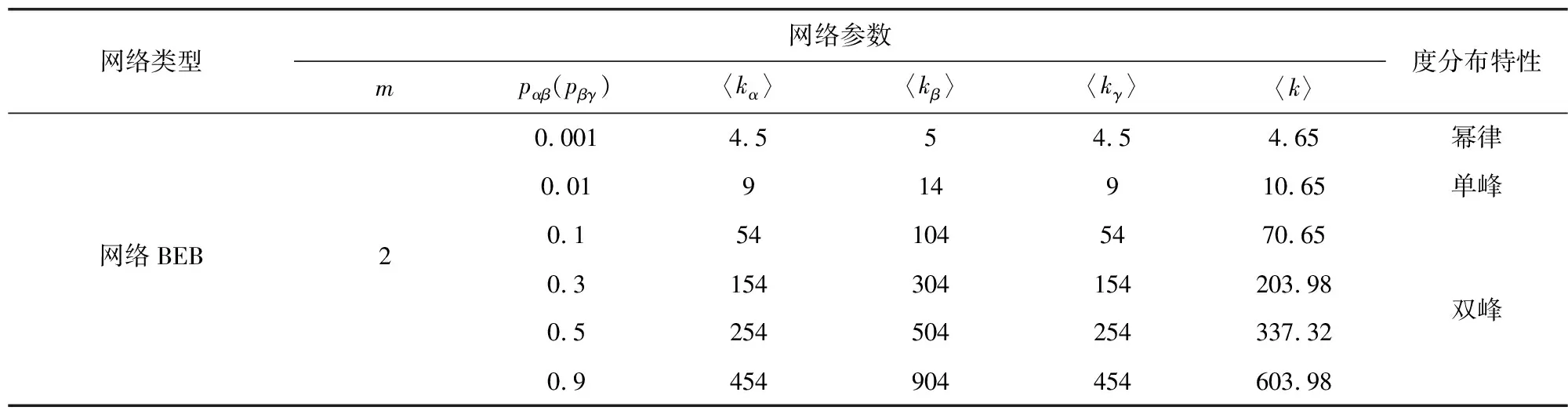
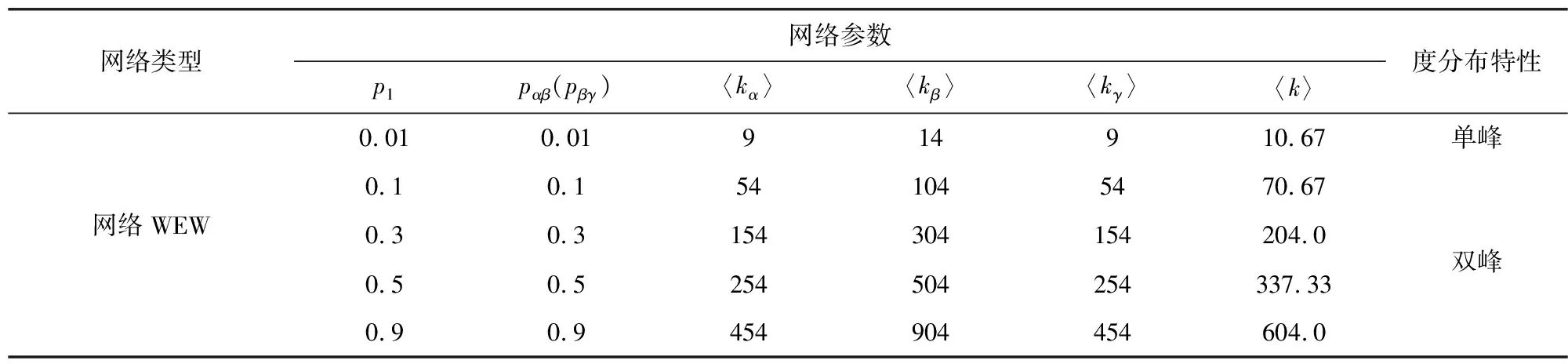
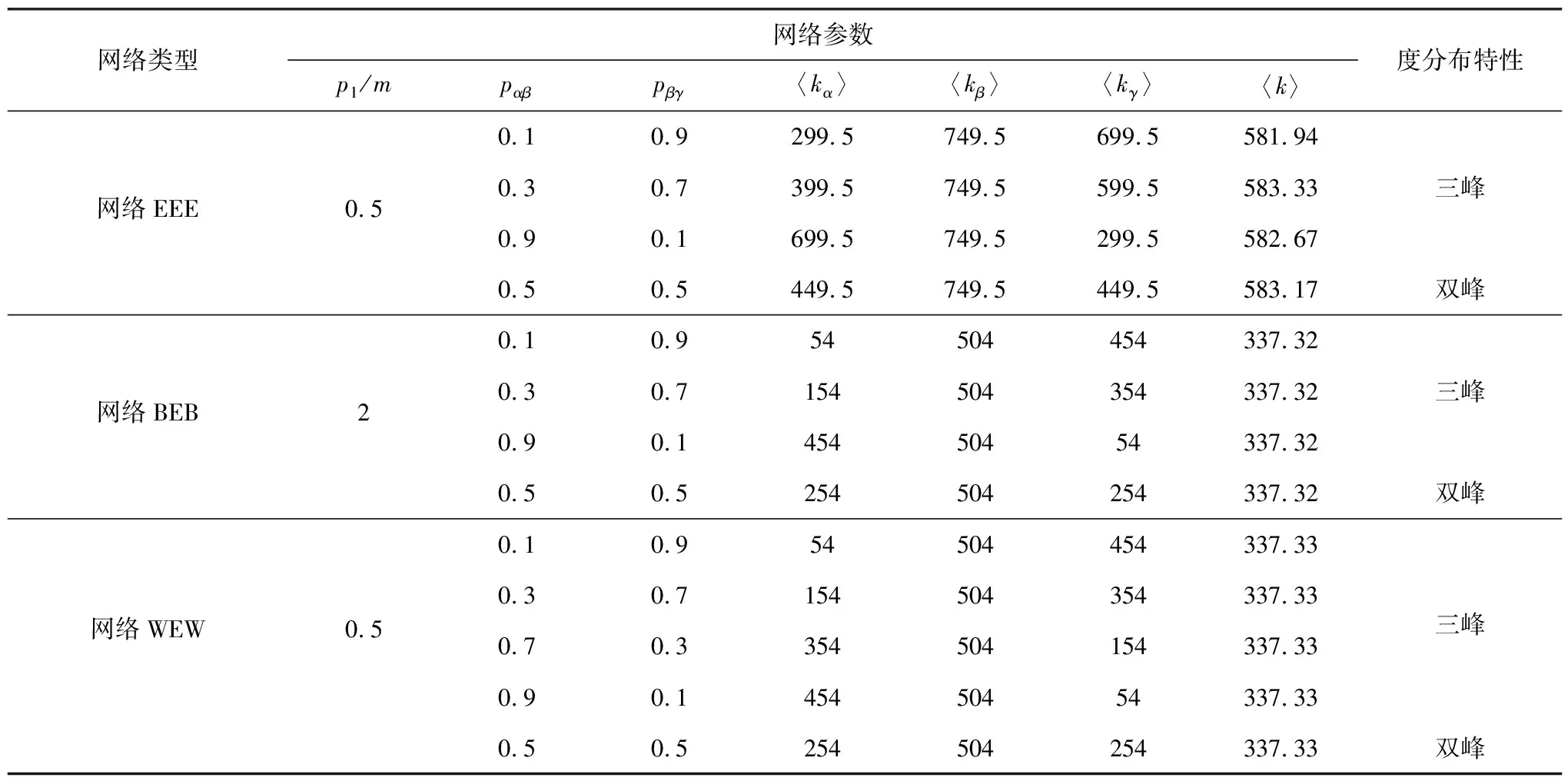
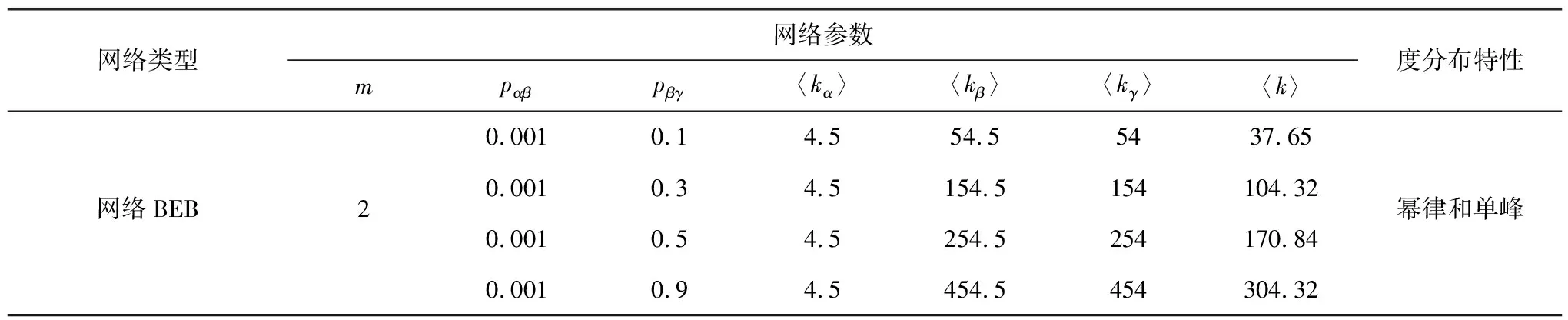
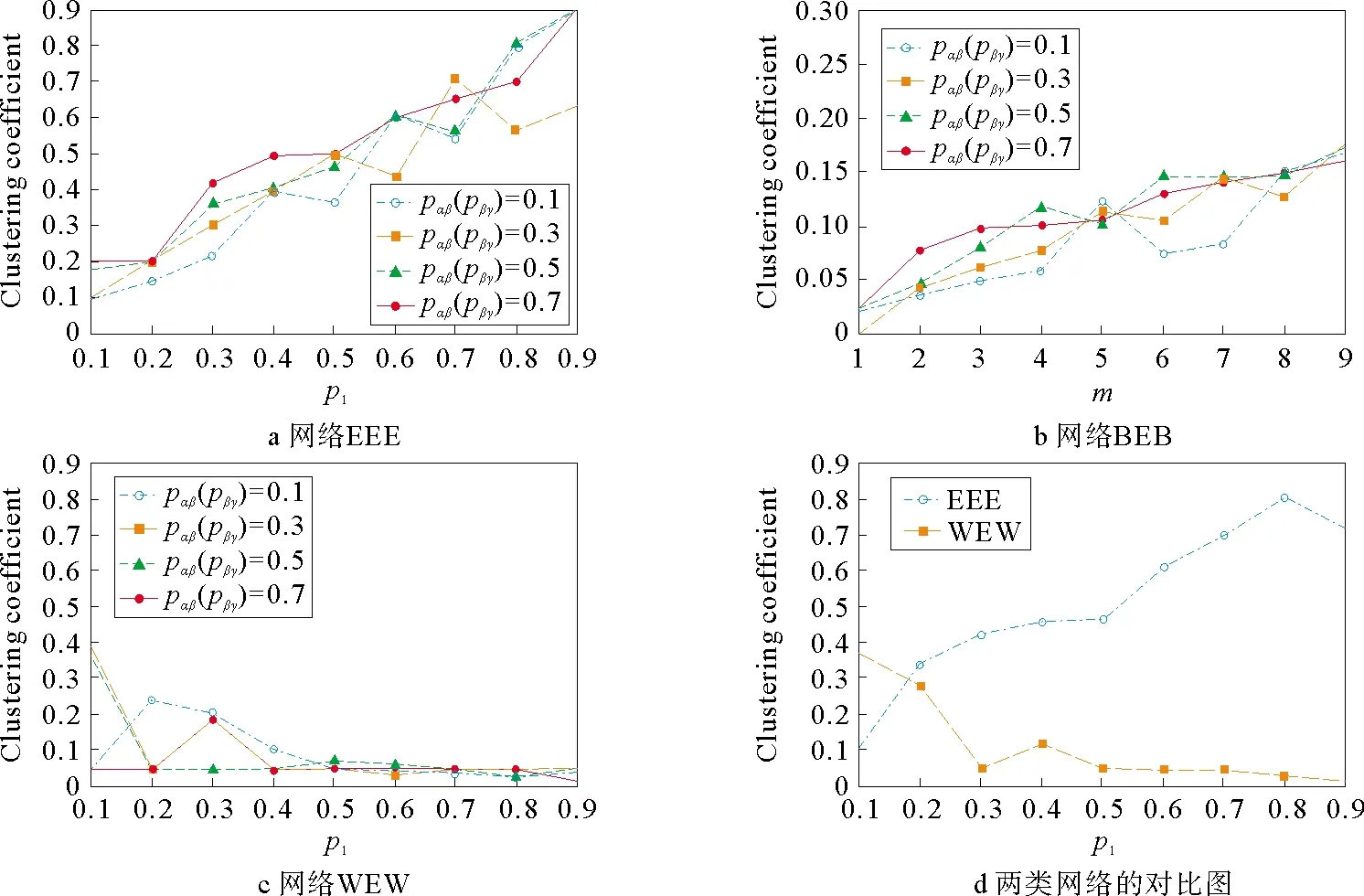
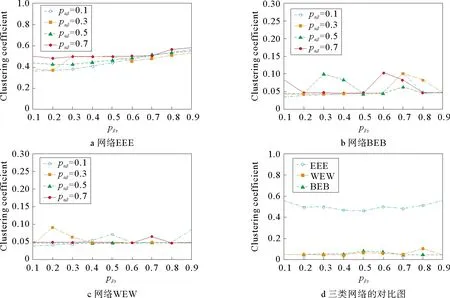
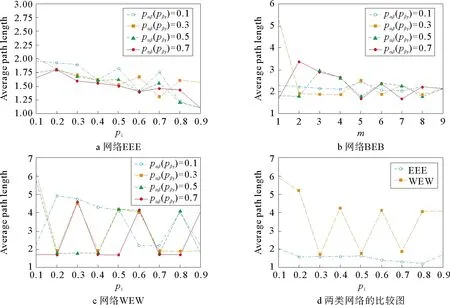
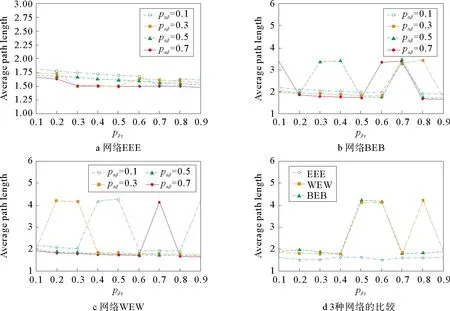
第2步:层内连接,网络层Ga中选择一对没有被选择过的节点,生成一个随机数r(0,1),如果r 第3步:复制网络层Gα,分别生成网络层Gβ和网络层Gγ。 第4步:层间连接,网络层Gα和网络层Gβ中选择一对没有被选择过的节点对,生成一个随机数m(0,1),如果m 1.2.2 网络BEB演化过程 层内依赖关系采用无标度算法,层间依赖关系采用随机连接算法,形成的网络简称为网络BEB,记为GΒΕΒ(N,m0,m,p),网络中不包含重复边。构造步骤如下: 第1步:初始条件,网络层Ga的规模为n,从一个具有m0个节点的完全图开始,每次引入一个新的节点和m(m 第3步:复制网络层Ga,分别生成网络层Gβ和网络层Gγ。 第4步:层间连接,网络层Ga和网络层Gβ中选择一对没有被选择过的节点对,生成一个随机数m(0,1),如果m 1.2.3 网络WEW演化过程 层内依赖关系采用小世界算法,层间采用随机连接算法,形成的网络简称为网WEW,记为GWEW(N,k,p),网络中不包含重复边。构造步骤如下: 第2步:层内连接,网络Ga层内以概率p1随机连接,即将边的一个端点保持不变,而另一个端点以概率p1变为网络中其余n-k-1个节点中随机选择的一个节点。任意两个不同的节点之间至多只能有一条边。 第3步:复制网络层Ga,分别生成网络层Gβ和网络层Gγ。 第4步:层间连接,网络层Ga和网络层Gβ中选择一对没有被选择过的节点对,生成一个随机数m(0,1),如果m 根据多层网络的定义及构造算法,图1给出了网络EEE的拓扑结构及其超邻接矩阵A。 图1 三层网络示意图 其中,Aα、Aβ和Aγ分别为三层网络的层内邻接矩阵。Aαβ表示第α层网络与第β层网络的层间邻接矩阵,Aβγ表示第β层网络与第γ层网络的层间邻接矩阵。由于第α层和第γ层之间没有连边,所以其相对应的邻接矩阵用0代替。矩阵A中的第1行表示网络层Ga中节点的度大小,第2行表示网络层Gβ中节点的度大小,第3行表示网络层Gγ中节点的度大小。 显然,三层网络节点的度值具有交叉性,极大地影响了整个网络的拓扑结构,使得网络的度分布出现多峰特性。为了深入研究层内节点连边概率和层间节点连边概率对网络拓扑结构和性质的影响,本文考虑了层间节点连边概率相同和层间节点连边概率不同的两种情形,分别分析了以上3种三层网络的度分布、聚类系数和平均路径长度等指标。 度分布是描述网络拓扑结构的重要参数,度分布P(k)为网络中度为k的节点占整个网络节点总数的比例,即: (4) 其中,Nk表示度为k的节点个数。 三层网络分别为Ga,Gβ和Gγ且层内节点连边概率为p1,网络层Gα和网络层Gβ之间的连边概率为pαβ,网络层Gβ和网络层Gγ之间的节点连边概率为pβγ。分别分析层间节点连边概率相同和不同时网络的度分布,即pαβ=pβγ和pαβ≠pβγ。 假设3种三层网络即网络EEE、网络WEW和网络BEB的单层网络规模和整个网络规模分别为n=500,N=1 500。 2.1.1 层间节点连边概率相同 本小节进一步对网络中的节点连边概率进行了细化和分类。假设网络层节点连边概率p1与网络层间节点连边概率pαβ(pβγ)之和为1;网络层节点连边概率p1与网络层间节点连边概率pαβ(pβγ)相等,即p1+pαβ(pβγ)=1和p1=pαβ(pβγ),下文进行详细分析。 1)第1种情形:p1+pαβ(pβγ)=1 当p1+pαβ(pβγ)=1时,实验中设置p1的取值范围为[0,1],pαβ(pβγ)的取值范围为[0,1],分别分析了3种三层网络的度分布特性,如表1和图2所示给出部分连接概率下的度分布情形。 表1 3种三层网络的度分布特性 图2 3种三层网络的度分布 表1中,〈kα〉表示网络层Gα的平均度,〈kβ〉表示网络层Gβ的平均度,〈kγ〉表示网络层Gγ的平均度,〈k〉表示整个三层网络的平均度。后文中的〈kα〉、〈kβ〉、〈kγ〉和〈k〉含义均与此处相同。 由图2可知,层间节点连边概率取值趋于1,层内节点连边概率取值趋于10-1时,由于中间层Gβ的节点的平均度〈kβ〉变大,网络层Gα和网络层Gγ的节点平均度值较小且相等,因此,表征出网络EEE和网络WEW的度分布具有双峰特性,即〈kα〉和〈kγ〉两部分叠加落到坐标轴左边形成左峰(第1个峰值);〈kβ〉形成坐标轴上的右峰(第2个峰值);层间节点连边概率取值趋于10-2,层内节点连边概率取值趋于1时,由于层间节点连边概率较小,网络层Gα、Gβ和Gγ的平均度几乎相同,因此,表征出网络EEE和网络WEW的度分布具有单峰特性;网络BEB的峰值变换与其他2种三层网络的度分布变换有差异,其层间节点连边概率取值趋于10-3时,网络表征出幂律分布。层间节点连边概率趋于1时,由于中间层Gβ的节点平均度〈kβ〉变大,网络层Gα和网络层Gγ的节点平均度值较小且相等,因此网络也表征出双峰特性。 因此,随着层间节点连边概率的增大,致使网络中间层的节点平均度也逐渐增大,所以,3种三层网络均呈现双峰特性。随着层间节点连边概率的减小,三个网络层的平均度值几乎相等,致使网络表征出单峰特性,且与构建单层网络的算法紧密相关,分别出现幂律特性和泊松分布特性。 2)第2种情形:p1=pαβ(pβγ) 接下来讨论层间节点连边概率与层内节点连边概率相同的情形即p1=pαβ(pβγ)。层内节点连边概率p1的取值范围为[0,1],层间节点连边概率pαβ(pβγ)的取值范围为[0,1]。为了表征出网络度分布的变换情形,本节实验中对3种三层网络分别进行讨论。 (1)网络EEE的度分布 网络EEE的三层网络分别为Gα,Gβ和Gγ,网络层节点连边和网络层间节点连边层均采用随机概率且随机概率值相等,表2和图3给出了部分概率下的网络度分布变换。 表2 网络EEE的度分布特性 图3 网络EEE的度分布 不难得出,随机连边概率趋于10-2时,网络度分布呈现单峰特性,即三层网络的平均度几乎相等。随着随机连边概率的逐渐增大,网络密度也随之增加,中间层的平均度迅速增大,使得网络度分布出现双峰形式。 (2)网络BEB的度分布 网络BEB中,网络层节点连边采用择优无标度算法,层间节点连边采用随机连接算法。因此,实验中只考层间节点连边概率的变换情况。 从表3和图4得出,网络层间节点连边概率趋于10-3时,网络BEB的度分布呈现出幂律特性;随机连边概率趋于10-2时,网络的度分布呈现单峰形式;随机连边概率趋于10-1时,网络的度分布出现双峰形式。随着随机连边概率的增加,中间层的节点平均度〈kβ〉逐渐增大且与网络层Ga和网络层Gγ的节点平均度之间的差值也逐渐增大,使得双峰之间的间隔逐渐增大。 表3 网络BEB的度分布特性 图4 网络BEB的度分布 (3)网络WEW的度分布 层内采用小世界生成机制,层间采用随机连边方式构造的网络WEW,表现出与网络EEE几乎相同的特性。 由表4和图5可知,层间节点连边概率趋于10-2时,网络WEW的度分布呈现单峰特性;层内节点连边概率与层间节点连边概率取值范围满足p1=pαβ(pβγ)=[0.3,0.9]时,网络的度分布均呈现双峰特性,随着p1和pαβ(pβγ)的增加,网络层Ga的平均度〈kα〉和网络层Gγ的平均度〈kγ〉比网络层Gβ的平均度〈kβ〉小,变现出双峰间隔较远。 表4 网络WEW的度分布特性 图5 网络WEW的度分布 2.1.2 层间节点连边概率不同 本小节深入分析了3种三层网络模型构建中层内节点连边概率和层间节点连边概率均不同的情形。网络EEE和网络WEW中层内节点连边概率p1=0.5,层间节点连边概率pαβ和pβγ的取值范围分别为[0,1]且约定pαβ+pβγ=1,网络BEB中层内采用无标度算法(m=2),层间节点连边概率与其他2种网络取值范围一致。 从图6~8和表5可知,当网络层Ga和网络层Gβ之间的节点连边概率pαβ在10-1到100,即网络层Gβ和网络层Gγ之间的节点连边概率pβγ在100到10-1时,三层网络的平均度分别为〈kα〉、〈kβ〉和〈kγ〉,其值均不相同,3种三层网络的度分布均出现三峰形式,〈kα〉为第1个峰值,〈kβ〉为第2个峰值,〈kγ〉为第3个峰值。特别地,当层间节点连边概率pαβ=pβγ=0.5时,网络便现出双峰特性,与2.2.1的结果相同。两个网络层之间的联系程度越紧密,对应网络层的节点平均度值越相近,如图6~8所示,两个峰值间隔就越小。 表5 3种三层网络的度分布特性 图6 网络EEE的度分布 图7 网络BEB的度分布 图8 网络WEW的度分布 另外,我们还分析了层间节点连边概率pαβ和pβγ之和不等于1时网络BEB的度分布。通过调整pαβ的值,网络的度分布会呈现出幂律和单峰同时存在的情况,如表6和图9所示。 表6 网络BEB的度分布特性 图9 网络BEB的度分布 为了使网络层Gα和网络层Gβ之间的联系程度较小,则层间节点连边概率取值趋于10-3时,网络层Gα保持了无标度网络的幂律特性,随着网络层Gβ和网络层Gγ之间节点连边概率pβγ的逐渐增加,〈kβ〉和〈kγ〉的值几乎相等,重叠形成右峰。 综上所述,通过实验仿真得出,三层网络层内节点连边概率对整个三层网络的影响较小,如果层间节点连边概率较小,网络度分布表现出单层网络的度分布特性;如果层间节点连边概率较大,三层网络的两个层间级的连边概率取值相同时,网络度分布表征出双峰特性,即第一层网络和第三层网络的平均度值相等,在度分布图中叠加成一个峰,中间层的平均度值另成一个峰;三层网络的两个层间的连边概率取值不相同时,网络度分布表征出三峰特性,独立网络层的平均度值大小不相等,在度分布图中各自成峰,并且层间联系程度密切的两个网络层的平均度值差较小,度分布图中表现出两个峰连接紧密。 网络的拓扑结构决定着网络的功能,度值从局部表征了网络的拓扑结构,接下来从全局分析本文提出的3种三层网络的功能。 聚类系数的统计分布是刻画网络的一个重要特征,其反映了网络中各节点之间的聚集程度,对网络整体性质进行了量化,其计算公式为 (5) 其中,T(i)表示节点i包含的三角形个数,deg(i)表示节点i的度。 本节分析了层间节点连边概率相同(不同)时3种三层网络的聚类系数。假设层内节点连边概率为p1(0 2.2.1 层间节点连边概率相同 根据式(5)得到3种三层网络聚类系数的变换趋势图。当pαβ=pβγ且p1=(0,1)时,3种三层网络的聚类系数变化曲线为图10a~c。当pαβ=pβγ且p1=1-pαβ(pβγ)时得到如图10d所示网络WEW和网络EEE的聚类系数。 不难得出: 1)当层间节点连边概率相同(pαβ=pβγ),且随着其值的逐渐增大,网络EEE的聚类系数比网络WEW的聚类系数更容易受到层内节点连边概率p1的影响,如图10a和10b所示,CEEE=[0.1,0.9],CWEW=[0.05,0.4],特别地,当层间节点连边概率pαβ(pβγ)=0.5且p1>0.2时,网络WEW的聚类系数趋于稳定。网络BEB的聚类系数随m的增加而增加(图10c),较大的层间节点连边概率pαβ(pβγ)也会使网络的聚类系数有所增长,但是增长的幅度并不大,网络的聚类系数取值范围为CBEB=[0,0.15]。 图10 三层网络的聚类系数 2)当层间节点连边概率相同(pαβ=pβγ)且与层内节点连边概率满足p1+pαβ(pβγ)=1时,网络EEE的聚类系数仍然与p1成正比,而网络WEW的聚类系数与p1成反比,此时增加层间节点连边概率,减小层内节点连边概率时,网络WEW才会出现相对较高的聚类系数。 2.2.2 层间节点连边概率不同 本节从另一视角(层间节点连边概率不同)对比分析3种三层网络的聚类系数。假设层内节点连边概率p1=0.5,m=2,pαβ≠pβγ,由式(5)计算得到3种三层网络的聚类系数的变化曲线如图11a~11c所示。 如果约定pαβ+pβγ=1,则得到如图11d所示的3种三层网络聚类系数的变化曲线。 图11 三层网络的聚类系数 不难得出: 1)随着层间节点连边概率pβγ和pαβ逐步增加,网络EEE的聚类系数也随之增加,而网络BEB和网络WEW的聚类系数的变化相对较小,CEEE=[0.39,0.57],CBEB=[0.0,0.1],CWEW=[0.04,0.1]。 2)当pαβ+pβγ=1时,网络EEE的聚类系数依然变现出较大的值,而其他2种网络的聚类系数相对较小,无论增加pβγ的值还是增加pαβ的值,网络WEW和网络BEB的聚类系数几乎相同且处于稳定状态。 因此,通过增加层间和层内节点连边概率,网络EEE的聚类系数会大幅度增加,而其他2种网络的聚类系数增加的较慢,也得出层间节点连边概率相比于层内节点连边概率对网络的聚类系数的影响较小。 平均路径长度可以衡量网络的传输性能和效率,它反映了网络中任意两点之间的距离,计算公式为 (6) 其中,dij为两节点i和j之间的最短距离。 网络的平均路径长度能从另一个角度很好地刻画网络的结构与特征,进而对网络有更深入的研究。本节将从层间节点连边概率相同和层间节点连边概率不同两种情形下,多角度、多方式对比分析网络EEE,网络BEB和网络WEW的平均路径长度。本节中,实验设置和网络规模见2.2。设网络EEE、网络WEW和网络BEB的平均路径长度分别为LEEE,LWEW和LBEB。 2.3.1 层间节点连边概率相同 本小节在层间节点连边概率相同(pαβ=pβγ)时,分析三层网络的平均路径长度的变化情况。 根据式(6)得到3种三层网络的平均路径长度的变化趋势如图12a~12c所示。当pαβ=pβγ且p1+pαβ(pβγ)=1时,得到网络EEE和网络WEW的平均路径长度的变化曲线如图12d。 由图12可知: 图12 三层网络的平均路径长度 1)网络EEE的平均路径长度随层内节点连边概率p1和层间节点连边概率pαβ的增加而减小,其变化范围为[1.1,2],相比于其他两种网络,有明显的减小趋势;而网络BEB和网络WEW相对稳定,但网络WEW的平均路径长度变化范围比BEB大。网络BEB的平均路径长度随m增加逐渐趋于稳定,在m=1且pαβ=0.3时有最大值LBEB=5.3,m=5后在[1.7,2.5]范围内小幅度变化;网络WEW的平均路径长度变化幅度较大,其变化范围为[1.8,6],层间节点连边概率pαβ=0.7,层内节点连边概率p1=0.1时,网络WEW的平均路径长度为最小值1.8,当p1=0.9时,LWEW=4.3。层间节点连边概率pαβ=0.1,层内节点连边概率p1=0.1时,LWEW=2.2;当p1=0.9时,LWEW=2.2。当层间节点连边概率pαβ=0.3,层内节点连边概率p1=0.1时,网络WEW的平均路径长度有最大6.2,p1=0.9时,LWEW=1.8。当层间节点连边概率pαβ=0.5,层内节点连边概率p1=0.1时,LWEW=5.7,当p1=0.9时,LWEW=1.8。因此,相比于其他两种网络,网络WEW的平均路径长度更容易受层内节点连边概率和层间节点连边概率的影响。 2)当p1+pαβ(pβγ)=1时,网络WEW的平均路径长度变化幅度仍然较大,表现出复杂的变化趋势;网络EEE的平均路径长度相比网络WEW变化幅度较小,相对稳定,且其值小于网络WEW。 2.3.2 层间节点连边概率不同 本小节在层间节点连边概率不同(pαβ≠pβγ)时,对比分析了三层网络的平均路径长度变化情况。 根据式(6)计算得到如图13a~13c所示的变化曲线。假设pαβ+pβγ=1,则3种三层网络的平均路径长度如图13d所示。 图13 三层网络的平均路径长度 实验仿真得出如下结果: 1)层间节点连边概率不同(pαβ≠pβγ),且随层间节点连边概率pβγ和pαβ的增加,网络EEE的平均路径长度减小,变化范围比其他两种网络都小,网络WEW的平均路径长度变化范围最大。LEEE=[1.52,1.82]。网络BEB的平均路径长度在pβγ=0.6之前随pαβ的增加而减小,pβγ=0.6后变化幅度较大,LBEB=[1.63,3.45]。网络WEW的平均路径长度变化相对复杂,当层间节点连边概率pαβ=0.1,pβγ=0.1时,LWEW=2.2,当pβγ=0.9时,LWEW=4.2。当层间节点连边概率pαβ=0.3,pβγ=0.1时,LWEW=2.02,pβγ=0.9时,LWEW=1.7。在pαβ=0.5和pαβ=0.7时随pβγ的增加处于平稳状态。由此可见,层间节点连边概率pβγ和pαβ的增加,使网络WEW的平均路径长度比另外两种网络更容易被影响。 2)当pαβ+pβγ=1时,网络EEE的平均路径长度相对稳定;网络BEB和网络WEW的平均路径长度曲线表现出复杂的变化情况,这两种网络的平均路径长度值几乎相等,直至pβγ=[0.7,0.9],网络WEW的值大于BEB。此外,网络EEE的平均路径长度值比其他两种网络的平均路径长度值小。 综上所述,随层内节点连边概率和层间节点连边概率的增加,网络EEE的平均路径长度减小,表明其平均路径长度容易受到层内节点连边概率的影响;网络BEB的平均路径长度变化幅度较小,但其更容易受层间节点连边概率的影响;网络WEW的平均路径长度变化幅度较大,层间连接概率和层内节点连边概率均会使其平均路径长度变现出较大的变化趋势。 本文基于经典的随机算法、无标度算法和小世界算法构造了3种三层网络模型,层间依赖关系采用随机连接算法。深入研究和刻画了层内依赖关系和层间依赖关系对3种三层网络结构和特性的影响。基于本文的实验,我们得出如下结论:1)三层网络中第一层网络和第二层网络的层间节点连边概率与第二层网络和第三层网络的层间节点连边概率相同且连边概率取值较小时,3种三层网络的度分布均保持单层网络的度分布特性;层间节点连边概率取值较大时,3种三层网络的度分布均呈现双峰特性。2)三层网络中第一层网络和第二层网络的层间节点连边概率与第二层网络和第三层网络的层间节点连边概率不相同时,3种三层网络的度分布均呈现出三峰特性;当层间节点连边概率取值较小时,网络BEB中出现幂律和单峰同时存在的度分布形式。3)层内节点连边概率对网络EEE的聚类系数影响相对较大,层间节点连边概率对3种三层网络的聚类系数影响较小;层间节点连边概率对网络EEE和网络BEB的平均路径长度影响较小,对网络WEW的平均路径长度影响较大。基于本文构造的3种三层网络模型后续可以探讨网络层数和其他参数对网络其他性质的影响,如鲁棒性、同步、传播等。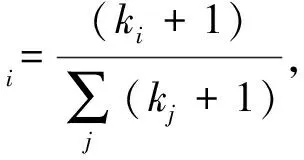
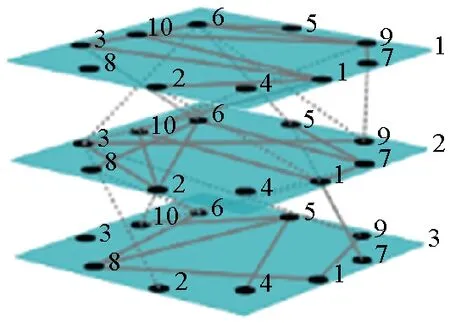
2 实验结果及分析
2.1 三层网络度分布





2.2 三层网络的聚类系数
2.3 三层网络的平均路径长度
3 结论
