基于LDA主题模型的用户特征预测研究

王雅静，郭 强，邓春燕 ，林青轩 ，刘建国

(1.上海理工大学复杂系统科学研究中心,上海 200093；2.上海财经大学会计与财务研究院,上海 200433；3.新浪微热点大数据研究院,上海 210204)

0 引言

用户特征是分析网络用户的重要途径，它可以基于用户行为以及建立模型实现预测[1]，在了解用户个体的同时也能够提高社交平台的信息服务质量，近年来通过用户各种行为推断用户特征、实现应用的相关研究[2-4]也逐渐增多。而点赞行为相较其他用户行为更简单直接，它能直接体现用户对某事件是否持有赞同态度，并且同样能够实现用户特征的预测[5-6]。文献[7]曾通过Facebook上在线用户的点赞标签进行奇异值分解(SVD)和Logistic回归，预测用户特征和属性。SVD优点在于可以忽略用户的主题偏好，直接利用点赞行为进行特征预测。但由于无法保证SVD的鲁棒性，预测新数据时需要重新构建矩阵进行计算，然而实际问题中通常面临百万级别以上的数据，此时再通过SVD计算的代价很大，因此难以实现新数据的预测。该场景下考虑用户点赞的主题特征更有效。

微博作为当今流行的社交平台，成为了各领域的研究热点。由于用户发表的短文本标签一般由微博平台提供，用户在微博上发生的点赞行为可以视作用户个人偏好的具体体现，但并非所有已有标签均能够准确地体现用户真实偏好[8]。若能将主题模型与用户点赞行为相结合，利用主题模型挖掘用户点赞信息的隐含主题，不仅能够更好地表达用户真实偏好，当新数据加入时，新数据中用户点赞信息的主题分布还能够由训练好的主题模型判断得到，进而实现新用户的特征预测。主题模型是挖掘文本主题的重要工具。

主题模型常用于自然语言处理与机器学习中，通过发现文档中核心主题，可以有效避免忽略文档的词背后隐藏的语义信息[9]。由于微博短文本的特性，为了降低在主题提取过程中微博信息的稀疏性和多维性造成的影响，可以选择基于语义分析的模型挖掘微博主题[10]，常见语义分析文本挖掘模型有LSA(Latent Semantic Analysis)、PLSA(Probabilistic Latent Semantic Analysis)和LDA，其中LSA需要大量文档以及词汇提升结果，PLAS存在过拟合问题[11]，而LDA主题模型虽属于无监督模型，但模型能根据已有语料库训练进而划分新文本主题，并且能够克服标签局限性以及语义模糊性、缓解数据多维性和稀疏性等问题[12]，因此在微博主题提取中，LDA主题模型被广泛应用。文献[13]通过LDA模型提取隐含主题特征；文献[14]使用LDA模型挖掘用户潜在兴趣主题。

本文的主要贡献为：1)实验中通过LDA主题模型对用户点赞文本集合进行主题挖掘，用一致性系数判断最佳主题数，实现主题划分，实验结果显示，基于主题预测用户特征相较基于微博标签SVD的F1值最高提升0.15，一定程度上反映了主题挖掘更能体现用户的真实偏好，帮助平台更加了解用户群体；2)提出了一种预测新用户特征的研究方法。利用已训练好的主题模型直接对新加入的数据进行用户特征预测，避免了SVD预测过程中仍需重新计算的弊端，为用户特征分析提供了另一条可行途径。

1 基于SVD分解的用户特征预测模型

1.1 SVD分解

本文实验中，以基于SVD分解的传统预测模型作为对比方法。SVD算法是一种矩阵分解算法，假设矩阵A∈R是一个a×b的矩阵，则定义矩阵A的SVD分解为：

(1)

其中，U∈R是a×a的正交矩阵，U的列向量称为左奇异值向量；Σr=diag(λ1,λ2,…,λr)，对角线的值为矩阵A的非零奇异值，r=rank(A)；V∈R是b×b的正交矩阵，VT是V的转置，V的列向量称为右奇异向量。一般可用最大的k个奇异值和相应的左右奇异值向量近似描述矩阵，即：

(2)

2.2 Logistic回归模型

Logistic回归是经典的二分类模型，其主要思想是：利用现有数据，在分类边界线上构建回归公式，进而实现分类和预测[16]。Logistic回归由条件概率P(Y|X)表示，随机变量X取值为实数，随机变量Y取值为0或1。参数一般通过训练数据确定模型，进而实现预测。二项Logistic的条件概率分布如式(3)所示。

(3)

(4)

SVD分解后的矩阵以及对应的用户特征作为训练集输入Logistic回归模型，进而实现对新数据的预测。当训练集出现类别数据不平衡的问题时，可以利用smote算法平衡数据。类别不平衡，即训练集中某类数据样本数量和其他类样本数量差值过大，使得部分机器学习模型失效的问题。实验中Logistic回归算法便不适合处理类别不平衡问题，因为当绝大多数样本都为正常样本而其他类样本很少，Logistic模型倾向于把待预测的大部分样本判定为正常，这样虽然准确率(P)很高，却达不到较高的召回率(R)[17]。因此针对这种问题，需要使用smote算法平衡训练集中的类别数据后再进行预测，才能保证预测结果具有参考性。

基于SVD分解的预测模型可以忽略用户的偏好主题，直接利用用户的点赞行为实现用户特征预测，但缺陷在于运算复杂度较高，假设对矩阵Aa×b做分解，则时间复杂度为O(b2a+ba2)≈O(b3)，而预测新数据集时需要重构矩阵，加大了运算复杂度，因此难以预测新数据集。

2 基于LDA的用户特征预测模型

本文基于用户信息以及其点赞微博文本，建立主题模型，进而预测新用户的特征。首先利用预处理后的用户点赞微博数据训练LDA主题模型、确定合适主题数并划分主题；然后基于“用户—主题”的关联规则建立对应稀疏矩阵，并训练预测模型；最后加入新数据集，得到预测结果。本文提出的基于LDA的用户特征预测模型具体流程如图1所示。

图1 基于LDA主题提取的用户特征预测模型流程图

2.1 LDA主题模型

通过LDA主题模型可以对用户相应的点赞微博文本进行主题划分。LDA模型是一个基于“文档—主题—词”的三层贝叶斯文档主题生成模型,即认为一篇文档中每个词都是通过“某个概率确定主题，并从该主题中概率确定某个词语”过程得到的，文档到主题以及主题到词均服从多项式分布。当利用LDA主题模型获取微博平台上用户点赞微博的主题时，LDA主题模型的文档对应为点赞微博集合，词对应为用户点赞微博文本，LDA根据文档中的词不断训练得出文档的主题以及主题分布，便能得到点赞微博文本-主题概率多项分布。假设D={d1,d2,…,dM}为微博文本集合，M为训练的微博文本数量，每个文本有N个词，n代表主题数，θi为微博di的主题分布，φti,j为主题ti,j的词分布，其中Dirichlet(α)是参数为α的先验分布，是LDA通过训练生成文本对应的主题分布；Dirichlet(β)是参数为β的先验分布，模型中训练生成主题对应的词分布，则模型中各种变量关系可表示为

(5)

其中，式(5)中隐含变量的条件分布可以通过联合概率分布计算为[18]:

(6)

本文以用户的点赞微博文本集合为输入，训练LDA模型，进而获得每条微博的主题分布。

2.2 最佳主题数确定

在构建主题模型前，需要基于“用户—点赞微博”的二元关系，使用Python语言提供的机器学习包Gensim对用户的点赞微博文本进行LDA主题划分，而合适的主题数量n是重要参数。主题数n是由LDA模型根据文本集合划分的主题个数，每一个主题均由词的概率分布组成，主题数过大或者过小均会影响到预测模型的结果。Gensim提供了一个数值定量评估方法“主题相干性”判定主题模型质量的好坏，它表明人们对主题模型的理解更倾向于属于同一主题的单词在语料库中共同出现的频率，该方法得到的数值称为“一致性系数”，可用于评估LDA在不同主题数下的分类效果，取值范围∈[-1.0,1.0]，通常数值越高，该主题数下的主题模型效果越好[19]。常见的一致性系数有CV、CP、CUMass等，其中CV组合了间接余弦度量、标准化点互信息和布尔滑动窗口，综合性能更强[20]，因此本文使用CV的数值度量主题模型输出的一致性。通过对LDA主题的一致性系数计算，可以为用户点赞信息集合提供适当的主题数量，并将每条点赞微博分配到相应主题中。

确定最佳主题数n后便得到“点赞微博—主题”的概率分布，即点赞微博di在每个主题tn下的主题分布概率pin，其中主题集合Topic={t1,t2,…,tn}，微博di的主题分布θi={(t1,pi1),(t2,pi2),…,(tn,pin)}，LDA主题模型完成训练。

2.3 用户—主题稀疏矩阵

选取点赞微博di中最高概率值所对应的主题t，作为该微博所属主题。假设User={user1,user2,…,userm}为用户集合，以主题集合和用户集合分别作行标签与列标签，建立“用户—主题”稀疏矩阵，该稀疏矩阵建立规则为：若用户点赞过主题tj下的微博，记为1；若该用户未点赞过主题tj下的微博，则记为0。因此构建的“用户—主题”稀疏矩阵Cm×n示例如式7所示。将该稀疏矩阵以及用户对应的特征作为输入，训练预测模型。本次实验中选用的预测模型同样是Logistic回归模型。

(7)

2.4 用户特征预测

新数据集加入时，新用户点赞信息的主题分布可由训练好的主题模型推断得到，进而实现新用户的特征预测。清洗数据后，首先将新数据集中用户点赞微博文本集合输入到已训练的LDA主题模型中，实现主题划分；其次仍构建相应的“用户—主题”稀疏矩阵；最后使用已训练Logistic回归模型，预测新数据中用户特征，完成预测。

3 实验结果与分析

3.1 数据描述

微博作为当今人们交流和共享信息的热门平台，能够提供用户行为等各方面丰富的公开数据，为学术研究奠定了充足的数据基础。因此，本文以微博平台数据为例，提取某热点事件下参与讨论的所有用户近1年内的点赞微博，并剔除点赞次数低于5次的用户以及被点赞次数低于10次的微博文本，最终筛选出64 598位用户及这些用户的点赞微博共计1 854 548条，并划分训练集和测试集，分别作为训练模型的数据以及待预测的新数据集。测试集为总数据集中随机选取的约20%用户以及对应的点赞微博。最终得到表1所列数据集合：

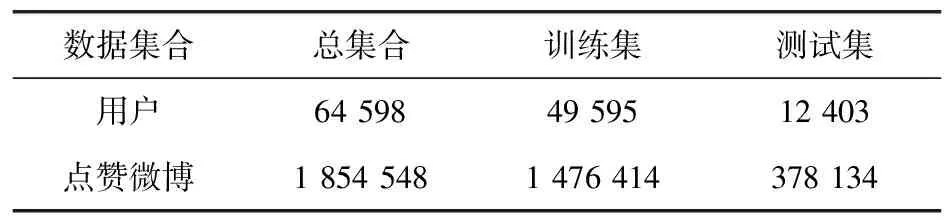
表1 数据清洗后有效用户数以及相应的点赞微博数

待预测特征有性别、认证类型、是否本科学历、年龄阶段。表2为训练集中有特征信息的用户数量分布。

表2 训练集中用户特征分布情况

表2显示训练集中仅性别中男女类别比例相近，而其他特征均出现一个类别远高于另一类别的数据不平衡特点。为保证预测模型预测结果准确，对于类别不平衡的数据需要利用smote算法做类别平衡后再训练预测模型。

3.2 确定合适主题数

一致性系数计算通过Gensim包中的ConherenceModel实现。实验中以10为间隔，可以得到不同主题数对应的一致性系数变化趋势，具体如图2所示。

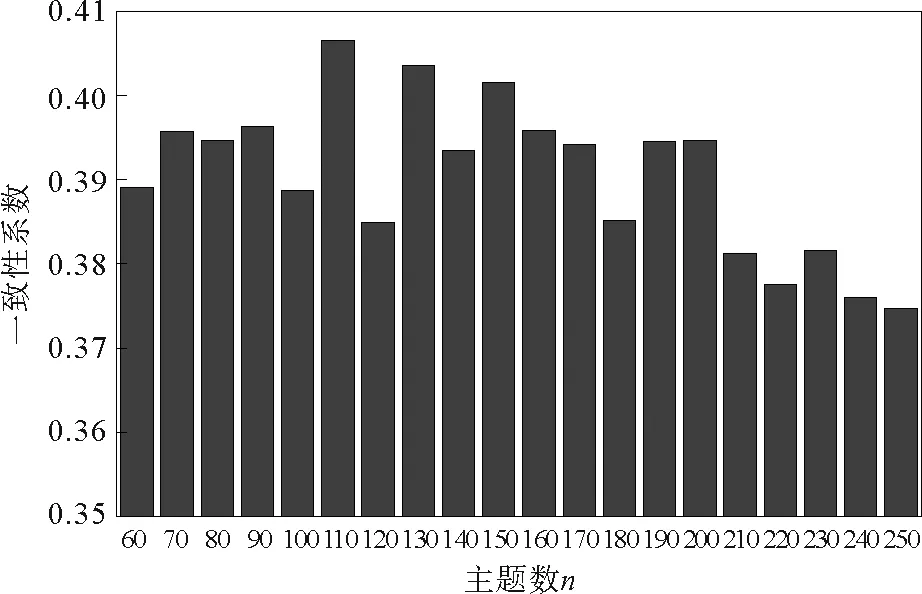
图2 不同主题数下的一致性系数

图2可知当主题数n=110时，一致性系数均高于其他主题数下的相应值，主题模型在该主题数下的表现更佳，因此设置实验中LDA主题模型的主题数n为110。

3.3 评价指标

实验中模型的评价指标主要依据F1值。二分类问题通常将样例以真实的类别和预测后的类别为基础，组合为真正例(True Positive)、假正例(False Positive)、真反例(True Negative)以及假反例(False Negative)4种情形，在该组合基础上可得到学习器评价指标：准确率(Precision)与召回率(Recall)，定义为：

(8)

(9)

通常准确率与召回率呈反比关系。为了能够兼顾准确率和召回率，Pazzani[21]等在同时考虑两者的基础上提出了F-Measure指标。F-Measure指标即F1值，可看作准确率与召回率的一种调和平均。F1取值范围为[0,1]，通常值越高说明预测效果越好，定义为：

(10)

3.4 结果分析

利用Logistic回归模型完成测试集的预测。基于LDA的预测模型(当主题数n=110时)与基于SVD的预测模型(当降维数k=110时)对测试集用户特征预测结果评估具体如图3所示。

图3a表明，两种模型仅预测性别特征时F1值相近，其他特征预测中LDA预测模型F1值均高于SVD预测模型，并在预测本科学历特征时有最明显的差异，差值高达约0.15。进一步比较在测试集中，基于LDA的预测模型与基于SVD的预测模型对用户特征预测运算时间，结果如图3b所示。图3b可见，两种模型预测测试集中各类用户特征时，基于LDA的预测模型运算时间均低于基于SVD的预测模型运算时间，其中在性别预测中时间减少68.19%，本科学历预测中时间减少66.45%，认证类型预测中时间减少74.34%，年龄阶段预测中时间减少67.40%，运算时间平均减少69.09%。

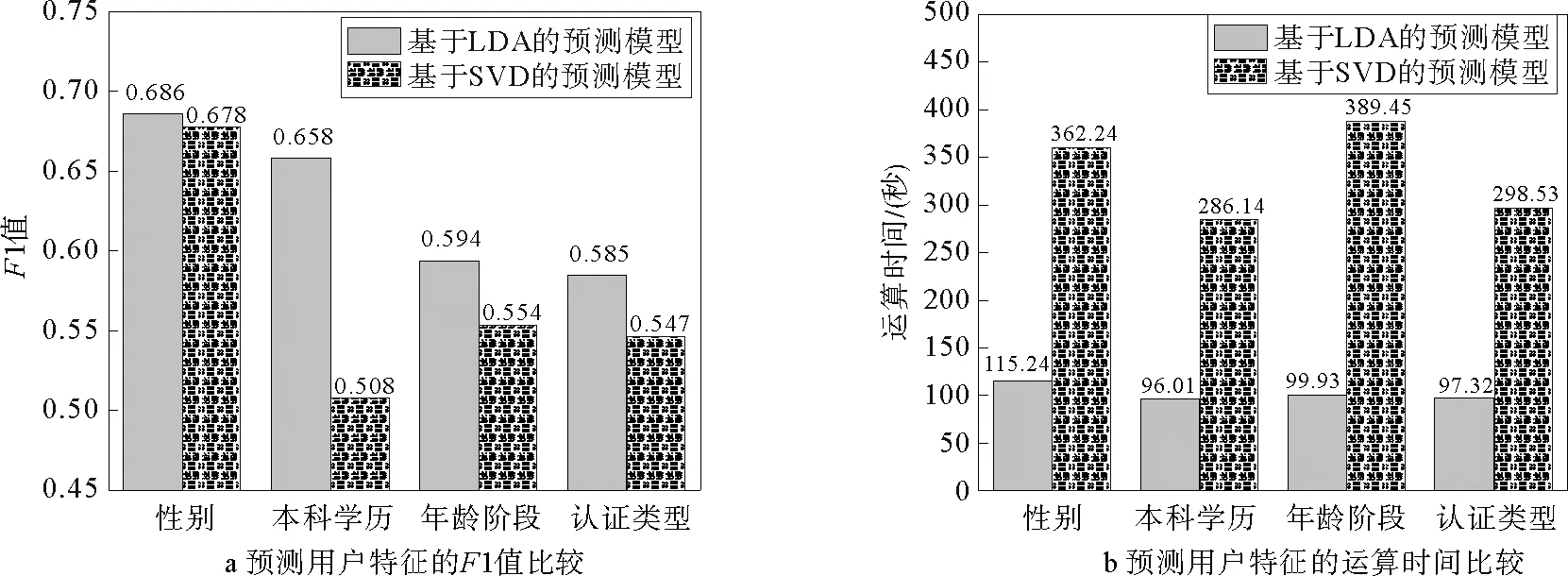
图3 两种预测模型的F1值比较

综合分析，基于LDA的预测模型在F1值以及运算时间均优于基于SVD的预测模型，说明LDA主题模型较SVD模型能够更好的实现对新数据集用户特征的预测。

4 结论

本文的研究基于用户基本特征信息以及用户相应的点赞微博文本数据，对新数据的用户特征进行预测。首先对已有数据集进行数据清洗，筛选出符合条件的用户以及相应的点赞微博文本，利用LDA主题模型划分用户点赞微博文本的主题，并选用“一致性系数”作为确定最佳主题数的指标后，完成LDA主题模型的训练；其次基于“用户-主题”关联规则建立对应的稀疏矩阵，作为训练Logistic预测模型的输入；最后通过加入新数据集，根据已有模型判断新数据集中用户点赞文本的主题分布，从而实现对新数据集用户的特征预测，并将预测结果与传统的SVD方法得到的结果进行比较。实验结果表明，基于LDA的预测模型在预测用户特征时，各特征相应的F1值以及运算时间均优于基于SVD的传统预测模型，并且由于LDA模型在预测新数据集时，仅需根据已训练的LDA主题模型便能够得到新数据集的主题分布，很大程度上降低运算的复杂度，同时也提高了运算速度，相较SVD模型需重构矩阵计算，更具有预测效率。

本文工作中提出的基于LDA的预测模型不仅弥补了现有标签不能有效反映用户真实偏好的缺陷，并且为快速预测在线用户特征提供了另一条便捷途径。本文的研究也存在以下不足：实验数据仅基于微博平台上某个特定事件，存在局限性，若选取多个热点事件下的用户及其点赞信息集合作为训练集，提升训练集的数据质量，在预测新数据的用户特征时是否能够提升预测效果；此外由于用户的每一条点赞微博服从主题的概率分布，若构建用户-点赞微博主题概率分布矩阵而非建立用户-主题稀疏矩阵，以该矩阵训练模型用于预测用户特征，预测结果有何变化。本文中未讨论这些情况，后续可以对该预测模型拓展相关工作，进一步提高模型性能。