COVID-19疫情防控需要社区监测及接触者追踪并重

赵子鸣，勾文沙，高晓惠,2，陈清华,3,4

(1.北京师范大学系统科学学院,北京 100875；2.山西财经大学统计学院,太原 030006；3.新英格兰复杂系统研究所,马萨诸塞州 剑桥 02139；4.布兰迪斯大学化学学院,马萨诸塞州 沃尔瑟姆 02453)

流行病指可以感染众多人口的传染病，能在较短的时间内快速蔓延。自从有文字记载以来，流行病就存在于世，肺结核、疟疾、黑死病、天花、霍乱、艾滋病、流感等流行病都曾经夺取数千万人的生命，给世界经济带来巨大损失，是人类共同的敌人。为了防控流行病，人们投入了大量的精力，虽然部分流行病的治疗和预防工作已经取得突破性进展，但仍旧有新的流行病不断爆发。人们逐渐意识到，病原体随着人类活动在社会关系网络上的传播方式可能是一个重要原因。研究发现，人类的社交关系网络是具有无标度特性的复杂网络，如果不改变网络结构，病原体的传播就不会停止[1-2]。因此，仅凭医学治疗是难以防控疫情的。这就需要群体和个人采取基于网络传播的公共卫生控制方法[3-5]，通过改变网络结构，切断病原体传播途径，减缓疫情的蔓延，为医学治疗赢得更多的时间[6]。

从病原体传播的角度来看，最有效的方法是切断一切传播途径，即将每个人都完全隔离起来，但这对于人类社会来说几乎是不可能的。当前，人们主要采取了两种基于网络传播的干预措施，即接触者追踪[6]和社区监测[7]。接触者追踪是传统的公共卫生控制方法。在追踪接触者的过程中，工作人员会询问已知患者近期的直接接触者，并依照流行病潜伏期时间对这些接触者进行监测或隔离，从而减少病原体的传播途径。Cameron Browne等[8]研究发现接触者追踪在埃博拉疫情防控中发挥着重要作用。世界卫生组织[9]和美国疾病控制与预防中心[10]强调了接触者追踪的重要性，但对于基本再生数为2.5左右的流行病来说，追踪率至少需要达到70%才能有效控制疫情[11]。

然而，接触者追踪高度依赖于患者对自身直接接触者的了解程度，因此，在人口密集，陌生人接触频繁的区域，存在大量无法追踪的隐匿接触者[7]，给疫情防控带来了巨大挑战。为了找到这些无法被及时追踪的密切接触者，可以依托社区对全体居民的健康状况进行监测，一旦发现异常，就迅速隔离患者。社区监测干预措施既包括个人对健康状况的自我检查与主动汇报，也包括社区工作人员的日常监测。Yaneer Bar-Yam等[7]在2016年通过建立基于空间网络的SEIR模型来模拟流行病的传播方式，证明了当依从率达到40%时，社区监测干预措施能迅速将有效再生数降低至1以下。研究表明，武汉的社区监测与出行禁令对COVID-19的疫情防控工作确实有重要影响[12]。韩国、意大利等国家和地区也进行了严格的社区监测，有效遏制了疫情的蔓延。当前，很多国家正在采取这种干预措施来应对疫情的发展。

越来越多的证据表明，COVID-19[13]存在相当比例的无症状感染者[14-16]，这些个体将病原体传播给他人而自身没有表现出任何症状，并且无症状感染者在患者群体中占有相当大的比例[17-19]，这给世界各国的疫情防控工作带来了新的挑战。Sheryl L.Chang等[17]研究发现对于存在无症状感染者COVID-19来说，依从率至少需要达到90%，社区监测干预措施才能在短期内发挥显著作用，然而，这在现代社会中是难以实现的。因此，本文通过基于空间SEIR模型的多主体模拟，证明当存在无症状感染者时，单独实施接触者追踪或者社区监测可操作性都不强，共同实施、二者并重才能控制疫情蔓延。

1 基于SEIR模型建立病原体传播网络

本文基于SEIR模型[20-21]定义个体的健康状态，通过具有周期性边界的有限空间结构种群模型来模拟病原体的传播过程。对于N个可能患病的个体，每个个体可能处于以下4种健康状态之一：易感状态(S)、潜伏状态(E)、传染状态(I)、收治状态(R)。个体按顺序从一个状态转换到另一个状态S→E→I→R。

•S(Susceptible)：易感状态，目前健康，但能够被传染的状态；

•E(Exposed)：潜伏状态，处于已感染、无症状显现状态，本文假设潜伏状态的个体不具有传染性；

•I(Infectious)：传染状态，处于已感染且能够传染易感个体的状态，包括无症状感染者I1和有症状感染者I2；

•R(Removed)：收治状态，包括被治愈个体和死亡个体。

本文进一步通过多主体模拟的方法模拟病原体在网络上的传播过程及干预措施。如图1所示，在病原体传播网络中，一个方格代表一个个体，每个个体处于以下4种状态之一(绿色方格处于S状态，橙色方格处于E状态，红色方格处于I状态，蓝色方格处于R状态)。同时，每个个体与其周围(上下左右)的4个个体有直接连边，我们称其为邻居。在不同的网络中，邻居数记为λ。对于每个I状态的个体，其携带的病原体在网络中可能以概率τ通过近距离传播的方式将病原体传播给自己的邻居，也可能以概率η通过远距离传播的方式将病原体传播给随机选择的一个易感个体。

图1 病原体在网络上的传播方式

在网络中，假设流行病在人群中的传播主要有两种方式，分别是近距离传播方式和远距离传播方式[7]。我们通过以下方式进行模拟。

近距离传播方式：在每一个时间步内，对于每一个处于I状态的个体，个体与其邻居进行一次接触，在接触过程中，每个S状态的邻居都有τ的概率被I状态个体传染，在下一个时间步进入E状态。τ被称为近距离传染率，反映了实际传播过程中，熟人之间因密切接触被传染，传染率较大且只传播邻居节点，常表现为聚集性染病。

远距离传播方式：在每一个时间步内，每个个体都会从群体中任选一个个体进行接触，如果接触的两个个体分别处于I状态和S状态，则S状态个体以概率η被I状态个体传染，在下一个时间步进入E状态。η被称为远距离传染率，反映了实际传播过程中，陌生人之间因偶然性接触被传染，传染率较小，常表现为因旅居公共场所而染病。

2 干预措施的模拟与分析

2.1 社区监测干预措施

在疫情防控工作中，迅速隔离传染源是重要的干预措施，社区监测正是人们迫切需要的。在现代社会中，社区作为人类居住的固定场所，人员密集，活动频繁，是进行疫情防控的重点区域。因此，依托社区来进行疫情监测，具有经济、高效及可操作性强等优点。社区监测既包括政府以社区为基本单位，对社区内居民的健康状况进行排查、统计与监测，对社区居民的行为进行建议、指导与约束的公共卫生政策；同时，也包括居民检查自身的健康状况，并主动向卫生防疫部门报告。

在模拟时，允许病原体自由传播一段时间，并在第T0个时间步时开始社区监测。假设即使在社区监测开始后，I状态个体也并不能被及时隔离，所有I状态个体可以在传染期的第一个时间步内自由传染他人。本文设置监测率α以模拟现实中因为各种原因(如监管不力、个体拒绝配合等)造成的不完整检测，在传染期的第二个时间步时，对于每个处于I状态个体，都以概率α被隔离，被隔离的个体不能再传染他人。如果I状态个体在第二个时间步没有被隔离，则其在第二个时间步内可以自由传染他人，但会在传染期Γ的下一个时间步内继续被监测，同样以概率α被隔离，直到I状态个体在经历传染期Γ天后转换到R状态。

κ≈1-(1-α)(Γ-1)

(1)

对于传染期Γ，监测率α，我们可以计算因社区监测被隔离的I状态个体比例κ，它度量了社区监测的预期干预效果。我们称κ为社区监测的依从率，表示在所有的I状态个体中，部分个体(以依从率κ选择)在传染期Γ内的某一时间步被隔离，其余个体在整个传染期Γ内都有能力传染他人。

如图2所示，当传染期Γ≈8天时，依据式1)可以得到监测率随依从率的变化曲线。可以看出，监测率α会随着依从率κ的提升而超线性增长，即提升相同的依从率κ所需要的增加的社区监测力度越来越大，提升难度越来越高。一般认为，严格的社区监测干预措施的依从率κ可以达到60%，此时需要每天发现12.27%左右的I状态个体，而非常不严格的社区监测的依从率κ仅在10%左右，群体中每天只有1.49%的I状态个体主动报告病情。因此，本文假设依从率κ≈10%是现代人类社会群体中的自然水平，总有少部分人会自觉检查自身的健康状况，并主动向卫生防疫部门报告。

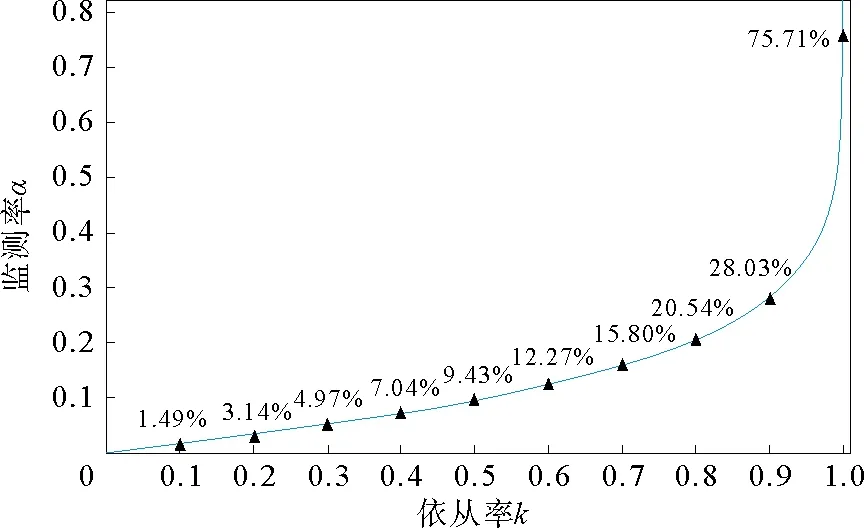
图2 社区监测难度的超线性增长

需要特别说明的是，在I状态个体中，可能存在一定比例ρ的无症状感染者。其中，无症状感染者，指无相关临床症状(如发热、咳嗽、咽痛等)，但呼吸道等标本核酸检测或抗体检测呈阳性且具有流行病传播风险的个体。由于无任何症状显现，难以通过社区监测将其查出并隔离，因此，这部分I状态个体在整个传染期Γ都有能力传染他人，造成社区监测干预措施的部分失效。因此，需要更多干预措施来辅助社区监测，共同防控疫情。

2.2 接触者追踪干预措施

除了进行社区监测外，人们还可以询问被隔离患者的活动轨迹，统计患者的密切接触者名单，工作人员依据名单追踪接触者并对其进行病原体检测。这样的干预措施即为接触者追踪。对于密切接触者，由于防疫部门会对其全部进行隔离观察及病原体检测，因此不管患者是否会显现症状，都可能在潜伏期或传染期内被追踪并隔离，隔离之后不会再传染他人。

为简化模拟过程，我们只追踪因社区监测而被新隔离的个体在前一个时间步的接触者(包括邻居和远程接触者)，既不考虑之前时间步的接触者，也不对接触者中的病例进行接触者追踪。此外，由于人口的快速流动及公共场合隐匿接触的存在，追踪到所有的被传染者是有一定难度的。因此，如果被追踪的个体已经被感染(可能处于E状态或者I状态)，则会以概率θ被隔离，否则可以继续在网络中接触其他个体，θ被称为追踪率。

2.3 模拟参数的确定

本文模拟了一个种群规模N为10 000(100×100),且具有周期性边界的四邻居规则网络。在模拟中,我们将一个时间步设定为1天进行多主体模拟。首先，个体会可能会处于以下4种状态(S、E、I、R)，且每个个体都有(上下左右)4个邻居，即λ=4。模拟开始前，随机初始化选择0.02%的个体处于E状态，且处于潜伏期的第一天；0.02%的个体处于I状态，均为有症状传染者且处于传染期的第一天。对于新产生的I状态个体以ρ的概率为无症状感染者，其余为有症状传染者，我们分别以ρ≈30%[18]和ρ≈60%[19]进行多主体模拟。

本文依据发生在中国武汉地区的新冠肺炎病例数据来调整模拟参数(近距离传染率τ和远距离传染率η)，使得模拟的情况与COVID-19的真实情况一致。研究表明[22]，中国武汉地区的新冠肺炎潜伏期Δ≈6天(平均值)，传染期Γ≈8天(平均值)。为了更好地模拟在中国武汉COVID-19的真实情况，根据近期的研究结果[9,23-25]，设定参数近距离传染率τ≈0.096，远距离传染率η≈0.008，此时基本再生数R0≈2.20。本文通过比较新增病例数、累计病例数及有效再生数Rt随时间t的变化来展示两种干预措施的效果。对于每一组参数，都进行1 000次模拟，然后计算平均值。其中，基本再生数R0，表示在疫情爆发初期(即t=0时刻)，假设所有接触到的个体均处于S状态，刚进入I状态的个体在传染期Γ天内传染的平均人数。有效再生数Rt，表示在时刻t，被感染(刚进入E状态)的个体预期传染的平均人数。对于Rt，存在一个明确的阈值：当Rt>1时，新增病例数会持续增长；当Rt<1时，新增病例会迅速减少，证明疫情得到了有效控制。

3 干预措施的效果与讨论

3.1 ρ=0情况

图3a、图3b、图3c展示了当不存在无症状感染者(ρ=0)时，社区监测干预措施对于新增病例数、累计病例数和有效再生数Rt的影响，干预措施从疫情爆发的第70天开始(T0=70天，不同颜色的曲线表示不同的依从率κ)。研究发现，如果不进行社区监测，在疫情爆发后4个多月内，有效再生数都稳定在1.25左右，累计病例数呈指数型增长，迅速导致群体中20%左右个体患病，后果不堪设想。然而，从第70天开始进行社区监测后，如果有60%的个体能够积极配合卫生防疫部门的工作(κ≈60%)，有效再生数Rt就可以迅速下降至1以下，新增病例数由增加转为减少，疫情发展迅速迎来拐点，社区监测干预措施效果显著。我们的模拟结果与相关文献的研究成果基本一致[7]。

图3d、图3e、图3f展示了当不存在无症状感染者(ρ=0)时，接触者追踪干预措施对有效再生数Rt的影响，干预措施从疫情爆发的第70天开始(T0=70天，不同颜色的曲线表示不同的追踪率θ)。本文假设依从率κ≈10%是现代人类社会群体中的自然水平，总有少部分人会自觉检查自身的健康状况，并主动向卫生防疫部门报告。因此，图3d反映的是仅实施接触者追踪干预措施的效果。研究发现，由于接触者追踪依赖于被隔离的病例，如果仅通过追踪被隔离传染者的密切接触者来防控疫情，效果并不显著。然而，如图3e及图3f所示，随着社区监测干预强度的提升(依从率κ≈40%)，接触者追踪的作用被逐渐放大。当追踪率θ=40%时，仅需要依从率κ≈40%即可达到图3c中依从率κ≈60%的疫情干预效果。研究表明，接触者追踪的作用一定程度上依赖于社区监测的干预力度。

图3 干预措施效果(不存在无症状感染者ρ=0)

3.2 ρ≈30%情况

当I状态群体中出现30%的无症状感染者时，由于这部分I状态个体自身不会表现出任何症状，因此社区监测措施对其失效。那么，如果在一定力度的社区监测基础上，对被隔离的传染者进行询问统计，追踪其密切接触者并检测隔离，能否应对无症状感染者的出现给疫情防控工作带来的挑战呢？图4展示了社区监测和接触者追踪干预措施对有效再生数Rt的影响，干预措施从疫情爆发的第70天开始(T0=70天，不同颜色的曲线表示不同的追踪率θ)。在图4a中，当依从率κ≈40%时，80%左右的追踪率θ可以将有效再生数Rt降低至1以下，对比图3c可以看出无症状感染者对疫情防控工作带来的挑战以及接触者追踪干预措施的显著效果。在图4b中，当依从率κ≈60%时，40%左右的追踪率θ可以将有效再生数Rt降低至1以下；在图4c中，当依从率κ≈80%时，不需要接触者追踪就可以将有效再生数Rt降低至1以下。然而，在实际中，不论是依从率，还是追踪率，达到80%的水平都是难以实现的，因此，当I状态群体中出现30%的无症状感染者时，控制社区监测力度使得依从率κ≈60%，控制接触者追踪的力度使得追踪率θ=40%是最有效的θ≈40%。研究证明了当存在无症状感染者时，社区监测和接触者追踪干预措施共同实施的必要性和干预效果的显著性。

图4 干预措施效果(ρ≈30%)

3.3 ρ≈60%情况

当I状态群体中出现更多的无症状感染者(ρ≈60%)时，图5展示了社区监测和接触者追踪干预措施对有效再生数Rt的影响，干预措施从疫情爆发的第70天开始(T0=70天，不同颜色的曲线表示不同的追踪率θ)。在图5a中，当依从率κ≈40%时，即使追踪率θ再高也无法将有效再生数Rt降低至1以下；在图5b中，当依从率κ≈60%时，100%左右的追踪率θ可以将有效再生数Rt降低至1以下；在图5c中，当依从率κ≈80%时，80%左右的追踪率θ可以将有效再生数Rt降低至1以下。然而，在实际中，不论是依从率，还是追踪率，达到100%的水平都是无法做到的[26]，因此，当I状态群体中出现60%的无症状感染者时，控制社区监测力度使得依从率κ≈80%，控制接触者追踪力度使得追踪率θ=80%是唯一且最为有效的。研究表明，当无症状感染者较多时，如果社区监测干预力度不足，再精准的接触者追踪也无法取得显著的效果，社区监测和接触者追踪二者共同干预是非常必要的。

图5 干预措施效果(ρ≈60%)

3.4 网络结构的鲁棒性分析

本文进一步分析了不同网络结构中干预措施的效果。如图6所示，对于不同的无症状感染者比例ρ，我们分别模拟了病原体在3种不同网络结构中的传播过程。干预措施从疫情爆发的第70天开始(T0=70天)，红色、橙色、黄色曲线分别表示病原体在四邻居规则网络、八邻居规则网络及Kleinberg小世界网络中有效再生数Rt随时间的变化的情况。其中，Kleinberg小世界网络考虑了节点间的异质性，特别是幂律分布的连接情况，与人类社会网络更加相似[1]。Kleinberg网络允许个体拥有不同数量的远程邻居，并且对于任意两个个体来说他们成为远程邻居的概率随着距离的增大而减小。在模拟中，Kleinberg网络中的每个个体在4个直接邻居的基础上，还会以一定概率随机产生远程邻居，远程邻居产生的概率为两个体的曼哈顿距离平方的倒数。

图6 不同网络结构下干预措施效果

此外，在不同网络结构的模拟中，近距离传染率τ和远距离传染率η有所调整，以使得模拟与COVID-19的真实情况一致。研究表明，无论哪种网络结构，相同的干预措施都可以有效控制疫情的蔓延，干预措施对于不同的网络结构是具有高度鲁棒性的。

4 结语

基于SEIR模型，本文在空间上建立了具有周期性边界的病原体传播网络，并通过多主体模拟的方法来模拟COVID-19的实际传播情况。首先，我们通过定义近距离传染率τ和远距离传染率η来模拟病原体在网络中的传播过程。其次，我们通过控制依从率κ和追踪率θ来量化社区监测和接触者追踪的干预力度。进一步，我们依据相关研究来确定武汉地区COVID-19的潜伏期Δ≈6天，传染期Γ≈8天，基本再生数R0≈2.20，以模拟COVID-19的实际传播情况。最后，我们针对不同的无症状感染者比例ρ分别进行多主体模拟。研究表明，当I状态群体中出现30%的无症状感染者时，控制社区监测力度使得依从率κ≈60%，控制接触者追踪的力度使得追踪率θ=40%的干预效果与依从率κ≈80%时的单独实施社区监测的效果相似，但前者更具可行性。当I状态群体中出现60%的无症状感染者时，控制社区监测力度使得依从率κ≈80%，控制接触者追踪的力度使得追踪率θ=80%是唯一且有效的干预方法。研究证明了存在无症状感染者的情况下，社区监测和接触者追踪干预措施共同实施的必要性、可行性和干预效果的显著性。此外，我们的研究结论对于不同的无症状感染者比例ρ及不同的网络结构都具有高度鲁棒性。

本文研究认为，为了较好地控制传染病的蔓延，依从率和追踪率都需要达到一定的程度。依从率取决于个体和群体在有症状情况下的及时汇报，与一个国家和地区的政策执行力度和个人遵守程度有关，在政府和各种群体组织的积极干预和协助下，可以通过广泛宣传等手段提高个人认识，从而提高依从率。同时，随着调查手段的发展与信息技术的进步，接触者追踪的广度和准确率都有了极大提升，例如基于移动通讯定位技术的APP可以使得寻找接触者更加迅捷[6]，使得从确诊患者出发更精准地追踪其密切接触者，也可以促进社会大众更及时地了解自己有无密切接触风险。本研究可以更加科学地解释中国在COVID-19防治工作中的成功，对于世界各国的疫情防治工作具有一定的指导意义。

感谢狄增如教授和李小萌博士的讨论与建议。