区间值模糊图的若干运算及相关性质

华毛加，索南仁欠

(1.青海师范大学 数学与统计学院,青海 西宁 810008；2.青海师范大学 研究生院，青海 西宁 810008)

0 引言

1975年Zaded[1]提出了区间值模糊集的概念，它是模糊集的一种推广形式.区间值模糊集对于不确定的现象比传统的模糊集更具描述，因此，区间值模糊集得到了广泛的研究和应用，比如模糊控制、医疗诊断、多值逻辑、智能控制等方面，区间值模糊集起到了很重要的作用.区间值模糊集理论应用到图论上，就有了区间值模糊图理论.区间值模糊图是由Chen与Horng[2]提出的，推广了模糊图.随后许多学者对区间值模糊图做了细致的研究，如Akram与Dudek[3]定义了区间值模糊图的笛卡尔积、合成、并、联运算，讨论了一些性质，并给出了区间值模糊完全图的定义，分析自补和弱自补区间值模糊完全图的一些性质；Talebi与Rushmanlou[4]研究了区间值模糊图同构的一些性质；杨文华[5]定义了区间值模糊图的直接乘积、半强乘积、强乘积以及字典乘积.本文将定义区间值模糊图的若干运算，并研究其相关的性质，进一步补充和完善区间值模糊图理论.

1 预备知识

设I={[a,b]|0≤a≤b≤1}(即[0,1]中所有闭区间构成的集合),I中的序关系定义为：[a1,b1]≤[a2,b2]⟺a1≤a2且b1≤b2,∀[a1,b1],[a2,b2]∈I.

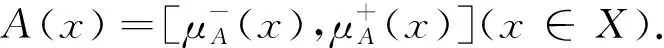
2)对于任意的集合V，在V×V-{(x,x)|x∈V}上定义等价关系～如下：

(x1,y1)～[x2,y2]⟺(x1,y1)=(x2,y2)或者x1=y2,x2=y1.

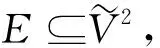
定义1.2[7]设A和B为X上的两个区间值模糊集，则对于x∈X:

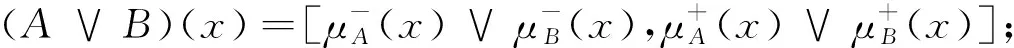
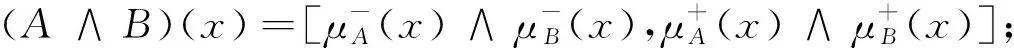
③(A∨B)∧A=A;

④(A∧B)∨A=A;

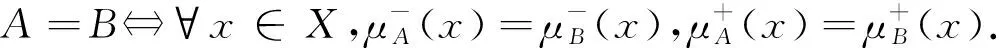
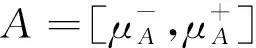
则称序对G=(A,B)是图G*=(V,E)的区间值模糊图,记图G*上的所有区间值模糊图的集合为(G).

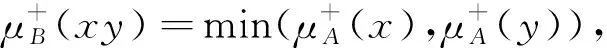
2)若X的两个区间值模糊集μ和v满足μ(x)≤v(x)(∀x∈X),则记μ≤v.若两个区间值模糊图G=(A,B)和H=(A1,B1)满足A1≤A,B1≤B,则称H是G的偏区间值模糊子图.

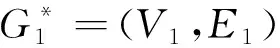
①映射f∶V1→V2称为从G1到G2的同态，若f满足下面的条件：

②映射f∶V1→V2称为从G1到G2的弱同构，若f是双射且满足下面的条件：

i)f是G1到G2的同态.

③映射f∶V1→V2称为从G1到G2的同构，若f是双射且满足下面的条件：

2 主要结果

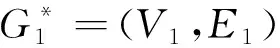
E={(x1,z)(y1,z)|z∈V2,x1y1∈E1}∪{(x1,x2)(y1,y2)|x1y1∈E1，x2y2∈E2},并且

((x1,x2)∈V1×V2),

(x1y1)∈E1,z∈V2),

(x1y1∈E1,x2y2∈E2).

注：G1⊗G2≠G2⊗G1，易知通过弱乘积运算得出的新图G1⊗G2=(A，B)依然是一个区间值模糊图.

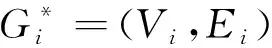
证明由弱乘积的定义可知

(∀(x1,x2)∈V1×V2),

(∀(x1,x2)∈V1×V2),

(∀(x1,z)(y1,z)∈E),

(∀(x1,z)(y1,z)∈E),

(∀(x1,x2)(y1,y2)∈E),

(∀(x1,x2)(y1,y2)∈E).

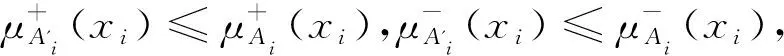
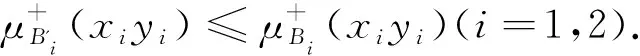
即μA＇(x1,x2)≤μA(x1,x2),同理可证

μB＇((x1,z)(y1,z))≤μB((x1,z)(y1,z)),(∀(x1,z)(y1,z)∈E),

μB＇((x1,x2)(y1,y2))≤μB((x1,x2)(y1,y2)),(∀(x1,x2)(y1,y2)∈E).

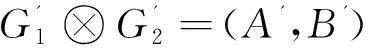
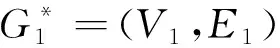
E={(x,x2)(x,y2)|x∈V1,x2y2∈E2}∪{(x1,z)(y1,z)|z∈V2,x1y1∈E1}

∪{(x1,x2)(y1,y2)|x1y1∈E1,x2y2∈E2}∪{(x1,x2)(y1,y2)|x1y1∉E1,x2y2∈E2},

并且

((x1,x2)∈V1×V2),

(x∈V1,x2y2∈E2),

(x1y1∈E1,z∈V2),

(x1y1∈E1,x2y2∈E2),

(x1y1∉E1,x2y2∈E2),

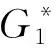
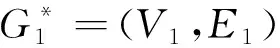
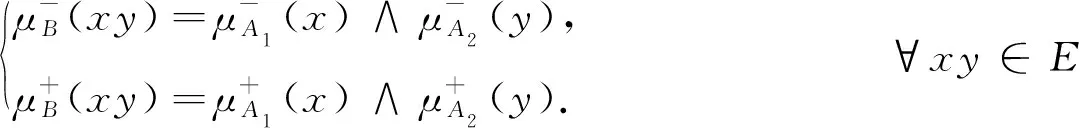
注：G1-G2=G2-G1,可发现G1-G2=(A，B)是一个二部区间值模糊图,所以事实上这个运算是一个构造二部区间值模糊图的过程.

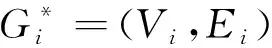
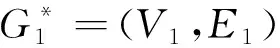
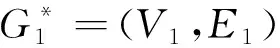
E={(x,x2)(x,y2)|x∈V1,x2y2∈E2}∪{(x1,z)(y1,z)|z∈V2,x1y1∈E1}

∪{(x1,x2)(y1,x2)|x1y1∈E1,x2y2∈E2}∪{(x1,x2)(y1,y2)|x1y1∉E1,x2y2∉E2},

并且(i),(ii),(iii),(iv)与定义2.3相同.

注：G1*G2≠G2*G1,易知G1*G2=(A，B)也是区间值模糊图.

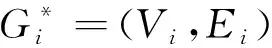
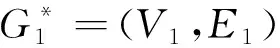
E={(x,x2)(x,y2)|x∈V1,x2y2∈E2}∪{(x1,z)(y1,z)|z∈V2,x1y1∈E1}

∪{(x1,x2)(y1,y2)|x2y2∈E2,x1,y1∈V1且x1≠y1},并且

((x1,x2)∈V1×V2),

(x∈V1,x2y2∈E2),

(x1y1∈E1,z∈V2),

注：G1∘G2≠G2∘G1，易发现G1∘G2=(A，B)也是区间值模糊图.

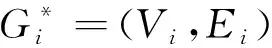
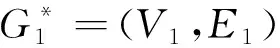
证明由G1⊗G2的定义可知,对于任意的z∈V2，x1y1∈E1,

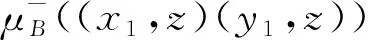
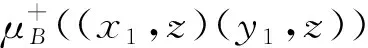
同理，对于任意的x1y1∈E1,x2y2∈E2,有

因此,G1⊗G2=(A,B)是强区间值模糊图.

类似地，可以证明下面的定理.

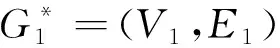
定理2.14设G=(A,B)是区间值模糊图G1=(A1,B1)和G2=(A2,B2)的弱乘积，G＇=(A＇,B＇)是区间值模糊图G3=(A3,B3)和G4=(A4,B4)的弱乘积，G1≅G3,G2≅G4，则G≅G＇.

证明由于G1≅G3且G2≅G4,所以存在两个映射,分别是f1∶V1→V3和f2∶V2→V4,且满足

定义f∶V1×V2→V3×V4，其中f(x1,x2)=(f1(x1),f2(x2))(∀(x1,x2)∈V1×V2) ，这里将f((x1,x2))简写成f(x1,x2),不难验证f是同构的.

类似地，其余的运算也有这样的性质.