交换环上的绝对w-E-纯模

2022-08-03李庆

云南大学学报（自然科学版） 2022年4期

李庆

(西南民族大学数学学院，四川成都 610041)

1 预备知识

本文恒设R为具有单位元的交换环.R-模正合列是纯正合列[1]，是指对任意R-模N，0 →A⊗RN→B⊗RN→C⊗RN→0仍保持正合.这种情况下，称f(A)是B的纯子模.如果R-模M是任意包含它的R-模的纯子模，就称R-模M为绝对纯R-模.注意绝对纯模也就是文献[2]中所谓的FP-内射模.由此，关于模上的纯性的研究得到了广泛关注[3-6].文献[7]将绝对纯模进行了推广，提出了E-纯正合列和绝对E-纯模等概念.所谓R-模正合列是E-纯正合列[7]，是指对任意内射R-模N，0 →A⊗RN→B⊗RN→C⊗RN→0仍保持正合.这种情况下，称f(A)是B的E-纯子模.如果R-模M是任意包含它的R-模的 E-纯子模，就称R-模M为绝对E-纯模.随着Glaz 等[8]引入半v模(semi-divisorial modules)，也就是王芳贵等[9]在整环上定义的w-模.随后，文献[2]将w-模推广到任意的交换环上研究，产生了交换环上的w-算子和w-模.w-算子和w-模的引入将乘法理想理论与同调理论逐步结合起来，产生了许多漂亮的结果[10-17].邢世奇和王芳贵等在文献[10-11]中将w-算子引入到纯性理论的研究中，提出了w-纯正合列和w-纯子模以及绝对w-纯模的概念.R-模w-正合列0 →A→B→C→0称为w-纯正合列[10]，是指对任意R-模N，诱导的同态序列0 →A⊗RN→B⊗RN→C⊗RN→0是w-正合列.特别，若A为B的R-子模，R-模同态序列0 →A→B→B/A→0是w-纯正合列，称A为B的w-纯子模.如果A是所有包含它的R-模的w-纯子模，则称A为绝对w-纯子模[11].易知R-模A是绝对w-纯子模当且仅当对任意正合列0 →A→B→C→0都是w-纯正合列.本文主要在上述文献的启发下结合w-算子进一步推广纯性的相关研究，提出了w-E-纯正合列和w-E-纯子模以及绝对w-E-纯模.

下面回顾一些常用定义和结果.假设J是交换环R的理想，由文献[18]，J称为GV-理想，是指J是R的有限生成理想，且自然同态φ:R→HomR(J,R)是同构的.GV(R)代表R中所有GV-理想.设R-模M，记torGV(M)={x∈M|Jx=0对某J∈GV(R)}.若torGV(M)=M，称M为GV-挠模；若torGV(M)=0，称M为GV-无挠模.GV-无挠R-模M称为w-模，是指对任意J∈GV(R)有设f:M→N是R-模同态，若对R-的任意极大w-理想m，fm:Mm→Nm是单同态(满同态或同构)，则f称为w-单同态(w-满同态或w-同构).R-模同态序列A→B→C称为w-正合列，是指对R的任意极大w-理想m诱导的Rm-模同态序列Am→Bm→Cm是正合列.由文献[19]命题1.1 知，R-模同态序列是w-正合列当且仅当f:A→B是w-单同态当且仅当ker(f)是GV-挠模；R-模同态序列是w-正合列当且仅当g:B→C是w-满同态当且仅当cok(g)=C/Im(g)是GV-挠模.由文献[20]定理2.7 知，R-模M是GV-挠模当且仅当对R的任意极大w-理想m，Mm=0.本文用A≤B表示A是B的子模，E(A)表示A的内射包.若没特别声明，设R-模M,N，我们将M⊗RN简记为M⊗N.本文涉及的其他概念等，参见文献[21].

2 绝对w-E-纯模

定义1R-模短正合列称为w-E-纯正合列，是指对任意作为R-内射w-模 E，其诱导的序列0 →E⊗A→E⊗B→E⊗C→0是w-正合列.这里的单同态f:A→B称为w-E-纯单同态，f(A)称为B的w-E-纯子模.如果R-模A作为任意一个R-模的子模都是w-E-纯子模，我们就称A为绝对w-E-纯模.R-模正合列称为w-E-纯正合列，是指是w-E-纯正合列，也就是f:A→B是w-E-纯单同态.

由定义1 知，R-模A是绝对w-E-纯模当且仅当任意正合列0 →A→B→C→0都是w-E-纯正合的.

命题1设R为任意交换环，A,B,C,D是R-模.

(1)若f:A→B和g:B→C都是w-E-纯单同态，则g f:A→C也是w-E-纯单同态.

(2)设单同态f:A→B和态射g:B→C使得g f:A→C是w-E-纯单同态，则f:A→B是w-E-纯单同态.特别，当A≤B≤C，A是C的w-E-纯子模，则A也是B的w-E-纯子模.

(3)设A≤B≤C，A是C的w-E-纯子模，B/A是C/A的w-E-纯子模，则B是C的w-E-纯子模.

(4)设A≤B≤C，B是C的w-E-纯子模，则B/A是C/A的w-E-纯子模.

(5)设交换图为

(a)如果该交换图是推出图，f是w-E-纯单同态，g是满同态，则 α是w-E-纯单同态；

(b)如果该交换图是拉回图，α是w-E-纯单同态，β是满同态，且ker(β)是B的w-E-纯子模，则f是w-E-纯单同态.

(3)由(2)可知，A是B的w-E-纯子模.下面考虑以下行列都是正合的列的交换图：

任取内射w-模E，由A是B的w-E-纯子模，A是C的w-E-纯子模，且B/A也是C/A的w-E-纯子模，于是我们有以下行列都是w-正合的交换图：

由文献[21]引理6.3.6 得E⊗B→E⊗C是w-单同态.因此，B是C的w-E-纯子模.

(4) 考虑以下行列都是正合列的交换图：

任取内射w-模E，由B是C的w-E-纯子模，于是有以下行为w-正合且列为正合列的交换图：

由文献[21]引理6.3.6 得E⊗B/A→E⊗C/A是单同态，于是B/A是C/A的w-E-纯子模.

(5) (a)假设已知条件中的交换图是推出图，于是有下列行列都是正合列的交换图：

任取内射w-模E.因f是w-E-纯单同态，故有下列行为w-正合列且列为正合列的交换图：

由文献[21]引理6.3.6 得E⊗C→E⊗D是w-单同态，故 α是w-E-纯单同态.

(b)假设已知条件中的交换图是拉回图，于是有下列行列都是正合列的交换图：

因α是w-E-纯单同态且ker(β)是B的w-E-纯子模，从而对任意内射w-模E有以下行列为w-正合列的交换图：

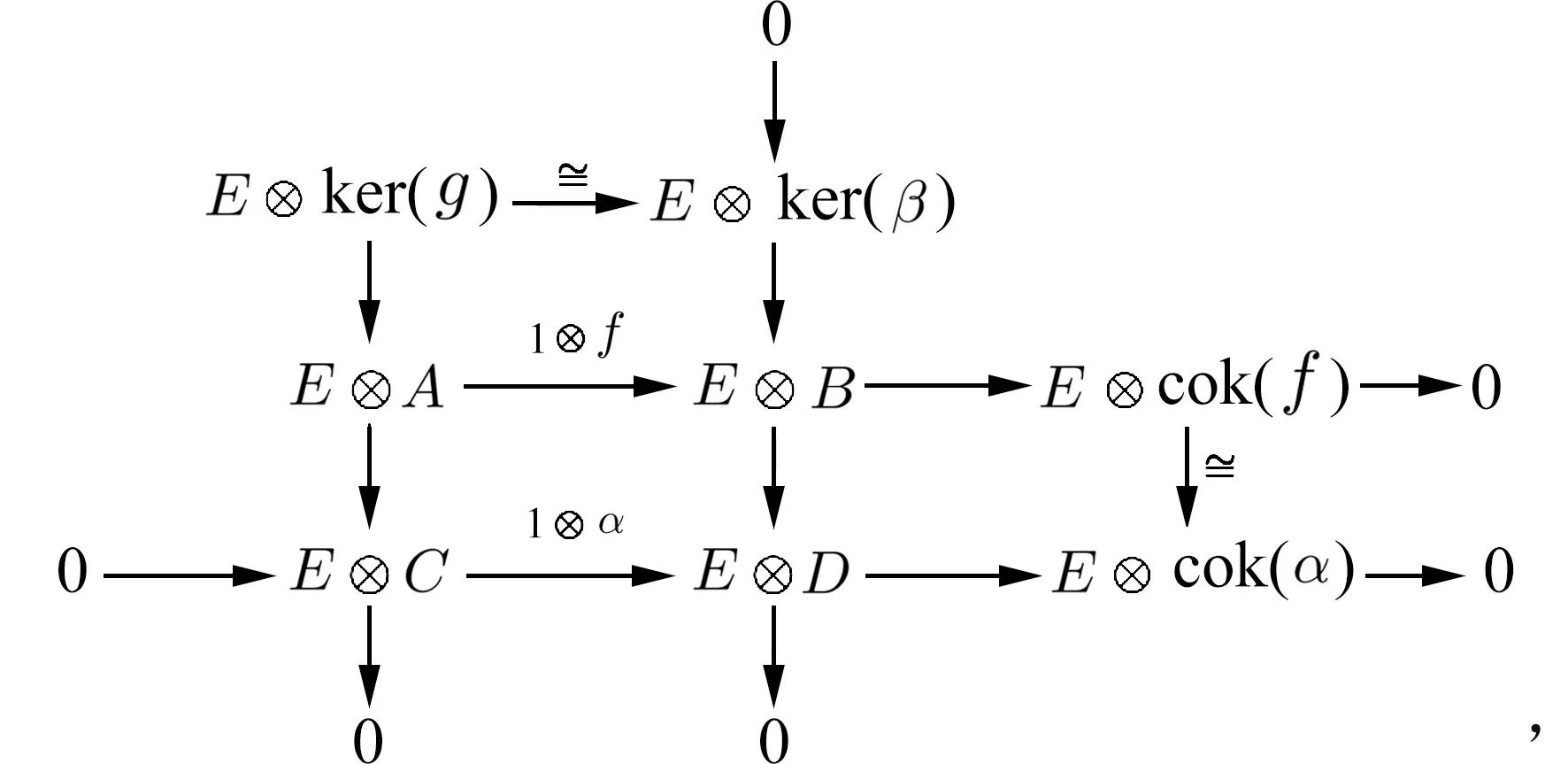
于是对R的任意极大w-理想m，有下列行列都正合的交换图：

由蛇形引理，ker((1⊗f)m)≅ker((1⊗α)m).因α:C→D是w-E-纯单同态，故1⊗α:E⊗C→E⊗D是w-单同态，从而(1⊗α)m:(E⊗C)m→(E⊗D)m是单同态.因此ker((1⊗α)m)=0，故ker((1⊗f)m)=0，从而(1⊗f)m:(E⊗A)m→(E⊗B)m是单同态，故1⊗f:E⊗A→E⊗B是w-单同态.因此，f:A→B是w-E-纯单同态.证毕.

定理1设M是绝对w-E-纯模，且K≤M，则K是绝对w-E-纯R-模当且仅当K是M的w-E-纯子模.

证明“⇒” 由绝对w-E-纯R-模的定义直接可得.

“⇐”设K′是包含K的任意R-模，考虑K→M与K→K′的推出图，我们有以下行正合的交换图：

由M是绝对w-E-纯R-模，且K是M的w-E-纯子模，于是对任意内射w-模E，有以下行列均为w-正合的交换图：

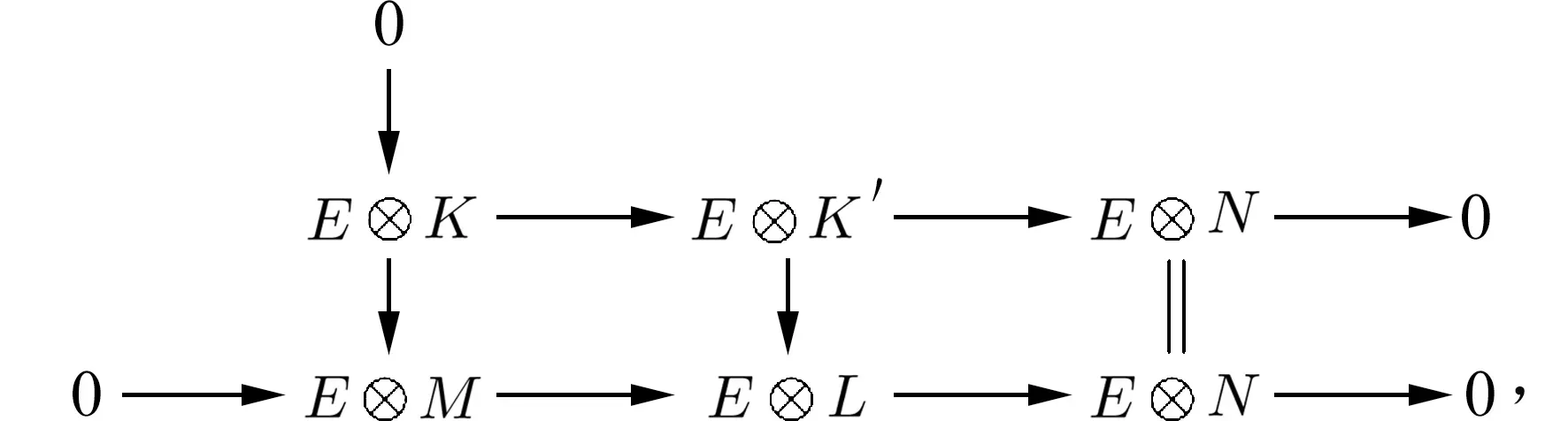
于是E⊗K→E⊗K′是w-单同态，从而K→K′是w-E-纯单同态.因此，K是绝对w-E-纯R-模.证毕.

定理1 说明绝对w-E-纯模类在w-E-纯子模下是封闭的.

定理2设R-模正合列0 →A→B→C→0，其中A,C都是绝对w-E-纯模，则B也是绝对w-E-纯模.

证明任取包含B的R-模D，考虑B→D与B→C的推出图，我们有以下行列正合的交换图：

因A,C都是绝对w-E-纯模，故对任意内射w-模E 有以下行列是w-正合的交换图：

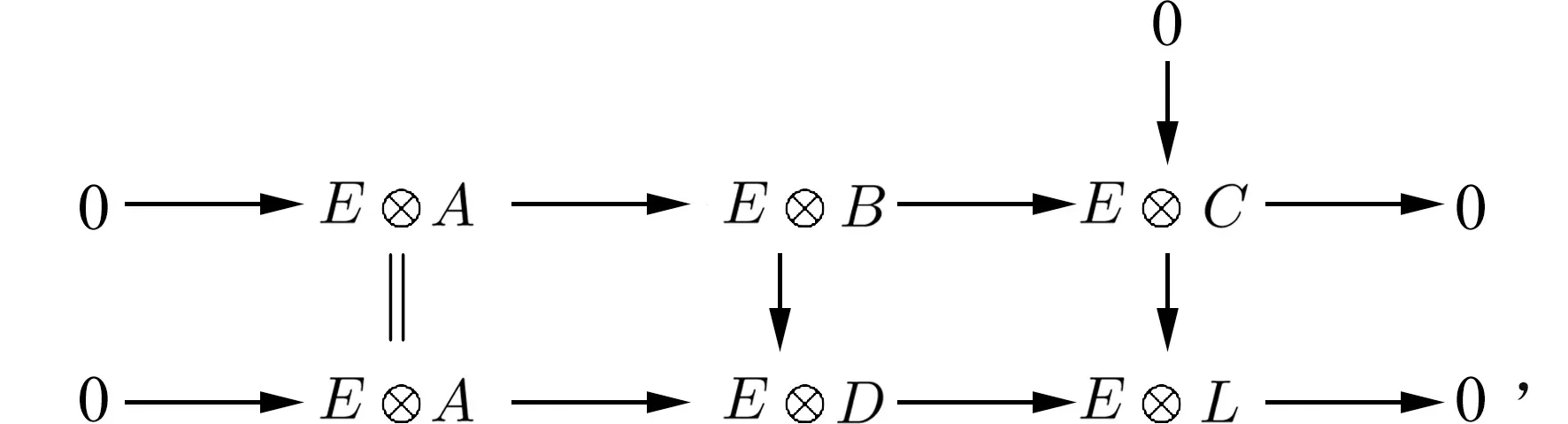
由文献[21]引理6.3.6，E⊗B→E⊗D是w-单同态.故B→D是w-E-纯单同态.因此，B是绝对w-E-纯模.证毕.

定理2 说明绝对w-E-纯模类在其扩张之下是封闭的.

推论1设A≤B，且均为R-模，若B和E(B)/A都是绝对w-E-纯模，则B/A也是绝对w-E-纯模.

证明由A≤B≤E(B)，因B是绝对w-E-纯模，于是B就是E(B)的w-E-纯子模.由命题1(4)，B/A是E(B)/A的w-E-纯子模.又因E(B)/A是绝对w-E-纯模，故由定理1，B/A是绝对w-E-纯模.证毕.

定理3设R为交换环，以下各条等价：

(1)A是绝对w-E-纯R-模；

(2)A是任意包含它的内射模的w-E-纯子模；

(3)A是其内射包E(A)的w-E-纯子模.

证明(1)⇒(2)⇒(3)由绝对w-E-纯模的定义，显然成立.

(3)⇒(1)任取包含A的R-模B，因E(A)内射，故有交换图

故g f=h是单同态.因A是E(A)的w-E-纯子模，也就是说h:A→E(A)是w-E-纯单同态.故g f是w-E-纯单同态.由命题1(4)，f:A→B是w-E-纯单同态.因此，A是绝对w-E-纯R-模.证毕.

下面我们讨论环R上的任意R-模都是绝对w-E-纯模的情况.回顾文献[13]，R称为w-IF环，是指R上每个内射w-模都是w-平坦模.R-模M称为w-平坦模[15]，是指对任意R模w-单同态f:A→B，其诱导的序列1⊗f:M⊗RA→M⊗RB也是w-单同态.R-模M称为w-余纯平坦模[12]，是指对R-上任意内射w-模，tor(E,M)是GV-挠模.

定理4设C是R-模，则任意R-模正合列0 →A→B→C→0是w-E-纯正合列当且仅当C是w-余纯平坦模.

证明“⇒” 不妨取正合列0 →K→P→C→0，其中P为投射R-模.任取内射w-模E，于是有正合列

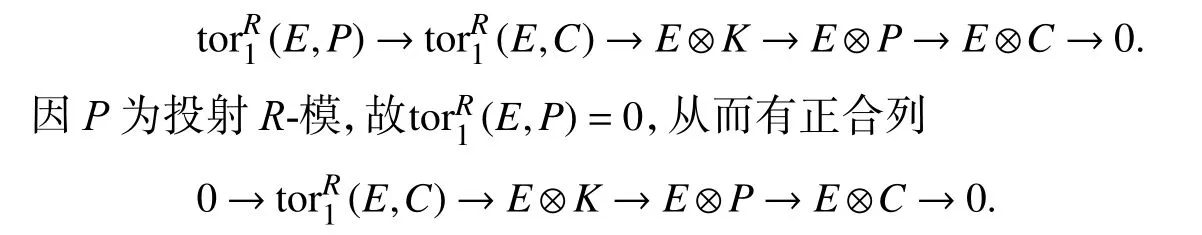
由已知条件可知0 →K→P→C→0是w-E-纯正合列，故序列

是w-正合的.因此，是GV-挠的.故C是w-余纯平坦模.

“⇐”假设C是w-余纯平坦模，于是对任意内射w-模E，是GV-挠的.对R的任意w-理想m，任取正合列R-模0 →A→B→C→0，于是有正合列从而有正合列

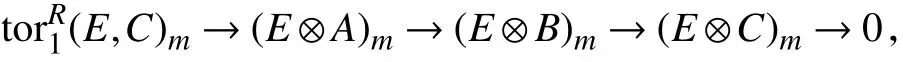
故对R的任意w-理想m，0 →(E⊗A)m→(E⊗B)m→(E⊗C)m→0是正合列.故0 →E⊗A→E⊗B→E⊗C→0是w-正合列.因此，0 →A→B→C→0是w-E-纯正合列.证毕.

从定理4 可以看出，在某种程度上绝对w-E-纯模可看成是w-余纯平坦模的对偶.回顾文献[14]，设R是交换环，n是非负整数，设R-模M，若对任意R-模N，是GV-挠模，则称M的w-平坦维数小于等于n，记为w-fdR(M)≤n.我们知道M是w-平坦模当且仅当w-fdR(M)=0当且仅当对任意R-模N，是GV-挠模.类似文献[7]定理2.18，我们得出以下结论.

定理5设R为任意交换环，下列各条等价：

(1)每个R-模都是绝对w-E-纯模；

(2)R是w-IF环；

(3)每个R-模都是w-余纯平坦模；

(4)对任意R-模M，E(M)/M是w-余纯平坦模.

证明(2)⇒(3)参见文献[13]定理6.5.

(1)⇒(2)若R不是w-IF环，则存在有一个内射w-模E不是w-平坦模，于是w-fdR(E)≥1.从而存在R-模A使得不是GV-挠模.取正合列0 →A′→P→A→0，其中P为投射R-模.我们得到如下正合列

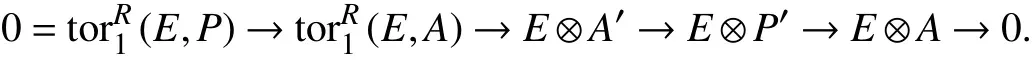
因每个R-模都是绝对w-E-纯模，故A′是绝对w-E-纯模，从而0 →E⊗A′→E⊗P′→E⊗A→0是w-正合列.故是GV-挠模，矛盾.因此，R是w-IF环 .

(3)⇒(4)显然成立.

(4)⇒(1)设任意R-模M，E(M)/M是w-余纯平坦模.由定理4，0 →M→E(M)→E(M)/M→0是w-E-纯正合列.故M是E(M)的w-E-纯子模.由定理3，M是绝对w-E-纯模.即每个R-模都是绝对w-E-纯模.证毕.

最后，我们类似于模的纯内射性和纯平坦性的讨论，思考相对于w-E-纯正合列下模的内射性和平坦性间题.

定义2(1)R-模M称为w-E-纯内射模，是指M相对于任意的R-模的w-E-纯正合列保持其内射性.即对任意的w-E-纯正合列0→A→B→C→0，诱导的同态序列0 →HomR(C,M)→HomR(B,M)→HomR(A,M)→0是正合列.

(2)R-模M称为w-E-纯平坦模，是指M相对于任意的R-模的w-E-纯正合列保持其平坦性.即对任意的w-E-纯正合列0 →A→B→C→0，诱导的同态序列0 →M⊗RA→M⊗RB→M⊗RC→0是正合列.

引理1R-模M是w-E-纯平坦模当且仅当M的特征模M+(=HomZ(M,Q/Z))是w-E-纯内射模.

证明设任意的w-E-纯正合列0 →A→B→C→0.R-模M是w-E-纯平坦模当且仅当0 →M⊗RA→M⊗RB→M⊗RC→0正合当且仅当0→(M⊗RC)+→(M⊗RB)+→(M⊗RA)+→0正合当且仅当0 →HomR(C,M+)→HomR(B,M+)→HomR(A,M+)→0正合当且仅当M+是w-E-纯内射模.其中倒数第2 个充分必要条件的成立是因为(N⊗RM)+≅HomR(M,N+).证毕.

由定义，我们知道纯正合列是E-纯正合列，E-纯正合列是w-E-纯正合列，反过来会有什么结果呢?我们给出下面结论.

命题2设R为任意交换环，以下各条件等价：

(1)任意w-E-纯正合列都是纯正合列；

(2)任意R-模M都是w-E-纯平坦模；

(3)对任意R-模M，M+是w-E-纯内射模.

证明(1)⇒(2)设任意R-模M，任取w-E-纯正合列0 →A→B→C→0.由已知条件可知0 →A→B→C→0是纯正合列，故其诱导R-模序列0 →M⊗RA→M⊗RB→M⊗RC→0是正合列.因此，M是w-E-纯平坦模.

(2)⇔(3)由引理1 直接可得.

(2)⇒(1)任取w-E-纯正合列0 →A→B→C→0，任取R-模M，因M是w-E-纯平坦模，故0 →M⊗RA→M⊗RB→M⊗RC→0是正合列.因此，0 →A→B→C→0是纯正合列.证毕.

命题3设R为任意交换环，则以下各条件等价：

(1)任意w-E-纯正合列都是E-纯正合列；

(2)任意内射R-模M都是w-E-纯平坦模；

(3)对任意内射R-模M，M+是w-E-纯内射模.