竖直弯管水合物浆液流动模拟研究
2020-12-17杨蕊刘德俊王鹤超
杨蕊 刘德俊 王鹤超


摘 要: 以竖直倾斜弯管内流动的天然气水合物浆液作为研究对象,运用Fluent软件进行数值模拟,并通过FBRM实验进行验证。主要研究了天然气水合物浆液在管道内流动、水合物颗粒体积分数的变化导致水合物颗粒不断聚集情况,因此研究了不同流速、不同管径对天然气水合物颗粒体积分数产生的影响,并对其影响稳定流动的情况进行分析。研究结果表明:低流速下,受到浮力的影响,水合物颗粒会在进入弯管前的直管段处在管道上方聚集,在弯管处体积分数达到峰值;管径不变的情况下,流速越低,弯管处水合物体积分数越大,聚集范围也越大;流速不变情况下,管径越大,水合物体积分数在整个流动过程中变化越剧烈,弯管处水合物体积分数越大,聚集的风险越高;模拟的结果与实验的误差约为11%。模拟结果能够对水合物浆液输送提供理论支持。
关 键 词:水合物浆;数值模拟;颗粒体积分数;竖直弯管
中图分类号:TQ 022.4 文献标识码: A 文章编号: 1671-0460(2020)11-2597-05
Simulation Study of Hydrate Slurry Flow in Vertical Bend
YANG Rui 1, LIU De-jun 1, WANG He-chao 2
(1. School of Petroleum and Natural Gas Engineering, Liaoning Shihua University, Fushun 113001, China;
2. China Petroleum Pipeline Engineering Co., Ltd. Southeast Asia Project Department, Langfang 065000, China)
Abstract: Taking natural gas hydrate slurry flowing in a vertically inclined elbow as a research object, numerical simulation was performed by using Fluent software, and simulation results were verified by FBRM experiments. The natural gas hydrate slurry flowing in the pipeline was mainly studied as well as the hydrate particles continuous accumulation caused by the change of the volume fraction of hydrate particles. Therefore, the effect of different flow rates and different pipe diameters on the volume fraction of natural gas hydrates was studied. The effect of the volume fraction of natural gas hydrates on the steady flow was also analyzed. The research results showed that: at low flow rates, under the effect of buoyancy, hydrate particles accumulated above the pipe at the straight pipe section before entering the bend, and the volume fraction peaked at the bend; When the pipe diameter was constant, the lower the flow rate, the larger the hydrate volume fraction at the bend, and the larger the range of aggregation; Under the same flow rate, the larger the pipe diameter, the more drastic the hydrate volume fraction change in the flow process, the larger the hydrate volume fraction at the bend, the higher the risk of aggregation; The error between the simulation result and the experiment result was about 11%. The simulation results can provide theoretical support for hydrate slurry transportation.
Key words: Hydrate slurry; Numerical simulation; Volume fraction of particles; Vertical elbow
天然气水合物是由甲烷为主的烃类气体和水构成的晶体化合物,由于其高度浓缩的特性非常适用于天然氣的运输和储存[1]。我国的南海海域天然气水合物资源丰富,具有较高的开发价值,因此研究水合物浆液管道流动特性是实现深海开发利用天然气水合物资源的重要环节,是实现管输技术大规模工业应用的重要基础[2-5]。对于纯水体系的水合物浆液在管道中的流动特性国内外专家学者进行了广泛的研究。王武昌[6]等进行了水合物颗粒体积分数为0~65.2%的四氢呋喃水合物浆液流动实验,提出临界水合物体积分数,在临界以下为牛顿流体,超过临界时,压降梯度随体积分数的增加急剧增加,浆体为Bingham流体。JOSHI[7]通过循环管路中水合物形成实验,提出纯水系统管道中天然气水合物堵塞的机理,将天然气水合物形成分为3个区域,以1区到2区即均相到非均相时天然气水合物浓度作为水合物堵塞的指标,而这一指标是由压力、温度、速度方向决定的。DING[8]等同样根据水合物浓度并考虑了水合物颗粒的直径,由此提出了定量估算水合物团聚度和沉积度的几种方法以保障水合物浆液流动稳定。
由此可见,水合物的体积分数是决定水合物浆液安全流动的重要参数。这在Ahmad和李玉星[9-10]等进行的试验中也有所运用。考虑到在深海开发天然气水合物浆液输送过程中,竖直弯管系统是传输中常见结构,因而在本文中探讨水合物浆液在管道内的流动时水合物体积分数变化以及管径、入口流速对竖直弯管内水合物颗粒最大体积分数的影响。
1 模型建立
1.1 几何模型建立
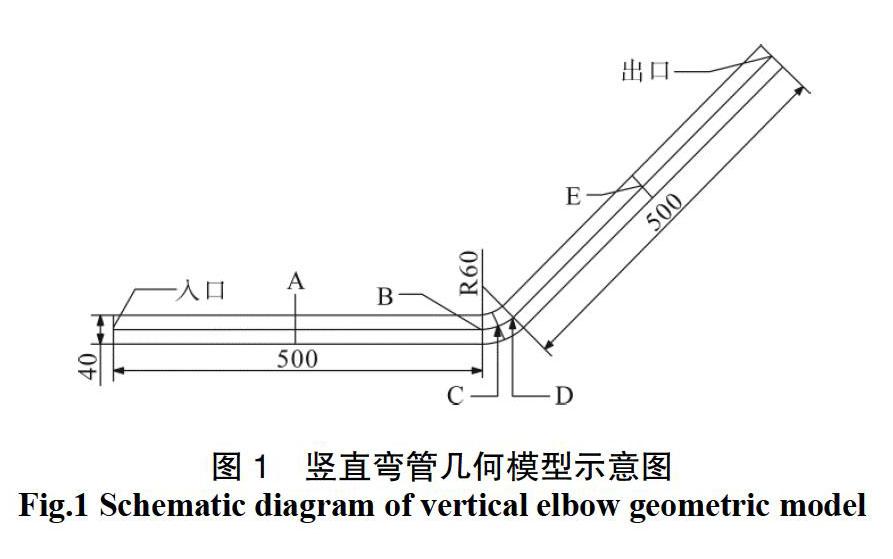
如图1所示, 选取直径40 mm,弯径比R/D=1.5,倾角135°的竖直弯管,前后各取500 mm以克服弯管端面效应。
1.2 数学模型建立
基于颗粒动力学理论的欧拉双流体模型,采用Fluent软件建立模拟水合物浆液在竖直弯管内流动的数值模拟,假设流动过程无相变并且相间无质量和热量传递,水合物颗粒为均匀球体,选用RNG k-ε湍流模型,选取gidaspow模型为相间耦合的曳力模型[11-14]。
1.2.1 基本控制方程
在假设流体具有不可压缩性的前提下,将连续性方程与N-S方程均化后,得到控制方程:
。 (1)
。(2)
式(1)与式(2)中: xi(i =1,2,3)与xj(j =1,2,3)代表坐标分量;ui(i =1,2,3)与uj(j =1,2,3)代表时均速度分量;p代表时均压力 ;μ代表动力黏度 ;ρ代表流体密度 ; 为雷诺应力分量。
1.2.2 湍流基本方程
相比于标准的k-ε模型,重整化群RNG k-ε模型在ε方程中加了一个条件,提高了湍流漩涡方面的精度。这就使RNG k-ε模型可以更好地处理中等强度的旋流和低雷诺数流动。其基本表达形式为:
。(3)
。(4)
在(3)式和(4)式中,k为湍动能, m2·s-3;μ1为紊流黏度,Pa·s;G为湍动能耗散相,G=μ1(▽μ1+(▽μ1)T) ▽μ1;σk为k方程的湍流普朗特数,σk=1.0;σ?为?方程的湍流普朗特数,σ_?=K^2/([C_1-C_(2 )]√(C_μ )) ;C1=1.42;C2=1.68。
1.2.3 相间耦合
CFD模拟中液固相间的耦合作用是通过相间动量交换来实现的,选取gidaspow模型为相间耦合的曳力模型,符合水合物浆液的液固两相间曳力作用,其基本表达式如下:
; (5)
; (6)
。 (7)
在(5)、(6)和(7)中,β為固液传热系数;Res为水合物颗粒雷诺数;CD为曳力系数,与雷诺数相关;ds代表水合物颗粒平均粒径,m。
2 模型验证
2.1 实验验证
Joshi的实验中,水合物体积分数在达到7%时由均相向非均相过渡,因此设置入口水合物体积分数7%,超出这一数值有水合物沉积风险。为了验证模拟可行性,如图2所示,利用自主搭建的实验平台,对管道中水合物颗粒直径与颗粒数进行测定,实验平台主要包括两部分:第一部分由直径为 40 mm,长度为3 000 mm的(4)PVC管路连接水槽与阀门,中间连接如图2的实验管段;第二部分由梅特勒-托利多提供的(8)聚焦光束反射测量仪(FBRM-D600L)测量系统以及型号为 QSF10-10-0.55的潜水泵(2)和型号为PS-61005的普斯变频电源组成的环路系统。测量系统主要用于对管内处于不同流动速度下的水合物颗粒的直径及数量分布进行测量,测量位置分别为直管和倾管中点处(实验管段对应处钻取直径为18 mm的圆形孔洞)。具体的实验流程是首先在水槽(3)中加入代替水合物晶体的冰粒子和去离子水,使冰粒子体积分数达到7%,之后将探头插入测量位置的孔洞中,之后启动潜水泵电源开关,打开实验程序开始测量。测量时间为30 min,数据记录间隔为10 s。
由于启动潜水泵后冰浆开始流动,测得粒子数不断增加,之后粒子数不断下降是因为循环流动的冰粒子被泵叶轮切割,粒径不断减小,10 min后趋于稳定,因此数据从10 min之后开始记录,得到不同直径粒子数分布图(图3)。实验结果发现A点较E点水合物体积分数稍高,这与模拟所得数值情况相同。实验重复测量5次,由粒子数n与粒径d计算该处水合物体积分数φ,与相同条件下模拟所的数值进行比较(图4),实验所得φ值较模拟值高,是由于镜头探入管道的部分导致截面变小。
2.2 管道截面处云图分析
为了更好地研究水合物浆液在管道流动时体积分数的变化,在与粒径分布实验相同的流速、入口体积分数条件下进行了数值模拟,首先得到了如图5所示的直径40 mm管道在流速0.55 m·s-1时A到E截面水合物体积分数云图。水合物浆在流入直管段后,A截面显示水合物颗粒向管道上方聚集,到弯道入口B截面时聚集更明显,这是由于水合物颗粒密度比水低的性质导致在流动的过程中受到浮力的影响不断向管道上方聚集。在进入弯管结构后,涡流降低了聚集的效果,但是弯管结构导致聚集范围集中,这是由于水合物浆液进入弯管后,弯管外侧压力减小,速度升高,颗粒体受到马格努斯力和压力梯度力的影响向高压低速方向聚集[15],在弯道出口D截面水合物颗粒小范围聚集更加明显。进入倾管段后,管壁处没有明显聚集效果,水合物颗粒在管道轴线附近轻微聚集。
3 水合物颗粒体积分数影响因素分析
水合物浆液在流入竖直弯管后发生明显的聚集现象,经过一段时间后可能会有堵塞现象发生,为了水合物浆液的稳定安全流动,研究了0.5、1、 2 m·s-1不同流速,25、32、40 mm不同管径下管道内水合物颗粒体积分数变化,水合物浆液在流入弯管和流出弯管进入倾管段过后表现完全不同,在弯管处水合物体积分数增长最明显,因此着重讨论弯管处水合物颗粒的聚集情况。
3.1 流速对水合物体积分数的影响
水合物浆液流入弯管后沿弯管外侧流体流速增大,压强减小,导致内测水合物聚集,水合物体积分数增大,根据水合物浆液流动云图可知体积分数在轴向变化更加明显,选取B、D截面不同流速下轴向水合物体积分数变化进行比较。管径不变条件下,流速越低,弯管入口处体积分数变化越明显,水合物聚集处体积分数越高;弯管出口处水合物聚集处不仅体积分数高,聚集的范围也更小,即与高流速比较水合物聚集更集中。
3.2 管径对水合物体积分数的影响
由于水合物聚集的方位都在管道顶部,因此对于不同管径对水合物体积分数的影响,根据模拟结果以管道顶部轴向水合物体积分数变化作为参考依据,图6显示在流速1 m·s-1时不同管径下水合物体积分数发生明显变化,主要分为以下几点:
①相同流速下管径越大水合物体积分数变化越剧烈;②直管段位置,管径越大水合物颗粒受浮力影响越明显,水合物颗粒会更早地在管道上部聚集;③竖直弯管位置,管径越大水合物体积分数最大值越大,水合物聚集风险越高,同时进出弯管水合物体积分数变化剧烈,参考2.2分析在此处浆体发生的绕流更加剧烈。见图7。
4 结 论
根据Joshi的实验以7%为水合物颗粒向聚集发展的临界值,超过这一数值的纯水系水合物浆液会在水合物颗粒不断聚集生长的情况下有堵塞的风险,因此在实际输送过程中应避免天然气水合物体积分数超过临界值,保障水合物浆液的稳定流动。经过实验和模拟的研究,发现竖直弯管系统中,水合物颗粒直径范围为10~300 μm,根据粒径分布发现大部分粒径值为50 μm。水合物浆液流入管道后,水合物颗粒会在进入弯管后开始聚集,在流出弯管时达到最大值,在倾斜管道处只在中部轻微聚集。由于弯管处压强差和流速差影响,水合物颗粒聚集明显,因此整个系统中此处的堵塞风险更高。之后通过对3种不同流速、不同管径的弯管体系进行数值模拟,结果表明:
1)在管道直径一定时,不同流速的水合物浆液流入弯管后在弯管上方聚集,流速越低,上方的水合物体积分数越大。随后的聚集范围逐渐增大,流速越低,聚集的范围也越大,因此在水合物浆液输送过程中尽可能提高流速防止发生堵管。
2)在流速一定时,管道直径越大进入弯管前受到浮力影响越大,入口上方体积分数初始值越大,小管径几乎不受浮力影响,这导致管径越大弯管处聚集越强烈,在之后的倾管段也发生急剧的上升,发生堵塞的可能性更高。
3)为了降低管道内水合物聚集、堵塞的风险,在实际情况中通常泵速固定的情况下尽量选择小管径的管道,同时也要考虑水合物颗粒对管道的冲蚀,在弯管处会产生较大的风险,随着水合物体积分数的增加,水合物浆液的黏度也会不断增加向非牛顿流体转化,因此会加剧堵塞的形成。
参考文献:
[1]祝有海,吴必豪,刘玉山.天然气水合物:21世纪的新能源[M].北京:海洋出版社,2017.
[2]闫柯乐,邹兵,姜素霞,等. 水合物浆液流动与流变特性研究进展[J]. 化工进展,2015(7):1817-1825.
[3]朱超,王武昌,王琳.天然气水合物浆流变性的研究现状及发展趋势[J].天然气工业,2011,31(7):77-81.
[4]李长俊,黄婷,贾文龙. 深水天然气水合物及其管道输送技术[J]. 科学通报,2016,61(22):2449-2462.
[5]王武昌,李玉星,樊栓狮,等. 四氢呋喃水合物浆流动特性[J]. 化工进展,2010,29(8):1418-1422.
[6]张威,韩册,吴迪,班久庆,等.天然气水合物的生成机理与防治研究[J].当代化工,2016,45(8):1953-1954.
[7]JOSHI S V, GRASSO G A, LAFOND P G, et al. Experimental flowloop investigations of gas hydrate formation in high water cut systems [J]. Chemical Engineering Science, 2013(97):198-209.
[8]DING L, SHI B H, LV X F, et al.Hydrate formation and plugging mechanisms in different gas-liquid flow patterns [J]. Industrial & Engineering Chemistry Research, 2017, 14 (56): 4173-4184.
[9]MAJID A A A. An investigation on the viscosity and transportability of methane hydrate slurries using a high pressure rheometer and flowloop [D]. Colorado School of Mines,2015.
[10]李玉星,朱超,王武昌,等. 天然氣水合物浆液稳定性影响因素的正交实验[J]. 油气储运,2011,30(9):685-689.
[11]魏丁,王武昌,李玉星,等. 管道CCl3水合物浆流动特性的数值模拟[J]. 油气储运,2016,35(8):828-832.
[12]韦雪蕾,刘宝玉,潘振,等. 水平管道水合物浆液流动特性的数值模拟[J]. 化学工程,2018,46(3):41-46.
[13]江国业,王晓娅.水平弯管内水合物浆的流动特性[J].科技导报,2015,33(2):64-68.
[14]孙贤,刘德俊,王文武,等.弯管体系内浆液流动分析[J].化学工程,2019,47(6):58-63.
[15]郭烈锦.两相与多相流动力学[M].西安:西安交通大学出版社,2001.
