基于改进人工势场法的USV全局路径规划*
2020-12-17薛学华徐海祥龚铭凡
薛学华 冯 辉* 徐海祥 龚铭凡
(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)
0 引 言
水面无人艇(USV)以其无人化水平高、机动性能良好,以及可自主执行任务等优点被广泛应用于军民领域.路径规划是无人艇自主航行模块的核心内容,为满足无人艇在复杂海洋环境下实现自主航行的需求,需要不断提升无人艇的路径规划能力,确保所规划出的路径可靠高效.无人艇路径规划技术是指给定起始点、目标点,以及障碍物信息,在满足一定的评价指标的情况下,在出发点到目标点之间通过使用某种路径规划方法规划出一条最优的安全路径.目前常用的路径规划方法有人工势场法[1]、可视图法[2]、蚁群算法[3]以及遗传算法[4]等.人工势场法是一种虚拟力场法,因其原理简单,运算时间短,生成的路径较为平滑被广泛的应用在无人艇路径规划中[5].可视图法是一种图搜索算法,其优点是结构简洁,规划路径短,缺点是在环境信息复杂的情况下,运算时间会大大增加[6].
传统的人工势场法虽然原理清晰简单但是仍存在以下几个不足之处:狭窄航道内抖振的问题、较为容易陷入局部极小值的问题及目标点不可到达的问题.针对以上缺点,许多学者提出不同的改进方法:刘义等[7]针对局部极小值的问题提出修改斥力势场函数的方法,Saeid等[8]针对目标不能到达的现象提出一种沿墙运动的方法,潘洲等[9]通过设置动态虚假目标点来使机器人离开局部极小值点.
文中针对上述存在的三个不足之处进行详细分析,分别提出三种改进方法:①通过添加艏向角限制,保证船舶狭窄航道内迅速从抖振状态恢复至沿航道方向前进;②提出自适应参数调整回溯法,使得船舶在陷入局部极小值时能够进行回溯并且迅速脱离局部极小值点;③设置人工势场法—可视图法切换策略,使算法能够高效的解决传统方法某些情况下无法到达目标点的问题.
1 人工势场法基本原理
人工势场法最早是由Khatib[10]提出并且将其运用在移动机器人的路径规划领域中,其主体思想是由目标点产生引力场,障碍物产生斥力场,机器人在引力及斥力一起作用下不断向目标点前进.
总势场由引力势场和斥力势场共同叠加组成:
U=Uatt+Urep
(1)
引力势场函数为
Uatt(X)=0.5kρ2(X,Xg)
(2)
斥力势场函数为
(3)
式中:X=(x,y)为机器人位置向量;k,m分别为引力参数与斥力参数;X,Xg,X0分别为机器人当前坐标、目标点坐标以及障碍物坐标;ρ(X,X0),ρ(X,Xg)分别为当前位置到障碍物与当前位置到目标点的距离;ρ0为障碍物影响范围.
通过对势场函数进行负梯度求解,可以分别求出引力与斥力的表达式.
(4)
Frep(X)=-Urep(X)=
(5)
在USV的路径规划过程中,可以通过将障碍物按照船舶尺寸进行膨胀,得到扩展障碍物范围,然后把船舶视为质点的方法进行路径规划,船舶受力见图1.

图1 船舶受力示意图
合力F将驱动船舶规避障碍物,向目标方向运动.该方法虽然原理简单,但仍存在下列几个缺陷.
1) 狭窄航道抖振现象 由于船舶的前进方向完全由引力与斥力的合力决定,当船舶航行至狭窄航道时,合力的方向有可能产生剧烈变化,导致船舶在狭窄航道内出现剧烈抖振的现象.
2) 局部极小值问题 当船舶航行至某一时刻时,若出现船舶的合力为零或者引力与斥力共线,船舶将停止或在局部范围内徘徊.
3) 目标点不可达现象 由式(4)可知,当船舶逐步靠近目标点时,引力会逐渐变小;由式(5)可知,当船舶逐渐接近障碍物的时候,斥力将逐渐增大.因此,当目标点周围存在障碍物时,随着船舶接近目标点,将会出现船舶在目标点周围的局部范围内往复运动的状况,从而导致规划失败.
2 改进人工势场法
2.1 解决狭窄航道抖振问题
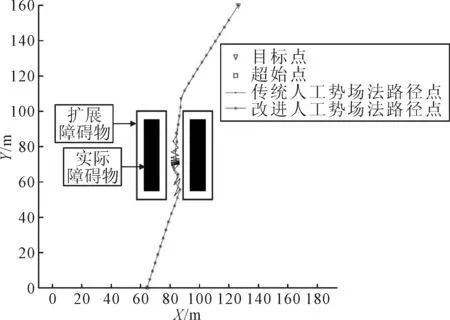
使用传统人工势场法进行路径规划时,在船舶运行至狭窄航道时,会出现不必要的往复抖振现象.主要原因为船舶在狭窄航道时,其主要受力来自目标点的引力以及来自岸壁两边的斥力,当船舶靠近一侧岸壁时,近端岸壁将产生较大斥力将其向远端岸壁排斥,由于航道狭窄,导致船舶在接下来的较小周期内运行到另一个岸壁附近,使得另一岸壁同样产生较大斥力,如此往复,就会导致船舶出现抖振现场,船舶将耗费大量时间才能驶离狭窄航道甚至出现停滞不前的现象,见图2.

图2 人工势场法狭窄航道抖振示意图
针对传统人工势场法出现的抖振现象,分析其主要原因是船舶在接近一侧岸壁时受到斥力作用,以较大角度向反方向运动,使得船舶主要是在垂直岸壁方向运动,而沿着岸壁方向的运动非常少.
为了限制船舶在狭窄航道中垂直岸壁方向的运动,同时使规划出的路径能满足船舶行驶时的实际应用,本文将船舶最大艏向角限制加入到路径规划中,对规划中船舶的方向变化加以限制,从而抑制船舶在接近岸壁一侧的大角度反向运动,达到消除抖振的效果.艏向角限制示意图见图3,其中最大转向角θ=60°,黑色路径点为未添加艏向角时船舶可能出现的大角度反向运动,加粗路径点为添加艏向角限制后,船舶通过设置最大转向角约束避免大角度反向运动现象的产生.
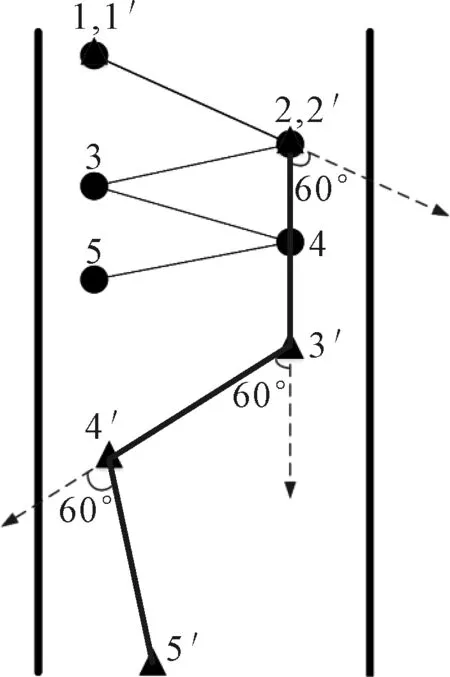
图3 狭窄航道添加艏向角限制示意图
2.2 解决局部极小值问题
局部极小值问题是指船舶在移动过程中的某个时刻,在当前位置下目船舶受到的引力与斥力大小相等,方向相反,导致当前位置点船舶合力为0,船舶不再移动或者在小范围内往复抖动的现象.典型的局部极小值问题可以细分为两种情况,见图4.
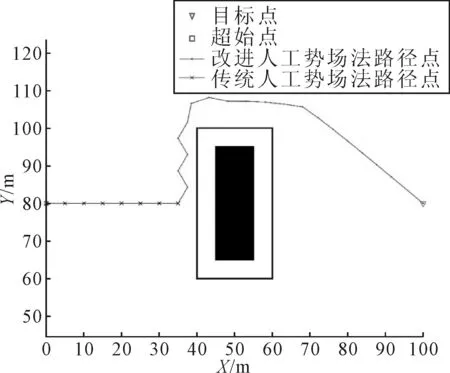
1) 在船舶与目标点之间存在单一障碍物,且船舶、障碍物和目标点处于同一直线.此时,随着船舶逐步向目标点运动,斥力逐渐增大,引力逐渐减小,最终运动到某个斥力与引力大小相近的位置,船舶在该处停止或者在该点处往复抖动导致船舶无法到达目标点.
2) 在复杂障碍物情况下,多个障碍物组成的复杂障碍物环境所产生的总斥力与目标点产生的引力合力为0,导致船舶无法到达目标点,其中最典型的复杂障碍物情况为C形障碍物.

图4 局部极小值问题
对于传统方法出现的局部极小点问题,将情况一与情况二进行分别处理.
针对情况一,其主要原因是船舶、障碍物和目标点三者共线,船舶受的合力平行于该直线,船舶只能沿着该直线运动,导致无法绕过障碍物,只能在障碍物前来回往复运动,该情况同上述狭窄航道抖振问题相似,通过加入艏向角限制,使船舶无法进行大角度折返运动,限制船舶下一点位移,使其离开局部受力平衡状态,从而解决情况一的局部极小点问题.
针对情况二,提出自适应参数调整回溯法对传统方法进行改进.主要步骤见图5.

图5 自适应参数调整回溯算法流程图
其中,局部极小值状态判别为
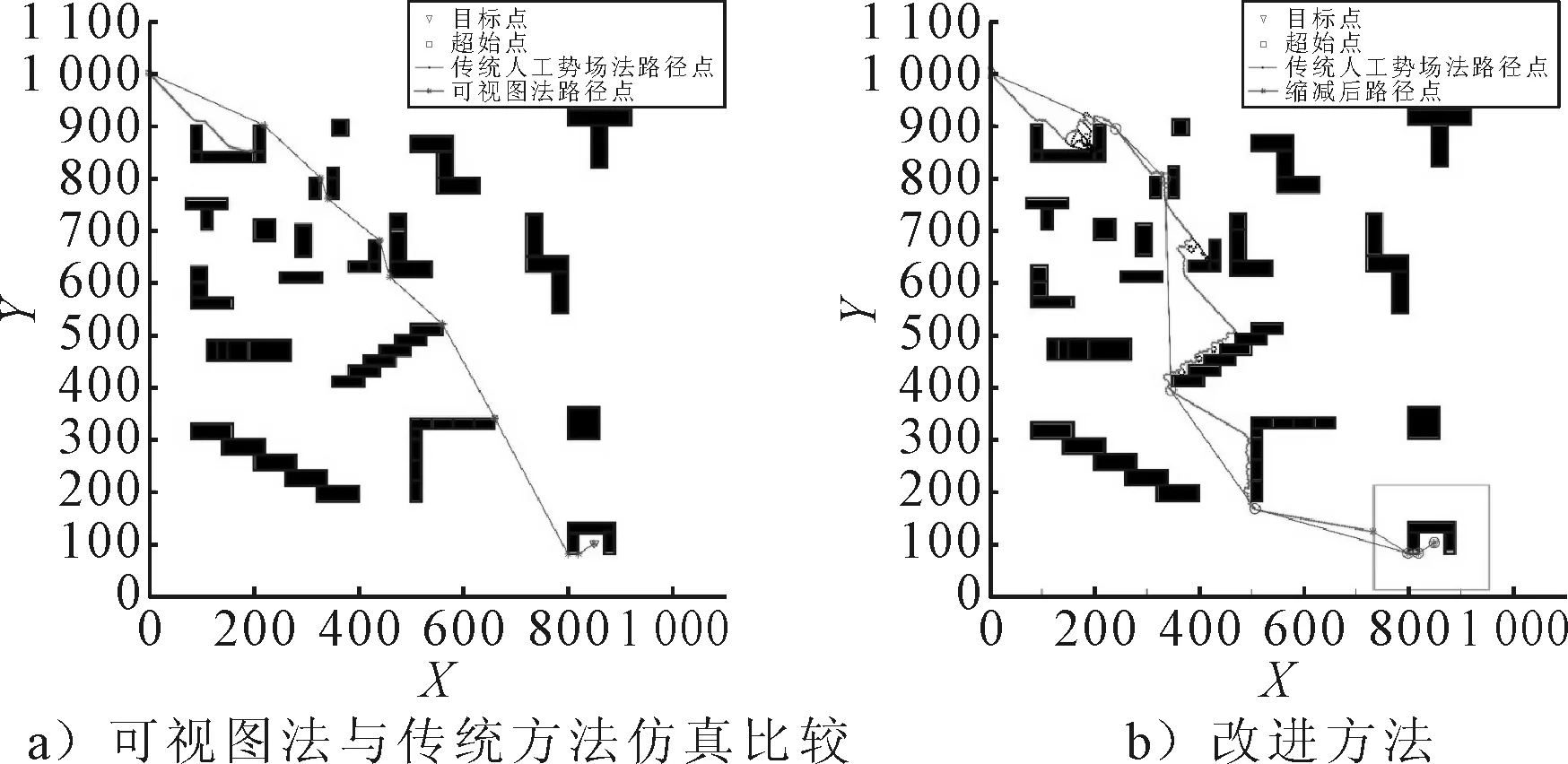
ρ(XJ,XJ-b) (6) 式中:ρ(XJ,XJ-b)为在第J个周期船舶的位置与在第J-b个周期船舶的位置之间的距离;k为极小值判断系数;l为步长. 斥力参数更新公式为 m=tm (7) 式中:t为斥力更新参数. 回溯步长更新公式为 b=b+w (8) 式中:w为回溯步长更新参数. 算法演示见图6. 图6 自适应参数调整回溯算法示意图 通过上述回溯算法,船舶能回溯到若干步长前的位置,在增大斥力参数的情况下,船舶有足够大的力逃离极小值点.若船舶在连续几个周期内,持续处于极小值状态,斥力参数将持续变大,并且随着回溯步数的增加,船舶能够在较短周期内迅速摆脱碰撞状态和逃离局部极小值点;通过设置相应计步器以及计步上限值,船舶能在激活回溯后的连续若干个周期处于正常状态后将斥力参数恢复至初始状态,保证算法在安全状态下的以正常的参数运行. 当目标点周围存在障碍物时,随着船舶向目标点逐步接近,船舶受到的引力减小,斥力增加,将会出现船舶所受斥力大于其所受引力的现象,从而船舶无法到达目标点. 针对目标点不可达问题,本文采用切换可视图法来进行改进.可视图法(V-Graphicic),先构造可视图G(V,E),点集V=V0∪{S,G},V0为各个障碍物的所有端点,S为出发点,G为目标点,E为可见边的集合[11].要求V中任意两点之间连线都不能同所有障碍物存在相交的现象.通过对边赋权值,即可通过搜素算法找出一条从起点到终点的最优路径.可视图法优点是结构简单,不足之处在于随着环境的复杂度上升,其运算时间将会大大加长. 文中提出将人工势场法与可视图法进行结合,具体表示为将船舶的路径规划分为两个阶段,第一阶段采用人工势场法进行规划,当运行至某个周期时,船舶行驶至包含目标点的障碍物的斥力影响范围内,激活切换,将人工势场法算法切换至可视图法,完成剩余阶段的路径规划.该切换策略将整体的环境信息进行划分,为可视图法提供了仅包含第二阶段的小范围的点集环境.通过设置该人工势场法-可视图法切换策略,不仅能够融合人工势场法的实时性好与可视图法的结构简单的优点,还能克服人工势场法目标点不可达以及在复杂环境下可视图法运算时间过长的缺点. 人工势场法在绕开障碍物的时可能会出现过大幅度的避让现象或者在复杂障碍物环境下会出现局部打转等现象导致生成一些不必要的路径点,使生成的路径不是最优.由文献[12]提出的改进方法,设置路径点删减算子,当第i个点pathpointi与第i+2个点pathpointi+2二者相连的线段不会与任意障碍物相交的情况下,删除第i+1个点pathpointi+1,见图7.通过增加路径点删减算子,可以去除人工势场法运行过程中产生的多余路径点,降低规划出的路径总长度. 图7 路径点删减算子示意图 传统方法与改进方法在狭窄航道中的仿真对比结果见图8,其中起始点坐标为(64,0),目标点坐标为(126,160),引力参数k=1,斥力参数m=100,障碍物扩展参数ρe=5,步长l=5,斥力影响范围ρ0=50,最大转向角θ=60°. 图8 狭窄航道情况下仿真比较 由图8可知,传统方法在狭窄航道情况下会出现明显的抖振现象.利用本文提出的增加艏向角限制的改进方法在狭窄航道情况下表现良好,船舶在进入狭窄航道后,不会出现大角度折回现象,从而使船舶能迅速沿岸壁方向稳定前行,有效抑制了抖振现象的产生. 针对情况一下的局部极小值问题分别对传统方法以及改进方法进行仿真比较.结果见图9,其中起始点坐标位置为(0,80),目标点坐标位置为(100,80),引力参数k=1,斥力参数m=200,障碍物扩展参数ρe=5,步长l=5,斥力影响范围ρ0=30,最大转向角θ=60°. 图9 情况一仿真比较 由仿真结果可知,传统方法在船舶运行到第七个步长时陷入局部最小点,无法继续向目标点移动,最后导致路径规划不成功.增加了艏向角限制之后,当船舶运动至局部极小点位置时能以相应限制角度转向,向目标点继续运动,最终成功到达目标点. 针对情况二下的局部极小点问题分别对传统方法以及方法进行仿真比较,仿真结果见图10,其中起始点坐标位置为(0,300),目标点坐标位置为(300,0),引力参数k=1,斥力参数m=500,障碍物扩展参数ρe=5,步长l=5,斥力影响范围ρ0=70,最大转向角θ=60°,回溯步数b=10. 图10 情况二仿真比较 由仿真结果可知,传统方法在进入U形区域中陷入局部极小点.通过增加本文提出的自适应斥力参数回溯法,在经过5次回溯后,船舶能绕过U型障碍物,最终顺利到达目标点. 针对目标点不可达问题分别对传统方法以及改进方法进行仿真比较,仿真结果见图11.其中起始点坐标为(0, 0),目标点坐标为(150,150),引力参数k=1,斥力参数m=200,障碍物扩展参数ρe=5,步长l=5,斥力影响范围ρ0=30. 图11 目标点不可达问题仿真比较 由图11可知,在目标点周围有障碍物存在的情况下,传统方法规划出的路径无法到达目标点,通过采用人工势场法-可视图法结合算法,船舶运行至包含目标点的障碍物斥力范围内时,切换成可视图法,完成剩余阶段的路径规划,顺利到达目标点. 选取算法的初始参数为:起始点坐标位置为(0,1 000),目标点坐标位置为(850,100)引力系数k=1,斥力参数m=500,步长l=5,最大转向角θ=60°,障碍物扩展参数ρe=5,斥力影响范围ρ0=70,回溯步数b=5,极小值判定系数k=0.5,斥力系数更新参数t=5,回溯步数更新参数w=5,分别采用传统方法、可视图法以及改进方法进行仿真,见图12和表1. 图12 复杂地图环境中的传统方法、可视图法和改进方法 表1 算法比较 由图12和表1可知,传统方法在复杂环境中陷入局部极小值导致无法完成剩余路径规划,改进方法与可视图法都能规划成功,在规划的路径长度相差不多的情况下,改进方法耗时比可视图法缩减了10倍. 本文对传统人工势场法存在的狭窄航道抖振问题、局部极小值问题以及目标点不可达问题进行详细分析,针对狭窄航道出现的大角度反向运动,提出设置艏向角限制,有效的抑制了抖振现场的产生;通过设置艏向角限制以及采用自适应参数调整回溯法分别解决了由斥力与引力共线以及由复杂障碍物产生的极小值问题,通过设置人工势场法—可视图法切换策略,在保证算法良好实时性的情况下解决了目标点不可达问题.最后对所提出的各改进方法在Matlab上仿真,结果证明了改进算法的可行性.
2.3 解决目标点不可达问题
2.4 路径点删减算子

3 仿真及结果分析
3.1 狭窄航道抖振现象仿真分析
3.2 局部极小值现象仿真分析

3.3 目标点不可达问题仿真分析

3.4 复杂地图环境仿真分析

4 结 束 语
