基于Box-Cox指数变换改进的ARIMA模型交通流预测方法*
2020-12-17李文勇李俊卓
李文勇 李俊卓 王 涛
(桂林电子科技大学建筑与交通工程学院 桂林 541004)
0 引 言
随着智能交通系统(intelligent traffic system,ITS)的快速发展,智能交通控制与诱导系统成为ITS研究的热门课题.准确的交通流量预测是实现智能交通控制与诱导的前提与关键.为了适当地控制交通,需要采取有效的策略来管理交通流量,改善道路交通拥堵,减少环境污染.
ARIMA模型(auto-regression intergrated moving)对非平稳序列的拟合有较好的适用性,但交通流量日变化特性引起的异方差性,使ARIMA模型的拟合残差被严重低估,最终导致模型的拟合精度受到影响.针对这种问题,很多学者在ARIMA模型的基础上提出改进方法,王晓全[1]提出了一种组合ARIMA-GARCH-M模型,该模型针对时间序列的条件异方差,提出的模型可以有效的消除短期自相关性的引起的条件异方差和随机波动,但对于交通量日变化引起的长期自相关性的异方差不能有效的消除.韩超等[2]提出了基于线性最小方差预报原理Astrom预报算法与ARIMA预测结合的混合预测方法,谭满春等[3-4]利用ARIMA与智能算法结合的方式,提出了小波降噪的ARIMA与支持向量机组合的预测方法,以及ARIMA与人工神经网络结合的交通流量预测方法.然而,由于与智能算法的结合,需要迭代计算,引起计算量大,模型解释性较差的问题[5-6].
文中提出基于Box-Cox指数变换改进的ARIMA模型改进的交通流预测方法,改进算法针对交流流量序列的日变化引起长期自相关因素引起的异方差,推导了方差齐次转换函数,该模型具有方法简单、计算方便、易于解释等优点,能有效的消除长期自相关因素引起的异方差,提高预测精度.
1 ARMA交通流预测模型
自回归移动平均模型(auto-regression and moving average model,ARMA)是一种随机时间序列模型,以最小化协方差矩阵的方式寻找最优的预测值[7-8],相关表达式为
(1)
式中:p,q分别为AR和MA阶数;φi,θj为模型的自回归系数和移动平均系数;εt为随机误差.
由于交通流量具有明显的日变化(季节性)不能满足ARMA模型的平稳条件,ARMA模型不能较好的适用于交通流量预测中[7-9].
ARIMA是差分运算与ARMA模型的组合,通过周期为步长的差分预算,可以消除交通流量的日变化趋势,ARIMA模型为
(2)

图1 ARIMA模型建模步骤
2 改进模型
由于不同时段交通流量方差的不同,E(εt)为同分布的假设仍不能满足,其模型残差往往不能通过噪声检验.因此,本文通过寻找时间序列方差齐次转换函数使E(εt)转化为同一分布,具体实施步骤如下.
步骤1交通流量观察数据的预处理 错误数据的剔除、修复、丢失数据的补充.
步骤2寻找Box-Cox变换参数λ通过对数据的分析发现,Box-Cox变换可以明显地改善交通流量数据的正态性、对称性和方差相等性,Box-Cox变换是对回归因变量的变换,其一般形式为
(3)
这里λ是一个变换参数,对不同数据要确定变换参数λ,使得y(λ)满足
y(λ)=Xβ+e,e~N(0,σ2I)
(4)
一般采用极大似然法确定变换参数,其似然函数为
(5)
式中:J为变换的Jacobi行列式.
(6)
步骤3寻找交通流量均值和方差之间函数关系 在求得Box-Cox变换参数λ后,可以建立交通流量均值与方差的线性回归方程,为
[Var(μt)]λ=aμt+b
(7)
通过采用最小二乘估计的方法,可以求得回归参数a,b.
步骤4寻找方差齐次变换函数 假设有一个转化函数g(·),使转化后g(xt)满足方差齐次条件,即
Var[g(xt)]=σ2
(8)
式中:σ2为常数.
将g(xt)在μt附近作一阶泰勒展开.
g(xt)≈g(μt)+(xt-μt)g′(μt)
(9)
则有:
Var[g(xt)]≈Var[g(μt)+(xt-μt)g′(μt)]
(10)
Var[g(xt)]=[g′(μt)]2Var(xt)
(11)
Var[g(xt)]=[g(μt)]2h(μt)
(12)

(13)
步骤5将交通流量按求得公式进行方差齐次变换,再利用ARIMA模型依次进行差分、定阶、预测、检验.
步骤6将预测结果按g-1(μt)进行还原.
3 实例验证
为检验本文模型交通流量预测的精度,利用重庆市北培路东出口2600号微波检测器2017年7月19日—8月17日的交通流量观测数据进行验证,传感器以5 min为采样周期,每天共采集288组.
在数据预处理后,要探讨不同时间段观察数据方差和均值之间的关系.利用似然法求得Box-Cox转换参数λ=0.101 010 1,再利用最小二乘法求得线性回归模型回归系数,得到交通流量数据的方差和均值之间的关系.
[Var(μt)]0.101 010 1=1.856 617+0.001 195μt
(14)
根据回归分析结果绘制残差图,见图2.结果显示经过Box-Cox转换的观测数据能被回归模型较好的描述.
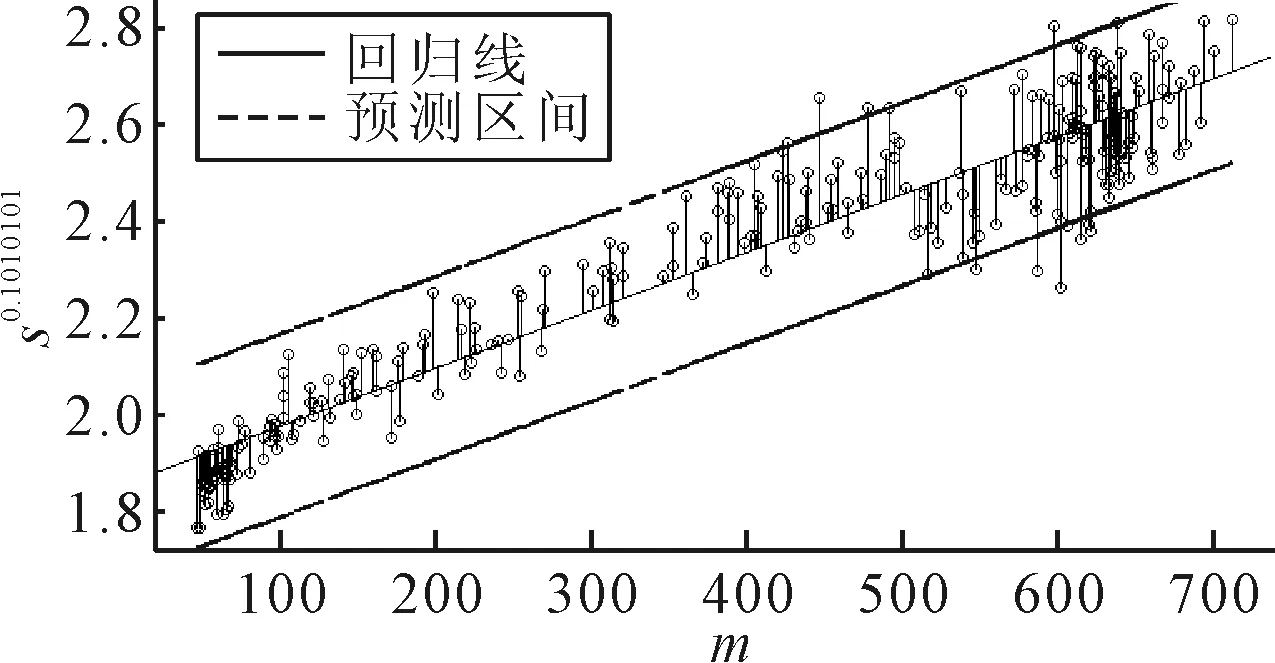
图2 回归分析残差图
得到回归函数后,进行方差齐次变换,代入式(13),计算的方差齐次函数为
(15)
由于交通流量序列存在固定日周期变化趋势,对观测交通流量序列进行一阶288步差分运算,以消除交通流量日变化对交通预测的影响.
为确定ARIMA模型自回归阶数p和移动平均阶数q,绘制并观察自相关系数和偏自相关系数图,见图3.
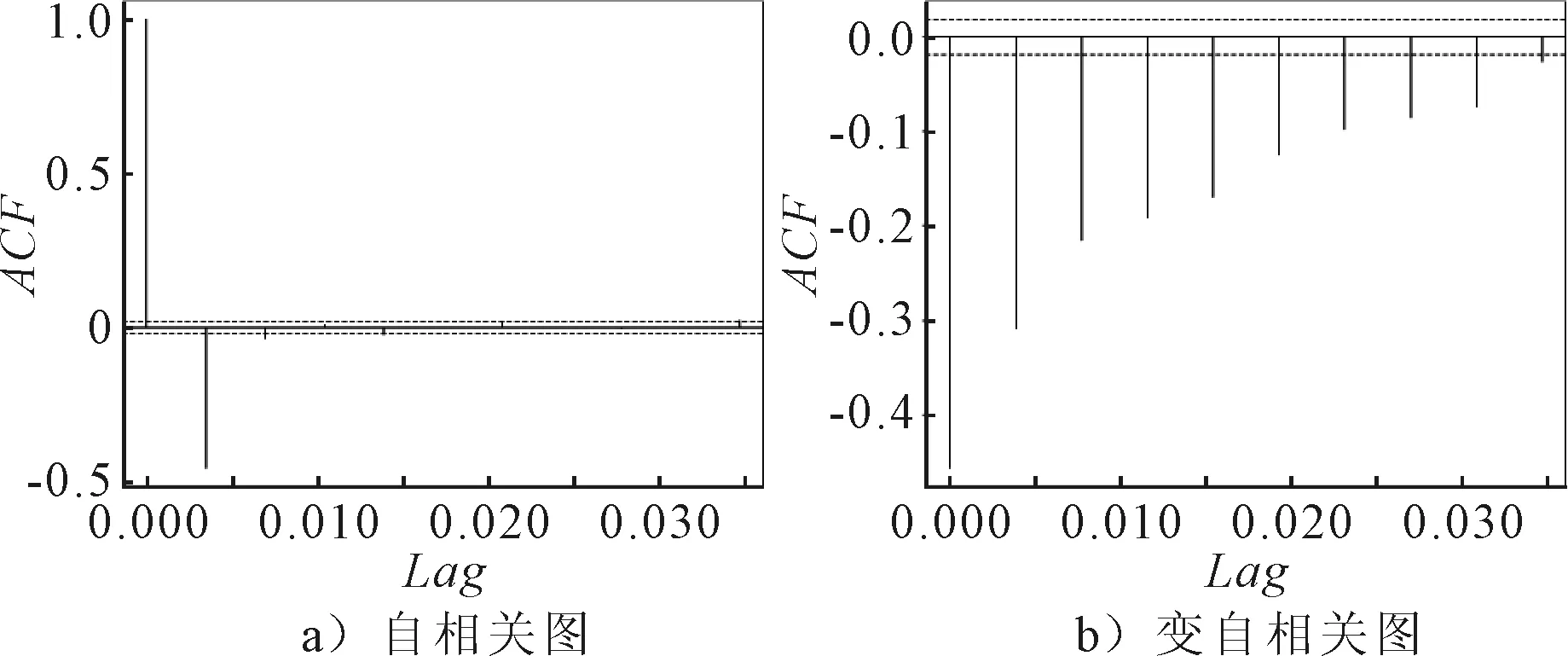
图3 交通量序列自相关图、变自相关图
根据时间序列自相关图与偏自相关图可以判断自相关系数2阶截尾、偏自相关系数拖尾,选择AR(2)模型对其进行拟合,计算得自相关系数AR(1)=0.201 8,AR(2)=0.114 0,预测模型为
(1-B288)(1-B)xt=
εt~N(0,0.146 5)
(16)
利用求得预测模型计算出预测交通流量,最后利用g-1(μt)还原交通流量时间序列,并绘制预测图,见图4.
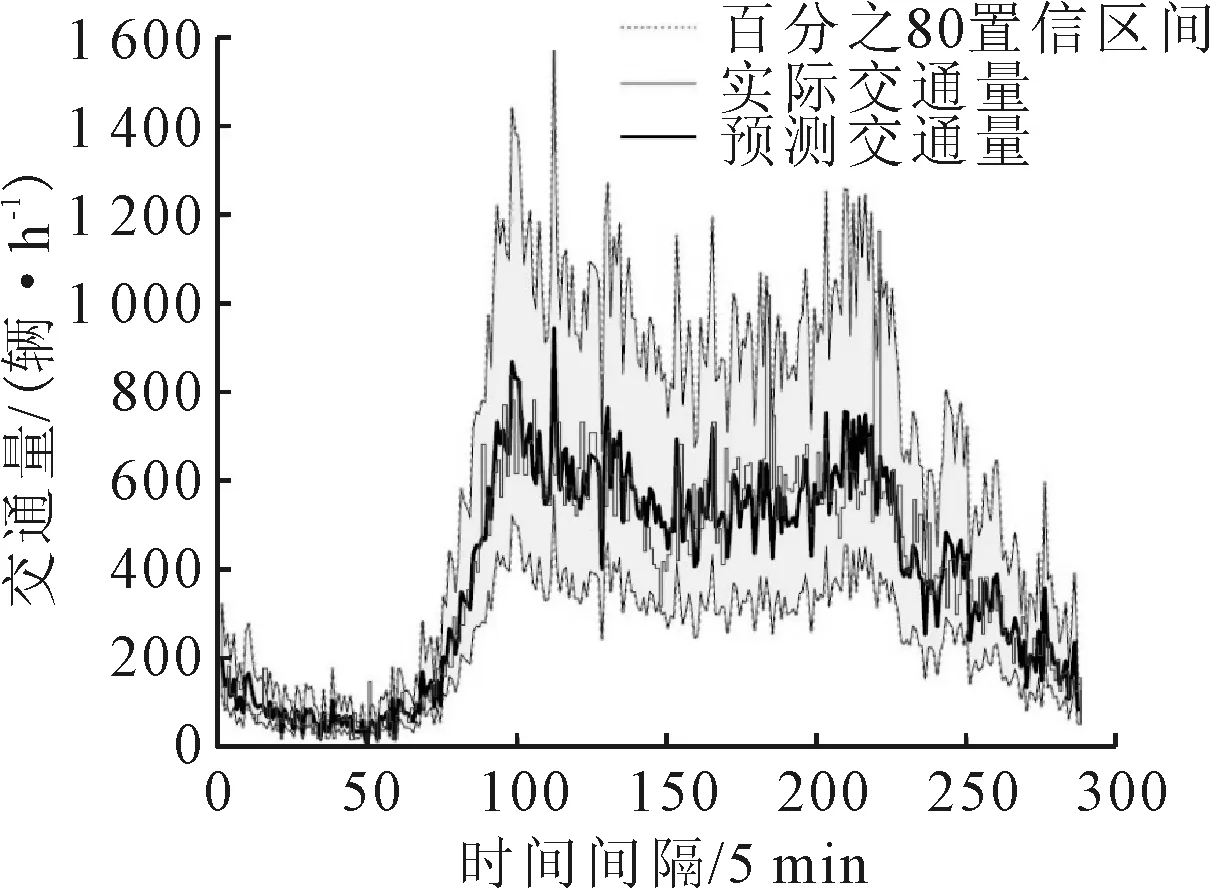
图4 改进ARIMA模型预测结果
4 模型对比分析
利用HlotWinter模型与改进的ARIMA模型的预测结果进行对比.HoltWinter预测结果见图5.

图5 HoltWinter模型预测结果
为了能评价和比较仿真实验结果,使用平均绝对百分误差(mean absolute percentange error,MAPE)和均方根误差(root mean square error,RMSE)预测指标:
(17)
(18)
ARIMA预测方法与HlotWinter预测方法的评价指标见表1.

表1 预测评价指标对比
通过对比MAPE和RMSE评价指标,结果表明改进的模型整体上优于HoltWinter模型,证明本文模型在进行交通流量预测中预测精度较高.同时,由于改进的ARIMA模型考虑了不同时间段的方差的不同,在低流量时刻ARIMA模型具有更加精确的置信区间.
5 结 论
1) 提出的改进的ARIMA模型具有较高的预测精度,消除了交通流量序列长期自相关引起的异方差性,相比于非平稳预测方法HoltWinter模型,其整体预测结果更加可靠.
2) 由于考虑了交通流量序列长期自相关引起的异方差性,在低流量时段改进的ARIMA模型的方差更小,能提供更准确的置信区间.
3) 提出的改进模型主要针对交通流量日变化的长期自相关引起的异方差,对于具有短期自相关性的条件异方差没有充分考虑.对于随机交通事件,引起的某些时段交通量波动,如何选择更加合适的改进方式是值得进一步研究的课题.
