探究高中数学解析几何———以圆锥曲线与直线的位置关系为例

◇ 江苏 蔡 祥

(作者单位:江苏省盐城市伍佑中学)

圆锥曲线证明问题一直是数学考试中的必考题目,纵观历年高考,这类问题都是以解答题的形式出现.由于圆锥曲线问题具有抽象性、计算过程较复杂、涉及的知识面广泛、应用能力较强,对于学生来说有一定的难度.本文以圆锥曲线与直线的位置关系为例,分析教学现状,并提出有效的教学模式与手段.

1 教学现状分析

1)教学模式基本上教师是以制作课件、电子白板教学为主,虽然范围广泛,但都还是以传统的思维进行教学,以教师自己为中心,导致学生无法跟上教师的教学思路.

2)对于学生来说,课堂缺少灵活性、激励性,学生不积极主动学习,对曲线几何理论的掌握不够充分,长此以往,导致恶性的循环,碰上综合性较强的问题,就会“想破脑壳”也无法动笔解答.

2 解析几何问题的分析角度

图1

3 真题展示分析

例设椭圆的右顶点为A,上顶点为B,已经椭圆的离心率为

(1)求椭圆的方程;

(2)设直线l:y＝kx (k＜0)与椭圆交于P,Q 两点,l与直线AB 交于点M,且点P,M 均位于第四象限.若△BPM 的面积是△BPQ 面积的2 倍,求k的值.

(2)设点P 的坐标为(x1,y1),点M 的坐标为(x2,y2),由题意可知x2＞x1＞0,点Q 的坐标为(－x1,－y1).由△BPM 的面积是△BPQ 面积的2倍,可得|PM|＝2|PQ|.

从而x2－x1＝2[x1－(－x1)],即x2＝5x1,易知直线AB 的方程为2x＋3y＝6.

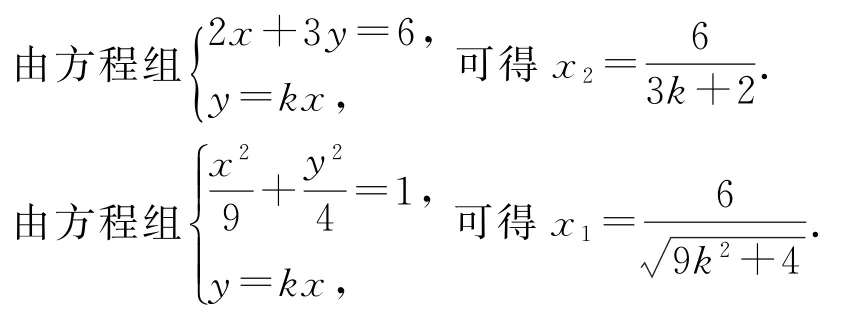
由x2＝5x1,可得平方整理得18k2＋25k＋8＝0,解得

此题考查的是圆锥曲线与直线的位置关系.是历年高考中常见的考点,基本上以解答题的形式出现.解答此类题目首先要把两个三角形的面积关系转化为点P 与M 的横坐标间的关系,进而得到关于k 的方程,然后应用根与系数的关系进行求解.

圆锥曲线与直线的位置关系等几何内容无疑是高考的重点和难点.它对学生空间思维、理解、函数应用等能力都有很高的要求,考核内容涉及很多知识点.因此,教师在平时的教学当中一定要让学生听懂、理解,用画图、演示等方式,让学生动起来,让学生产生兴趣才是关键.