例析万有引力与重力的区别和联系

◇ 江苏 包赛华

(作者单位:江苏省启东市大江中学)

近年来,新的考试大纲明确规定:“万有引力定律及其应用”属于第Ⅰ类要求,并再次阐明“万有引力定律及其应用”是高中物理的核心知识.在高考全国卷Ⅰ、Ⅱ的试题中,“万有引力定律”和“万有引力定律的应用”几乎都以选择题的形式出现,且难度不小,得分率很低,为什么会出现这种情况呢?

首先,万有引力定律问题对学生理解能力和空间想象力要求很高,其次是学生对万有引力和重力的联系与区别尚不了解,在中学阶段,关于万有引力和重力有两个观点:一是重力是万有引力的一个分力;二是重力是地球对物体的引力,哪种观点是正确的呢?笔者认为,在某些情况下,这些观点都是正确的,分歧的根本原因在于参考系的选择.

1 地球表面的重力与万有引力之间的区别和联系

生活中重力有很多应用,我们通常所说的重力为传统的重力,传统重力必须以地面为参考系.将物体悬吊在弹簧测力计上并保持静止,物体在重力G 和弹簧弹力F 两个力的作用下保持平衡,满足平衡关系G＝F.实际上,这是重力的起源,并且今天仍在使用.后来人们发现地球在不停地自转,所有相对静止的物体(两极除外)实际上都在做匀速圆周运动,物体存在自转加速度,并不是处于平衡状态.牛顿发现万有引力定律后,这个问题得到了很好的解释.

如果以地心为参考系来分析地球表面的重力,又会得到怎样的结论呢?

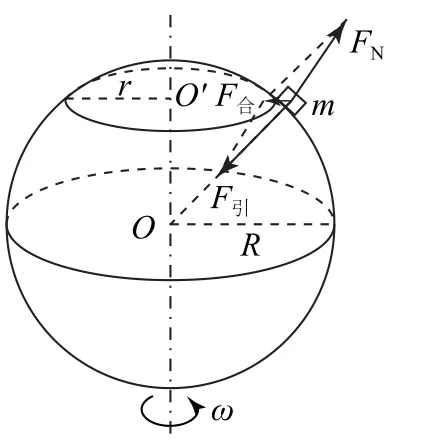
图1

图2

如图1所示,放在地球北半球某地的物体m 静止在水平地面上,真实情况中它只受万有引力和地面的支持力,这两个力的合力F 指向物体做圆周运动的圆心O′,这也是向心加速度的方向.这里要特别强调的是,由于离心运动的缘故,地球其实是一个椭球体,FN的方向和F引不共线(两极和赤道除外).合成法分析受力简洁明了,但是不利于运算,而分解法可以很好地说明问题.如图2,可以将F引沿半径和FN的反方向分解,已知合力和两分力的方向,分解具有唯一性,其中F2一定和FN相等,F1充当向心力,不论物体在地球表面的什么位置,我们都可以这样处理,因此,人们把F2命名为重力G.这样看来,重力就是万有引力的一个分力.重力其实是一个“虚拟力”.根据牛顿第二定律为物体做圆周运动的轨道半径,其中F2＝G＝mg,g 为当地地表处的重力加速度.

为了说明地球表面处重力和万有引力大小的关系,在这里做一个定量计算.假设一质量m＝50kg的人站在赤道上,已知地球质量M ＝6.0×1024kg,地球半径R＝6.4×106m,地球自转周期为24h,万有引力常量G＝6.67×10－11N·m2·kg－2,它所受的万有引力所需的向心力F＝向1.7N,所受的重力G＝FN＝486.8N.这里可以看出,物体在赤道上随着地球自转所需要的向心力实在太小,在地球表面的其他地方所需要的向心力那就更小了.所以通常可以忽略,认为这就是黄金代换,一个非常重要的表达式.重力之所以和万有引力有差别,原因是地球存在自转.

2 高空中重力与万有引力的区别和联系

上文我们解决了地球表面物体的重力和万有引力的关系,那么当物体远离地球表面时,它们的关系又如何呢? 我们必须明确测传统重力时,不管物体是在地表还是高空,一定是以地表为参考系,挂上重物的弹簧测力计稳定且相对地表静止时,弹簧测力计的读数显示的才是传统重力的大小.

那么传统意义上的重力和万有引力在高空中有什么样的关系呢? 我们可以设想这样一个情境,假如有一天,人们在赤道和地球同步轨道空间站之间建立一座电梯,人们乘坐电梯就可以达到空间站.假设某人乘坐该电梯停在离赤道表面h 高处时,该人还是绕着地心做匀速圆周运动,根据牛顿第二定律有

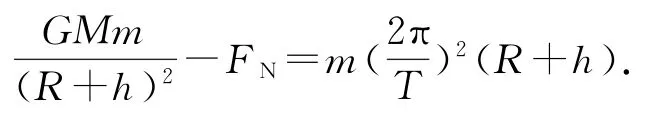
为了说明高空处重力和万有引力的大小关系,我们在这里也做一个定量计算.假设乘坐电梯的人质量m＝50kg,其他的条件如前文,结果如表1所示,可以看出当物体高度h 在0～2R 时,重力和万有引力还是可以看作近似相等.

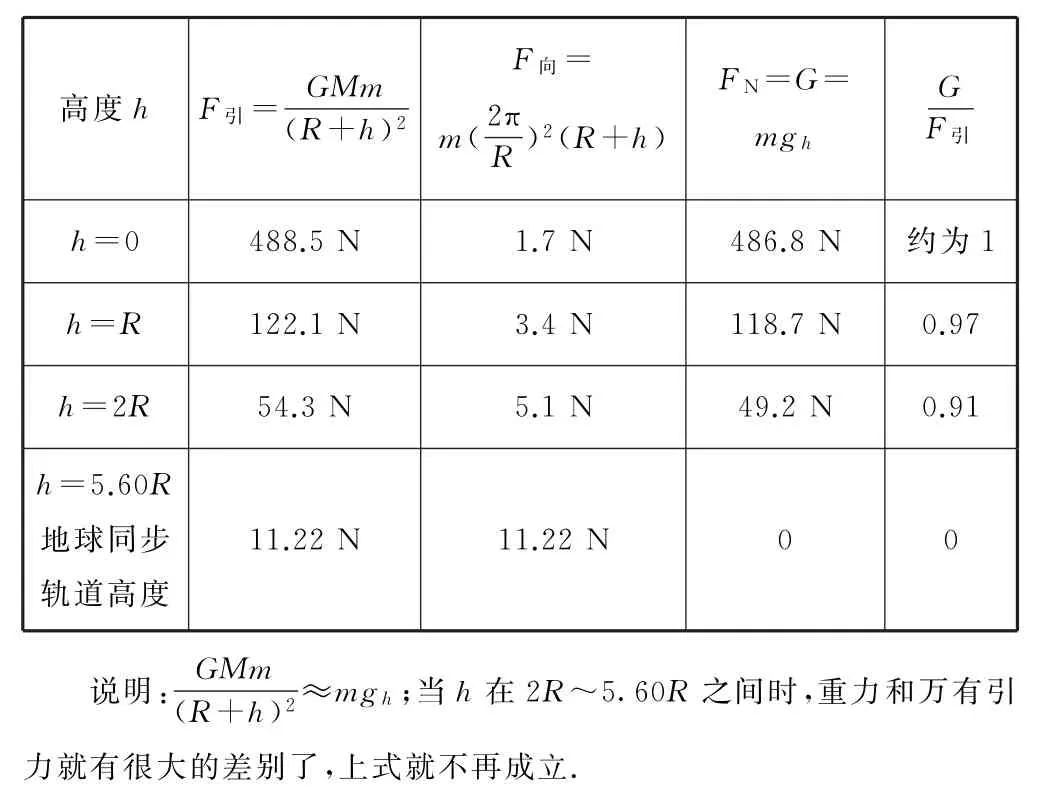
表1

这里特别要提出的是,当电梯停在同步轨道时,人的重力为0,这和实际情况是符合的.但是对于那些非同步轨道的人造卫星,按照上面的理论,其传统重力是不为0的,但是这些卫星包括它里面的物体的确是处于完全失重状态.非同步卫星相对于地球表面不是静止的,并且重力的定义不再适用于理解做匀速圆周运动的卫星的重力.将卫星受力称为“传统重力”毫无意义.因此,人们习惯上也将卫星受到的引力描述为重力.从卫星上物体的失重情况来看,表观重力为零,实际重力指与常规重力不同的重力.

总之,以上两个观点并无矛盾之处,至于什么情况下考虑重力,什么情况下考虑万有引力,则需要分在哪个参考系中和物体在哪个区域来看待问题,在地心参考系中需要考虑的是万有引力,在地面参考系中一般只需要考虑重力.传统意义上的重力实际上是引力的一部分,对于以恒定速度做圆周运动的卫星,人们通常还将卫星受到的万有引力描述为重力.