人船模型解题研究

◇ 湖北 戈 菲

(作者单位:湖北省宜昌市葛洲坝中学)

人船模型问题不仅仅是动量守恒问题,更是力学综合问题,此类问题涉及动量、能量、力与运动等知识,解题方法有规律可循.本文通过对例题的分析,总结人船模型的解题方法,希望对师生有所帮助.

1 例题及解析

例1如图1所示,质量为M 的物体静止于光滑水平面上,其上有一个半径为R 的光滑半圆形轨道,现把质量为m 的小球自轨道左侧最高点由静止释放,问:(1)摆球运动到最低点时,小球与轨道的速度是多少? (2)轨道的振幅是多大?

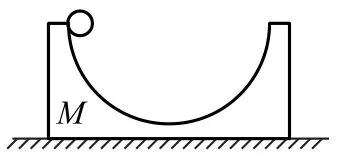
图1

(1)设小球到达最低点时,小球与轨道的速度分别为v1和v2,根据系统在水平方向动量守恒,得mv1＝Mv2,又由系统机械能守恒得

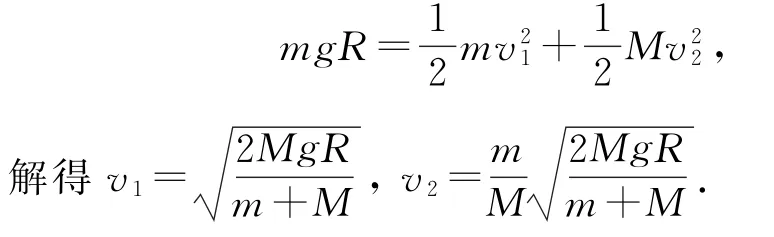
(2)当小球滑到右侧最高点时,轨道左移的距离最大,即振幅A.由人船模型得mx＝My,x＋y＝2R,解得即振幅

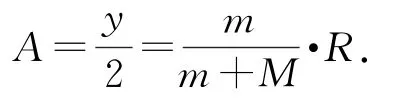
例2(2018年新课标卷Ⅰ)质量为m 的烟花弹获得动能E 后,从地面竖直升空.当烟花弹上升的速度为零时,弹中火药爆炸将烟花弹炸为质量相等的两部分,两部分获得的动能之和也为E,且均沿竖直方向运动,爆炸时间极短,重力加速度大小为g,不计空气阻力和火药的质量.求:(1)烟花弹从地面开始上升到弹中火药爆炸所经过的时间;(2)爆炸后烟花弹向上运动的部分距地面的最大高度.

(1)设烟花弹在地面时的速度为v0,则E＝烟花弹竖直上抛,则联立可得

(2)设烟花弹上升高度为h1后爆炸,根据机械能守恒定律可得E＝mgh1.爆炸后两者质量均为竖直方向根据动量守恒定律可得,二者的速度相等,均为v,二者的动能均为设向上运动的部分继续上升的高度为h2,根据能量守恒定律得联立以上各式可得

2 解题方法总结

动量守恒定律是高考的必考内容,而人船模型是动量守恒定律的重要题型之一.认识模型、举一反三、善于迁移与变通对于试题的解决有很大的帮助.本文总结解题方法如下:

1)掌握人船模型的3个条件:a)多个物体组成的系统初状态静止;b)多个部分相对运动过程中,系统所受合外力为零或者某一方向上合力为零;c)多个部分对地位移之和为定值.满足以上3个条件的问题,可以视为人船模型问题.

2)掌握解决问题的必要物理知识,加强对物理概念、物理规律的认识和理解.例如学习动量守恒定律,一要知道动量守恒定律如何而来;二要知道动量守恒定律的内容、公式;三要知道公式成立的条件,即合外力为零,或者合外力远小于内力;四要知道公式的性质,例如动量守恒定律的矢量性、瞬时性等.

3)掌握人船模型的核心内容及涵盖范围.人船模型以动量守恒定律为核心考点,以运动、受力、能量为覆盖点,构成“一核三翼”的力学综合问题.

4)掌握人船模型的常见变式.人船模型的起源是人在船上从一端走到另外一端,这是常见的问题.其变式还有:a)竖直方向上的人船模型(例2);b)曲线运动中的人船模型(例1);c)多物体的人船模型.掌握原型并将规律灵活应用于变式之中,可以提高解决问题的速度和准确率.

总之,人船模型是动量守恒问题中的一种常见模型,与子弹打木块模型、反冲模型、弹簧—物块模型等的解题方法有相似之处,但也有不同之处.我们要做好知识储备,了解人船模型的应用条件、掌握人船模型的核心考查点,灵活处理变式问题,从而突破此类问题的学习难点.