“椭圆”的高频考点例析

◇ 甘肃 何慧娴

(作者单位:甘肃省甘谷县第二中学)

椭圆问题可以很好地考查学生数学运算能力、逻辑推理能力、数形结合思想、函数与方程思想以及化归与转化思想,同时,能考查考生的综合思维能力,具有很好的选拔功能,因此在高考和其他各类考试中备受命题专家的青睐.本文拟通过归类举例的形式,具体说明“椭圆”的高频考点,旨在帮助同学们厘清常用解题思维,提高处理有关椭圆问题的能力.

1 考查与焦点有关的最值问题

处理椭圆中与“焦点”有关的最值问题时,往往需要紧扣椭圆的“定义”和“图形”,灵活分析.这类问题侧重考查转化思想与数形结合思想在解题中的综合运用.

例1已知是椭圆内的点,M 是椭圆上的动点,则|MA|＋|MB|的最大值是________.

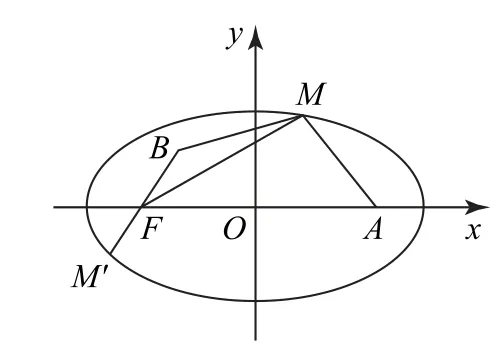
图1

如图1 所示,易知点A 恰好为椭圆的右焦点,设左焦点为F(－4,0),连接BF,由椭圆的定义知|MA|＋|MB|＝2a ＋|MB|－|MF|.又易知当点M,B,F 在同一条直线上(且点M 在线段BF 的延长线上),即点M 与点M′重合时,|MB|－|MF|取得最大值,故|MA|＋|MB|的最大值是|M′A|＋|M′B|＝(|M′A|＋|M′F|)＋|FB|＝2×5＋2＝12.

2 考查求解椭圆的离心率

2)方程法:根据条件先得到关于a,b,c 的齐次等式,再结合b2＝a2－c2转化为关于a,c 的齐次式,然后将齐次式两边同除以a 或a2可转化为关于e 或e2的等式,最后通过解方程即可求得e 的值.

例2椭圆的左、右焦点分别为F1,F2,焦距为2c,若直线与椭圆Γ 的一个交点M 满足∠MF1F2＝2∠MF2F2,则该椭圆的离心率等于________.

3 考查 “设而不求”解题策略的应用

直线与椭圆的最值、定值、定点问题是高频考点,需要运用“设而不求”技巧以及相关解析几何知识加以灵活求解,同时,需要关注“数形结合”“分类与整合”“等价转化”等思想在解题中的灵活运用.

例3从圆O:x2＋y2＝5上任意一点P 作椭圆的两条切线,切点为A,B,试探究∠APB 的大小是否为定值.若是定值,求出这个定值;若不是请说明理由.

当两切线之一的斜率不存在时,根据对称性,设点P 在第一象限,则此时点P 的横坐标为代入圆的方程得点P 的纵坐标为此时两条切线方程分别为

总之,关注“椭圆”的高频考点,有利于巩固所学知识、方法在解题中的灵活运用能力,有利于提升直观想象、数学运算以及逻辑推理等核心素养.