高考数学开放性问题的探索

◇ 山东 刘文静

(作者单位:山东省滨州市第一中学)

高考一直在进行题型改革的探索,2019年11月末,山东省组织高三学生进行了一次统一的模拟考试,在第17题(第一个解答题)中,出现了从三个条件中选取一个条件组成一道题目的试题,属于条件开放(半开放)性问题.问题难度虽然不大,却改变了以往题目固定的形式.

开放性问题是指那些答案不唯一或在设置的条件上要求学生能够进行多角度、多方面、多层次探索的问题.因此开放性问题包括条件开放型、结论开放型和完全开放型问题.

1 条件开放(半开放)型

例1在①b1＋b3＝a2,②a4＝b4,③S5＝－25这三个条件中任选一个,补充在下面的问题中,若问题中的k 存在,求k 的值;若k 不存在,请说明理由.

设等差数列{an}的前n 项和为Sn,{bn}是等比数列,_______,b1＝a5,b2＝3,b5＝－81,是否存在k,使得Sk＞Sk＋1且Sk＋1＜Sk＋2?

分析本题考查数列知识.

因为在等比数列{bn}中,b2＝3,b5＝－81,所以其公比q＝－3,从而bn＝b2(－3)n－2＝3×(－3)n－2,从而a5＝b1＝－1.

若存在k,使得Sk＞Sk＋1,即Sk＞Sk＋ak＋1,从而ak＋1＜0;同理,若使Sk＋1＜Sk＋2,即Sk＋1＜Sk＋1＋ak＋2,从而ak＋2＞0.

若选①:由b1＋b3＝a2,得a2＝－1－9＝－10,所以an＝3n－16,当k＝4 时,满足a5＜0 且a6＞0成立.

若选②:由a4＝b4＝27,且a5＝－1,所以数列{an}为递减数列,故不存在ak＋1＜0且ak＋2＞0.

例2已知△ABC 满足________,且求sinC 的值及△ABC 的面积.

分析这类题目难度并不大,选一个合适的条件,转化为封闭式问题即可,重点还是基础知识的掌握.

本题不可选择②作为补充条件.若选①,解答如下.

在△ABC 中,A＋B＋C＝π,所以

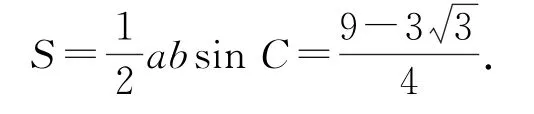
若选③,解答如下.

因为在△ABC 中,A＋B＋C＝π,所以

2 结论开放型

例3(2018年北京卷理13)能说明“若f(x)＞f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是________.

分析本题主要考查函数的单调性,只要满足f(x)＞f(0)对任意的x∈(0,2]都成立,且函数f(x)在[0,2]上不是增函数即可.如f(x)＝sinx,答案不唯一.

例4对于中心在原点的双曲线,给出下列三个条件:

① 离心率为2;②一条渐近线的倾斜角为60°;③实轴长为4,且焦点在x 轴上.写出符合其中两个条件的一个双曲线标准方程________.

分析本题主要考查双曲线的性质,三个条件任选两个都可以求出双曲线标准方程,难度系数不大,答案不唯一.

3 全部开放型

例5(2019年北京卷)已知l,m 是平面α 外的两条不同直线.给出下列三个论断:

①l⊥m;②m∥α;③l⊥α.

以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:_______.

分析若l⊥α,l⊥m,则m∥α,显然①③为条件②为结论是正确的命题;若l⊥m,m∥α,则l∥α,l与α 相交但不垂直都可以,故①②为条件③为结论是不正确的命题;若l⊥α,m∥α,则l 垂直α 内所有直线,在α 内必存在与m 平行的直线,所以可推出l⊥m,故②③为条件①为结论是正确的命题.

高考试题所涉及的事物会随着发展而变化,问题的类型、条件也被不断地创造和完善.解决这种开放型问题就是要改变解决封闭式问题的固定思维,然后再用所学知识进行求解.

链接练习

1.α,β 是两个不同的平面,m,n 是平面α 及β 之外的两条不同的直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中的三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题.

2.在等差数列{an}中,已知a6＝12,a15＝36.若______,求数列{bn}的前n 项和.在①bn＝(－1)n·an,②bn＝③bn＝2an·an这三个条件中任选一个补充在第(2)问中,并对其求解.

链接练习参考答案

1.依题意可得以下四个命题:(1)m⊥n,α⊥β,n⊥β,则m⊥α;(2)m⊥n,α⊥β,m⊥α,则n⊥β;(3)m⊥α,n⊥β,m⊥n,则α⊥β;(4)α⊥β,n⊥β,m⊥α,则m⊥n.不难发现,命题(3)和(4)为真命题,而命题(1)和(2)为假命题.故填上命题(3)或(4).