Analytical and numerical studies for Seiches in a closed basin with bottom friction

I. Mgdlen*, H.Q. Rif'tin, A. Muditr A. Mtin

a Faculty of Mathematics and Natural Sciences, Bandung Institute of Technology, Bandung 40132, Indonesia

b Center for Coastal and Marine Develoment, Bandung Institute of Technology, Bandung 40132, Indonesia

Keywords:Wave resonance Closed basin Bottom friction Natural resonant period Shallow water equations

ABSTRACT A standing wave oscillation in a closed basin, known as a seiche, could cause destruction when its period matches the period of another wave generated by external forces such as wind, quakes, or abrupt changes in atmospheric pressure. It is due to the resonance phenomena that allow waves to have higher amplitude and greater energy, resulting in damages around the area. One condition that might restrict the resonance from occurring is when the bottom friction is present. Therefore,a modified mathematical model based on the shallow water equations will be used in this paper to investigate resonance phenomena in closed basins and to analyze the effects of bottom friction on the phenomena. The study will be conducted for several closed basin shapes.The model will be solved analytically and numerically in order to determine the natural resonant period of the basin,which is the period that can generate a resonance. The computational scheme proposed to solve the model is developed using the staggered grid finite volume method. The numerical scheme will be validated by comparing its results with the analytical solutions. As a result of the comparison,a rather excellent compatibility between the two results is achieved. Furthermore, the impacts that the friction coefficient has on the resonance phenomena are evaluated. It is observed that in the prevention of resonances, the bottom friction provides the best performance in the rectangular type while functioning the least efficient in the triangular basin. In addition,non-linearity effect as one of other factors that provide wave restriction is also considered and studied to compare its effect with the bottom friction effect on preventing resonance.©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Seiches are standing waves oscillating in enclosed bodies of water, such as lakes or inland seas, with physical characteristics resembling the vibrations of an elastic membrane. Typically,seiches occur when water is pushed from one end of the enclosed basin to another by vigorous winds or sudden changes in atmospheric pressure. When the wind stops or the atmospheric pressure normalizes, the water then rebounds back to the part of the basin it was pushed from and continues to oscillate for some time afterwards. The dimensions of the basin where the seiches occur uniquely determine the frequency of the seiche in question. Seiches are capable of causing devastating amounts of destruction. Not only it is possible for the oscillations to exceed 3 m, the currents associated with them can also damage the body structures of the basin. The destructive capabilities of seiches are so noteworthy that names for them have been coined by people living near the places where they often cause harm, such as"abiki" for the seiches of the Nagasaki Harbor in Japan and "rissaga" for the seiches of Ciutadella Harbor in Spain.

Rabinovich [1] and Wilson [2] have explored resonance phenomena in closed basins of various geometric shapes using experiments. The results of these investigations have been used by engineers in related fields. The natural resonant period of a seiche in a closed rectangular basin has already been derived analytically by Wilson [2]. Nevertheless, many of the basins have non-regular geometric forms and the bottoms are constructed of rough material. Hwang and Tuck [3] have derived analytical solutions for basins of undefined plan shape and constant depth by presenting the solution as a superposition wave source utilizing the Huygen's-type method. Lee [4] has addressed the same issue by formulating the solution as an integral equation and defining the basin shape with a piece-wise linear boundary in a matrix equation. This study was extended by Gerber [5] to consider the dissipation effect, but only for fixed depth basins. In a previous study, we have also analytically derived expressions for natural resonant periods of seiches in semi-closed and closed triangular and parabolic basins [6–8]. However, works in the existing literature above do not take into account the friction force that exists between the water and the basin's material. There are few researchers who have studied water flows and resonant waves in an enclosed or/and semi-closed basin that involve the existence of wind and friction, such as in Refs. [9, 10] where the problem have been investigated experimentally. Others, for example in Refs. [11, 12] have studied the issue using numerical approach, while in Refs. [13, 14], analytical methods are presented to model wave propagation in basin where bottom friction is concerned. However, none of the studies addressed the question of how to estimate the natural resonant period, which is when the resonance happens, analytically or numerically.

So far, engineers in charge of designing artificial lakes or reservoirs use existing results from laboratory experiments to guide them in estimating the natural resonant period of seiches in the structures they aim to build. These results are also complemented by previous analytical work investigating seiche in closed basins of regular shape and constant depth. In our current research, we focus on the effect that rough materials used in the construction of human-made lakes can have on the resonant frequency of seiches. The friction exists due to the movement of the wave over rough materials that line the beds of closed basins. Common human-made basins for holding water include dammed valleys, where basins are mostly formed by the natural topography of the area. Depending on the characteristics of the valley, the basin formed by building a reinforced concrete wall to close it may have a triangular or rectangular shape.Other human-made water basins, such as quarry lakes, are formed through excavation and often form closed parabolic basins. The materials that make up each basin as well as bottom sediments and organic materials that settle from surface water provide resistance to the motion of water, which causes a friction force to come into play.

This bottom friction will produce a dissipation effect on waves that limit wave height growth caused by the resonance.However, there is in fact another factor that can facilitate this restriction, which is the non-linearity effect of the waves. It is a good idea to compare both factors' capability to determine which one has the bigger effect than the other in preventing the resonance phenomenon. However, non-linear equations are difficult to be solved analytically. Therefore, in this study, we will only use the analytical approach to solve the linear model, which is used to study the bottom friction effect. In addition, to compare the effect of the friction and non-linearity, numerical simulations will be conducted for two cases: one with bottom friction using the linear model and the other one with non-linear term included in the friction-less equations. Both linear and non-linear model are developed based on the shallow water equations.We will solve the linear model analytically and numerically for three different shapes of basin, which are rectangular, triangular,and parabolic, resulting in the expressions for the natural resonant period when friction is present. The non-linear model will only be solved numerically to compare the effect of the waves non-linearity and bottom friction on reducing wave height.Therefore, we formulate two numerical schemes, each to approximate the linear model and non-linear model for more general use in cases of arbitrary geometry. The numerical schemes that we implement here are constructed using the staggered finite volume method that has been explained briefly in Refs.[15–23].

Here, we will briefly explain about the formulation of our mathematical model to simulate resonance phenomenon in a closed basin when bottom friction is involved. As stated previously, we will only consider the bottom friction in the equations to provide resistance to the resonance phenomenon, while the other feature, which is the non-linearity effect, will be discussed later on. The visualization of the model we used can be seen in Fig. 1. As described in the figure, we assume that the bottom friction is existing in the topography of the basin withCfdenotes the friction coefficient. Since the basin is closed, instead of entering the basin, the wave is induced by an external forces given to the basin, such as strong wind or vibration caused by earthquake. For a relatively small closed basin, such as a bowl or glass, the external forces generated could be in the form of shaking, hitting, or just a few minor movements. Here, we presume that the forces are received at the left end of the basin, which then stimulates a wave that propagates to the right direction.Moreover, η (x,t) expresses the wave elevation,u(x,t) represents the horizontal velocity, whileh=η+ddenotes the total water depth. In this case, we assume that η is quite small relati ve toh, thus the total water depth becomesh≈d.

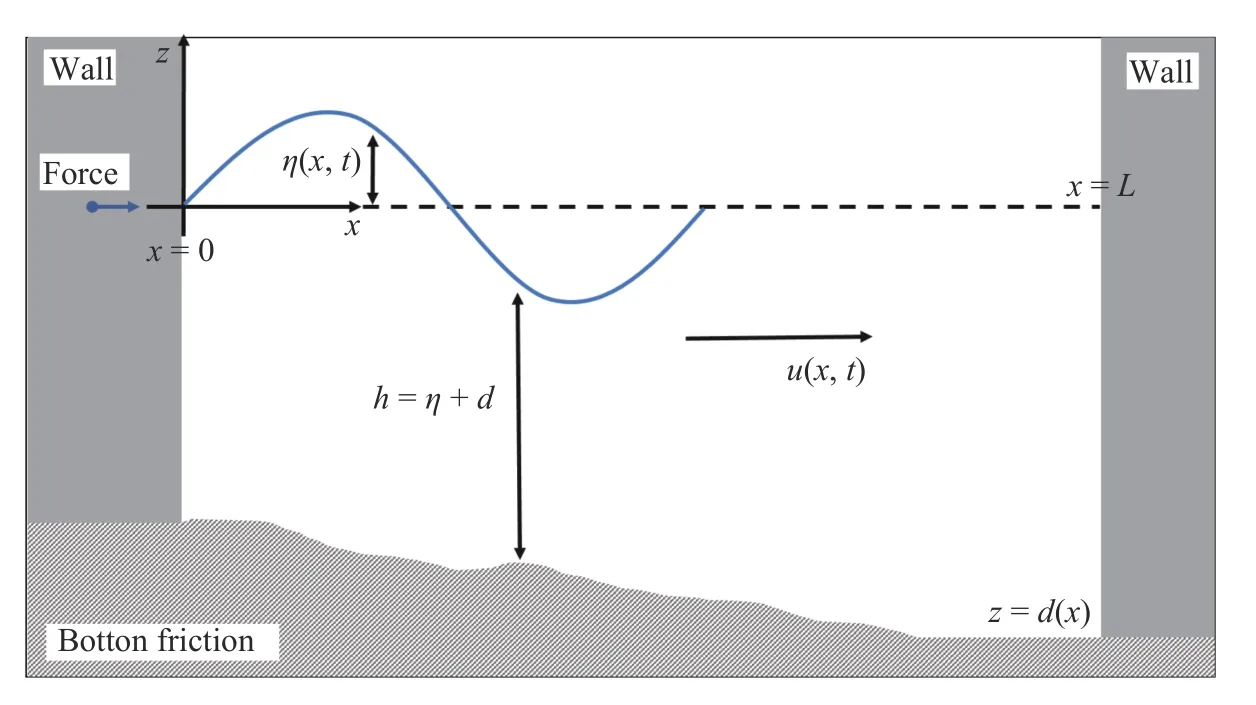
Fig. 1.Modified linear shallow water equations model for wave propagation in a closed basin with bottom friction

The mathematical model that we use in this paper is based on the known linear shallow water equations (LSWEs). The governing equations LSWEs are then improved by introducing the friction termCf uto represent the bottom friction. This adjustment is included in the momentum equation, or the second equation of the model [24]. Our model for wave propagation over a topography with bottom friction may therefore be written as

whereg= 9.81 m/s2is the gravity acceleration andhdepends on the basin's types, which, for this paper, are rectangular,triangular, and parabolic closed basin. The total water depth for each basin is:

in whichh1is the maximum value of the total water depth.Equations (1) and (2)will then be solved analytically and numerically for the three closed basin shapes listed above.We will derive the analytical solution for Eqs. (1) and (2) to obtain the natural resonant frequency of a wave as it propagates in closed basins of different shapes. In order to achieve this, We begin by taking the partial derivative of Eq. (1) with respect totand substituting Eqs. (1) and (2) into the result. What we have now is the equation

In this case, we assume that the wave generated into the basin is monochromatic, then we can write the wave elevationη(x,t)and wave velocityu(x,t) as

withF(x) andG(x) being unknown functions ofx. To determine the natural resonant frequency (ω) of a wave over a rough topography, we need to solve the differential Eq. (3) and obtain the solution ofF(x) and its derivatives with respect tox. Below are the derivation for each case of closed basin.

(1) Closed rectangular basin with depthh(x)=h1in domain[0,L].

To obtain the solution forF(x) in the first case, we substitute Eq. (4) andh(x)=h1into Eq. (3). We also know that e−iωt=0,which allows us to derive

with hard-wall boundary condition at both ends of the basin(considering that the basin is closed), which are mathematically written as

Using the method of characteristics, we obtain a solution for this second-order partial differential equation. The solution in question is

with the wave numberk,k2=(ω2+iωC f)/(g h1)as its dispersion pattern, wherek∈C andω∈R. Using the instability analysis procedure that can be found in Ref. [25], it is shown that the dispersion relation for our governing equations produces no instability, either absolute or convective instability. In this case,the bottom friction coefficientCfplays an important role in restricting the unlimited growth of the wave height, hence, the instability does not exist.

Now that we have the solution ofF(x), we can determine the natural resonant frequency using the boundary conditions for this case. Using the left boundary condition,Fx(0)=0, we obtain

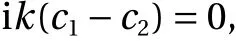
and thusc1=c2. The other boundary condition,Fx(L)=0, gives us

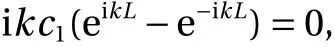
in whichk L=nπwithn=0,1,.... Letn=1to obtain the fundamental value of the natural resonant frequency, in which we have

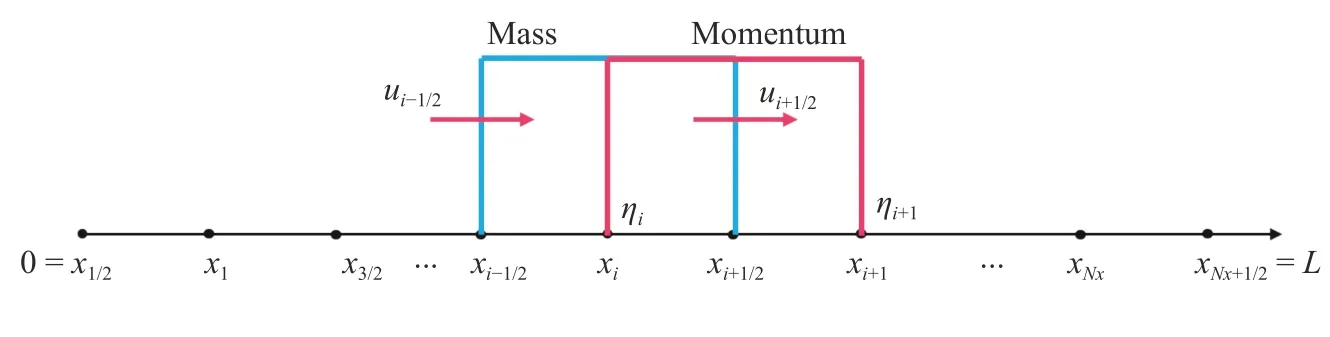
Fig. 2.Illustration of staggered grid discretization

Therefore, we can say that

Now we solve this equation using the quadratic formula. As with the previous cases, we know thatω≥0. So we can defineω,the resonant frequency of a wave propagating in a closed semiparabolic basin with friction, as

withA=|−iC f/2|andω02=8h1/L2as the squared frequency of the wave over a friction-less closed parabolic basin.Notice that from the derivation of each scenario, we obtained the same result of the fundamental natural resonant frequency that is the function of the friction coefficientCfand the friction-less natural resonant frequencyω0, withω0being different, depending on the form of each basin. From this, we may assume that the same result would be most probable to be obtained for any form of bottom topography.

We will develop two computational schemes to approximate the linear model discussed and the non-linear model that will be explained briefly later in this part. The schemes will be constructed using the Finite Volume Method on a Staggered Grid. Now,consider [0 ,L] as our spatial domain which will be discretized using the staggered grid into0=x1/2,x1,x3/2,...,x N x,x N x+1/2=L.The illustration of the discretization method is displayed in Fig. 2.

For the first numerical scheme, which will be used to simulate the linear model, we compute the mass conservation Eq. (1)in every cell centered atxi+1, which is seen as the blue cell in the illustration, while in every red cell centered atxi+1/2, we calculate the momentum Eq. (2) withi=0,1,2,...,N x. In the case of staggered grid discretization method, the wave elevation (η) and the total water depthhwill only have values at full-grid pointsxi+1, whereas the horizontal velocity (u) only has value at halfgrid pointsxi+1/2. The approximations of Eqs. (1) and (2), using the finite volume method, can now be written as

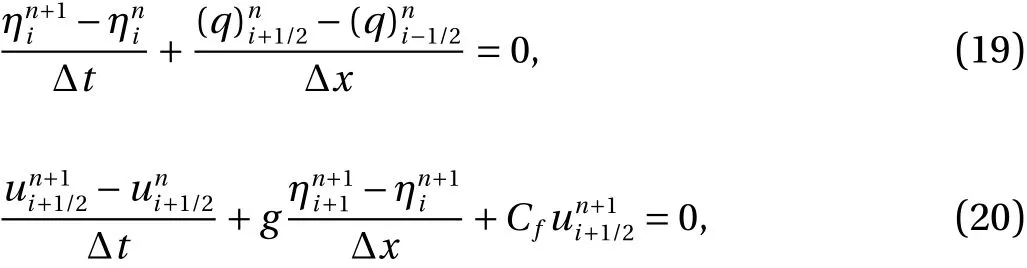
whereq=h uis the wave flux with its discrete formqi+1/2=∗h i+1/2ui+1/2. The term∗hi+1/2is a value that we do not have yet, because the expressionhonly has values at full-grid points. Hence, we have to estimate∗husing another scheme. In this circumstance, a simple approach, which is the first order upwind method, may be used to approximate those values, read as follows

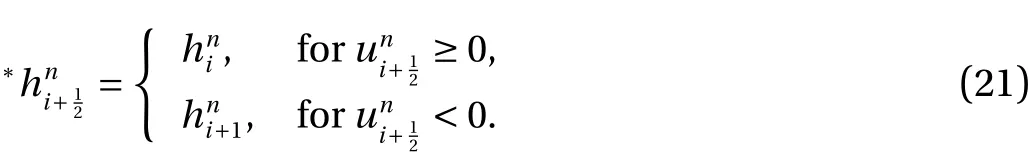
For an additional note, we have the friction elementCf uin the momentum equation implicitly approximated bywhich is used to preserve the stability condition such that the more limited condition can be avoided. Consequently, we can have the same stability condition for our first numerical scheme as that applied to friction-less LSWEs model which isThe stability condition is determined using the Von Neumann stability analysis.

Now, for the second computational scheme which will be used to approximate the non-linear model of wave propagation inside a closed basin, we use the exact same scheme as the first one, but include a non-linear termuu xin the momentum Eq.(20). The termuu x, which can be rewritten as

can be approximated by

The value of the barred variables are calculated from

while the term∗uis approximated using a similar method to estimate∗hwhich is the first-order upwind method, written as

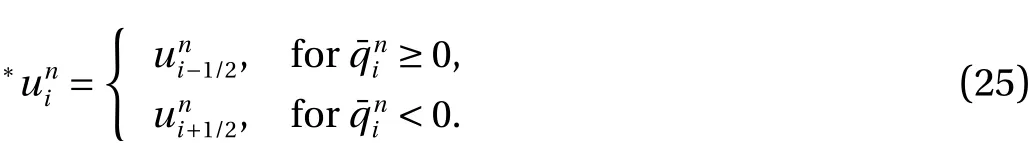
In conclusion, our first numerical scheme Eqs. (19) and (20)that are completed by Eq. (21) will be used to simulate the linear model of wave propagation in a closed basin with rough topography. In addition, the second scheme which consists of Eqs.(19)–(25) withCf= 0 will be used to simulate the non-linear model to study the effect of waves non-linearity on limiting its height growth.

The linear and non-linear numerical scheme proposed in the previous part will be used to simulate the effect of bottom friction and non-linearity on preventing the waves height unlimited growth, respectively. The results from the linear numerical simulations will be compared to the analytical solutions to study the effectiveness of our numerical scheme. The non-linear computational simulations will be used to investigate how non-linearity affects wave height growth compared to bottom friction.

Here, the numerical scheme consists of Eqs.(19)–(21), is used to model the resonance phenomenon in a rectangular, triangular, and parabolic closed basin. The computed values for the natural resonant period of each basin will be acquired from the simulations, which will then be compared with the analytical solutions. In addition, numerous simulations involving bottom friction will be performed to examine the effects of bottom friction on resonance phenomena. How the bottom friction affects the resonance in each type of basin can be seen by finding the minimum natural non-resonance period as well as changes in the growth rate when the friction coefficient is included. This relation between the friction coefficient and resonance phenomenon will be explored later.Now, in order to verify our computational model, we must carry out several simulations and compare the numerical resonant period with the theoretical solutions. First, for computation,we consider a spatial domain of [0 m, 20 m] with the observation time ofT=100 s. We define ∆x=0.1 m as the length of the partition, andas the time step, based on the stability condition. The total water depth of the closed basins orh(x)are following the ones that are used in the analytical derivation section with the maximum depth is set to beh1=10 m. The wave that is generated within the closed basin has an initial amplitude ofAi=1 m. The boundary conditions used here are the same as those described, which are hard-wall on both sides of the domain, or mathematically written asu(0,t)=u(L,t)=0.In addition, the initial condition of the water inside the basins is calm or undisturbed. Into the inside of the basin, the wave is generated by giving external forces. In the case of a small artificial basin, such as glass or bowl, an external force can be created by shaking, moving or slightly hitting the object. The numerical resonant periods are obtained by conducting several simulations to find the one period that can cause a resonance. The analytical resonant period is calculated from the solutions ofωwhere the natural resonant period isT1=2π/ω. The comparison between analytical and numerical natural resonant periods is presented in Table 1.

In Table 1, we present the theoretical and computational natural resonant periods orT1for three different friction coefficient valuesCf. The first value isCf=0, which reflects the lack of bottom friction in the basin, whileCf=0.01 is when friction is weakly present, but the resonance is still generated inside the basin. The last value, which isCf=f0is where the wave undergoes a non-resonance state in the basin with bottom friction, but the values off0are different based on the structure of the basin.This non-resonance condition will be discussed later in this section. The errors presented in Table 1 are the average relative error

of each basin for all three distinct values ofCf. The relative error follows the formula ofBased on those errors that are less than 0.4% for all kinds of basin, we may assert that our numerical natural resonant periods are in agreement with the analytical solutions. Therefore,our computational scheme is quite well validated and can be used to further analyze resonance phenomena in a closed basin.Also, notice that by decreasing the friction coefficient of the basin floor, we are marginally reducing the natural resonant period, which naturally affects the resonance phenomena.Moreover,how the changes ofCfphysically affect the resonance phenomena and the wave profile, will be demonstrated in the next simulation.

Using the same parameters, we undertake numerical simulations to study the effect ofCfon changing wave profiles and res-onance phenomena. The simulations are performed using an analyticalT1, which is a function ofCf, as the natural resonance period for each basin. At the very right end of each domain (x=20), we will capture the amplitude of the waves at each time step, so that we can examine how the waves behave during observation. The results for rectangular, triangular, and parabolic basin with differentCfare shown in Figs. 3–5, respectively.

Table 1 Comparison of analytical and numerical natural resonant periods for each type of closed basin.

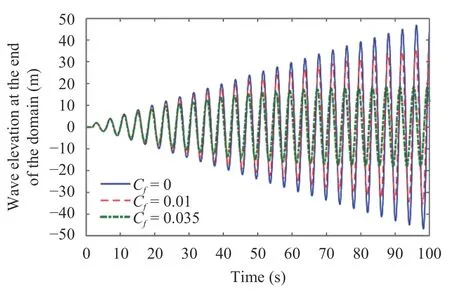
Fig. 3.Simulation results of resonance phenomena in a rectangular closed basin with various C f

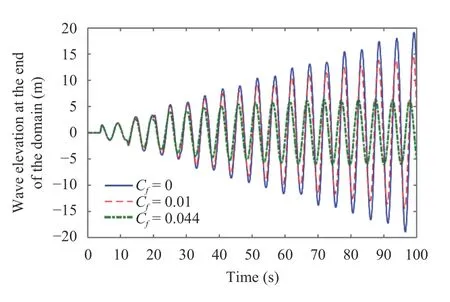
Fig. 4.Simulation results of resonance phenomena in a triangular closed basin with various C f

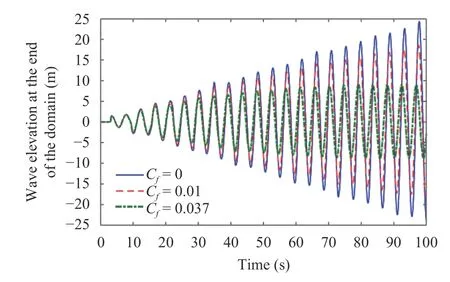
Fig. 5.Simulation results of resonance phenomena in a parabolic closed basin with various C f

Now, from Figs. 3–5, we may study the behavior of the wave in all three types of basin when the values of the bottom friction coefficient are reduced. There are three different values ofCf,with the first one isC f=0,or when the bottom friction is ignored in the model.This friction coefficient contributes to a resonance phenomenon formulation in the basin. In the graphs,resonances are illustrated by the gradual increase of the maximum waves amplitude during the observation time. This behaviour is also found in all basins forCf=0.01. In this case, even though the bottom friction is present, there is still a resonance phenomenon in the basin. In the figures, we can see that the highest amplitudes are always increasing over the time frame,but not as much as when there is no bottom friction at all.

However, this resonance indication will not be able to be tion required for the basin to be in non-resonance situation. As seen in the next case whereCf=f0which is the minimum fricstated before, the value off0is different for each basin. For rectangular basin, the value isf0=0.035, while for triangular, it isf0=0.044andf0=0.037 for parabolic type. Those different values off0are determined numerically by testing the wave profile for differentf0. Resonances are considered to stop occurring when a declining pattern begins to appear at the end of the wave profile. With that indicator, the values off0are found and apparently are different, depend on the shape of the bottom. As can be noticed from the figures, the basin with the smallest to the largestf0can be sorted as rectangular≤parabolic≤triangular.This finding indicates that we will need more friction to stop a resonance from occurring in a triangular type of basin, compared to the other two types, while rectangular need relatively small friction to reach the non-resonance condition. The result also suggests that the bottom friction gives the best outcomes in the rectangular basin but performs badly in the triangular kind.This argument will be supported by the next discussion on changes in wave growth rates whenCfis increased.

In Table 2, we get the information about the growth rate of wave amplitude when resonance is generated in each type ofclosed basin, which is whenCf=0 andCf=0.01, representing a basin without and with bottom friction, respectively. The growth rates presented in the table are obtained from the linear growth rate formula, which can be written asrepresents the wave amplitude at the last crest or peak point showed in Figs. 3–5, whereascrest Idenotes the amplitude of the first crest point. Here,t Fandt Iare the time steps whencrest Fandcrest Icome into view, respectively. In addition, Table 2 also implies that the growth rates are reducing as we increase the value of friction coefficient fromCf=0 toC f=0.01 for each case of basin. Notice that while the rise inCfis the same for all types of basin, the changes in growth rates are different.The growth rate in rectangular basin dropped the most by 5.808%, followed by parabolic and triangular shape which are reduced by 3 .884% and 2 .893%, respectively. From this result,we may argue that the bottom friction affects the resonance phenomenon the most in rectangular basin compared to the triangular and parabolic form. Thus, it requires a lower value ofCf,compared to the other two, to prevent the resonance. On the other side, in order to avoid the resonance effect in the triangular basin, we will need a greaterCf, because the bottom friction impacts the growth rate the least in this sort of basin. Both statements are in line with the finding presented in the previous discussion.

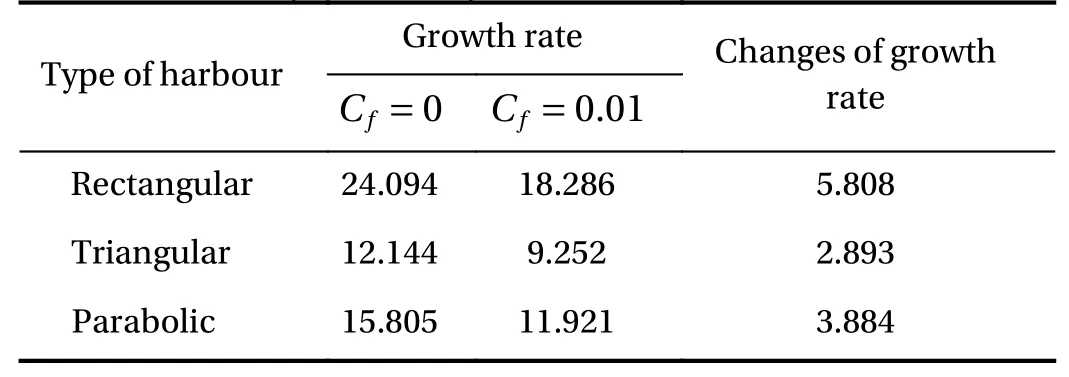
Table 2Growth rates of resonant wave amplitude in each type of closed basin for Cf=0 and Cf=0.01.

Fig. 6.Comparison of the effect of bottom friction and waves nonlinearity of resonance phenomenon

Now, we will study the other factor that can provide some restrictions to resonance phenomenon, that is the non-linearity effect of the wave itself. We use the numerical scheme Eqs.(19)–(25) withCf= 0 to perform the simulations. The results of the simulations will be presented and compared to the results from previous subsection to investigate how different the nonlinearity and bottom friction affecting the resonance. For the computation, we use exactly the same parameters as used in the first subsection, but we set the friction coefficient to beCf=0 to show that there is no friction in the basin, so that we can only study about the non-linearity effect. Similar to the previous one,we capture the maximum amplitude of the wave at the end of the domain each time step to study the characteristics of the resonance phenomenon in this scenario. We will only present the results for rectangular basin as a representation of the comparisons between bottom friction and non-linearity effect on resonance. Figure 6 shows the result of the comparison.

Notice that in Fig. 6, the red dash line which represents the non-linearity effect on wave height is behaving very differently compared to the bottom friction effect. In the non-linear model,the maximum amplitude at the end of the domain is increasing,while the wave height remains steady. This also means that the water surface is also increasing, following the wave amplitude.This could be unfortunate for the coastal area, because if this keeps happening, then flood or other disasters cannot be avoided. Moreover, even though at first, the wave amplitude affected only by the non-linearity is smaller than the one affected by bottom friction, at the end of the observation, it can be seen that the non-linear amplitude keeps rising, while the one with bottom friction is reducing and then constant. This indicates that only non-linearity effect of the wave is not sufficient to prevent the resonance. Instead, we need external factor, such as friction to restrict the wave growth effectively.

In this paper, a modified linear shallow water equations model is used to simulate a resonance phenomenon in a closed basin with bottom friction. The modification is made by including a friction term in the momentum equation as a representation of the existence of bottom friction. Three different types of basin, which are rectangular, triangular, and parabolic basin, are studied. Then, the model is solved analytically and numerically to obtain the natural resonant period, which is the period that can induce a resonance. Analytical derivation reveals that, for all three basin types, the natural resonant period for the bottom friction situation has the exact same formula, which is a function of the non-friction natural resonant period of the corresponding basin as well as the friction coefficient. From this, we may claim that the same function could also be applied to determine the natural resonant period of other types of basin with bottom friction, outside the three that we have discussed here.From the function, we noted that the friction natural resonant period decreases as the friction coefficient increases. Moreover,a computational scheme is formulated to solved the model using the finite volume method on a staggered grid. To verify the numerical method, the findings are compared to the theoretical solutions, which resulted in a rather strong agreement with an average error of less than 0 .4%. In addition, the effects of the increase in friction coefficient on the behaviour of the resonant waves in each basin are studied. From the observation, the bottom friction is the most effective in the rectangular type of basin,resulting in only a low friction coefficient needed to stop the resonance. In contrast, in the triangular basin, the value ofCfrequired to avoid resonance is greater since the bottom friction is the least powerful in this sort of water body. Furthermore, a nonlinear numerical scheme is also formulated to investigate the different effect caused by bottom friction and wave non-linearity on wave height growth by including a non-linear term into the original model. This simulation shows that only non-linearity is not enough to avoid resonance, we also need external forces,such as friction, to stop the resonance, even reduce the wave amplitude.

Acknowledgement

This work was supported by the ITB Research Grant.