Efficient model for the elastic load of film-substrate system involving imperfect interface effects
2020-12-13WenwangWuHuainYuRuiXueTianZhaoRanTaoHaitaoLiaoZhongdongJi
Wenwang Wu, Huain Yu, Rui Xue, Tian Zhao, Ran Tao,*, Haitao Liao,*, Zhongdong Ji
a School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China b Institute of Advanced Structure Technology, Beijing Institute of Technology, Beijing 100081,China
c Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
Keywords:Film-substrate Imperfect interface Elastic field
ABSTRACT In this paper, an efficient calculation method based on discrete Fourier transformation is developed for evaluating elastic load induced elastic deformation fields of film-substrate system.Making use of 2D discrete Fourier transformation, the elastic fields induced by Hertz load is harvested in frequency domain, and the displacement and stress fields across the interface are enforced to satisfy the elasticity conditions for each Fourier modes.Given arbitrary distributed stress field at free surface plane of the three types of film-substrate systems,unique resultant elastic field within the can be harvested. Hertz load of half space, elastic film on elastic substrate,elastic film on rigid substrate system and elastic film-substrate system with three types of imperfect interface models are investigated:(1) the spring-like imperfect interface model which can be described as:(2) the dislocation-like interface model, where interface displacement and stress components relation can be described as:(3) the force-like interface model, where interface displacement and stress components relation can be described as:andrespectively. Finally, several simulation examples are performed for verification of the reliability and efficiency of the proposed semi-analytical methods.©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Mechanical contact induced structural failure problems are of critical important in many industrial systems, such as: train wheel-rail system, transmission, cylindrical and planetary gearing, bearing components, and coating systems. These industrial components and systems have to endure various types of external mechanical, thermal loadings, harsh physical and chemical coupled environments during their service lifetime, and classic film-substrate design strategies are widely employed for improving their comprehensive mechanical performances. As to the interface properties of film-substrate system, bimaterial system and multi-layered structures, classical perfect bonding interface model is employed for studying the mechanical behaviors of these systems under external loading, where the interface traction stress and displacement components are continuous across the material interface. Although the perfect bonding interface model is convenient for theoretical understanding the mechanical behaviors of these integrated systems, it is not precisely valid for industrial structures in service. There are various types of imperfect mechanical interfaces during the service lifetime of film-substrate system, and investigation of the mechanical behaviors of film-substrate systems under external boundary load conditions is important for understanding the durability, reliability of these structural components and systems. In reality, perfect interface mechanical continuity is inadequate for precisely description of interface damage (e.g. de-bonding, sliding and/or cracking across an interface), since it is well-known that imperfect bonding along a material interface can significantly influence its mechanical and thermal properties [1]. Regarding to the relation between interface displacement and traction stress components across the imperfect interface, four types of classic interface models are proposed for describing the interface physical properties, namely: the classical perfect bonding model, the frictionless imperfect interface model, the dislocation-like imperfect interface model, and the force-like imperfect interface model [2–12].
Exact elastic fields analytical solutions of layer-substrate system are proposed by Chen [13]. Mixed boundary value problem in a multilayer medium is analyzed based upon classical elasticity theory, and comparison with classic Boussinesq problem is performed for verification [14]. Making use of generalized self consistent scheme (GSCS) model, the thermoelastic properties of unidirectional fiber composites with imperfect interface conditions are investigated, and linear relations between interface tractions and displacement jumps are assumed [15]. Linear relation between displacement differences and traction stress across the interface are employed for describing the imperfect interface between fibers and matrix, and the initiation, propagation and arrest of interface cracks of fiber-reinforced composite are analyzed based on a criterion of critical strain energy density[16]. The Mori–Tanaka estimate and its modification are used to evaluate the effective modulus of composites with imperfect interface described by linear spring-layer of vanishing thickness[17]. Making use of conjugate gradient method and fast Fourier transform algorithm, the elastic field and thermal field of two heterogeneous bodies subjected to both contact and frictional heat loads are investigated [18]. Through combining conjugate gradient method and fast Fourier transform methods, a novel method for analyzing the fretting contacts of multilayered or functionally graded materials is proposed, where the frictional contact equations are divided into contact pressure and shear tractions [19]. Similarly, through combining conjugate gradient method (CGM) and the discrete convolution (DC)–fast Fourier transform (FFT) algorithm, efficient semi-analytical solutions are derived for analyzing the resultant electric/magnetic potentials and subsurface stress fields due to 3D frictional magnetoelectroelastic (MEE) contact of two multiferroic bodies [20].
Based on the derivation explicit integral kernels for the eigenstrain-induced elastic fields in bi-materials, elastic fields induced by eigenstrains within bimaterials with perfectly bonded and frictionless interfacial conditions are derived [21]. Making use of Chen–Yao's surface elastic theory, size-dependent semianalytical model (SAM) is proposed for solving the rigid frictionless cylindrical indentation contact of a functionally graded elastic film [22]. Closed-form solutions for the eigenstrain-induced elastic fields in bimaterials with coupled dislocation-like and force-like imperfect interface models are derived [23]. Making use of CGM and FFT, an SAM is developed for treating the surface electric/magnetic potentials and subsurface stresses induced by the frictional MEE surface contact of a multiferroic thin film [24]. Elastic fields caused by pressure and shear tractions applied on the surface of such a layer substrate system are derived based on Papkovich–Neuber potentials, where dislocationlike, force-like, spring-like, and frictionless interfacial conditions are considered [25, 26]. Elastic deformation in bimaterials due to an inclusion with dilatational misfit strain is studied, and dislocation-like interface model is proposed for theoretical explanation [27]. Based on the multi-level multi-summation and conjugate gradient techniques, surface deflections and subsurface stresses for real rough surfaces under contact loading are solved with a single-loop alternative numerical method [28]. A thermo-mechanical model of point contact is established for studying the influence of the size, position and interval of inhomogeneities on temperature field of inhomogeneous materials under frictional heating [29]. Based on the closed-form solution of frequency response functions, coupled thermo-mechanical contact problem of a multilayered material is solved, and resultant heat flux, temperature, displacement and stresses at each interface can be harvested [30]. Making use of closed-form frequency response functions, different kinds of heat flux in multilayered coatings are studied and the resultant thermal fields are derived through thermal conduction equation [31]. Elastic fields of dislocations within isotropic, anisotropic half space,thin film, film-substrate and multilayers systems based on discrete Fourier transformation analysis, where perfect-bounding,linear spring, dislocation-like and force-like interface models are considered, respectively [32–39].
In this paper, an efficient calculation method based on discrete Fourier transformation is developed for evaluating the elastic deformation field of half space, elastic film on elastic substrate, and elastic film on rigid substrate system under known elastic boundary loading conditions. Firstly, the boundary loading is converted to the sum of 2D discrete series through discrete fast Fourier transformation. Then, the elastic fields induced by elastic boundary load is harvested in frequency domain, and the displacement and stress fields continuity are remained for perfectly bounded film substrate system. Given arbitrary distributed boundary stress field at free surface plane of half space and film-substrate system, unique resultant elastic field within the system can be harvested. Afterwards, effects of interface discontinuity are studied, and three types of film-substrate system with imperfect interface models are specially focused: (1)the spring-like imperfect interface model which can be described as:KNσzz; (2) the dislocation-like interface model, where interface displacement and stress components relation can be described as:(3) the force-like interface model, where interface displacement and stress components relation can be described as:andrespectively. Finally, several simulation examples are performed for verifying the reliability and efficiency of the proposed semi-analytical methods.
Isotropic film-substrate system with perfectly bounded interface conditions is considered, where boundary elastic load is applied on the top surface plane of the film-substrate system, and the film-substrate interface displacement and traction stress components related to film normal direction should be continuous. The mechanical properties of film and substrate materials is isotropic, with modulus and Poisson ratio(λf,µf,vf) and(λs,µs,vs) for the film and substrate, respectively.Based on linear superposition principle of linear elastic problem, the filmsubstrate system can be divided into two coupled solid regions:thin film and perfectly bounded substrate half space,where the thickness of thin film is 2h,and−h≤zf≤his employed for describing the thin film. Meanwhile,zs≤0 is employed for describing the substrate, withzs=0 for the film-substrate interface.The upper symbols "f"and"s"stand for the film and substrate, (xf,yf) and(xs,ys) coordinates are employed for describing the in-plane of the film and substrate, respectively. The coordinate origins(xf,yf,zf) for the thin film and (xs,ys,zs) for the substrate are situated at the center of the thin film and the center of the film-substrate interface plane, respectively. As(xf,yf)and (xs,ys) are identical, they will be written as (x,y) in the following. As shown in Fig. 1, the boundary loadis applied on the top plane of the thin film, interface displacement and stress components across film-substrate system should satisfy the following elastic field continuity requirements.
(1) Traction stress on top of thin film induced by boundary elastic load should be identical to the resultant elastic stress components within the film-substrate system:

(2) Resultant elastic displacement and traction stress components across the interface planes of the film-substrate system should be continuous:

Normal elastic Hertz load is employed for simulating the elastic deformation of perfectly bounding film-substrate system,the stress distribution in the Hertz load region can be expressed as a function of distance from the center of the Hertz load area[18–20]:
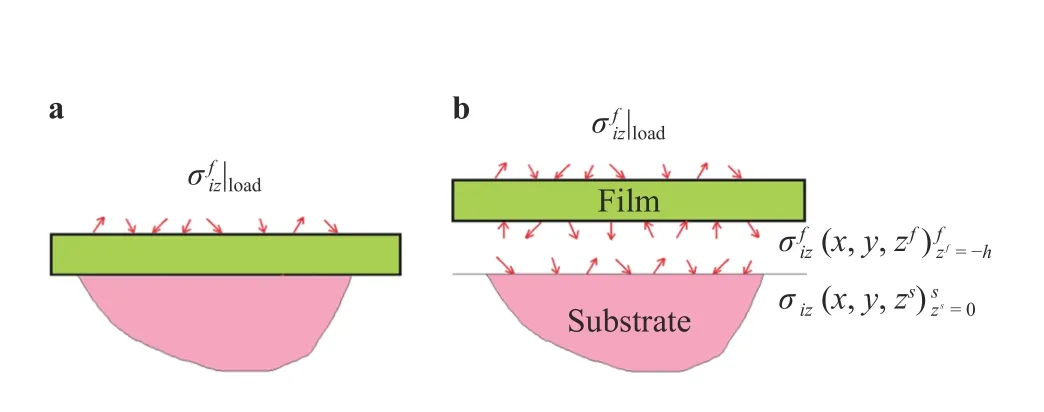
Fig. 1.Decomposition of film-substrate system based on linear superposition principle. a Elastic load isapplied onthe top surface planeof the film, andfree traction boundaryconditionshould be satisfiedonthe topsurfaceplaneofthefilm-substratesystem.bElasticloadstress ?will induceinterfacetractionstress?onthebottomsurfaceof thin film, and?on the topsurfaceof substrate,continuous interface displacement and interface traction stress are generated across the film-substrate interface plane.

wherer2=x2+y2,ais the( Her)tz load patch radius, the maximum pressureP0=3P/2πa2is the stress amplitude of the normal contact stress field.
Making use of 2D discrete Fourier transformation, the boundary Hertz loadq(r) induced traction stress field on the top plane of the film-substrate system can be written in the form of Fourier series:
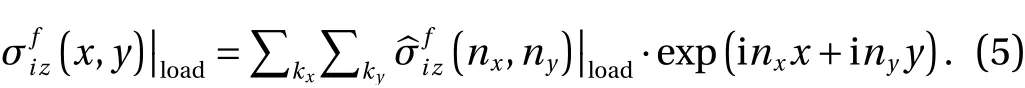
Numerical solutions of Eq. (5) for are considered in thexandydirections with periodic lengthsLxandLy. The wave number is set to benx=2πkx/Lxandny=2πky/Ly, wherekx=ky=0,±1,±2,....
As there is no internal force source and sink, the stress equilibrium equation of the substrate half space can be written as:
The boundary Hertz elastic load on the top of the film-substrate system will induce stress field within the film-substrate system, resulting in continuous interface traction stress fieldsacross the film-substrate interface plane in Cartesian coordinate, which will further generate stress fields within substrate half space medium. Making use of the mathematical completeness of Fourier transformation, the resultant interface elastic field can be written as the sum of Fourier series with unknown Fourier coefficients. The following interface traction stress induced displacement fields are proposed as the solution to Eq.(6), and can be written as:

Due to the completeness of the Fourier transformation, discrete Fourier coefficient components for certainmode can be written as:

Thus, the resultant displacement field within substrate half






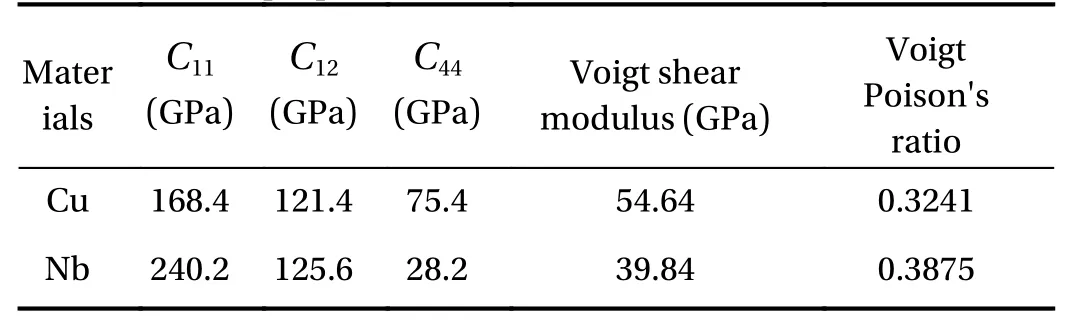
Table 1Elastic properties of Cu and Nb
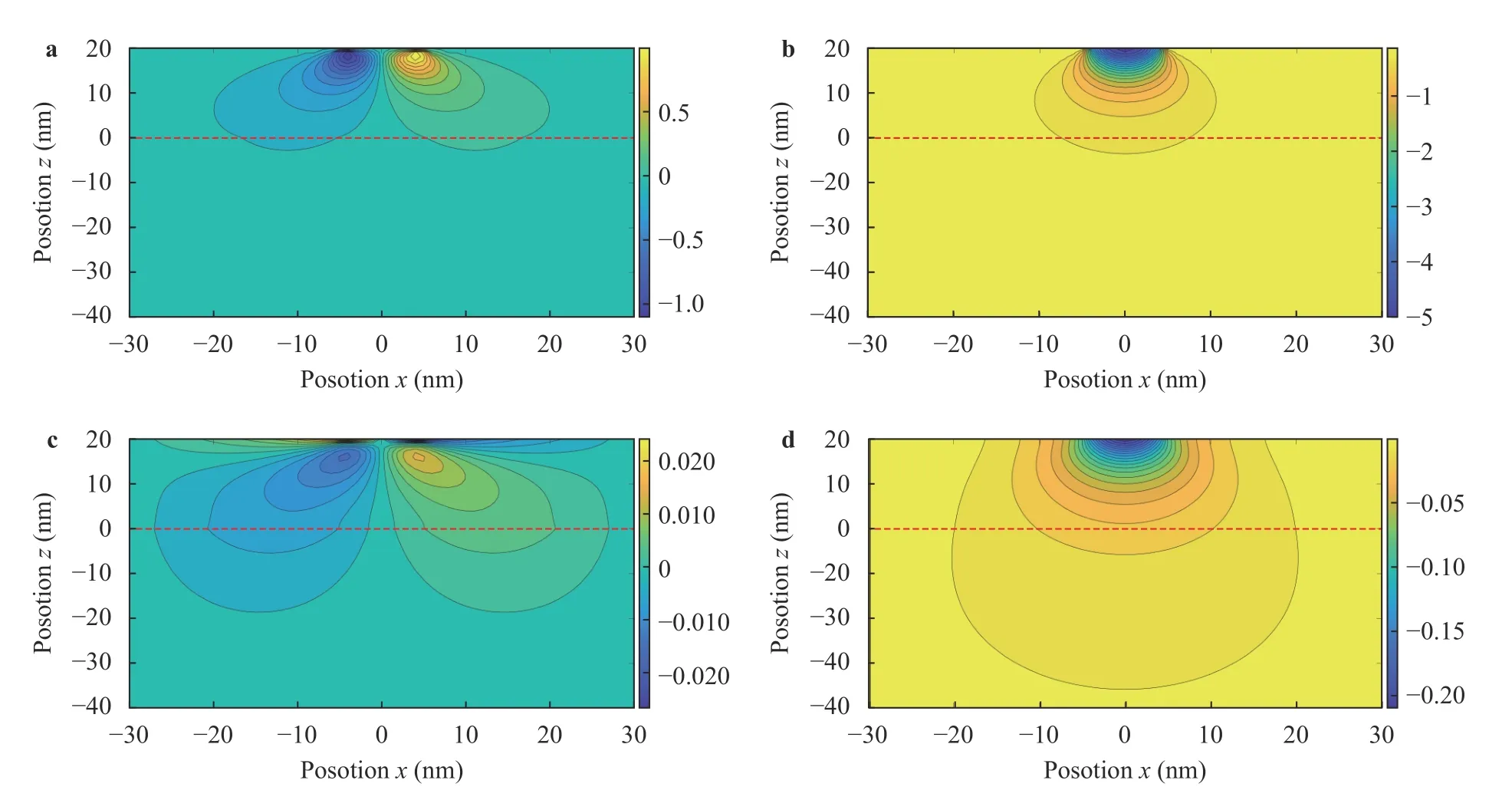
Fig. 3.Resultant stress (unit: GPa) of elastic film-substrate system under Hertz load: and resultant displacement (unit: nm): within film-substrate system.
Fig. 2.Res ultant stress (unit: GPa) of isotropic half space under normal Hertz load: aTx z, bTz zand resultant displacement (unit: nm)withinhalf spac constant for describing the interface imperfection. The periodic Fourier transformation wave number iskx=k y=30. The produced stress fields under normal traction Hertz load are: Fig. 7a forσx z, Fig. 7b forσz z, Fig. 7c foruxand Fig. 7d foru z, respectively. Comparisons of interface traction and displacement profiles alongxdirection in thexzplane (y=0) are shown in Fig. 8.
Hertz load cting on top surface plane of isotropic elastic filmsubstrate system with imperfect dislocation-like interface model is simulated, as described by Eq. (4), where the contact radiusa=5nm, and Hertz stress amplitudeP0=5 GPa. The material of thin film is Cu and the substrate is Nb, with their Voigt isotropic modulus shown in Table 1. The stress field within the cross-section of film-substrate system is plotted with physical scale alongxdirectionLx=100 nm and physical scale alongzdirectionz0=40 nm, including 10 nm thin film and 30 nm substrate along z direction. The dislocation-like interface related matrixesKu=DIA[0.5 0.5 0.5] are set as constant for describing the interface imperfection. The periodic Fourier transformation wave number isk x=k y=30. The produced stress fields under normal traction Hertz load are: Fig. 9a forσx z, Fig.9b forσz z, Fig. 9c foruxand Fig. 9d foruz, respectively. Comparisons of interface traction and displacement profiles alongxdirection in thexzplane (y=0) are shown in Fig. 10.
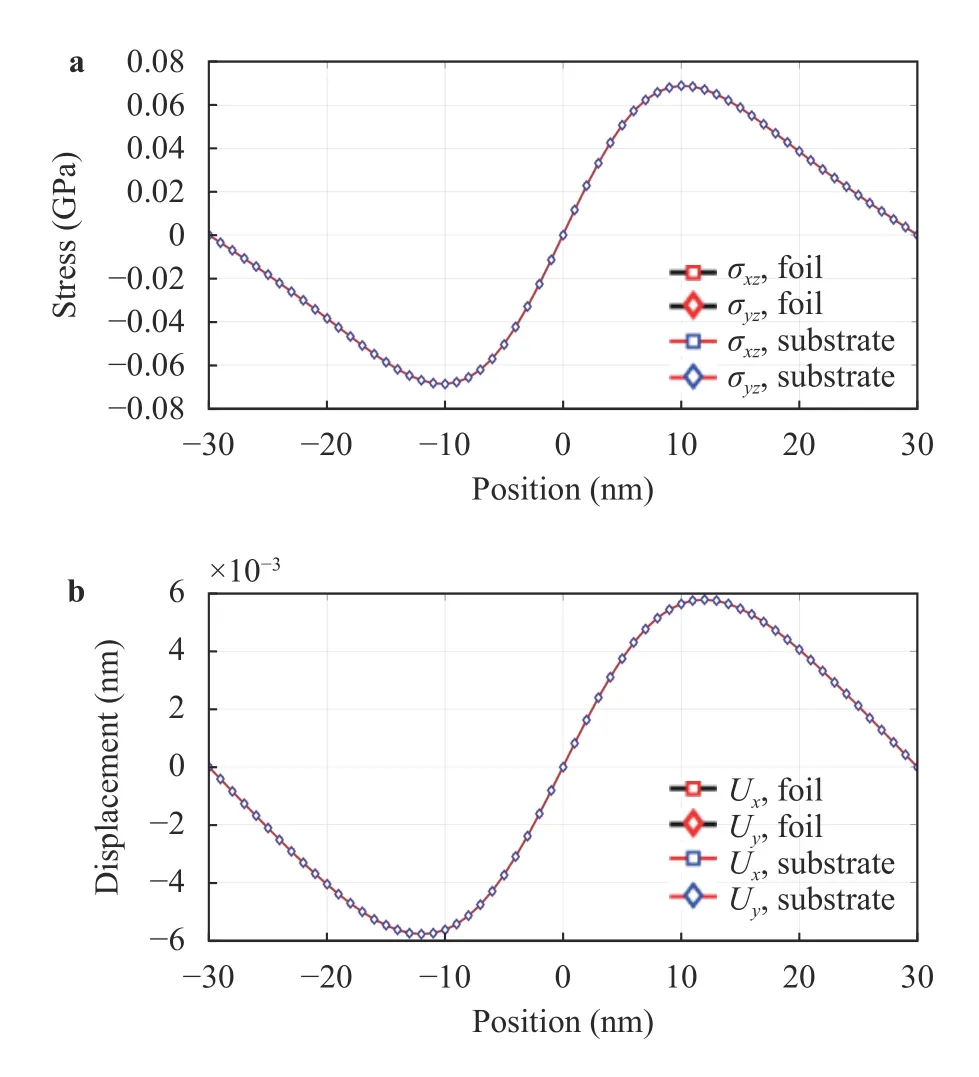
Fig. 4.Comparisons of Hertz load induced interface elastic profiles within elastic film-substrate system: a stress and b displacement.
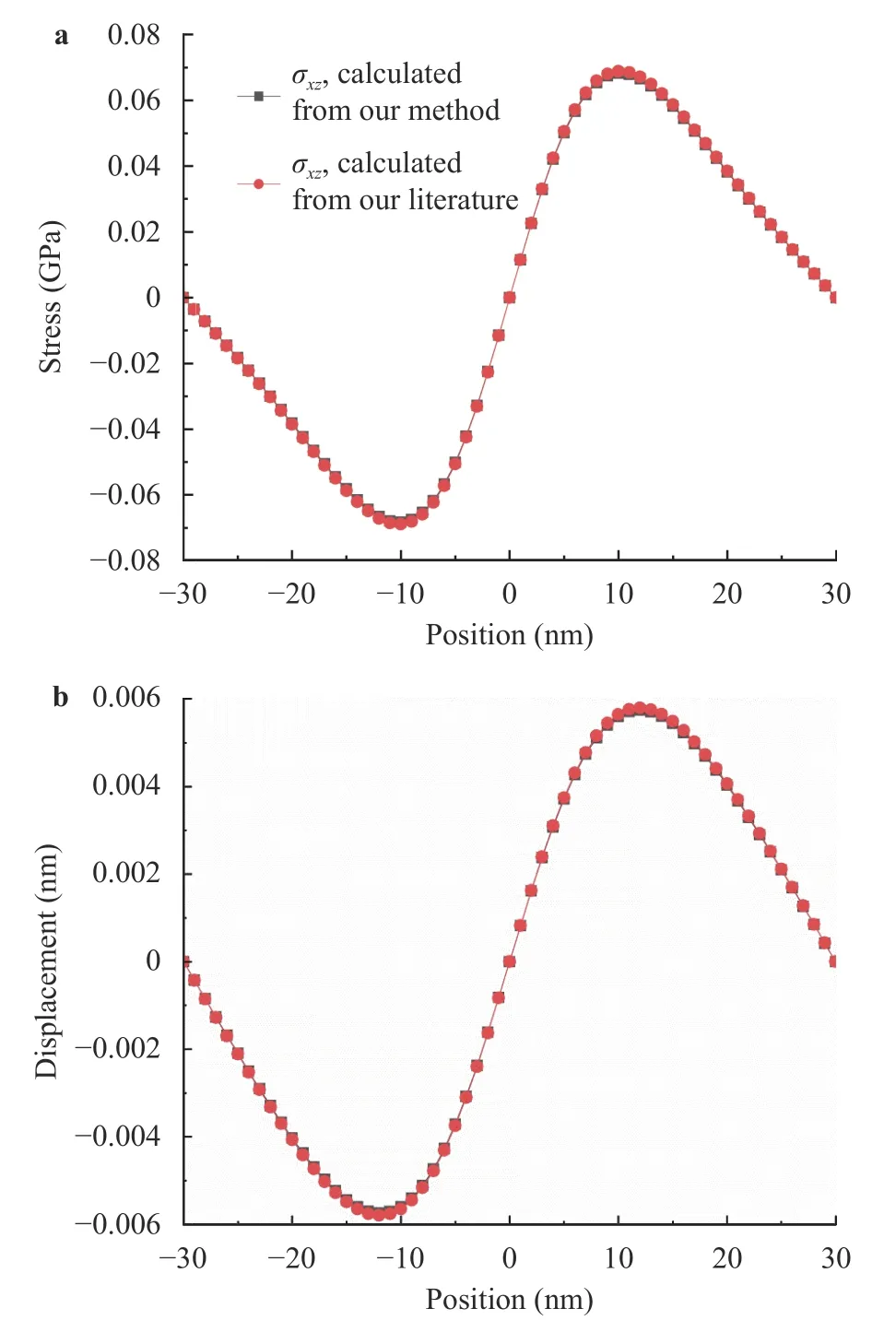
Fig. 5.Verification of our methods with classic method in Ref. [42]for film-substrate system under Hertz load,interface elastic profiles within elastic film-substrate system: a stress and b displacement.
Fig. 6.Resultant stress (unit:GPa)of thin film within elastic film rigid substrate system under normal Hertz load: and resultant displacement (unit: nm): within elastic film space.

Fig. 7. Resultant stress (unit: GPa) of elastic film-substrate system with linear spring-like interface under normal Hertz load: and resultant displacement (unit: nm): within thin film-substrate space.

Fig. 8.Comparisons of Hertz load induced interface elastic profiles within elastic film-substrate systemwith linear-spring interface: a stress and b displacement.
Hertz load acting on top surface plane of isotropic elastic film-substrate system with imperfect force-like interface model is simulated, as described by Eq. (4), where the contact radiusa=5nm, and Hertz stress amplitudeP0=5 GPa. The material of thin film is Cu and the substrate is Nb, with their Voigt isotropic modulus shown in Table 1. The stress field within the cross-section of film-substrate system is plotted with physical scale alongxdirectionLx=100 nm and physical scale alongzdirectionz0=40 nm, including 10 nm thin film and 30 nm substrate along z direction. The force-like interface related matrixesK t=DIA[0.5 0.5 0.5]are set as constant for describing the interface imperfection. The periodic Fourier transformation wave number is:kx=k y=30. The produced stress fields under normal traction Hertz load are: Fig. 11a forσx z, Fig. 11b forσz z,Fig. 11c foruxand Fig. 11d foru z, respectively. Comparisons of interface traction and displacement profiles alongxdirection in thexzplane (y=0) are shown in Fig. 12.
Based on discrete Fourier transformation of elastic boundary load fields, efficient calculation methods for analyzing the deformation fields of half space, film-substrate system and film on rigid substrate systems are explored. Classic Hertz load examples are performed for verification. Afterwards, the method is extend for film-substrate system with imperfect interface continuity cases, and three classic interface models are considered:(1) the spring-like imperfect interface model which can be described as:K Nσz z; (2) the dislocation-like interface model, where interface displacement and stress components relation can be described as:(3) the force-like interface model, where interface displacement and stress components relation can be described as:andrespectively. The proposed novel calcula-tion methods can be further developed for anisotropic film-substrate systems, functionally graded systems.
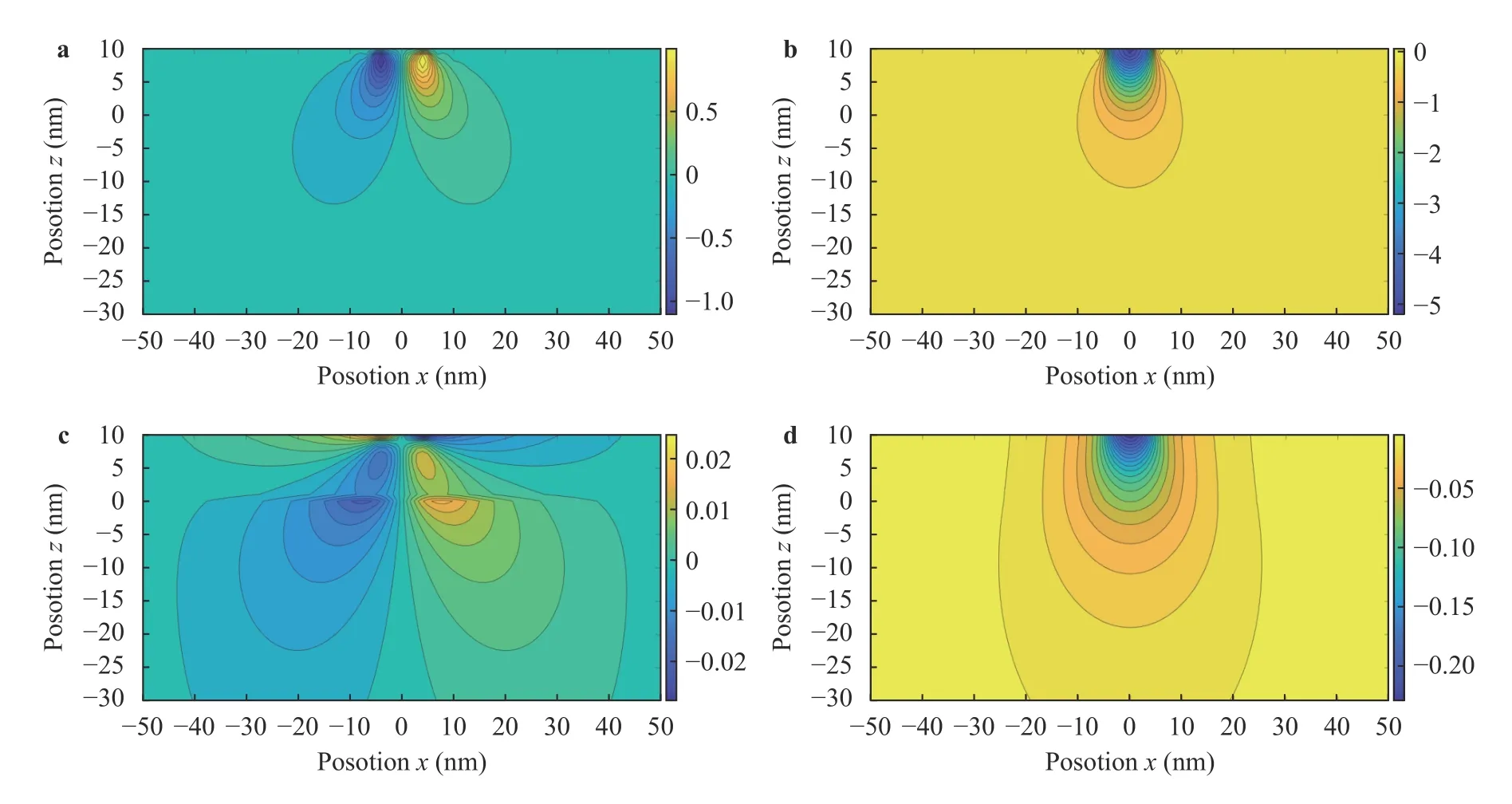
Fig. 9.Resultant stress (unit: GPa) of film-substrate system with dislocation-like interface under normal Hertz load: and resultant displacement (unit: nm): within thin film-substrate space.
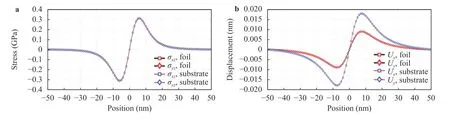
Fig. 10.Comparisons of Hertz load induced interface elastic profiles within film-substrate system with dislocation-like interface: a stress and b displacement.

Fig. 11.Resultant stress (GPa) of film-substrate system with force-like interface under normal Hertz load: and resultant displacement (unit: nm):within thin film-substrate space.
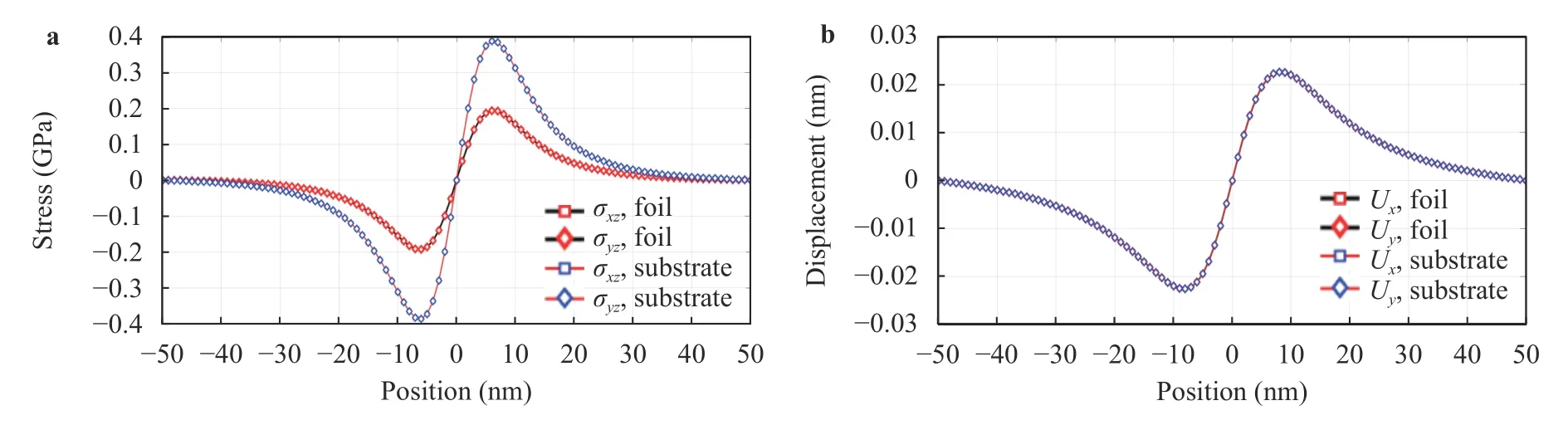
Fig. 12.Comparisons of Hertz load induced interface elastic profiles of elastic film-substrate system with force-like interface: a stress and b displacement.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (Grants 11702023 and 11972081).
Appendix

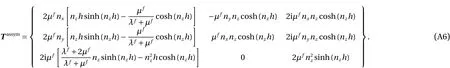
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- A modified Lin equation for the energy balance in isotropic turbulence W.D. McComb*
- Influence of wing flexibility on the aerodynamic performance of a tethered flapping bumblebee
- Interactions of human islet amyloid polypeptide with lipid structure of different curvatures
- Evolution of vortices in the wake of an ARJ21 airplane: Application of the liftdrag model
- Analytical and numerical studies for Seiches in a closed basin with bottom friction
- Ergodic sensitivity analysis of one-dimensional chaotic maps
