Evolution of vortices in the wake of an ARJ21 airplane: Application of the liftdrag model

Jun-Duo Zhng, Qing-Hi Zuo, Meng-D Lin, Wei-Xi Hung,*, Wei-Jun Pn, Gui-Xing Cui

a AML, School of Aerospace Engineering, Tsinghua University, Beijing 100084, China

b Civil Aviation Flight University of China, Sichuan 618307, China

Keywords:Wake vortex Near-ground evolution Large eddy simulation Adaptive mesh Lift-drag model

ABSTRACT Wake separation is crucial to aircraft landing safety and is an important factor in airport operational efficiency.The near-ground evolution characteristics of wake vortices form the foundation of the wake separation system design. In this study, we analysed the near-ground evolution of vortices in the wake of a domestic aircraft ARJ21 initialised by the lift-drag model using large eddy simulations based on an adaptive mesh. Evolution of wake vortices formed by the main wing,flap and horizontal tail was discussed in detail. The horizontal tail vortices are the weakest and dissipate rapidly, whereas the flap vortices are the strongest and induce the tip vortex to merge with them. The horizontal tail and flap of an ARJ21 do not significantly influence the circulation evolution, height change and movement trajectory of the wake vortices. The far-field evolution of wake vortices can therefore be analysed using the conventional wake vortex model.©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

The wake vortex of a leading aircraft during take-off and landing at an airport poses a danger to following aircraft. Wake vortex separation is required to preserve aircraft safety, which strongly affects airport capacity and security [1, 2]. Understanding the evolution and characteristics of aircraft wake vortices is therefore of great significance [3, 4].

Computational fluid dynamics (CFD) has become an effective tool to study wake vortices in recent years. Compared with field measurements, CFD can accurately control the parameters and variables by studying their effects on the evolution of wake vortices. Information is also obtained from the entire flow field,which can be used to quantitatively study wake vortex evolution.Wake vortices can spread over thousands of meters in bodyfixed coordinates, which makes numerical simulations difficult using the present computational resources. Ground coordinates are therefore usually used to simulate wake vortex evolution.Direct numerical simulations (DNS) have been previously performed to investigate the trajectory of two-dimensional wake vortices under different conditions [5–8]. However, long-wave and short-wave instabilities of wake vortices occur under threedimensional (3D) conditions, and thus 3D large eddy simulations (LES) have become a popular approach for numerical studies [1, 9]. Shen et al. [10] and Proctor and Han [11] investigated the 3D instability of wake vortices in a domain with an axial domain length of 2.6b0(whereb0is the initial vortex core distance) using LES. Holzäpfel et al. [12] simulated wake vortices with an axial domain length of 8.5b0to capture the Crow's longwave instability. However, the axial resolution is reduced for computational efficiency and the short-wave instability cannot be detected. Hennemann and Holzäpfel [13] used a computational domain with a long axial length and high axial resolution to recognise both long-wave and short-wave instabilities, but the total grid number reached 60 million with a high computational cost. Misaka et al. [14] conducted higher-resolution wake vortex simulations using a total grid number of 160 million. The high computational cost of using a long axial domain length with high resolution to capture the long-wave and short-wave instabilities therefore poses one of the main challenges of wake vortex simulations.

Traditional wake vortex initialisation models, such as the Burnham–Hallock model [15] and Proctor model [10], have limitations that ignore the effect of the roll-up phase [16]. Misaka et al. [14] and Kolomenskiy and Paoli [17] considered roll-up effects by combining a Reynolds-averaged Navier–Stokes (RANS)approach to the whole aircraft and LES for wake vortex far-field decay. However, the application of this method is far from practical because of the high computational resource requirements.A more practical numerical model is therefore required. Lin et al. [18] proposed a self-adaptive grid method to simulate wake vortices with a high resolution but significantly reduced computational costs. A new lift-drag model for wake vortex initialisation proposed Lin et al. [16] accounts for the effects of a roll-up phase without extra computational cost.

In the present study, we applied the lift-drag model with a self-adaptive grid method to investigate the evolution of vortices in the wake of an ARJ21, which is a new type of regional aircraft with a low-wing and T-shaped horizontal tail [19]. Three lift-drag models were applied for the main wing, flap and horizontal tail to represent the ARJ21 characteristics. In the following, the numerical method and wake vortex initialisation are first introduced. Then the results of the near-ground vortex evolution in the wake of an ARJ21 and the effects of the flap and horizontal tail on the far-field evolution are presented and discussed, before the conclusions are drawn.

The maximum velocity of an airplane wake field is usually less than 30 m/s; the unsteady incompressible Navier–Stokes (NS) equations are therefore considered in the present study.Buoyancy effects caused by the temperature gradient are applied by the Boussinesq approximation. The LES equations are thus obtained by filtering the Boussinesq-approximated N-S equations as follows:

where ui(i = 1, 2, 3) or (u, v, w) denote the velocity components along the coordinates xi(i = 1, 2, 3) or (x, y, z), θ represents the temperature with θ0as the reference temperature, t, p, ρ, ν, κ denote the time, pressure, density, kinematic viscosity and thermal diffusivity, respectively, fidenotes the body force component exerted on the fluid,denotes the subgrid-scale stress andis the subgrid-scale thermal flux. The variables with an overbar represent filtered quantities. In computation, the subgrid-scale stress and subgridscale thermal flux can be expressed as, respectively:

The velocity gradient near the vortex core region is considerably larger than that far from the vortex core. We therefore adopt the flow solver Adaptive Tsinghua Turbulence Laboratory Large Eddy Simulation (ATTLES), which was developed by Lin et al. [18] for atmospheric environment research [21–23]. The major improvement of the ATTLES is a moving Cartesian grid frame that is self-adapted to the flow field, which is developed based on Gnoffo's spring analogy method [24]. In the present self-adaptive algorithm, the grids are assumed to be connected by springs and the stiffness of the springs increases with increasing velocity gradient. The ATTLES also extends the Gnoffo's spring analogy method for steady flows to unsteady flows. In ATTLES,the govern equations are discretised by the finite volume method and solved by the SIMPLE algorithm. A fourth-order Runge–Kutta integration is applied for the time advancement.Details of the numerical method have been described previously [16, 18], and this method has been validated in wake vortex simulations.

We applied the lift-drag model (vortex sheet model) proposed by Lin et al. [18] to initialise wake vortices. Compared with traditional models, the present model can simulate the roll-up phase without increasing the computational cost; thus its effects on the far-field decay can be considered. In the lift-drag model,the force of the aircraft acting on the air is simplified to planar distributed lift and drag. Simulation of the entire aircraft is thus not needed [14] and the roll-up phase and far-field decay of the wake vortices can be simulated together in a single run.

A schematic of the lift-drag model is shown in Fig. 1a, where x, y and z represent the flight direction (or vortex axial direction),spanwise direction and vertical direction, respectively. A vertically downward body force with an elliptical distribution is exerted in a flakiness region with a width equal to the wing span B(where thickness h << B), and length throughout the computational domain in the flight direction.

The distribution of the body force is set to:whereτis the body force duration andΓ0is the initial circulation of the wake vortex, which is expressed as:

whereMis the aircraft mass,gis gravitational acceleration,ρais the air density andVAis the aircraft airspeed. The physical meaning offzis the reactive force acting on the air by the wing.The thickness of the vortex sheethand duration of the body forceτshould be as small as possible to approximate real conditions. In the present study,h= 0.014b0andτ= 0.003b0are used by considering the numerical stability. The process of wake vortex simulation using the lift-drag model is demonstrated in Fig. 1b. A vortex sheet is generated underfzand the vortex sheet then rolls up to form a pair of counter-rotating vortices by selfinduction, which ultimately undergoes far-field decay.

To account for the influence of flight drag, a distributed body forcefxis also added in the flight direction, expressed as:

whereLDis the lift-to-drag ratio, which is set to 12 to simulate the approach of an aircraft based on the study of Keye [25]. The approach speed of an aircraft is relatively low, thus the induced drag is considerably larger than the frictional drag [26]. Equation(8) is therefore used to estimate the aircraft drag.

Fig. 1.Schematic diagram of a wake vortex simulation: a lift-drag model and b flow chart.

Because the main purpose of the present study is to investigate the wake vortex evolution of an ARJ21, a specific model is required to represent the characteristics of this aircraft. The key parameters are shown in Fig. 2. We consider the main wing, flap and horizontal tail, which are assumed to sustain 60%, 50% and 10% of the total lift, respectively. The main wing and horizontal tail are assumed to be elliptical, and the flap is approximated as a rectangular wing. Three lift-drag models are used to represent the three wings, as shown in Fig. 2, where black, blue and red represent the main wing, flap and horizontal tail, respectively.

The initial vortex circulation and separation of the ARJ21 are set toΓ0= 212 m2/s andb0= 21.4 m, and the characteristic velocityw0and characteristic timet0are defined as:

wherew0is the initial vortex descending speed calculated by the Biot–Savart law. For ARJ21,w0= 1.58 m/s andt0= 13.54 s. The Reynolds number defined by the circulation isReΓ=Γ0/ν≈ 1.2 ×107, where the kinematic viscosity of air isν= 1.8 × 10−5m2/s.Rogallo's method [27] is applied to initialise the ambient turbulence. The turbulent velocity in spectral space is:

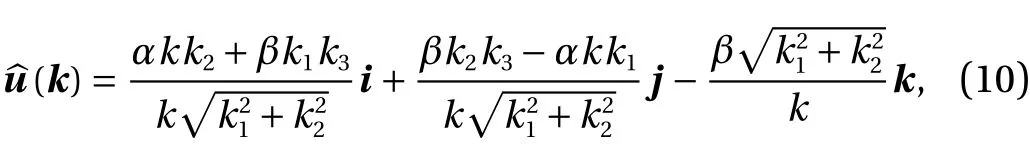
wherekis the wave number vector, andk1,k2andk3are the components ofk.αandβare given as follows to satisfy the kinetic energy spectrum:

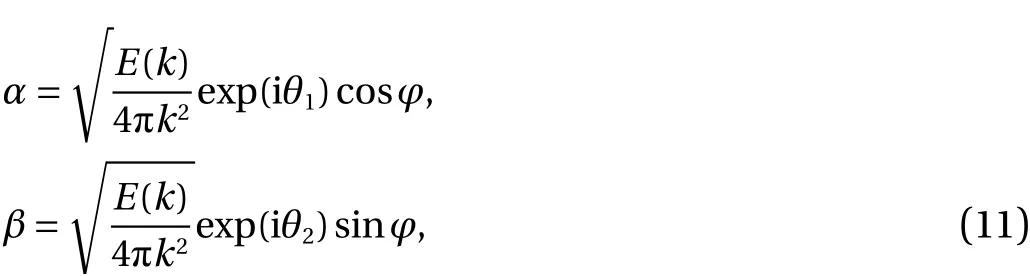
whereθ1,θ2andφare the random numbers uniformly distributed within [0, 2π].E(k) is the prescribed kinetic energy spectrum, which is the von Karman spectrum modified by Bechara et al. [28]:

where the wave number of the energy spectrum peakkpis set to 2π/50 m−1to simulate the near-ground turbulence under neutral conditions andkkol= (ε/ν3)1/4is the Kolmogorov wave number.In this study, the turbulence dissipation rate is set toε= 10−4m2/s3. ThenK0andkpcan be determined by:

Fig. 2.Sketch of the ARJ21 lift-drag model, unit: mm.

After the velocity is obtained from spectral space, the velocity in physical space can be calculated as follows:

In this study, the computational domain is set toLx×Ly×Lz=8.0b0× 7.0b0× 4.2b0with a grid number of 366 × 258 × 125, and the axial domain size is set to 8b0to recognise the potential longwave instability. A uniform grid is applied in the axial direction with a grid size of Δx= 0.022b0(1 m), and an adaptive grid is used in the other two directions. The resolution near the vortex core is set to Δy= Δz= 0.01b0and stretched to 0.07b0away from the vortex, as illustrated in Fig. 3. The time step is fixed to Δt=t0/6800. Periodic boundary conditions are applied in the axial and spanwise directions. No-slip conditions are applied on the bottom boundary, i.e., the ground, while the top boundary adopts zero-gradient conditions.

During the flight of an aircraft, a vortex sheet forms by the circulation shed from the trailing edge of the wing and rolls up to the wake vortices after the near-ground phase or roll-up phase[15]. In the present study, we mainly discuss the results obtained by applying the lift-drag model to represent an ARJ21, as proposed above. The main wing, flap and horizontal tail of an ARJ21 each produce a pair of wake vortices. The horizontal tail vortices (HTVs) are the weakest and opposite to the other two vortex pairs, while the flap vortices (FVs) are the strongest and induce the wing tip vortices (WTVs) to merge with them.

Figures 4–6 illustrate the evolution and roll-up process of the wake vortices along a 3Dλ2iso-surface [29] (with contours of non-axial vorticitytogether with the axial vorticity distribution in a cross section. Att* =t/t0= 0.012, the WTVs, FVs and HTVs form, as shown in Fig. 4a, c. Because the HTVs account for 10% of the negative lift, the rotational direction of the HTVs is contrary with and also much weaker than the WTVs and FVs. Att* = 0.029 (Fig. 4b, d ), the WTVs begin to roll up under induction by the FVs. Rib-like vortices are generated between the FVs as the instability occurs. Att* = 0.059 (Fig. 5a, c),the WTVs continuously roll up and begin to merge with the FVs.The HTVs move downwards induced by the FVs, and the rib-like vortices begin to stretch and roll under the induction. Att* = 0.12(Fig. 5b, d), the WTVs have completely merged with the FVs and become a pair of main vortices. The HTVs move further downwards to the same altitude as the main vortices, and short-wave instability is observed.

Fig. 3.Sectional view of self-adaptive grid.

Fig. 4.Instantaneous structures of the wake vortices: a, b iso-surface of λ2 = −0.5 and c, d distribution of axial vorticity ωx* = ωxt0. In a, c, t* =0.012 and in b, d, t* = 0.029.

Fig. 5.Instantaneous structures of wake vortices:a,b iso-surface of λ2 = −0.5 and c,d distribution of axial vorticity ωx*= ωx t0. In a, c, t* = 0.059 and in b, d,t* =0.12.

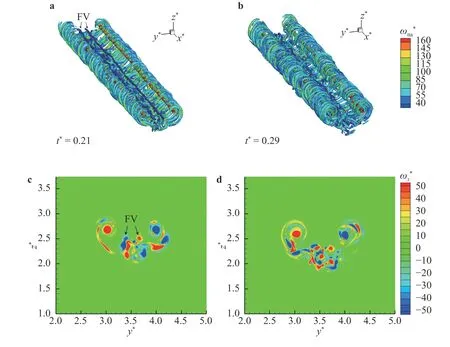
Fig. 6.Instantaneous structures of wake vortices: a, b iso-surface of λ2 = −0.5 and c, d distribution of axial vorticity ωx* = ωx t0. In a, c, t* = 0.21 and in b, d, t* = 0.29.

Att* = 0.21 (Fig. 6a, c), the HTVs begin to encounter rib-like vortices beneath the main vortices. Up tot* = 0.29 (Fig. 6b, d),the HTVs have completely merged with the rib-like vortices and the latter further roll up and become reinforced. Att* = 0.50 (Fig 7a, c), the rolled-up rib-like vortices continuously merge with the main vortices while the vortices beneath the main vortices begin to dissipate under the turbulence effects. The instability also occurs in the main vortices. Up tot* = 0.74, the instability of the main vortices becomes increasingly apparent (Fig. 7b, d) and the roll-up phase is generally completed as the vorticity becomes concentrated in the wake vortex core.

The effect of flight drag is taken into account by the lift-drag model through Eq. (11), and the axial velocity is induced during the roll-up phase. Figure 8 illustrates the evolution of axial velocityu* =u/w0around the wake vortices. Att* = 0.012 (Fig. 8a),the wake vortices are at the initial state and the axial velocity is concentrated in the flakiness region corresponding to the WTVs and FVs, similar to the drag velocity caused by the flight of the aircraft. Att* = 0.026 (Fig. 8b), the axial velocity concentrated in the WTVs moves towards the FV region due to the induction, as seen in Fig 4b, d. Att* = 0.12 (Fig. 8c), the WTV region with high axial velocity merges with that of the FVs. Att* = 0.74 (Fig. 8d),the axial velocity is mainly concentrated in the core of the main vortices as the roll-up phase is completed. The axial velocity distribution resembles that obtained using only the one lift-drag model [16].

After the roll-up of the vortex sheet, the wake vortices develop and ultimately decay in the atmosphere, which is called the far-field phase [15]. The characteristics and effects of the flap and horizontal tail on the far-field evolution is discussed here. In the present study, the far-field decay of the wake vortices is simulated under static wind and neutral ambient atmosphere conditions. The turbulent dissipation rate of the atmosphere is set toε= 1.8 × 10−4m2/s3, and the turbulent integral scale is set to 40 m to simulate the static atmosphere with weak turbulent intensity.Three cases are conducted (Table 1) to study the effects of the flap and horizontal tail on the far-field evolution. Case HT_FLAP uses the three lift-drag models (i.e., main wing, flap and horizontal tail) to represent an ARJ21. Case HT considers two liftdrag models (main wing and horizontal tail), and case CL simplifies the ARJ21 to a single main wing as a comparison case. The ambient atmosphere conditions and total lift of the three cases are identical. The initial height of the wake vortex is set to 2b0=42 m to simulate the final stage of the aircraft approach.

Figures 9–11 compare the effects of the flap and horizontal tail on the wake vortex evolution along a 3Dλ2iso-surface to-gether with contours of non-axial vorticity Att*= 1.0 (Fig. 9), only a pair of WTVs form in case CL because only the main wing is considered. In addition to the WTVs, FVs and HTVs are also generated in case HT_FLAP by the flap and horizontal tail, respectively. The WTVs are deformed and begin to merge with the FVs under induction. Rib-like structures appear between the main vortices in both cases due to the instability, but the rib-like vortices in case CL are more significant than in case HT_FLAP. Figure 10 illustrates the wake structures att*=5.0. Three pairs of vortices merge into a pair of main vortices in case HT_FLAP, and the flow structures are similar in cases CL and HT_FLAP. The rib-like vortices become stronger and further roll up around the main vortices, as compared with those att*= 1.0. Att*= 8.0 (Fig. 11), the rib-like vortices are well developed in both cases and instability occurs in the main vortices.The vorticial structures remain similar in these two cases.

Fig. 7.Instantaneous structures of wake vortices: a, b iso-surface of λ2 = −0.5 and c, d distribution of axial vorticity ωx* = ωxt0. In a, c, t* = 0.50 and in b, d, t* = 0.74.

Fig. 8. Contours of the axial velocity u* = u/w0 at different instances.

Table 1 Set-up of the far-field evolution simulation

Figure 12a shows the time history of circulation for the three cases, in which no major differences are observed. The effects of the flap and horizontal tail on the far-field decay are limited because the HTVs are relatively weak and far from the main vortices, whereas the FVs and WTVs merge as a pair of vortices att*= 0.12. The wake vortex altitude of the three cases is shown in Fig. 12b. Beforet*= 2, the wake vortices descend at a nearly constant speed in all cases and reach the valley at aroundt*= 3. The wake vortices then bounce upwards due to the ground effects and rise to the height ofb0aroundt*= 8. The trajectory of the wake vortex cores is also not affected by the flap and horizontal tail, as shown in Fig. 12c. The lateral distance of the wake vortices remains almost unchanged until they approach the ground(z* < 1), and the distance is then increased under the ground effects due to the bouncing of vortices.

The results of the three cases under the same conditions indicate that the flap and horizontal tail of an ARJ21 have no major effect on the far-field evolution of the wake vortices. The specific ARJ21 model can therefore be replaced by a single lift-drag model with the same weight and size to investigate the features of the wake vortex decay. The ARJ21 wake vortex separation can also serve as a reference for other aircraft of similar weight and size.

In summary, a lift-drag model was applied to represent the ARJ21 aircraft, and ATTLES was used to simulate the evolution of the ARJ21 wake vortices. The 3D vorticial structures were illustrated to analyse the near-ground evolution and far-field evolution of the wake vortices. The main findings are as follows.

Fig. 9.Iso-surface of λ2 = −0.5 at t* = 1.0: a case CL and b case HT_FLAP.

Fig. 10. Iso-surface of λ2 =−0.5 at t* = 5.0:a case CL and b case HT_FLAP.

Fig. 11. Iso-surface of λ2 =−0.5 at t* = 10.0:a case CL and b case HT_FLAP.

(1) In the near-ground phase, the main wing, flap and horizontal tail of an ARJ21 each produce a pair of wake vortices (i.e.wing tip vortices, flap vortices and horizontal tail vortices, respectively). The horizontal tail vortices are opposite to the other two vortex pairs due to the negative lift. The horizontal tail vortices are also the weakest and rapidly dissipate, whereas the flap vortices are the strongest and induce the tip vortices to merge with them. The flow structures and axial velocity distribution of the present ARJ21 model are similar to those obtained using only a one lift-drag model after the three pairs of vortices merge into a pair of main vortices.

(2) Due to the rapid dissipation of the horizontal tail vortices and merging of the flap vortices and wing tip vortices, the flap and horizontal tail of an ARJ21 have no major influence on the time history of circulation, attitude and trajectory of the wake vortices.

Fig.12. Comparison of a the temporal evolution of circulation(non-dimensionalised by Γ0), b the temporal evolution of wake vortex altitude(non-dimensionalised by b0) and c the trajectory of wake vortex cores.

(3) Specific configurations of an ARJ21 represented by the three lift-drag models have no significant effect on the far-field evolution of the wake vortices. A specific model represented by multiple lift-drag models can therefore be replaced by a single lift-drag model with the same weight and size. Analysis of the wake vortex evolution of ARJ21 airplanes can serve as a reference for aircraft with similar weight and size.

Acknowledgement

We would like to acknowledge financial support from the National Natural Science Foundation of China (Grant 91752205),Civil Aviation Joint Fund of NSFC (Grant U1733203) and Civil Aviation Safety Capacity Building Project (Grant TM 2019-16-1/3).