Influence of wing flexibility on the aerodynamic performance of a tethered flapping bumblebee

Hung Truong, Thoms Engels, Dmitry Kolomenskiy, Ki Shneider,*

a Aix-Marseille Université, CNRS, Centrale Marseille, I2M, Marseille, France

b University of Rostock, Institute of Biosciences, Animal Physiology, Rostock, Germany

c Global Scientific Information and Computing Center, Tokyo Institute of Technology, Meguroku, Tokyo, Japan

Keywords:Insect flight Wing elasticity Mass-spring model Fluid-structure interaction Spectral method Volume penalization method

ABSTRACT The sophisticated structures of flapping insect wings make it challenging to study the role of wing flexibility in insect flight. In this study, a mass-spring system is used to model wing structural dynamics as a thin, flexible membrane supported by a network of veins. The vein mechanical properties can be estimated based on their diameters and the Young's modulus of cuticle. In order to analyze the effect of wing flexibility, the Young's modulus is varied to make a comparison between two different wing models that we refer to as flexible and highly flexible. The wing models are coupled with a pseudo-spectral code solving the incompressible Navier–Stokes equations,allowing us to investigate the influence of wing deformation on the aerodynamic efficiency of a tethered flapping bumblebee. Compared to the bumblebee model with rigid wings, the one with flexible wings flies more efficiently, characterized by a larger lift-to-power ratio.©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

The spectacular flight capabilities of insects and the significant deformation of their flexible wings have triggered many studies and attracted numerous scientists of different fields. From an aerodynamic point of view, flapping wings are distinct from fixed wing airplanes. A prominent feature of flapping flight is the important role of the leading edge vortex (LEV) [1] which generates enhanced lift compared to steady aerodynamics, even at high angles of attack. The development of micro-air-vehicles (MAVs)with flapping wings is bio-inspired and has different technological applications, e.g. allowing the remote observation of hazardous environments inaccessible to ground vehicles. Most numerical investigations consider rigid wings to reduce the complexity of simulations. The nonlinear interaction of the composite wing structures, which are anisotropic, and the surrounding air requires detailed mathematical modeling and is challenging.Some experimental and few numerical studies have been carried out during the last decades and the conclusions were partly contradictory. It was shown that passive deformations enhance lift production in bumblebees by artificially stiffening their wings using a micro-splint by Mountcastle and Combes [2]. Experimental methods were used in Campos et al. [3] and Fu et al. [4]and they found that highly flexible wings exhibit significant tiproot lag which weakens vortices and thus reduces the force production. Numerical simulations by Du and Sun [5] solving the Navier–Stokes equations coupled with measured wing deformation data compared the results with the rigid counterparts. They concluded a 10% increase in lift caused by the camber deformation and a 5% reduction in required power.

The current work is motivated by and a follow up of the computations presented in Ref. [6]. There, we studied a flexible bumblebee wing rotating around a hinge point at the angle of attack equal to 45◦. We integrated a solid model based on massspring systems. The wing was modeled by a network of mass points which were connected by extension and bending springs.The method allowed us to take into account the wing flexibility when studying the aerodynamics of insect flight. Flexible and highly flexible wings corresponding to different stiffness values were considered. The results showed that the flexible wing produces less lift than the rigid wing. However, the latter has a better lift-to-drag ratio. On the contrary, the highly flexible wing experienced a strong tip-root lag caused by twisting. Consequently,it behaves poorly in terms of aerodynamic performance reflected in a much smaller lift and lift-to-drag ratio. Even though the study provided us some ideas about the impact of wing flexibility on the force generation, the revolving wing motion remains too simple to understand the complicated dynamics of a flapping wing. The revolving wing quickly attains a steady state and its dynamic deformation hardly plays a role in the force production. The wing kinematics of flapping insects is more complex,characterized by the flapping amplitude, wingbeat frequency,angle of attack, etc. These features strongly impact on the ability of generating lift and drag forces of the wings. Kang and Shyy [7]showed that the ratio between the flapping frequency and the first natural frequency of a flexible wing can yield advanced,symmetric or delayed rotation modes which in turn alter the resulting lift. Experiments were performed by Zhao et al. [8] using simple isotropic flapping wings with various stiffness values at different angles of attack. At low angles of attack (20◦to 6 0◦),they found that flexible wings have similar aerodynamic performance as rigid wings do. However flexible wings outperformed their rigid counterparts at high angles of attack (up to 90◦).

The aim of the present work is to investigate the aerodynamic efficiency of the flexible bumblebee wing model [6] within a tethered flight context. The wing motion is based on kinematic measurements by Dudley and Ellington [9]. First results presented in Ref. [10] used a simplified wing model, which lead to some artifacts in the membrane deformation and the wing seemed unrealistic. The current model is improved to remove those artifacts by using different mesh structure. The resulting force and power time series are compared with those obtained for a rigid flat wing by Engels et al. [11]. The effects of the wing deformation and flexibility on the aerodynamic forces and power requirement of a flapping bumblebee can thus be assessed.

The remainder of the article is organized as follows. We present the numerical methods used for solving the governing equations of the flexible wing, the fluid flow and its coupling.Then the numerical set-up and the bumblebee model is presents. The numerical results are discussed at last.

For studying the aerodynamic effects of flexibility in flapping wings, both the wing dynamics and the surrounding flow need to be modeled. This section will present the numerical methods for solving this fluid-structure interaction problem.

Solid solver using mass-spring system

The building blocks of insect wings are membranes and veins. The resulting sophisticated composite structures have nonlinear anisotropic properties coming from the truss framework composed of horizontal and vertical veins connected by membranes [12]. Modelling the mechanical behaviour of insect wings is difficult. To mimic the dynamic behaviour of the complex membrane-vein network, we use a mass-spring system taking into account the different mechanical properties of the components [6]. Veins can be considered as rods resisting mainly the torsion and bending deformation. On the contrary, the membrane behaves like a piece of fabric that resists stretch deformation.

Mass-spring models are an established approach for modeling of mechanical structures, distinguished by their computing efficiency and ability to handle large deformations. The discretization of the wing uses mass pointsmi(i=1,2,...,n) connected by springs. There are different types of springs and our model is based on bending and extension springs. At a given timet,the dynamic behaviour of the mass-spring system is defined by the position xiand velocity viof the mass pointi. It is governed by:

wherenis the number of mass points,is the internal force andis the external force acting on thei-th mass point,miand aiare mass and acceleration of thei-th mass point,respectively.

The system Eq. (1) is then advanced numerically in time by applying a second order backward differentiation scheme with variable time steps [13]:

Fluid solver and volume penalization method

The Reynolds number of insect flight typically lies in the rang e of O (101)and O(104).The bumblebee studied here has a Reynolds number of about 2000. Thus the fluid flow is accessible for direct numerical simulation, resolving all scales of motion. It is governed by the penalized incompressible Navier–Stokes equations [14],

which are solved on a Cartesian grid in a rectangular cuboid Ω.In the above Eqs. (3)-(5), u is the fluid velocity, ω =∇×u the vorticity,the total pressure andνthe kinematic viscosity.

The penalization and sponge terms in the momentum equation are added to impose the boundary conditions in the complex and time varying geometry. The latter is added to damp the wake flow and to remove the periodicity of the Fourier discretization, which affects the upstream inflow. The penalization term allows to impose the no-slip boundary conditions on the fluidsolid interface, as explained in Ref. [15]. The mask function χ contains all geometrical information of the solid and is given by:

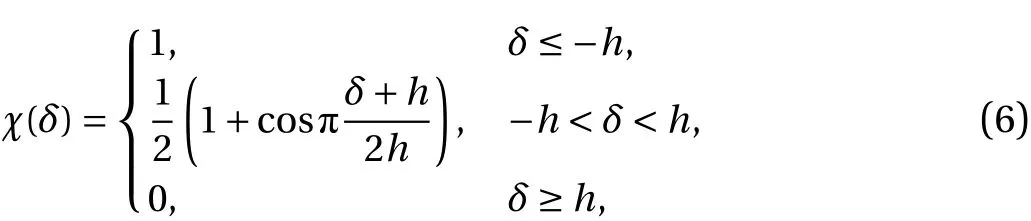
where δ is the signed distance to the fluid-solid interface.Oscillating forces in the case of moving solid bodies are avoided using a smoothing layer with thickness 2hwhich yields a smooth mask function [16].

The penalized Navier–Stokes Eqs. (3)-(5) are discretized with a Fourier pseudo-spectral method, expanding velocity, pressure and vorticity as truncated Fourier series, i.e.,and minimizing the weighted residual, yields a system of nonlinear ordinary differential equations (ODEs) for the unknown Fourier coefficients of the velocity. Hereis the wavevector andThe Fourier coefficientsof a quantityqcan be computed efficiently on massively parallel computers with the fast Fourier transform(FFT) using the P3DFFT library [17]. The Fourier spectral method is characterized by its high numerical precision and the absence of numerical dissipation and diffusion errors. Moreover,the solution of linear systems for imposing the incompressibility is avoided, as the Laplace operator can be inverted by a simple division. The quadratic nonlinear term is evaluated in physical space and the aliasing error are fully removed using the 2/3 rule.Details on the implementation in the FLUSI code1FLUSI: freely available for noncommercial use from GitHub(https://github.com/pseudospectators/FLUSI).can be found in Ref. [15].

Fluid-structure interaction

Time integration of the coupled fluid-solid system is using a semi-implicit staggered [18]. The fluid flow is advanced using an explicit second order Adams–Bashforth schemes (AB2) and integrating factors for the viscous term. The numerical stiffness of the solid model calls for a fully implicit time integration and a second order backwards differentiation formula (BDF2) is employed. The flowchart in Fig. 1 illustrates the coupling of solid and fluid solver. As shown in Refs. [19–21], the force for the solid deformation is dominated by the pressure contribution for the range of Reynolds numbers (75–4000). The viscous shear contribution can be considered negligible compared to the static pressure and is thus not taken into account. This semi-implicit staggered scheme, where the static pressure is computed from the previous time step of the solid model, is called weak coupling because it is conditionally stable. The solid has to be sufficiently heavy with respect to the fluid density, a condition which is fulfilled as we have the density ratio ρsolid/ρfluid=ρcuticle/ρair=1300/1.225=1061. The advantage of weak coupling is its efficiency, as the fluid and the solid need to be advanced only once at the current time level. Further details on the fluid-structure interaction (FSI) method including a detailed validation can be found in Ref. [6].

To study the influence of wing flexibility on the aerodynamic forces, we compare the flexible wings with rigid ones using the same numerical set up in previous work in Ref. [11].

Flow configuration

Figure 2 shows the computational domain of size 6R×4R×4RwhereRis the bumblebee wing length. The spacediscretization uses 1 152×768×768 grid points. Both, the translational and rotational motion of the insect body are disabled and the bumblebee is tethered at xcntr=(2R,2R,2R)T. The periodicity of the Fourier spectral method requires a thin vorticity sponge outlet, covering the last 4 grid points inx-direction. This damps out the wake and avoids the upstream influence of the computational domain. The value of the sponge penalization parameter is set toCsp=10−1, which is larger than the permeabilityCη=2.55×10−4. The sponge term is divergence-free and thus avoids the non local influence on the pressure field. Details on the influence of the vorticity sponge are given in Ref. [15]. A head wind with a mean flow accounting for the forward velocity of the insect, u∞=(1.246R f,0,0)T, wherefis the wingbeat frequency, is imposed in the entire computational domain by simply fixing the zeroth Fourier mode of the velocity u [18].

Bumblebee model

The bumblebee model here is the same as the one used in Ref. [22] and derived from case BB01 in Ref. [9], except for the wings which will be introduced later.

The bumblebee is composed of rigid components including the head, thorax, abdomen, all legs, proboscis and antennae.These parts are circular elliptical or cylindrical sections joined by spheres, and bilateral symmetry is assumed. The animals'body mass,M, is 175 mg, the gravitational accelerationg=9.81 m/s2. Based on the measured data from Ref. [23], the wing lengthR=15 mm which is slightly bigger than the rigid wing (withR=13.2 mm) used in Ref. [22]. The Reynolds number is defined byRe=Utipcm/νair=2685, whereUtip=2ΦR f=9.15 m/s is the mean wingtip velocity,cm=4.6 mm the mean chord length,νair=1.568×10−5m2/s is the kinematic viscosity of air,f=152 Hz (T=1/f=6.6 ms) is the wingbeat frequency (Tis duration)andϕ=115◦is the wingbeat amplitude. The wingbeat kinematics are prescribed based on the measured data of Dudley and Ellington [9].

Fig. 2. Computational domain of size 6 R×4R×4R used in all simulations.A bumblebeemodel withflexiblewingsistethered at xcntr=(2R,2R,2R)Tinaflow with themeanflowvelocity u∞=(1.246R f,0,0)T. A vorticity sponge region is placed at the outlet to damp out vortices. Periodic boundary conditions are set for the four other sides of the domain.

Flexible wing model

The two flexible wings of the insect are modeled using the mass-spring system as detailed in Ref. [6]. In the following we describe the venation pattern, the mass distribution and the flexural rigidity of the veins.

Venation pattern

The venation pattern plays a crucial role for the wing dynamics during flapping flight and is alleged to be responsible for the anisotropic properties of the wing. This motivates the use of a functional approach which reflects the vein network directly in the mass-spring model and is adapted from Ref. [23] including the wing contour. For discretization of the wing, a triangular mesh with 1 065 mass points is used, as shown in Fig. 6. The mesh is generated with the open-source integration platform SALOME2https://www.salome-platform.org/. In Ref. [6], we performed a mesh convergence study for the revolving motion, comparing between two wings, discretized by 4 65 and 1 065 mass points. We found that the coarsemesh wing showed no major difference with respect to the finemesh wing concerning the generated aerodynamic forces.However, in the present case, a fine-mesh wing is required for the pressure interpolation, as for the flapping motion the pressure field is expected to be more unstable.

Membrane

Fig. 3. Illustration of two adjacent triangles of the unstructured triangular mesh. The mass points are represented by the circles while the extension springs are represented by the continuous lines and the dashed line (crossover spring). The upper figures are the previous triangular mesh a without crossover spring and the currently used triangular mesh b with crossover spring in 2D. The lower figure illustrates the role of crossover spring for creating bending stiffness of the surface.

In our previous work [6], a mass-spring system composed of mass points and extension springs with an unstructured triangular mesh was used to model the membrane. By construction,every four neighboring pointsi,j,k,lform two adjacent triangles as shown in Fig. 3a. The limitation of this model is that the bending stiffness of the wing membrane is not taken into account. As a result, when the wing is under large forces, e.g. during wing rotation at the end of the downstroke, folds and wrinkles are observed at the trailing edge and the tip of the wing(Fig. 4a). These undesired deformations make the wing look unrealistic and affect the force production. To overcome this, the bending stiffness is added to the current model to prevent such folds and wrinkles.

Unlike the tensile stiffness, which involves computing inplane deformations and forces, the modeling of the bending stiffness of a sheet is rather more complicated because it requires computing out-of-plane forces normal to the deformed surface. There are two main methods have been proposed in the literature to deal with this problem. The first one is to model precisely the bending stiffness of the sheet by applying bending momentum which is inversely proportional to the angle between two adjacent mesh elements. Although this approach can result in a good accuracy, the evaluation of bending forces is costly and it can reduce the numerical performance of the mass-spring system [24]. On the other hand, the second approach is much simpler where a crossover spring is added between the two triangles from vertexito vertexjas shown by the dashed line in Fig. 3b.When a bending deformation occurs, the added spring will apply forces to these two vertices to resist the bending. This method is claimed to be inaccurate in some cases when the bending is too small or too large [24]. However for our problem, the method is confirmed to work effectively. The folds and the wrinkles are no longer observed during wing rotation while the numerical efficiency of the model remains almost as effective as the old model. These changes of wing shape in turn affect the force production of the wing, especially during stroke reversals as shown in Fig. 5.

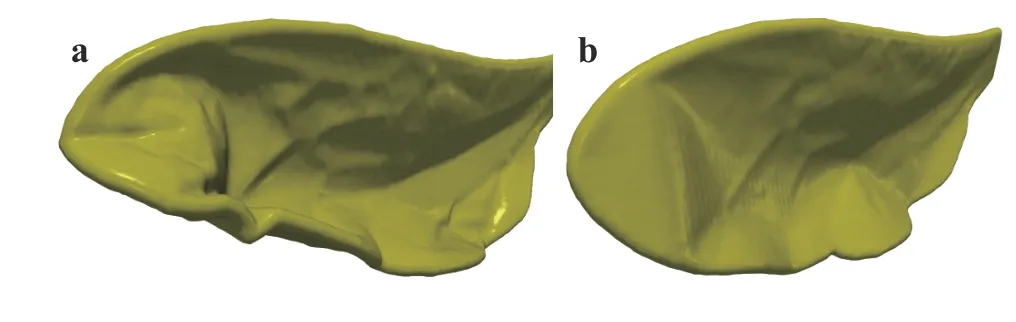
Fig. 4. Wing deformation during the stroke reversal at the end of the downstroke. a Old model without crossover springs. b New model with crossover springs.

Fig. 5. Vertical force and horizontal force, normalised by F=ρairR4 f 2, generated by the old wing model without crossover springs (continuous red line) and the new wing model with crossover springs (dash-dot blue line). The new wing generates more force than the old one during stroke reversal.

Mass distribution

The inertia of the wing is directly related to the mass distribution and the position of the mass center plays an important role for the wing dynamics. Based on measured wing mass data [23]and the venation pattern, the mass distribution can be determined. Similar to what has been done in Ref. [23], we choose the total mass of the wing to bemw=0.791 mg and according to the geometry it is distributed into the vein and membrane components. The veins are modeled as rods with circular cross sections with diameterdvand lengthlv, made out of cuticle,ρc=1300 kg/m3[23]. Accordingly their mass can be determined, the values are assembled in Tables 1 and 2. We use dimensionless quantities for both the diameter and the mass,normalized respectively with the wing lengthRand the air densityρairR3.

To obtain the mass distribution of the membrane as close as possible to the experimental data of bumblebee wings [23], we use an optimization method [6]. The objective function is the difference between the mass center of the wing measured in the experiment [23] and the one calculated from the mass-spring model.For the mass pointmiat position [xi,yi], which is in the membrane,we obtain:

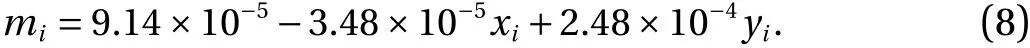
Differences between two centers of mass amount to 3 .85×10−3Rin thex-direction and 0 .93×10−3Rin they-direction. These are negligible compared to the reference wing lengthR.

Flexural rigidity of veins

Because the bending stiffness of the membrane is small, the flexural rigidity of the wing comes mainly from the flexural rigidityEIof veins which is calculated based on their material and geometry. While the estimation of their second moments of inertiaIis straight forward using the diameter data from Tables 1 and 2, determining the Young's modulus is not trivial. In our present work, the veins are considered to be made of cuticle which is reported to have a Young's modulus in the range of 1 kPa to 20 GPa [25]. The wing needs to be flexible enough to reveal the influence of wing flexibility to the aerodynamic performance of insects but it cannot be too flexible to show unrealistic mechanical behaviors. For these reasons, two values of the Young's modulusEare used: 7 GPa and 0.7 MPa, corresponding to flexible and highly flexible wing models, respectively.

The aerodynamic forces and the corresponding power consumption of the bumblebee model with flexible wings and highly flexible wings will be presented in this section. Moreover,with a view to the influence of wing flexibility on the insect aerodynamic performance, the results are compared with the ones obtained in Ref. [11] where the same bumblebee with rigid wings was studied. Figure 7(a-c) shows the vertical and horizontal forces as well as the aerodynamic power computed using rigid,flexible and highly flexible wings. For the purpose of comparison, the forces are normalised byF=ρairR4f2and the aerodynamic power byP=ρairR5f3. By the definition of the coordinate system, the positive of the vertical (horizontal) forces corres-pond to the lift (drag). The simulations are computed for 4 strokes with approximately 28800 time steps using 3 Intel Cascade Lake 6248 nodes (with 120 cores at 2.5 GHz) and consumed about 8200 CPU hours for each simulation. A visualization of the flow field and the deformation of the wing is shown in Fig. 8 for the case of high flexibility.

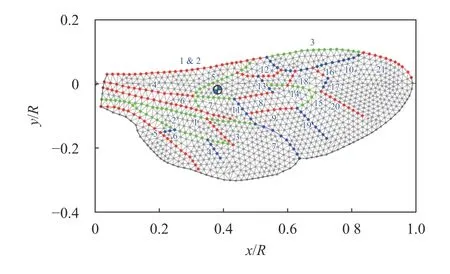
Fig. 6. Illustration of the mass-spring model which is meshed based on measured data of real bumblebee wings [23]. The blue and white marker represents the mass center. Color codes (red, green and blue) are used for identifying the veins and the membranes are represented by gray circles.

Table 1 Dimensionless vein diameter d v (adapted from Ref. [23])and their corresponding dimensionless mass m v for forewing.

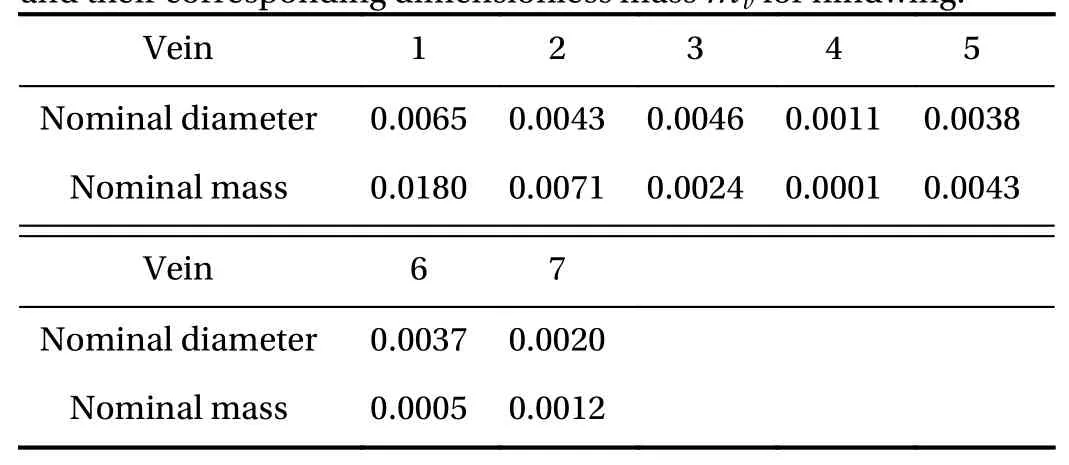
Table 2 Dimensionlessveindiameterdv(adaptedfrom Ref.[23])and t heir correspondingdimensionlessmassmvforhindwing.

Fig. 7. Vertical force, horizontal force (normalised by F =ρairR4 f 2)and aerodynamic power (normalised by P =ρairR5 f 3) generated by a bumblebee with rigid wings (continuous black) [22], flexible wing(dash-dot blue) and highly flexible (dash red). Circles represent the cycle-averaged value of forces and power.

Fig. 8. Visual ization of flow generated by a tethered flapping bumblebee with highly flexible wings in laminar flow at R e=2685 showing normalized absolute vorticity isosurfaces || ω||=100 (light blue). The flow field is plotted at time t =0.45/T. The vortices are only shown in the region 2 R≤y≤4R for the purpose of visualizing the deformation of the left wing.

Overall, the forces generated by the flexible wings tend to converge toward the forces generated by the rigid wings when the wing stiffness gets larger. Moreover, during one stroke, the more flexible the wing is, the weaker the peaks and the valleys of the forces at the ends of upstroke and downstroke get. These peaks and valleys can be explained by the sudden rotation of the wings during stroke reversals. Based on standard Kutta-Joukowski theory, Sane and Dickinson showed that the net forcegenerated by a rotating wing is proportional to the angular velocity of the wing [26, 27]. Since the motion of the rigid wing is imposed, every point on the wing rotates with the same angular velocity. This is no longer the case with the flexible wing. By taking the wing flexibility into account, the influence of the inertial and aerodynamic forces can now be observed. These forces resist against the movement of the wing, make the trailing edge bend in the opposite direction and create a negatively cambered wing compared to the flat rigid wing. This kind of deformation is predicted to weaken leading edge vorticity [8] and causes the wing to generate less force. Another way of looking at the problem is that the ability of adapting the wing shape helps to mitigate the large pressure jump between upper and lower surfaces, especially at the trailing edge [7] and provides a smoother flight [28, 29].

Table 3 Cycle-averaged forces and power calculated with three wing models: rigid [11], flexible and highly flexible.

For each stroke, the cycle-average values of the thrust, the lift and the required aerodynamic power are integrated and shown in Table 3. The effect on the average thrust of the wing flexibility can be considered negligible since these changes are quite small comparing to the fluctuations of the thrusts. On the other hand,the average lifts generated by the flexible and highly flexible wings are 12.44% and 25.68% smaller then the one of rigid wings,respectively. The decrease of the effective angle of attack caused by wing deformation can be understood as the reason for the declines of the average lift. The instantaneous angle of attack,which is claimed to play a significant role in the force generation[4], is altered by the shape adaptation of the wing during the flapping motion. However, it will be premature to conclude that that the rigid wings outperform aerodynamically their flexible counterparts based on these negative impacts on lift. Although the flexible wings generate smaller forces, they consume much less energy, with almost 18% and 29% required aerodynamic power are reduced for the flexible and highly flexible wings, respectively. Both flexible and highly flexible wings have better cycle-averaged lift-to-power ratios than the rigid wings (Table 3).Nevertheless, that does not necessarily mean that the more flexible the wing is, the higher lift-to-power ratio the wing attains since the flexible wings have a greater lift-to-power ratio than the highly flexible wings.

The impact of wing flexibility was studied by means of highresolution direct numerical simulation on massively parallel supercomputers. Tethered flight of bumblebees using flapping wing kinematics measured in experiments by Dudley and Ellington [9] was considered extending thus previous work on revolving flexible wings [6]. For this fluid-structure interaction problem, the fluid pseudo-spectral solver FLUSI with volume penalization was used and the flexible wing was modeled with an improved mass-spring approach.

A comparison of the aerodynamic forces and the power requirements between highly flexible, flexible and rigid wings showed that flexibility allows reducing the energetic cost of flapping flight characterized by the lift-to-power ratio. However, the highly flexible wing appears to be less efficient than the flexible wing. This can be interpreted that there is an optimized zone of wing flexibility, which is ideal for flying. Furthermore, the wing inertia contributes damping fluctuations in the aerodynamic forces and hence stabilizes the insect during flight.

The wing kinematics plays a crucial role for the aerodynamic performance. In our future studies, we are planning to investigate its influence in more detail. Other species, like Calliphora, for which in vivo measured wing kinematics and stiffness are available, will be likewise studied.

Acknowledgement

Financial support from the Agence Nationale de la Recherche (ANR) (Grant 15-CE40-0019) and Deutsche Forschungsgemeinschaft (DFG) (Grant SE 824/26-1), project AIFIT, is gratefully acknowledged. The authors were granted access to the HPC resources of IDRIS under the allocation No. 2018-91664 attributed by Grand Équipement National de Calcul Intensif (GENCI).For this work, Centre de Calcul Intensif d'Aix-Marseille is acknowledged for granting access to its high performance computing resources financed by the project Equip@Meso (No. ANR-10-EQPX-29-01). The authors thankfully acknowledge financial support granted by the ministères des Affaires étrangères et du développement international (MAEDI) et de l'Education nationale et l'enseignement supérieur, de la recherche et de l'innovation (MENESRI), and the Deutscher Akademischer Austauschdienst (DAAD) within the French-German Procope project FIFIT.

D.K. gratefully acknowledges financial support from the JSPS KAKENHI Grant No. JP18K13693.