A modified Lin equation for the energy balance in isotropic turbulence W.D. McComb*

Keywords:Turbulence Isotropic-turbulence Dissipation Inertial-transfer Scale-invariance

ABSTRACT At sufficiently large Reynolds numbers, turbulence is expected to exhibit scale-invariance in an intermediate ("inertial") range of wavenumbers, as shown by power law behavior of the energy spectrum and also by a constant rate of energy transfer through wavenumber. However, there is an apparent contradiction between the definition of the energy flux (i.e., the integral of the transfer spectrum) and the observed behavior of the transfer spectrum itself. This is because the transfer spectrum T(k) is invariably found to have a zero-crossing at a single point (at k = k*), implying that the corresponding energy flux cannot have an extended plateau but must instead have a maximum value at k = k*. This behavior was formulated as a paradox and resolved by the introduction of filtered/partitioned transfer spectra, which exploited the symmetries of the triadic interactions (J.Phys. A: Math. Theor., 2008). In this paper we consider the more general implications of that procedure for the spectral energy balance equation, also known as the Lin equation. It is argued that the resulting modified Lin equations (and their corresponding Navier–Stokes equations) offer a new starting point for both numerical and theoretical methods, which may lead to a better understanding of the underlying energy transfer processes in turbulence. In particular the filtered partitioned transfer spectra could provide a basis for a hybrid approach to the statistical closure problem, with the different spectra being tackled using different methods.©2020 The Authors. Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics. This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

We have previously written about the scale-invariance paradox and shown how it may be resolved by the introduction of filtered-partitioned forms of the transfer spectra [1, 2]. In the present paper we carry on this work to show how the underlying symmetries of the triadic interactions in wavenumber space also have implications for any more general study of the Lin equation. We have remarked elsewhere that to treat the Lin equation as purely a local energy balance equation is to be in danger of failing to realize that it is actually a highly non-local equation which couples all modes together. It is in fact the basis of the cascade picture of turbulent energy transfer, and it is important to always bear in mind that the transfer spectrum can be written as an integral over all wavenumbers of a term containing the triple-moment. In the present work we will argue that it is desirable to extend this scrutiny to the filtered-partitioned forms of the transfer spectrum in order to achieve a fuller understanding of the basic energy transfer processes.

This paper is organized as follows. We begin by stating the Lin equations and making some observations about the conventional interpretation of its role as an energy balance in wavenumber. Next we remind ourselves about the scale-invariance paradox and how it may be resolved. Then we move on to discussing the ways in which the Lin equation can be modified in order to clarify its role.

Lin equation

We begin with the (by now) well-known spectral energy balance equation in its most familiar form, thus:whereE(k,t) is the energy spectrum,T(k,t) is the energy transfer spectrum andνis the kinematic viscosity. A full derivation and discussion will be found in Ref. [2]. We will also follow the growing practice of referring to it as the Lin equation.

Now let us integrate each term of Eq. (1) with respect to wavenumber, from zero up to some arbitrarily chosen wavenumberκ:

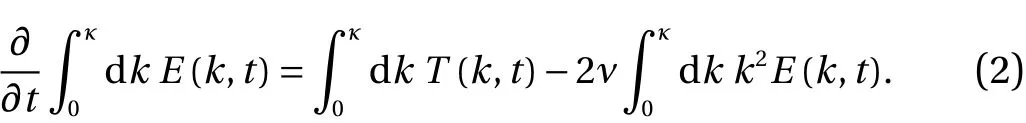
The energy transfer spectrum may be written as

where, as is well known,S(k,j;t) can be expressed in terms of the triple moment. Its antisymmetry under interchange ofkandjguarantees energy conservation in the form:

With some use of the antisymmetry ofS, along with Eq. (4),Eq. (2) may be written as

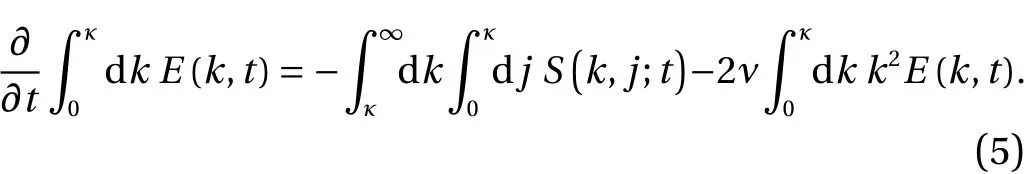
In this familiar form, the integral of the transfer term is readily interpreted as the net flux of energy from wavenumbers less thanκto those greater thanκ, at any timet. This the well known basis for the energy cascade.

It is usual to introduce a specific symbolΠfor this energy flux, thus:where the second equality follows from Eq. (4).

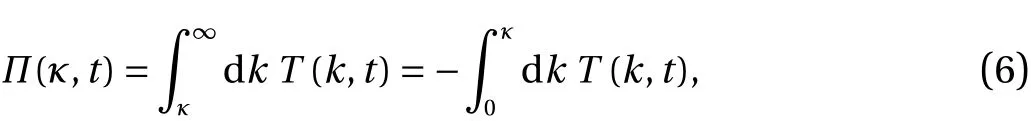
In order to consider the stationary case, we may introduce an input spectrumW(k). It is also convenient to introduce the dissipation spectrumD(k,t) such that:

With these introductions, and some rearrangement, we may write the energy balance equation as:

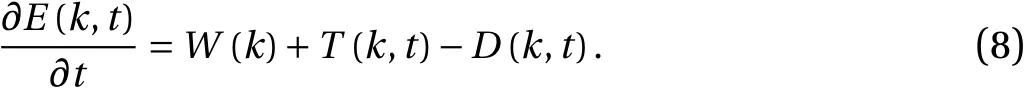
Figure 1 illustrates the general form of the energy transfers involved.

It should be noted that this general schematic form applies both to the stationary case and the case of free decay, with the input termI(k) being interpreted as appropriate to each case.

Paradox and its resolution

The inertial range of wavenumbers is defined as being where the time derivative (or input term) and the viscous term are negligible. Hence, from Eq. (1), it follows that the criterion for an inertial range of wavenumbers can be taken as the vanishing of the transfer spectrum; and, from Eq. (6), the constancy of the flux. In other words, for wavenumbersκin the inertial range we might expect to have have:

Scale invariance, can be summed up as the observation that the energy spectrum takes the form of a power law (which is in itself scale-free) and that there is a constant rate of energy transfer over a range of wavenumbers, which must necessarily be equal to the rate of energy dissipation. In practice, the second criterion of Eq. (9) is widely used to identify the inertial range.This criterion was first put forward in 1941 by Obukhov [3] and first used to derive the famous −5/3 spectrum using dimensional analysis by Onsager in 1945 [4]. More recently, the books by Leslie [5] and McComb [2, 6] all follow Kraichnan [7], and cite the criterion Π =ε; as does work by, for instance, Bowman [8],Thacker [9], and Falkovich [10]. However, the first criterion given in Eq. (9) only holds for a single wavenumber and this fact is the scale-invariance paradox.

There are two inertial-range criteria in Eq. (9); and, by elementary calculus, they seem to be equivalent. This point is illustrated in Fig. 2. It shows an extended region where the flux is constant and also the transfer spectrum is zero. This makes anappealingly simple picture of spectral energy transfers but unfortunately it is wrong. The transfer spectrum always passes through zero at a single point as illustrated in Fig. 1.

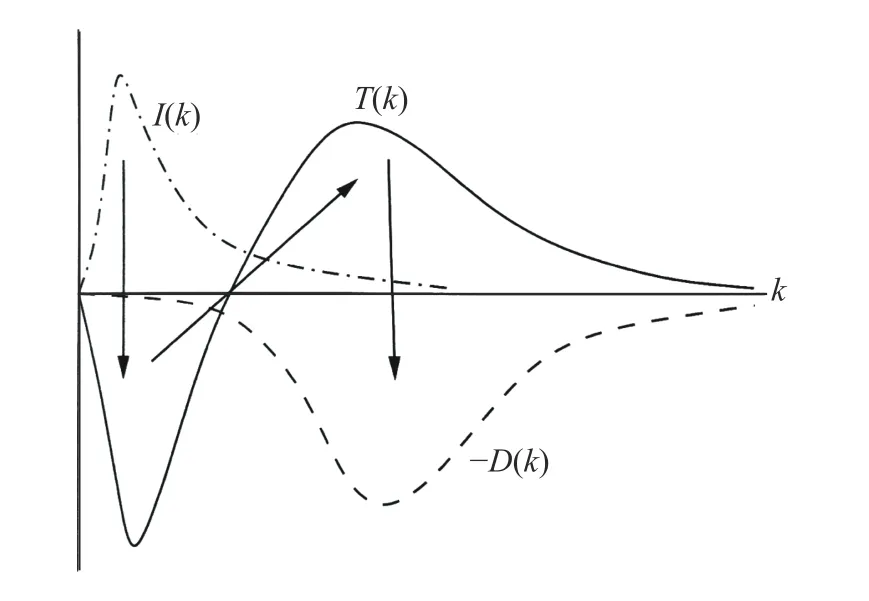
Fig. 1. Schematic view of the energy transfer in isotropic turbulence. The input spectrum I(k) can represent either the work spectrum W(k) or − ∂E(k,t)/∂t; or the combined effects of both terms.All the other symbols have their usual meaning as defined in the text.

This property ofT(k) was first discovered in 1963 by Uberoi[11] and later, extensive investigations confirmed that the transfer spectrum always has a single zero-crossing [12, 13] and pragmatic, approximate procedures were introduced to allow the inertial range to be identified from the behaviour of the transfer spectrum [14]. For a discussion of this topic, see Ref. [15].

So, let us consider again Eq. (5) for the transfer of energy from low wavenumbers to high. Now we wish to draw attention to the fact that, although the first term on the right hand side correctly represents the integral over wavenumberkof the transfer spectrum from zero up toκ, nevertheless the integrand is not actuallyT(k) (from now on, we shall suppress time arguments in the interests of conciseness). In fact the integrand represents some part ofT(k), because the internal integration with respect to the dummy variablejhas been truncated atj=κ.

In order to clarify this situation, it will be found helpful to introduce low- and high-pass filtering operations, based on a cutoff wavenumberk=κ, on the Fourier components of the velocity field. These operations are used for the study of spectral mode elimination in the context of large-eddy simulation and its associated subgrid modelling: see, for example, Ref. [16] and references therein. We are thus led to introduce transfer spectra which have been filtered with respect tokand which have had their integration overjpartitioned at the filter cut-off, i.e.j=κ:

We may define low-pass and high-pass filter functions, thus:

We may then decompose the transfer spectrum, as given by Eq.(3), into four constituent parts:

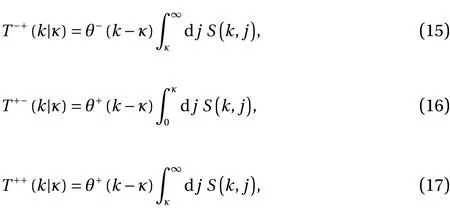
such that the overall requirement of energy conservation is satisfied:

It is readily verified that the individual filtered/partitioned transfer spectra have the following properties:

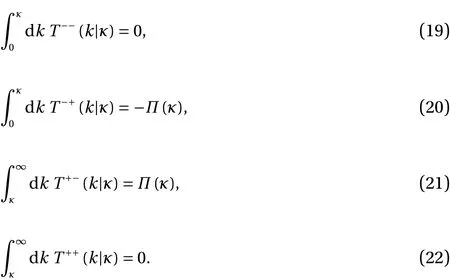
Equation (2) may be rewritten in terms of the filtered/partitioned transfer spectrum as:

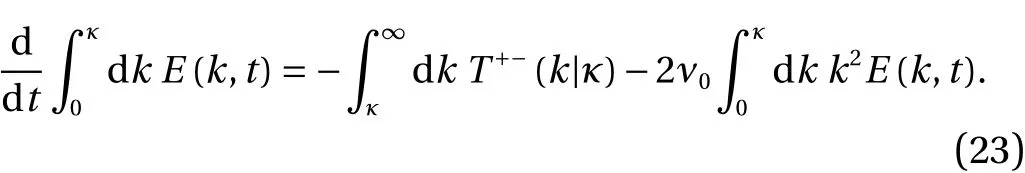
We note from Eq. (19) thatT−−(k|κ) is conservative on the interval[0,κ], and hence does not appear in Eq. (23), whileT−+(k|κ) has been replaced by −T+−(k|κ), using Eqs. (20) and (21).

Filtered and partitioned transfer spectra have been measured, using direct numerical simulation (DNS), in the context of spectral large-eddy simulation. In particular, Zhou and Vahala[17] found that the resolvable-scales energy transfer spectrumT<<(k) (i.e.T−−(k|κ) in our notation) is conservative on the interval 0 ≤k≤κ, in agreement with our Eq. (19); while the resolvable-subgrid transfer spectrum (i.e. ourT−+(k|κ)) is zero over a range of wavenumbers. Similar behaviour has also been found in the more detailed investigation by McComb and Young [18].

As we have previously pointed out in Ref. [1], experimentalists, who do not have access to partitioned versions of the transfer spectrum, will still find pragmatic procedures, such as the Lumley criterion for the inertial range [14], useful. However,those working with DNS or analytical theory, can avoid the paradox by changing their definition of energy fluxes, from those given by Eq. (6), to the forms1We should mention that these forms are exactly equivalent to Kraichan's original definition of what he called the transport power [7]. In later work [19],his definition of the transport power was equivalent to Eq. (6) in the present paper.:

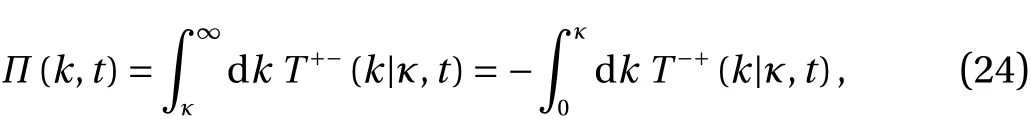
whereT+−(k|κ,t) is defined by Eq. (16) andT−+(k|κ,t) by Eq. (15).This is equivalent to Eq. (6); but, unlike it, avoids the paradox.This resolution of the paradox is shown schematically in Fig. 3.

Modifications to the Lin equation

In view of the above discussion, the obvious step now is to filter the energy spectrum in the same way as we have done for the transfer spectrum, and consider low-kand high-kforms of the Lin equation. In order to do this we make the decomposition:

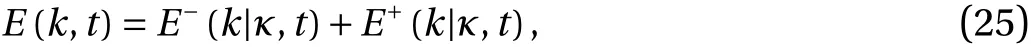
whereE−is defined fork≤κandE+is defined fork≥κ. Trivially,we can also do this for the input spectrumW(k) and dissipation spectrumD(k,t), and Eq. (8) can be written in low-kand high-kforms respectively, as:

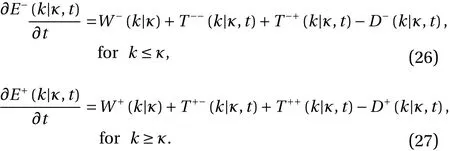
For this decomposition to be meaningful, the Reynolds number must be large enough for the inertial flux to be equal to the dissipation, in accordance with the second criterion of Eq. (9).As we increase the Reynolds number beyond this critical value,we have an increasing range of wavenumberskwhich satisfy that criterion, and this is the inertial range. We shall denote this range bykbot≤k≤ktop≡the inertial range of wavenumbers,where we now have to definekbotandktop. For sake of simplicity,we will consider stationary turbulence and omit the time variables.

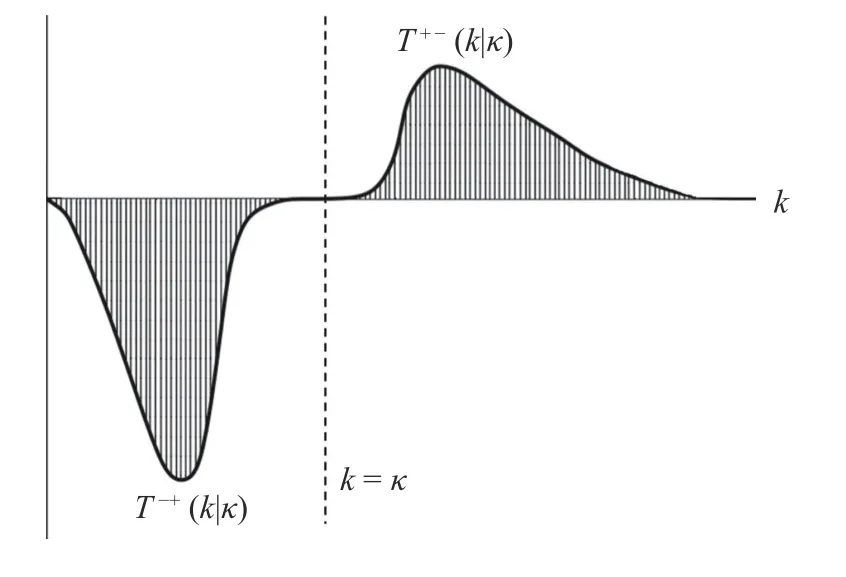
Fig. 3. Behaviour of the filtered-partitioned transfer spectra: the paradox resolved.

First, we need to consider the nature of the forcing spectrumW(k). In formulating the turbulence problem according to the tenets of statistical physics, this is normally taken to arise from the introduction of random stirring forces, which are assumed to be of white noise form. In particular, the forcing spectrum is taken to be peaked near the origin in wavenumber space, so that the turbulence that results from it is due to the Navier–Stokes equation, and not specifically related to the forcing. We should note that a different view was taken from the late 1970s onwards,in connection with the application of renormalization group methods to the Navier–Stokes equation. See either of the books[2, 6] for a general discussion of this point.

Accordingly, for theoretical approaches to the statistical closure problem, and also for direct numerical simulation, we should choose a form of forcing spectrumW(k) which satisfies the conditions:

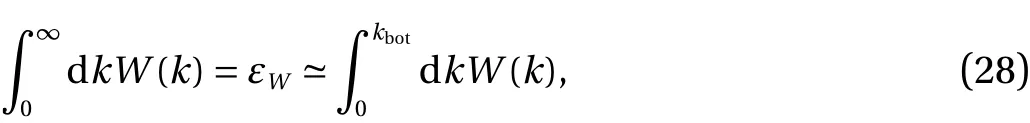
where the equality definesεW, while the approximate equality defineskbot, which we take to be the lower limit of the inertial range.

In general, we would requirekbotto be very much smaller than the Kolmogorov dissipation wavenumberkdwhich is generally taken as being an indicator of the dissipation range of wavenumbers. Experimenters have usually taken the the upper limit of the inertial range to be about 0.1kd−0.2kd. In fact we will definektopby another approximate equality, thus:

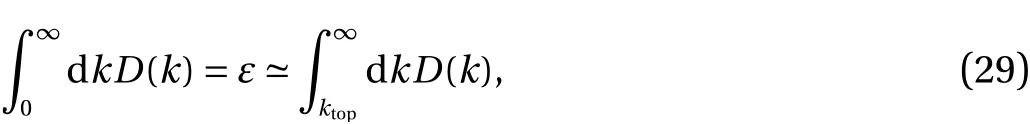
where the equality is the conventional definition of the dissipation rate, and the approximate equality defines the upper limit of the inertial rangektop.

With these points in mind, we may simplifly the lowwavenumber and high-wavenumber forms of the Lin equation to Eqs. (26) and (27), respectively:

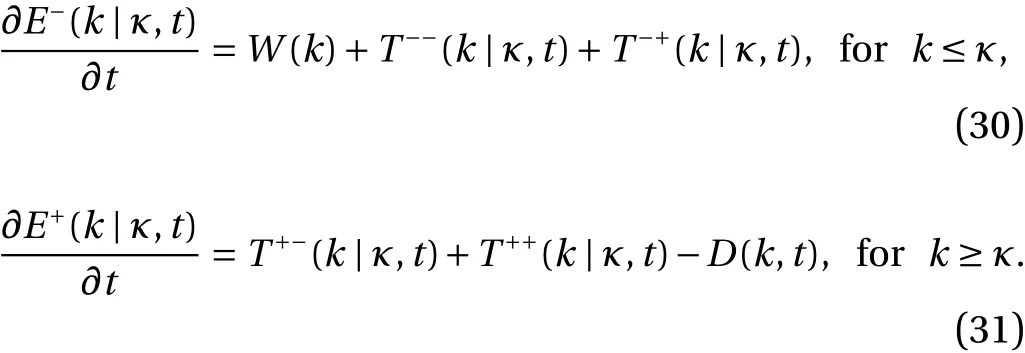
That is, for sufficiently high Reynolds numbers, and an appropriate choice of stirring forces, we may simplify matters by treating the input spectrum as being confined to the lowwavenumber region and the dissipation spectrum as being confined to the highwavenumber region. Deriving the flux balance equations from Eqs. (30) and (31), and invoking equations Eqs. (28) and (29), we obtain the final flux balances as:

Reminding ourselves that the transfer spectrum has its single zero crossing atk=k*, we may define the maximum value of the inertial flux as：

and at the same time introduce the useful symbolεTfor the maximum flux. Sincek*must lie within the inertial range, we can write the general criterion for the existence of the inertial range as:

For completeness it should be noted that this analysis is readily extended to the case of free decay, if we replaceεWby the energy decay rateεD. Further details may be found in Ref. [2].

Provided we are faced with the ideal situation, where the input and the output (i.e. dissipation) are well separated in wavenumber space, Eqs. (30) and (31) may provide a new, and one might hope, productive basis for the study of the energy transfers in isotropic turbulence. The corresponding partitioned-filtered Navier–Stokes equations are readily deduced and may be studied by direct numerical simulation as a four-component composite dynamical system, where the four components correspond to the four filtered partitioned transfer spectra.

Also, there is a growing use of hybrid approaches in fluid dynamics problems, and the closure problem could be approached in such a way by using different methods to tackle the different filtered-partitioned transfer spectra. For instance, in the low-ksystem, we might use the local energy transfer theory [20]forT−−(k), and renormalization group methods [21] forT−+(k); or,conceivably, the other way round! It would require investigation.

For the ideal situation just discussed, where we have the input and output (or, production and dissipation) ranges of wavenumber well separated, we need to choose the input spectrumW(k) to be peaked near the origin; and also we need the Reynolds number to be reasonably high. If for some reason, we cannot satisfy these conditions, then we must resort to Eqs. (26)and (27). However, even so, we must still have the Reynolds number large enough for the condition for the existence of an inertial range to be satisfied.

Lastly, I should emphasise that Fig. 3 is very much a schematic indication of how this graph should look, based on the small amount of information available to us. The behaviour of these filtered-partitioned transfer spectra was studied in the 1990s in the context of subgrid modelling and renormalization group methods: see Ref. [1] for references. Computers have advanced a lot since then, so we end with a plea to the effect that this field of study should be revived in the context of later work. An informal introduction to this topic may be found in the post of 23 July on the following weblog: blogs.ed.ac.uk/physicsof-turbulence/.

Acknowledgement

I wish to thank John Morgan who worked on this topic with me as part of his MPhys research project in the academic year 2018/19. It was John's idea to plot Fig. 3 in order to make the resolution of the scale-invariance paradox clearer and he also prepared the figures.