高中数学不等式易错题型解题技巧分析

祝永华

[摘要]高中数学不等式知识的应用较为广泛，不管是在选择题中，还是在填空题和计算题中都常出现不等式的题型.如果学生不能清楚地了解不等式的相关知识，不能完全掌握解题的技巧，就不可能更好地解题.文章针对不等式的几种易错题型进行探讨，并总结几点解题的技巧.

[关键词]高中数学;不等式;解题技巧

[中图分类号]G633.6

[文献标识码] A

[文章编号] 1674-6058（ 2020）35-0029-02

不等式是高中数学的主要内容，其题型极具多变性，很多学生都会出现误解的情况，无法解出正确的答案，这就需要教师引导学生掌握不等式易错题型的解题技巧，让学生的解题能力得到不断提高，

一、与线性规划相关的易错题型及解题技巧

不等式和线性规划相结合问题是不等式中比较常见的一种题型，其主要是对目标的最大值和最小值进行求解，在解答此种题型时，需要对面积进行求解以及定义域的相关知识进行掌握，需要了解不等式的性质和线性规划两者之间存在的联系.

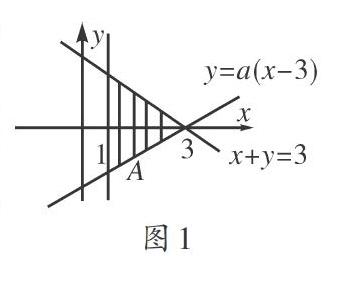
[例1]a>0，参数x，y，会满足下列三个条件，x+y≤3;x≥1;y≥a（x -3），如果z=2x+y的最小值是1，那么a的值是多少？

题目分析：这个题目是较为典型的一类不等式和线性规划相结合的题目，与普通的线性规划问题不同的是，此题优先给出了最值，然后根据最值来对某条直线的参数进行推理，这需要学生在实际解题的过程中，学会变换思维，进行逆向推理，在解题的过程中，可以绘制出如图1所示的坐标轴示意区，

解：当所求的目标函數经过A区域时，A点的坐标值为（1，-2a），那么将函数的目标值代入其中可知a=12.

总结：在解题时，要密切注意函数的最值问题，要明确其中所存在的不等式关系，并将相对应的可行范围画出来，上述题目中给出的参数a的取值范围是a>0，据此条件我们可以看出y=a（x -3）必然会经过第一象限和第三象限，这样我们就确定了三角形的可行域，再对可行域进行选择时也就不会出现方向错误的情况了，此种类型的题目中，一般会将目标参数设置成未知，以此促使题目的动态性和开放性得到增强，与一般的最值求解的区别在于，需要从结论人手对动态的图形进行分析，这也就要求解题者在解题的过程中找到关键点，再加上在目标函数的可行域中，我们已经知晓了求解的基本方向，进而达到了解题的目的，

二、与参数问题相关的易错题型及解题技巧

在所有的不等式类型题目中，与参数问题有关的不等式题目是难度较大的，在解题时要对题目中的未知参数进行考虑，在讲解这类题目时，教师可引导学生对未知的参数进行讨论，避免解题时出现疏漏.

[例2]求解不等式（x- 1）（x -a）<0.

题目分析：这是一个含有未知参数的不等式方程，解决这种题目重点是对未知参数进行讨论，也就是对a进行分类讨论，如果不能全面地进行分析，会使学生在解题中出现疏漏，导致解题的结果出现偏差，

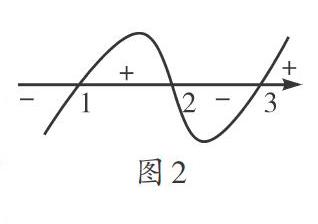
解：当a>1时，x的范围是1

[例3]求解不等式ax2-2x+1<0，已知a是参数，a∈R.

题目分析：此题与例2是相同的，也需要对未知参数a进行求解，首先需要做的就是要对a进行分类讨论，以确保解题的准确性和全面性，分析的过程与上题相同，也需要从a=0、a<0，a>0三个层面来进行分析，同时，当a>0时，需要对△的值进行区分，然后分别进行求解，

总结：当不等式中含有未知的参数时，最关键的步骤就是对未知参数进行分类讨论，这样才能使解题更加准确和全面，

三、与高次问题相关的易错题型及解题技巧

与高次问题相关的不等式问题是高中数学需要重点学习的内容，在解题的过程中最容易出错的地方就是区域划分容易混乱，不能准确地对特殊的区域或者是特殊的点进行判断，在遇到与高次问题相关的不等式题型时，可通过因式分解的方式解决，这样不仅可将复杂的问题进行简化，还可促使问题更加清晰明了，容易找到解题突破口，进而掌握解题的技巧，快速解决问题，

[例4]求解不等式（x- 1）（x - 2）（x -3）>0.

题目分析：这个不等式的结构是三次的，要比常见的二次结构要高，所以很多学生在解题时还是会利用公式进行求解，这样显然是难以达到解题目的的，必须要找到一种方便、简洁、高效的解决方式，

解：根据上述三次不等式方程，可画出图像（如图2），具体步骤：首先画出一个坐标轴，在坐标轴上标记出三个零点，即1、2、3，然后将坐标轴划分成4个区间;其次将靠近右边的区间看作是正，其他的看作是正负相间，在区间标明正负号;最后不等式大于0用“+”来表示，不等式小于0用“一”来表示，这样就可以更加形象地对不等式的区域进行观察，学生可明显地看到13，这就是题目最终的结果，

总结：这种解题方法我们称之为“穿根法”，采用此法需要在解题时画出坐标轴，然后在坐标轴上进行不等式情况的绘制，根据所画数轴的情况和穿线的顺序来对不等式的大小情况进行判断，此种解题方法更加直观和简单，降低了知识的难度，

四、与恒成立问题相关的易错题型及解题技巧

恒成立问题是数学常出现的一类题型，不仅与不等式有关系，还与其他的数据知识有着密切的联系，实际上，在对历届高考题目分析的过程中，我们通过总结恒成立的相关知识可知，不等式中的恒成立问题，是将抽象的函数知识以及数列知识进行结合所命制的题目，这种类型的题目有较强的逻辑性，解答这种类型的题目也较难，由于这种题型具有抽象性，如果学生的逻辑思维较差，就容易在求解的过程中出错，为了更准确、更快速地解答出与恒成立问题相关的不等式题目，需要对函数、导数、不等式、单调性等多种类型的知识点进行考虑，这样才能更好地解题.

[例5]假设函数f（x）= In（1+x），g（x）=xf'（x），x≥0，其中f'（x）是厂（x）的导函数.

1.当g1（x）=g（x），gn+1（x）=g（gn（x）），n是正数时，求出g（nx）的表达式.

2.当f（x）≥ag（x）是恒成立的，那么a的取值范围是多少？

3.假设n是正数时，试着比较g（1）+g（2）+…+g（n）与n-f（n）的大小，并进行证明，

题目分析：该题是一道典型的复合型数学题，主要结合函数、导数和不等式来求解闭区间上函数的最值，求解函数的单调性情况，具有很强的综合性，解题的关键在于进行适当变形或者采用分离变量、构造函数、变换主元等方式，借助基本不等式或者函数单调性等性质来达到求解的目的，而其中的最值问题主要是将其转化成基本不等式后进行求解;在转化不等式的过程中，要注意合理确定不等号的方向，避免因不等号方向不正确而导致解题错误，具体可记忆为“一正，二定，三相等”，

本文简单分析了四种不等式易错题型的解题方法技巧，总体来说在解答不等式题型的过程中，主要的方法技巧有以下几种：换元法、反证法、性质法和数形结合法，换元法是指利用某一个变量，将数学问题中的某个式子进行整体的替换，这样可有效地对题目进行简化，让学生更顺利地进行解答，反证法是在不等式不能正常推理的情况下常使用的一种方法，是通过反向推理的方式来对问题进行分析，以达到解题的目的，这种方法不仅可以解决不等式问题，还可以解决很多几何问题，性质法是指从不等式的基本性质出发，对题目进行分析，求出不等式的解，数形结合法是指利用坐标轴等图形将不等式题目中的信息表示出来，这样可使题目更加直观，学生也可以更直接地了解到题目信息，然后快速解题，在选用具体的不等式解题方法时，必须要结合题于信息和具体情况来合理选择，确保所选解题方法可以满足实际的解题需求，从而帮助我们更好地解决问题，避免在求解过程中出错，

总而言之，不等式题型具有一定的复杂性，出错率较高，因此，解题时学生必须要掌握各种类型不等式问题的解题技巧，找到题目中易错的点，然后应用合适的方法来解决问题，学生还需具有举一反三的思维，不断提高自身的解题经验，让自身的解题能力得到提高.

[参考文献]

[1]李严.高中数学不等式易错题型及解题技巧[J].亚太教育，2015（22）：50.

[2]高健成.简析高中数学不等式易错题型及解题技巧[J].亚太教育，2016（ 31）：54-55.

[3]王睿建.高中数学不等式易错题型及解题技巧[J].新一代.2017（7）：106.

[4]王家恒.高中数学不等式解题技巧教学[J].数学大世界（下旬），2018（4）：77.

[5]龔小霞.关于高中数学不等式恒成立问题的解题方法分 析[J].数理化解题研究，2015（19）：9.

（责任编辑陈 昕）