高中数学建模教学实践探究

高玉珊 凌中华

[摘要]数学建模是高中数学学科核心素养之一.研究数学建模对培养学生的数学应用能力具有重要意义.文章结合高中数学建模案例，对高中数学建模教学设计进行探究，对如何设计高中数学建模教学活动提出一些建议.

[关键词]高中数学;数学建模;线性回归

[中图分类号]G633.6

[文献标识码] A

[文章编号] 1674-6058（ 2020） 35-0004-02

数学建模是指对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程，《普通高中数学课程标准（2017年版）》把数学建模作为六个数学学科核心素养之一，指明数学建模主要表现为：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题，然而目前高中生的数学建模能力普遍较低.因此，高中数学建模课程的探究是高中数学教学的重要课题，

一、数学建模教学实践

1.建模问题

教师首先介绍数学建模的基础知识，结合一些贴近实际生活的简单数学问题，向学生讲解什么是数学模型，及建模的步骤.

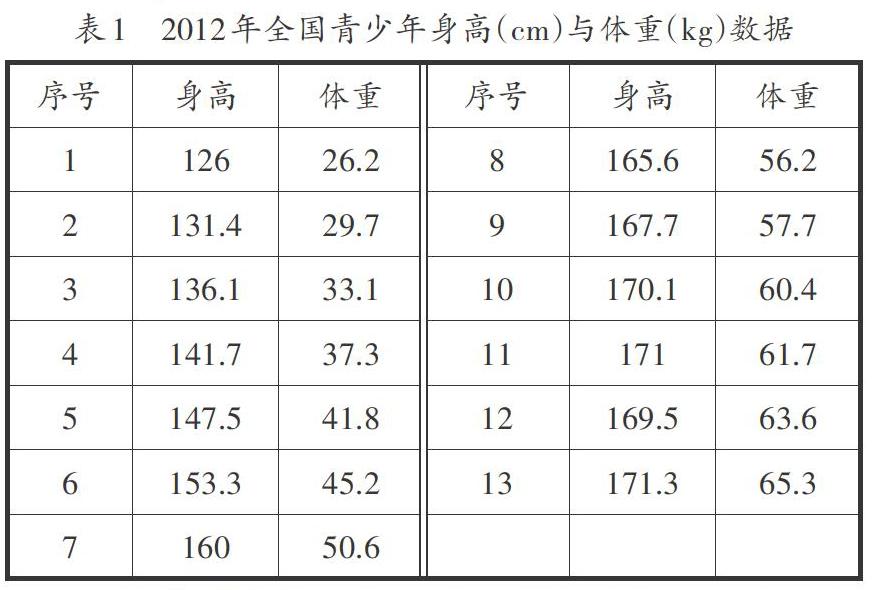
问题：常识告诉我们，人的身高越高，体重越重，那么平均来说，身高170 cm的人比身高160 cm的人体重大多少呢？表1是2012年全国青少年身高（cm）与体重（kg）的数据.

（1）根據数据作出散点图，讨论散点图呈现的趋势;

（2）选用一个函数来近似描述身高与体重的关系;

（3）预测身高170 cm的人比身高160 cm的人体重大多少呢？

面对这样一个现实问题，学生可能感到无从下手.教师可以根据解题思路，将问题分解为三个小问题，难度循序渐进，便于学生思考解答，从而激发学生的学习兴趣，树立学生的学习信心.

2.模型的建立

问题（1）和问题（2）已经给出了相对明确的解题方向，教师只要给予适当的引导，学生就容易找到问题的突破口，这两个问题的解答就是模型的建立过程.

问题（1）中给出了13组身高与体重的对应数据，要研究的是身高和体重之间存在的关系.因此，解决问题应紧紧围绕这两组数据展开.对数据进行处理，设身高为x厘米，体重为y千克，将数据转化为二元数组（xi，yi），i=1，2，…，13，于是可以用描点法在直角坐标系中作出散点图（如图1）.

观察图1可以发现，身高与体重的散点基本落在一条直线附近，我们可以推测身高和体重的数据具有正比例关系，可以用一次函数来描述，因此，设y=ax+b+ε①，其中a，b为未知的常数，ε=y- ax -b称为残差，表示在纵轴方向上的误差，这就是描述身高和体重的数学模型.

3.模型的求解

线性回归模型的求解过程是本节课的难点，需要教师引导学生分析清楚问题的本质，将实际问题转化成学生熟知的数学问题，

设问1：要预测身高170 cm的人比身高160 cm的人体重大多少，需要求解什么呢？

设计该问题的目的是让学生明确问题（3）实际是要将描述身高（x）和体重（y）关系的一次函数y=ax+b+ε的系数a，b确定下来.为此，需要利用二元数组（xi，yi），i=1，2，…，13来确定a，b的估计值a，b，进而给出回归方程y=ax+b和回归直线的概念，

设问2：过散点附近的直线有无数条直线，如何选取最佳的回归直线呢？即如何求出a，b的估计值a，b？

此问题的设计是为了突破本节课的难点，教师可以列出解决问题的几个不同方案，让学生比较、讨论各个方案的优劣，从而选出可行的方案，逐步引导学生探索出最小二乘法的思想.

5.模型的应用

在这个环节，可以让学生根据模型和自己的身高，比较模型的预测体重和真实体重的误差，并讨论产生误差的原因，

二、数学建模教学的反思

1.数学建模教学内容和过程的合理安排

《普通高中数学课程标准（2017年版）》提出数学课程的目标：学生能有意识地用数学语言表达现实世界，发现和提出问题，感悟数学与现实之间的关联，学会用数学模型解决实际问题，积累数学实践的经验，从中可以看出，高中数学建模目的不在于追求精确的结果，而在于培养学生的数学思维能力和数学应用意识.因此，数学建模课程内容的选取应该贴近学生的学习和生活，教学过程应专注于创设情境，合理设问，引导学生将实际问题转化为数学问题，并将求解结果应用于实际，培养学生的应用意识，而对于模型的求解，教师可以利用计算机辅助进行合理的模拟、计算等，避免课堂上进行复杂的推演、计算.

2.渗透数学史，增强课堂趣味性

高中生的数学建模能力普遍较低，数学建模过程要求学生具备模型假设能力、模型构成能力、模型求解能力、模型分析能力、模型检验能力等，这对高中生是一项极具挑战的活动，因此，会有学生因畏惧困难而学习动力不足，不专心听课，著名数学教育家弗赖登塔尔曾经这样描述数学的表达形式：没有一种数学的思想，以它被发现时的那个样子公开发表出来，一个问题被解决后，相应地发展为一种形式化技巧，结果把求解过程丢在一边，使得火热的发明变成冰冷的美丽，在教学过程中，教师结合所授内容，适当地引入相关的数学史，把冰冷的美丽变成火热的发明，可以加强学生理解和掌握数学的概念、定理的本质，同时可以激发学生的好奇心和求知欲，例如，在线性回归的教学中，可以介绍最小二乘法产生的历史过程，及英国统计学家高尔顿（F.Galton）和他的学生皮尔逊（ K.Pearson）研究父母身高与其子女身高的遗传问题的历史，进而介绍“回归”一词的由来.

[参考文献]

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.

[2]徐斌艳，Matthias Ludwig。中德学生数学建模能力水平的比较分析：以中国上海和德国巴登符腾堡州学生为例[J].上海教育科研，2008（8）：66-69.

[3]孙翔宇.上海市高中生数学建模能力的调查与分析[Jl.教育测量与评价，2016（6）：44-49.

（责任编辑黄桂坚）