基于高分辨率CT 征象预测230 例磨玻璃结节样肺腺癌浸润性的临床研究
2020-12-11黄洪磊薛昌辉
李 凤,黄洪磊,薛昌辉,王 英
(福建省南平市第一医院影像中心 福建 南平 353000)
随着现代CT 成像技术的发展,GGN 在胸部CT 检查中的检出率明显增加。有研究表明,肺腺癌是GGN 样表现的肺癌中最常见的组织病理学类型,其早期诊断及手术治疗可明显改善患者的预后[1]。因此,术前基于MSCT 征象评估及预测肺腺癌的浸润程度,对于指导临床和预测患者预后极为重要。
1 材料与方法
1.1 研究对象
回顾分析我院2015 年至2019 年病理证实的230 例GGN(共242 个GGN 病灶)的CT 资料。按照肺腺癌新分类标准[2]分为浸润前病变组包括不典型腺瘤样增生42 个、原位腺癌68 个;浸润性病变组包括微浸润腺癌32 个和浸润性腺癌100 个。101 例浸润前病变:男36 例,女65 例,年龄28 ~74 岁,平均(57.27±13.94)岁;129 例浸润性病变:男53例,女76例,年龄33~79岁,平均(59.00±11.62)岁。
1.2 CT 检查方法
使用西门子第二代炫速双源CT 进行扫描。参数:管电压120kV,管电流250mA,原始采集层厚0.6mm,层间隔4 ~6mm,矩阵512×512;窗宽1450 ~1500HU,窗位-450 ~-500HU。根据实际病灶密度适当调整窗位和窗宽。

表1 两组GGN 的主要CT 特征比较
1.3 图像分析及统计学方法
由2 名具有10 年以上影像诊断医师在双盲的情况下对病灶进行诊断,结果不一致时,双方协商作出决定。使用SPSS22.0 软件进行分析。计数资料采用χ2或Fisher检验,计量资料采用t检验。具有统计学差异的变量(P<0.05),进行二元Logistic 回归分析,并绘制ROC 曲线,计算出AUC,选出最佳诊断变量。
2 结果
2.1 两组GGN 的主要CT 征象比较
两组病灶分叶征、毛刺征、空泡征、血管集束征、瘤肺界面、病灶大小等存在统计学差异(P<0.05);两组的病灶形态、空气支气管征无统计学差异(P>0.05)(表1)。
2.2 二元logistic 回归分析
在本组二元Logistic 回归分析中,将浸润性腺癌作为因变量,病灶大小、形状、分叶征、毛刺征、空泡征、血管集束征及瘤肺界面作为协变量,分析结果显示大小、分叶征、空泡征、瘤肺界面为鉴别两者的重要因素(表2)。将上述影响因素应用二元Logistic 回归分析作出ROC 曲线,发现病灶大小及肺瘤界面具有最佳诊断性能图1。
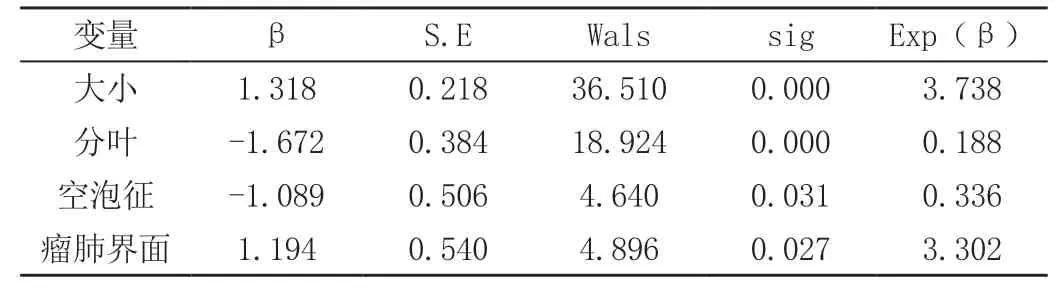
表2 二元logistic 回归分析
3 讨论
不同类型的肺腺癌在治疗方法、预后及总生存率上均有不同。因此,本研究通过分析GGN 的影像特征,探究不同征象的鉴别诊断价值。
本研究结果示GGN 形状及空气支气管征在两组间无统计学差异(P>0.05),这与之前的文献报道一致[3-4]。而病灶的大小、分叶征、毛刺征、空泡征、血管集束征在两组间均表现出显著统计学差异。相关研究发现[5-6]病灶分叶征、毛刺征提示其恶性程度较高[7-8]。空泡征是由于肿瘤细胞未完全破坏侵蚀小气道形成,其发生率与病变恶性程度正相关。血管集束征指其病理学基础肿瘤细胞向周围血管直接侵犯。本研究发现随着恶性程度进展,纤维成分增加从而导致血管受牵拉。但是在本研究结果中,空气支气管征在两组间无统计学差异(P>0.05),可能是由于本研究纳入的病例中mGGN 病例较少有关。
为进一步探究与GGN 样浸润性腺癌相关的危险因素,本研究进一步进行二元Logistic 回归分析,结果显示病灶大小、分叶征、空泡征、瘤肺界面为鉴别两者重要的因素。进一步研究显示病灶大小及肺瘤界面具有最佳诊断性能。病灶大小是评估肿瘤T 分期的关键指标,研究发现病灶越大其恶性程度越高。本研究显示,浸润性腺癌组的直径明显大于非浸润腺癌组。肺瘤界面其病理基础为随着病变进一步发展,肿瘤细胞和纤维基质变得越来越厚[9-10],肿瘤边缘越清晰。
综上所述,GGN 的大小、边界、分叶征、毛刺征、空泡征、血管集束征等MSCT 征象有助于诊断浸润性肺腺癌,其中病灶大小及瘤肺界面具有最佳诊断性能,能够为临床的精准诊断和治疗提供客观依据。
