基于组合聚类的智能汽车横向稳定性判别方法*
2020-12-08谷先广孟科委姚鑫鑫汪洪波
谷先广,孟科委,姚鑫鑫,汪洪波
(1.合肥工业大学汽车与交通工程学院,合肥 230009;2.合肥工业大学智能制造技术研究院,合肥 230009;3.太航常青汽车安全系统(苏州)股份有限公司,苏州 215100)
前言
近年来,无人驾驶车辆技术迅猛发展,智能汽车在军事及商业应用中取得了长足的进步,成为未来汽车研究热点[1]。 由于无人车行驶环境复杂多变,如弯道曲率过大、路面附着系数较低、横向风影响等诸多因素均对无人驾驶车辆行驶稳定性造成巨大挑战。 因此,在行驶过程中对车辆稳定性进行准确判断并加以控制是十分必要的。 车辆稳定性判据决定了车辆稳定控制系统的介入与退出时机,是车辆稳定性控制的基础[2-3]。 文献[4]中将车辆横摆动能和侧向运动动能之和定义为失稳动能,利用能量法推导出车辆失稳动能与纵向运动动能方程,基于相平面法提出车辆稳定性判据,进行车辆稳定性判定。文献[5]中提出了将Lyapunov 直接法应用于车辆横向稳定性分析,并提出两个新的Lyapunov 函数,用于车辆稳定性判断,且估算的稳定区域增大。 文献[6]中在基于传统双线法确定的稳定域中引入横摆角速度法确定的稳定域,设计了一种基于相平面法的联合车辆稳定性判据。 文献[7]中提出一种利用间隔分析法确定车辆行驶稳定域,综合轮胎载荷转移率LTR、纵向滑移率、轮胎侧偏角确定稳定域的边界阈值,通过分析模拟数据验证了该方法的有效性。
目前常用的车辆稳定性判据大多依靠部分车辆状态参数建立,本文中在充分考虑车辆行驶状态参数基础上,通过仿真提取了表征车辆横向稳定性的相关行驶状态参数数据。 应用自组织特征映射(self-origanizing feature mapping, SOFM)神经网络和K 均值聚类法相结合的聚类分析技术[8-9]对数据进行分类,确定各离线聚类中心表征的稳定性等级,采用均值法更新聚类中心进行在线横向稳定性判别。最后以判别结果为依据指导稳定性控制策略介入控制,通过仿真和试验验证了所提出的基于组合聚类的车辆横向稳定性判别方法的有效性。
1 理论基础
1.1 SOFM 算法
SOFM 神经网络是一种竞争式学习网络,其基本思想是使输入样本通过竞争学习训练后,功能相同的输入靠近,而不同的分开,以此将无规则的输入自动排开[10]。 SOFM 神经网络结构如图1 所示。SOFM 算法原理如下。
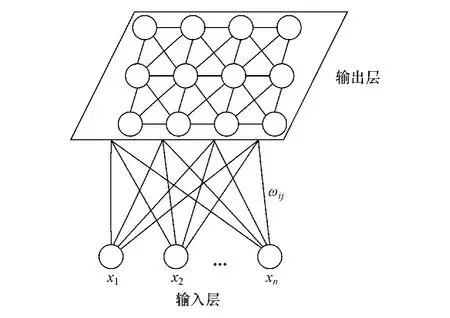
图1 SOFM 网络结构图
(1)初始化 对神经元间连接权值ωij赋予(0,1)随机数,确定初始优胜邻域sj(t) ,确定总训练次数T和学习率η(t) 初值。
(2)输入样本 确定神经网络输入样本:
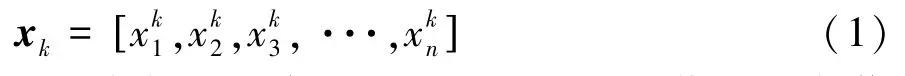
(3)确定获胜神经元 以欧式距离作为判断依据,计算输入样本与输出神经元之间的欧式距离Dj:
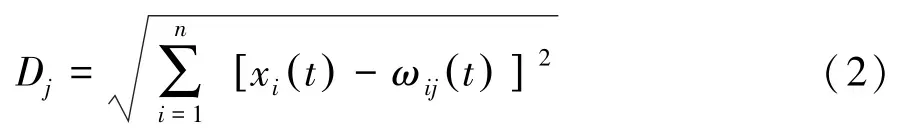
获胜神经元k需满足欧氏距离Dj最小,即满足Dk =min(Dj) 。
(4)调整权值 在优胜邻域内根据距离获胜神经元k的距离远近调整神经元连接权值:
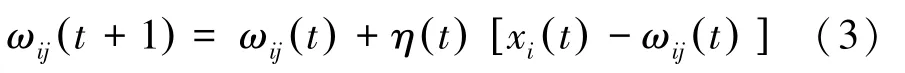
调整学习率η(t +1) 和邻域函数sk(t +1) 。
(5)若满足精度要求或达到最大训练次数,则输出聚类结果;否则,重复步骤(2)~步骤(4)。
1.2 K-means 聚类算法
K 均值聚类算法是一种迭代求解的聚类方法,迭代过程中不断移动簇内样本,使簇内样本相似度较高,而簇间样本相似度较低,最终实现样本分类[11-12]。 算法实现过程如下:
(1)确定聚类数目K,从待聚类样本集中选取k个样本作为初始的聚类中心(y1,y2,…,yk) 。
(2)以最小欧氏距离为划分准则,计算样本点与聚类中心间的距离,划分样本。 欧式距离计算如下:
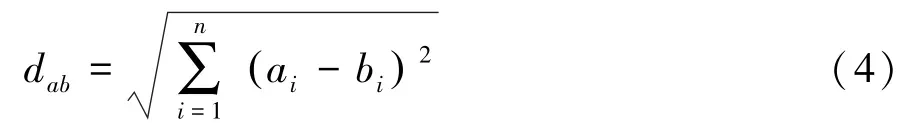
式中ai和bi分别为样本a、b的变量值。
(3)计算每个簇中对象平均值,更新聚类中心。
(4)重复步骤(1)~步骤(3),直到满足聚类结果精度要求或达到最大迭代步数时停止迭代,输出聚类结果。
分析发现,SOFM 神经网络算法虽然计算简洁却难以得到精确的聚类信息,但可以通过训练提高样本的可聚类性。 而K 均值聚类算法简单高效,在已知初始聚类中心情况下具有较高的精确度,但聚类结果受初始中心的选取影响较大,易陷入局部最优解。
基于两种算法的优缺点将二者进行有机组合用于车辆横向稳定性判别方法的构建上。 利用SOFM神经网络对待聚类样本集进行训练,实现数据样本的初聚类。 当网络收敛时,竞争层神经元对应的连接权值成为不同类别输入的中心,将之作为K 均值聚类算法的初始聚类中心,利用K 均值聚类算法完成样本数据最终分类。
2 稳定性判别方法建立
2.1 聚类分析数据库建立
2.1.1 车辆动力学模型建立
在 CarSim 软件中选择 E-Class,Sedan 车型,根据需要对车辆参数进行修改。 整车动力学模型基本参数如表1 所示。

表1 整车动力学模型参数
为便于后续对提出的稳定性判别方法的评价分析,轮胎模型采用CarSim 内置的MF-Tyre 模型,该模型采用魔术公式[13]对轮胎进行建模,拟合公式为

式中:F可以表示纵向力、侧向力和回正力矩;x为纵向滑移率或轮胎侧偏角;B、C、D、E分别为刚度因子、曲线形状因子、峰值因子和曲线曲率因子。
2.1.2 驾驶员模型建立
轨迹跟踪是智能汽车道路行驶的核心技术之一,在车辆匀速行驶基础上,建立基于轨迹预测的驾驶员方向控制模型[14]实现智能汽车的轨迹跟踪控制,如图2 所示。
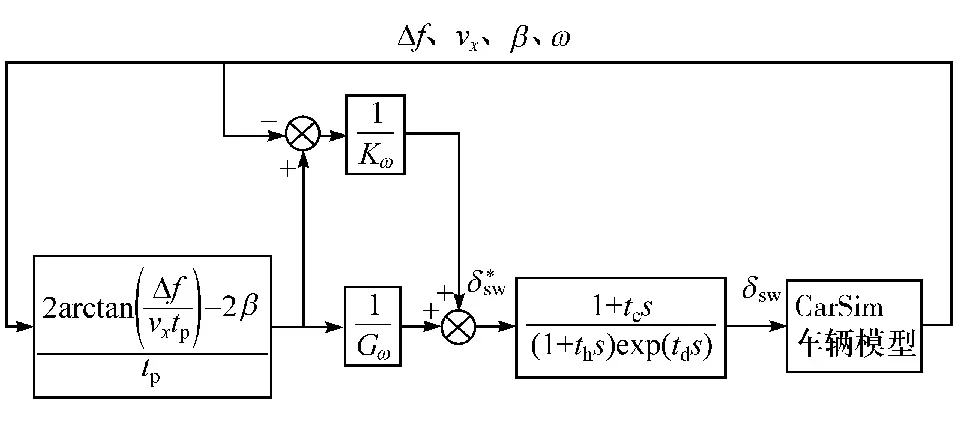
图2 驾驶员模型
图2 中,Δf为期望路径与实际路径横向偏差;vx、β、ω分别为车辆行驶速度、质心侧偏角和横摆角速度;tp、tc、th、td分别为驾驶员预瞄时间、微分校正时间常数、动作之后反应时间和神经反应滞后时间;Kω为反馈系数;Gω为车辆稳态增益,取Kω≈Gω,其表达式为
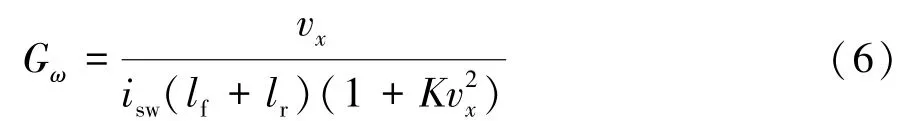
2.1.3 仿真工况设置
考虑到变道超车是无人驾驶车辆行驶过程中必须面对的一种驾驶工况,也是车辆行驶过程中易造成车辆失稳的典型工况,故仿真跟踪路径设置为双移线道路。 建立的参数化双移线道路如图3 所示。
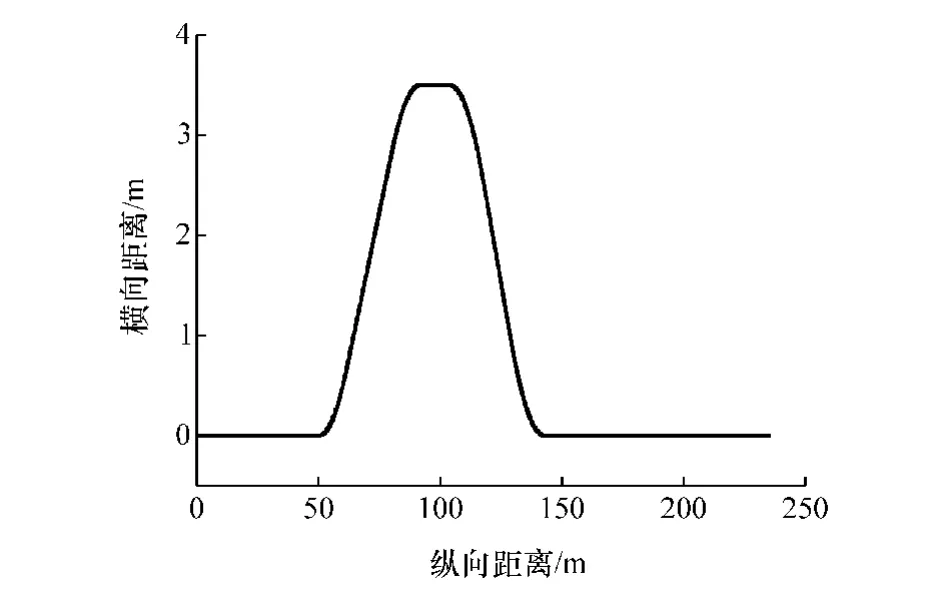
图3 参数化双移线道路
行驶速度为 60 ~100 km/h,步长为 5 km/h,匀速行驶,每组速度仿真时间为10 s,仿真频率为40 Hz,每组速度下仿真数据为400 组。
2.1.4 数据库建立
综合考虑车辆横向稳定性特征以及与车辆横向稳定性相关的行驶状态参数,选取横摆角速度ω、侧向加速度ay、质心侧偏角β、左前轮胎垂直载荷FZL1、右前轮胎垂直载荷FZR1、侧倾角ψ、侧向速度vy等7 个参数作为仿真输出参数。 CarSim 仿真输出参数为

由于轮胎垂直载荷和其他参数在数量级上差别较大,为避免异常值影响聚类精度,引入λ对其进行转换,转换公式为

最终得到用于聚类分析参数矩阵:
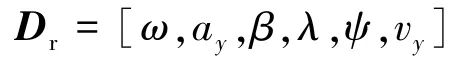
2.2 聚类分析
2.2.1 离线聚类分析
离线聚类的目的是对数据样本进行划分得到各类别聚类中心及其代表的稳定性等级。 根据车辆行驶特征,将车辆行驶状态分为稳定性行驶、趋向不稳定性行驶和不稳定性行驶3 个等级,即最终得到3个聚类中心,每个聚类中心代表一种车辆行驶稳定性状态。 各行驶状态对应的聚类中心等级如表2所示。
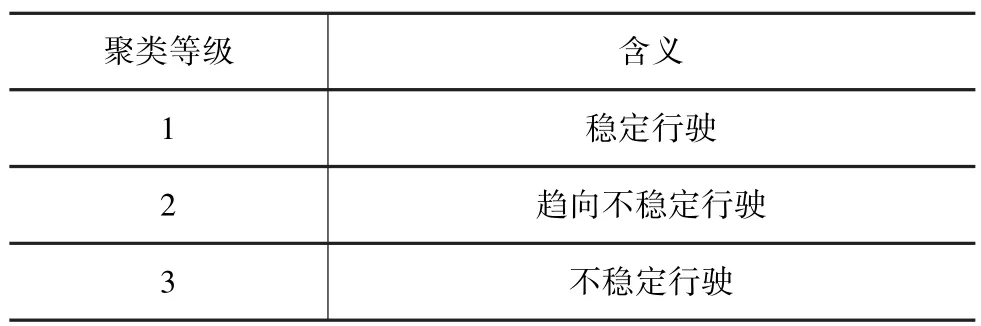
表2 聚类中心等级含义
利用Matlab 实现SOFM 神经网络算法,竞争层设置为1×3 个神经元,初始学习速率为0.02,训练次数分别设为 50、100、150、200、250 次,训练 200 次和训练250 次时的输出神经元权值(取绝对值)误差对比如表3 所示。
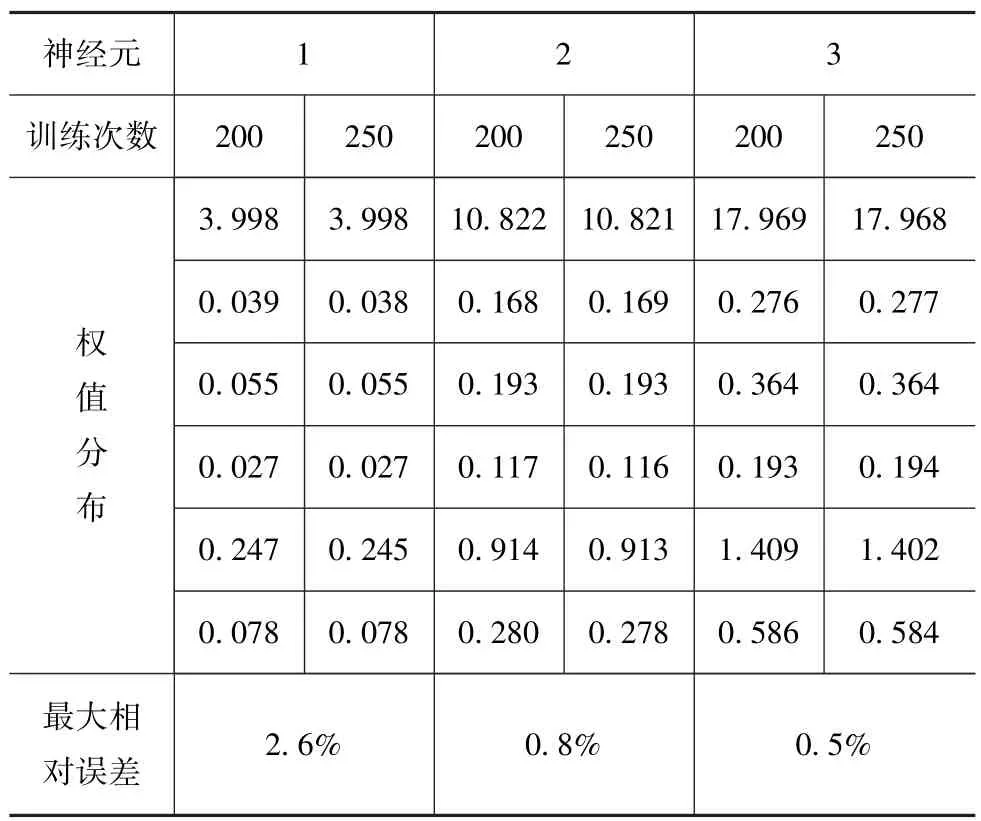
表3 训练200 次与训练250 次权值对比
由表3 可知,输出神经元权值基本相同,说明网络已经收敛,训练200 次时的竞争层神经元权值(取绝对值)如表4 所示。
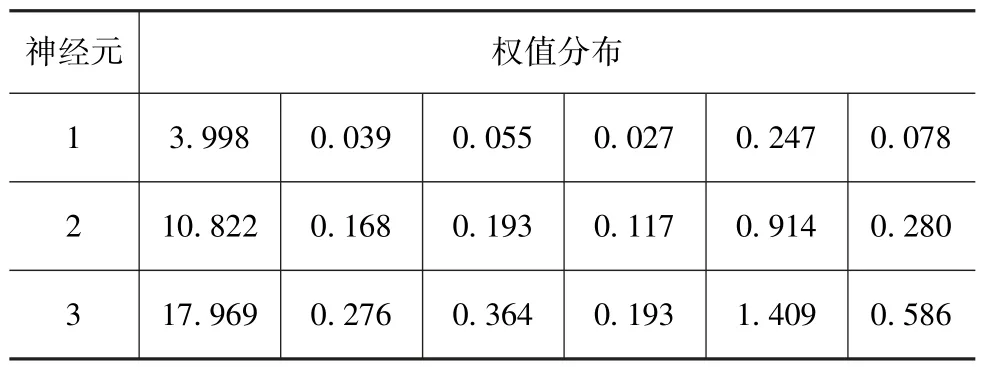
表4 各神经元权值
将训练200 次时竞争层各神经元权值作为K 均值聚类的初始中心进行进一步聚类分析,可以有效避免因初始中心选取不当影响聚类精度的问题。
无人驾驶车辆在不同速度下跟踪双移线路径,同一速度仿真时间为10 s,仿真时间共计90 s,利用K 均值聚类将车辆离线数据划分为3 种等级状态。聚类结果的精度,通过聚类中心偏移量的变化加以反映,如图4 所示。

图4 聚类中心偏移量变化曲线
由图4 可知,中心偏移量Δl随迭代步数增加一直减小,逐渐趋向于0,在第14 次迭代之后达到Δl=0,满足 Δl<0.0001 的聚类精度要求,聚类结束。 聚类结果如图5 所示。
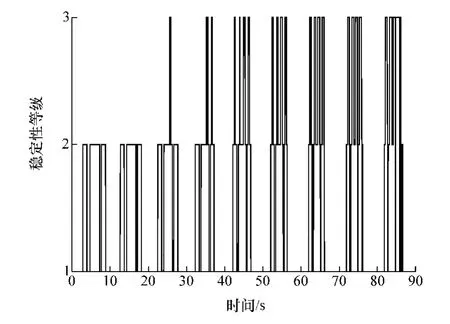
图5 离线聚类结果
由图5 可知,随着速度的增加,车辆跟踪双移线路径行驶过程中稳定性等级变动越大,高危险等级所占比例越高;同一速度下,驶入双移线道路前和驶出双移线道路后,车辆稳定性较高,而在进行换道跟踪行驶过程中,车辆稳定性降低。
分析图5 可知,基于组合聚类划分的车辆行驶稳定性等级与基于车辆行驶工况特点判别的结果基本一致。 各聚类等级对应的离线聚类中心(取绝对值)如表5 所示。
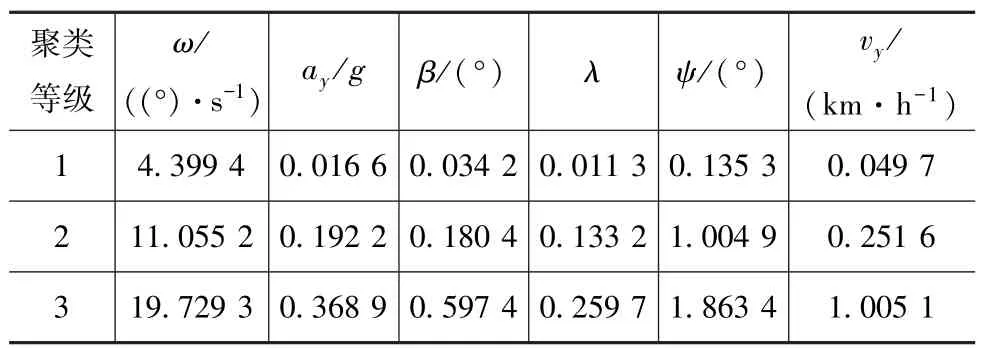
表5 聚类等级及其聚类中心
2.2.2 实时更新聚类中心
在线聚类分析的实质是基于聚类中心对车辆实时行驶参数进行类别划分,进而判别车辆当前的稳定状态。 无人驾驶车辆实际行驶工况复杂多变,而离线聚类得到的聚类中心是通过跟踪双移线道路提取的基础数据分析得到的,不具有一般性。 为提高组合聚类稳定性判别方法的鲁棒性和普适性,采用均值法对聚类中心进行更新:
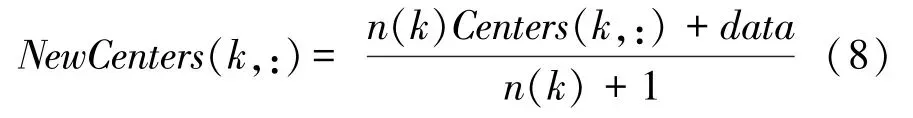
式中:NewCenters(k,:) 为更新后中心;k为聚类等级,k =1,2,3;data为车辆实时行驶参数;n(k) 为k类中样本数量。
2.2.3 在线聚类分析
在离线聚类基础上,通过实时更新聚类中心,计算车辆参数与各聚类中心的欧式距离,根据最小距离准则将实时数据样本赋给距离最近的聚类中心,对车辆行驶稳定性进行在线判别。 在线判别车辆稳定性原理如图6 所示。
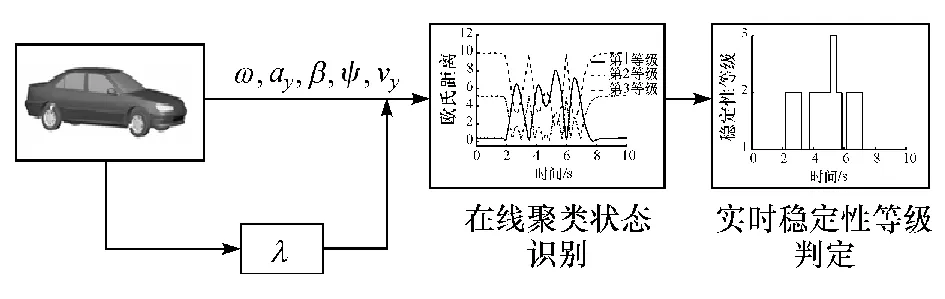
图6 在线判别原理
在线判别的仿真工况车速独立于离线聚类分析所包含的车速,本文中以车速为72 km/h 为例进行双移线路径跟踪的稳定性判别。 在线聚类得到的车辆实时行驶状态参数与各聚类中心间的欧氏距离如图7 所示。
由图7 可知,车辆在驶入双移线道路前和驶出双移线道路后,车辆行驶实时状态参数与第1 等级聚类中心欧式距离最小;当处于双移线道路换道行驶过程中,车辆逐渐趋向不稳定行驶,车辆实时行驶状态参数与各聚类中心间的最小距离在第2 等级和第3 等级间波动。
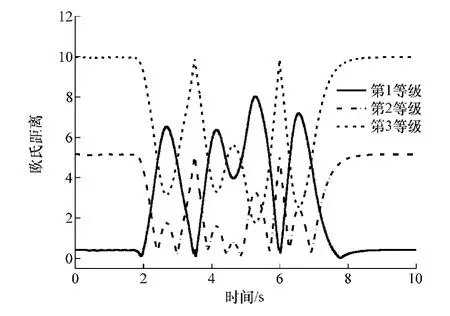
在线聚类得到的车辆实时稳定判别等级如图8所示。

图8 在线识别车辆稳定性等级
由图8 可知,车辆进行双移线路径跟踪过程中,车辆稳定性判别等级变化趋势为1→2→3→2→1,与根据车辆行驶工况的分析结果基本一致。
3 基于稳定性判别方法的稳定性控制
3.1 基准评价标准
以轮胎力法稳定性判据作为评价基准[15]对基于组合聚类的稳定性判别方法进行分析,联合工况下轮胎力的分布要符合附着椭圆[16],即车辆稳定行驶时,轮胎所受合力要在附着椭圆内。 通过式(9)建立近似附着椭圆,如图9 所示。 根据式(10)判断车轮是否达到附着极限,进而判断车辆行驶状态,定义车辆行驶状态如表6 所示。

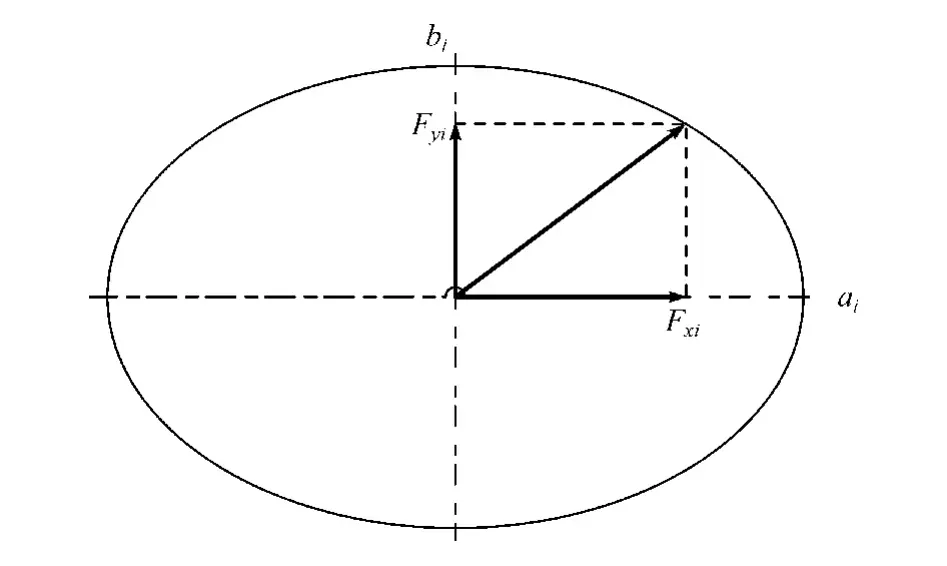
图9 轮胎力附着椭圆示意图

表6 轮胎力法稳定性判定
式中:ai =μFzi;bi =kiαi;i =FL,FR,RL,RR ;Fxi为纵向力;Fyi为侧向力;αi为侧偏角;μ为附着系数;ki为侧偏刚度。
利用CarSim/Simulink 搭建联合仿真平台进行多工况仿真分析。 图10 是车速为85 km/h、路面附着系数为0.8 时的双移线试验道路下车辆行驶稳定性判别情况的对比结果。
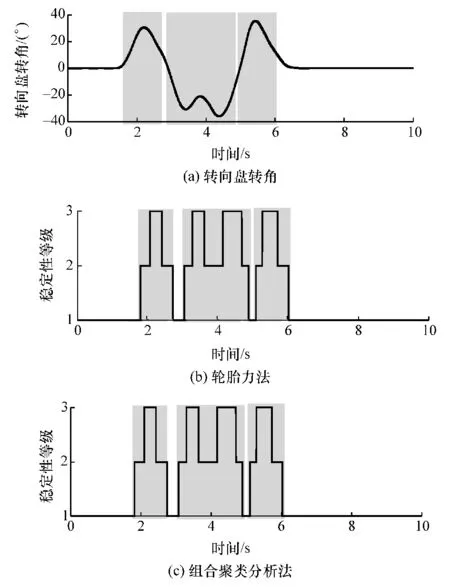
图10 双移线试验稳定性判定结果对比
由图10 可知,以轮胎力法判别结果为标准,车辆跟踪双移线路径行驶过程中出现3 个不稳定工况,分别出现在 1.8~2.7、3.1~4.8 和 5.1~6 s。
图11 是速度为85 km/h、路面附着系数为0.7时的鱼钩试验道路下车辆行驶稳定性判别情况对比。
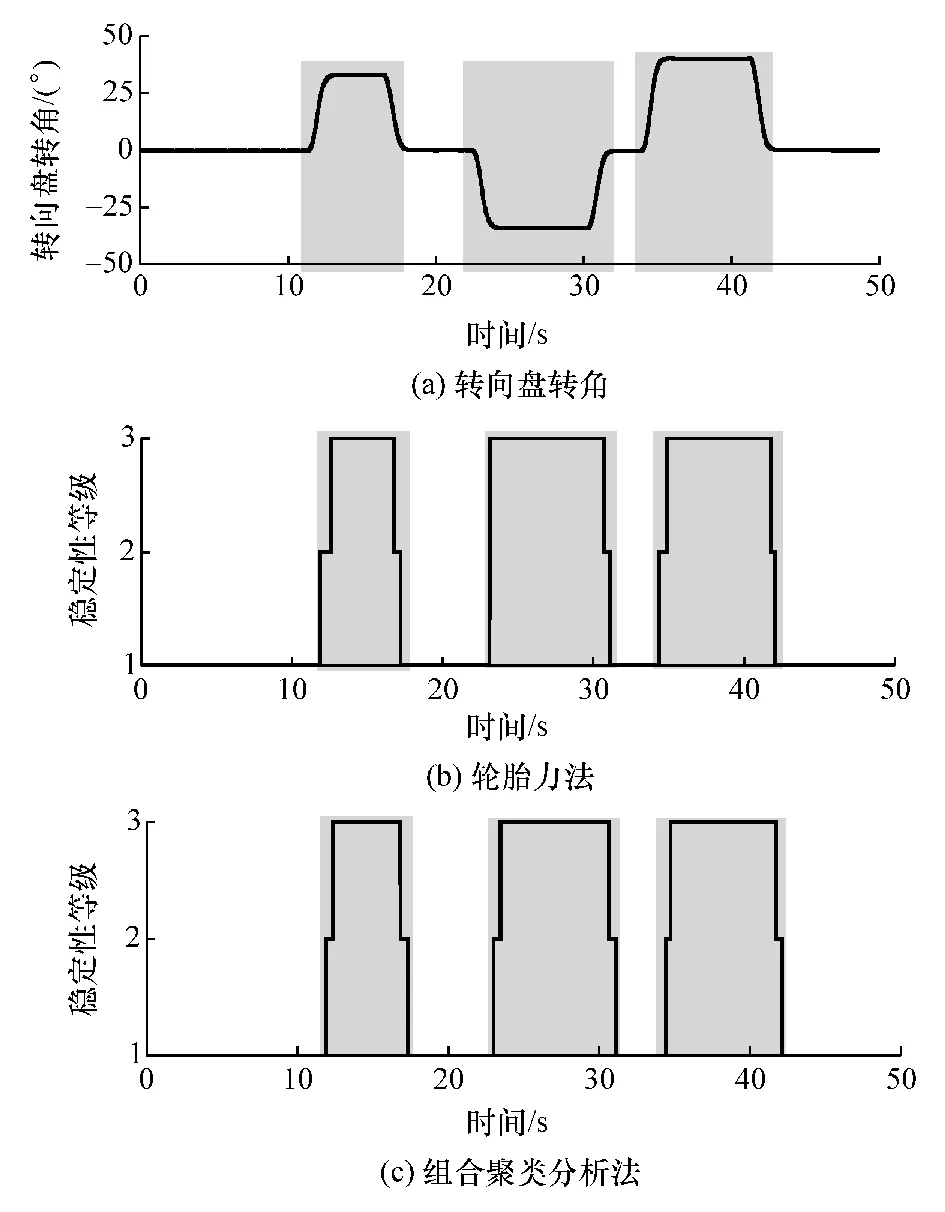
图11 鱼钩试验稳定性判定结果对比
由图11 可知,以轮胎力法判别结果为标准,车辆跟踪鱼钩路径行驶过程中出现3 个不稳定阶段,分别出现在 12.1 ~ 17.4、23.5 ~ 31.3 和 34.6 ~41.8 s。
分析图10 和图11 可知,车辆跟踪双移线道路和鱼钩道路行驶过程中均出现多次不稳定阶段,对比轮胎力法判别结果可以看出,基于组合聚类法对各不稳定阶段的判别都较准确,在出现和结束时刻上都与轮胎力法判别结果相差很小。
3.2 基于稳定性判别方法的稳定性控制仿真
将基于组合聚类的稳定性判别结果作为稳定性控制策略介入控制的依据,基于模糊控制理论设计稳定性控制策略,进行CarSim/Simulink 联合仿真分析。 仿真跟踪路径为双移线道路,双移线道路仿真工况是车速为85 km/h、路面附着系数为0.8,仿真对比结果如图12 所示。
由图12 分析可知:无人驾驶车辆在进行直道轨迹跟踪时,车辆对轨迹跟踪精度较高,同时车辆行驶较稳定;在进行弯道轨迹跟踪时,未施加控制的车辆对轨迹的跟踪精度降低,同时车辆稳定性出现波动。 图中黑色圆圈标记为控制策略介入控制时刻,控制策略是否介入控制由稳定性判别结果决定。 施加控制的车辆横摆加速度峰值为10.85°/s,相比于控制前下降了18.45%;车辆实际行驶轨迹与目标轨迹偏差峰值为0.373 m,相比于控制前下降了21.92%。
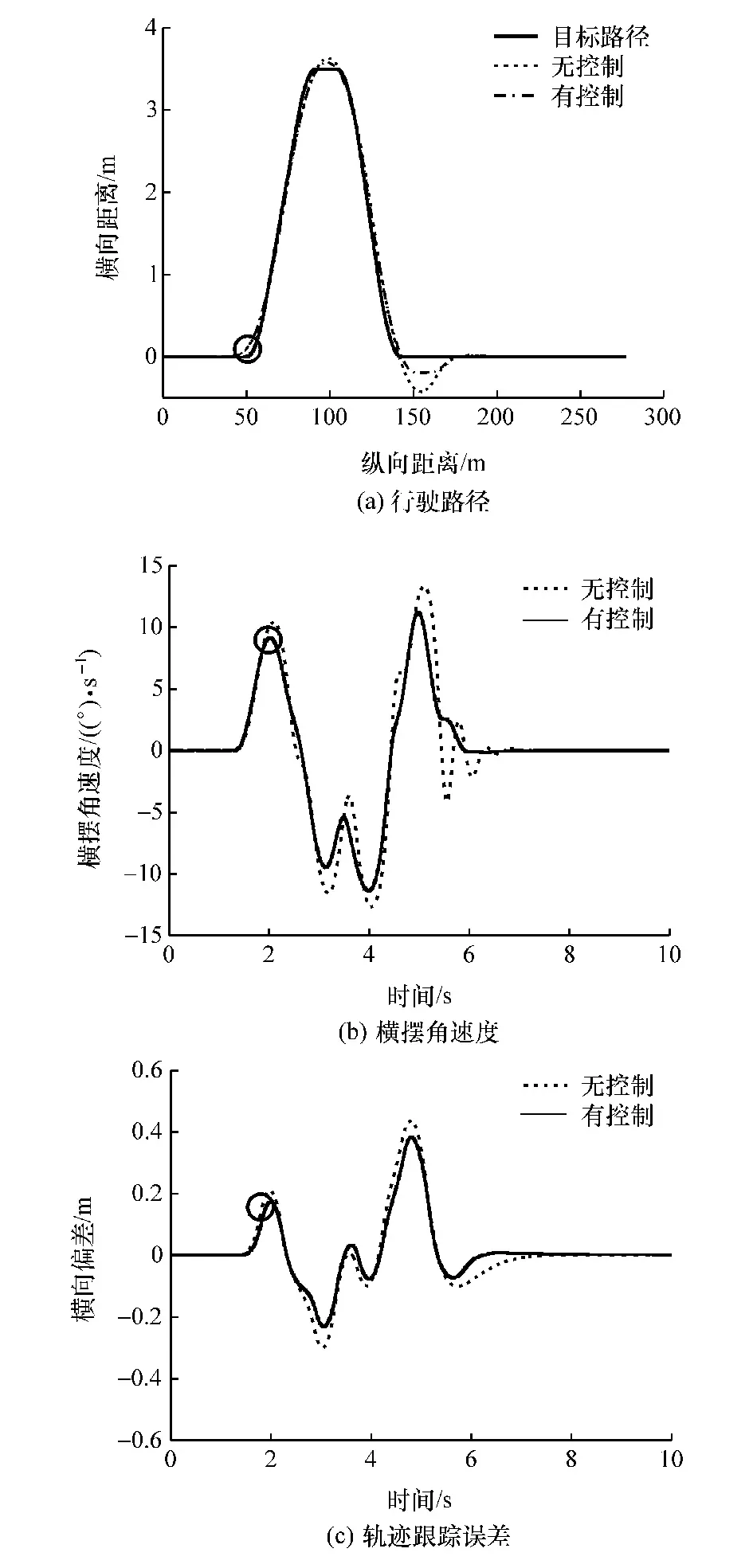
图12 双移线仿真结果
仿真结果表明,以基于组合聚类的稳定性判别结果作为稳定性控制策略介入控制的依据,在保证对目标轨迹跟踪精度的同时,提高了车辆稳定性。
3.3 基于驾驶模拟器硬件在环试验验证
为进一步验证基于组合聚类的稳定性判别方法的有效性和准确性,依托智能汽车实验室的驾驶模拟器进行硬件在环试验。 硬件在环试验平台由驾驶模拟器、上位机、仿真软件CarMaker 虚拟车-路模型及其感知系统、仿真软件平台NI VeriStand 和仿真硬件平台等组成,试验平台如图13 所示。

图13 硬件在环试验平台
图中装有Matlab 和Carmaker 的上位机与仿真硬件平台的NI 实时系统通过网线传递信号,驾驶模拟器中的控制器通过PXI-8510 板卡与NI 实时系统进行通信。
试验流程如下:Carmaker 中设置的车路模型、车辆状态等信息发送到NI 实时系统;在Simulink中设计的轨迹跟踪控制算法、组合聚类稳定性判别算法及稳定性控制策略编译后下载至NI 实时系统中的PXI-8840 实时处理器执行产生控制信号;NI实时系统将控制信号发送至驾驶模拟器中的执行器动作,执行机构输出信息通过PXI-8510 板卡发送给NI 实时系统,NI 实时系统将信号发送至Carmaker 控制车辆模型在虚拟道路上行驶,实现车辆稳定性控制硬件在环试验。 试验结果如图14所示。
仿真结果与硬件在环试验结果的对比如表7所示。
由图12、图14 和表7 可知,由于硬件在环试验存在一定的时滞性,导致仿真与试验结果有所不同,但据表7 中指标对比,仍可得出如下结论:在仿真和硬件在环试验中,以基于组合聚类的稳定性判别结果作为稳定性控制策略介入控制的依据,指导控制策略介入控制,均保证了车辆在跟踪目标轨迹精度的同时,提高了车辆稳定性,充分验证了该稳定性判别方法实时量化车辆稳定性的有效性和指导稳定性控制策略介入控制的准确性。
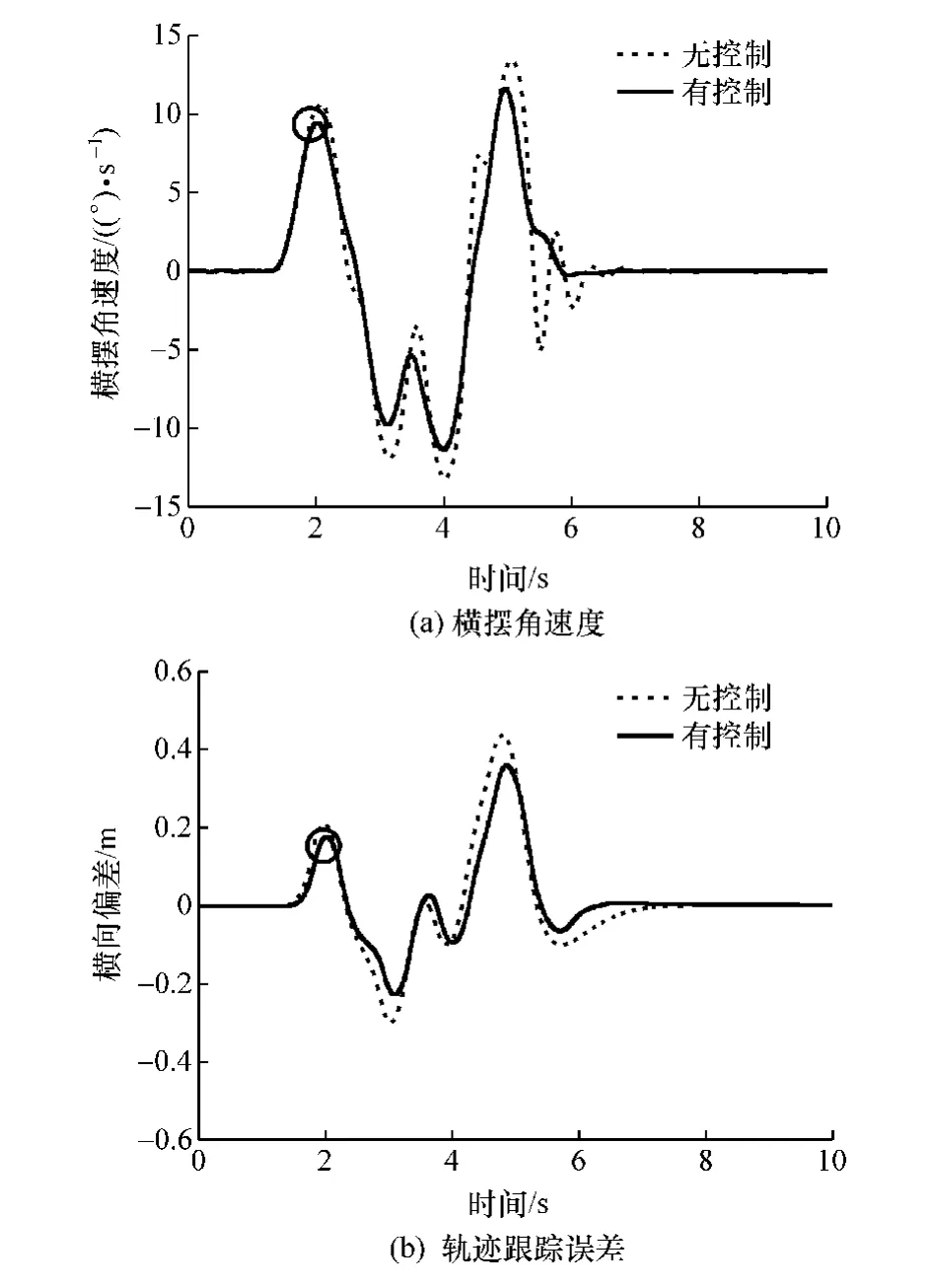
图14 试验结果
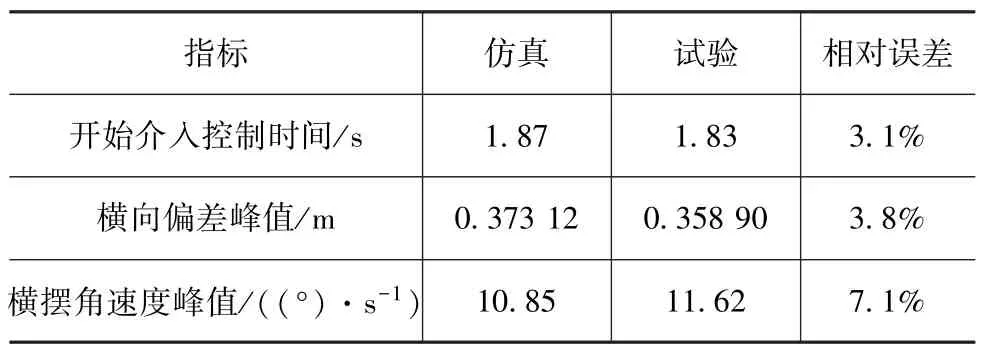
表7 仿真结果与试验结果对比
4 结论
(1)针对无人驾驶车辆行驶稳定性判别方法进行了详细研究,提出了一种利用SOFM 神经网络算法和K-means 聚类算法相结合的组合聚类法进行车辆横向稳定性判别。
(2)结合SOFM 神经网络算法和K-means 聚类算法各自的优缺点,对车辆行驶数据参数进行离线聚类分析,获得离线稳定性等级,并依据离线聚类结果对车辆稳定性进行在线判别,建立了基于组合聚类的稳定性判别方法。
(3)以轮胎力法为判别基准,对不同工况下基于组合聚类的稳定性判别方法得到的判别结果进行有效性分析。 分析表明,提出的基于组合聚类的稳定性判别方法运用在车辆稳定性判据构建上是有效的。
(4)仿真与试验结果表明,所提出的车辆横向稳定性判别方法能够实时量化车辆行驶稳定性和准确指导稳定性控制策略介入控制,提升无人车辆跟踪目标路径精度的同时,也保证了车辆的横向稳定性。
