机器人驾驶车辆深度强化学习换挡策略*
2020-12-08周楠,陈刚
周 楠,陈 刚
(南京理工大学机械工程学院,南京 210094)
前言
汽车的大量试验项目具有重复性强、持续时间长和操作要求精准等特点。 使用驾驶机器人进行试验可降低试验人员劳动强度,提高试验准确性。 目前,国外驾驶机器人关键技术处在保密阶段,只有少数发达国家拥有此项技术。 国内关于驾驶机器人的研究主要集中在东南大学、南京理工大学、中国汽车技术研究中心等几所高校和研究中心[1-4]。
换挡策略作为机器人驾驶车辆的关键技术之一,其合理性将直接影响机器人驾驶车辆的动力性、舒适性和燃油经济性等性能发挥[5]。 陈刚等[6]针对驾驶机器人建立了模糊神经网络换挡控制方法,利用模糊神经网络生成换挡策略,极大提高了机器人驾驶车辆换挡策略的性能。 目前机器人驾驶车辆换挡策略主要通过人为设定驾驶循环指令和拟合试验参数方法得到。 Miao 等[7]在两参数换挡策略的基础上引入道路坡度阻力系数,建立了含有道路坡度阻力系数的经济性换挡策略,提高了换挡策略对于环境的适应性,但它未考虑车辆加速度对换挡策略的影响。 陈清洪等[8]利用BP 神经网络和熟练驾驶员试验数据获得考虑了加速度的换挡策略,但该方法受驾驶员水平和样本数量与质量的影响较大。
建立换挡策略要重点考虑求解方法。 换挡策略的求解方法包括图解法、解析法、遗传算法和动态规划法等。 Zhu 等[9]采用解析法对经济性换挡策略进行了求解。 李浩等[10]在两参数换挡策略的基础上引入加速度作为换挡参数,实现了考虑加速度的动态三参数换挡。 但其求解过程中须针对各个油门开度求解加速度 速度曲线,求解复杂、计算量大。 利用解析法对换挡策略进行求解的优点是求解方法成熟,缺点是只能针对单一性能指标进行求解,且求解过程复杂、计算量大。 Yin 等[11]利用遗传算法对换挡策略进行了求解,提高了换挡策略的综合性能,解决了解析法只能求解单一性能指标的问题,但它也未考虑加速度对换挡策略的影响。 Ngo 等[12]利用动态规划方法在特定驾驶循环工况下,对不同动力储备系数下的换挡策略进行了求解。 Lei 等[13]以经济性为优化目标,通过动态规划算法对两参数换挡策略进行了求解。
动态规划在求解换挡规律时,须构建复杂的状态图,状态图复杂程度取决于动态规划算法中的离散程度。 过于复杂的状态图会因贝尔曼纬度灾难而出现收敛速度下降或无法收敛的情况。 为解决动态规划方法的贝尔曼纬度灾难问题,可采用深度神经网络强化学习算法对三参数换挡策略进行求解。 强化学习是一种通过对象和环境的交互对策略进行学习的方法。 相比动态规划算法,强化学习无须构建复杂的状态图,只须构建关于状态的转移函数[14]。薛金林等[15]通过强化学习神经网络对机器人驾驶车辆进行车速跟踪控制。 深度神经网络强化学习(DQN)算法是一种将蒙特卡罗思想和动态规划思想结合,并通过建立深度神经网络对价值函数进行近似的强化学习方法[16-18]。 DQN 算法可在无须对状态变量进行离散化的情况下,处理大状态空间或连续状态空间的动态规划问题。 因此,本文中采用DQN 算法求解机器人驾驶车辆三参数换挡策略。
首先建立了驾驶机器人车辆动力学模型和驾驶机器人换挡策略强化学习模型,并将油门踏板位置、车速和加速度作为换挡参数,将动力性作为学习目标。 然后通过训练,获得了驾驶机器人三参数最佳动力性换挡策略。 最后通过比较不同换挡策略验证了算法的有效性。
1 机器人驾驶车辆系统模型
1.1 驾驶机器人系统结构
驾驶机器人总体结构如图1 所示,主要由油门/制动/离合机械腿系统、换挡机械手系统、转向机械手系统3 个主要部分组成。 其中,油门、制动和离合机械腿能操控油门、制动和离合踏板。 换挡机械手与车辆换挡杆相连,在工作时通过与各个机械腿相配合完成对车辆的换挡操作。
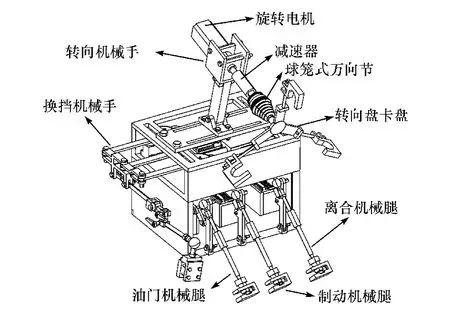
图1 驾驶机器人总体结构
换挡机械手是一个2 自由度七连杆并联结构,其机构模型如图2 所示,主要由3 部分组成,分别为箱体、直线驱动电机和换挡机械手机构。 在选挡过程中,挂挡摇杆保持不动,给选挡摇杆一个驱动转矩,通过其余各连杆的相互协调,即可通过手杆控制变速杆进行横向选挡工作。 在挂挡过程中,选挡摇杆保持不动,给挂挡摇杆一个驱动转矩,与选挡过程一样,通过其余连杆的相互协调,即可通过手杆进行纵向挂挡工作。
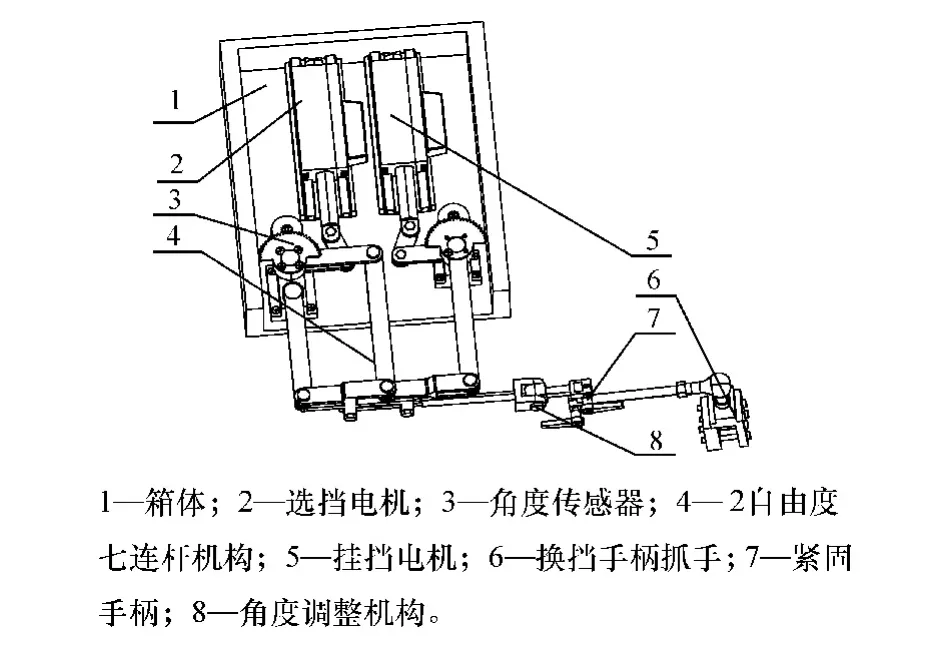
图2 换挡机械手结构模型
1.2 车辆动力系统模型
车辆在直线行驶时,主要受力包括驱动力、制动力、滚动阻力、坡度阻力和空气阻力。 简化的车辆纵向动力学模型可表示为
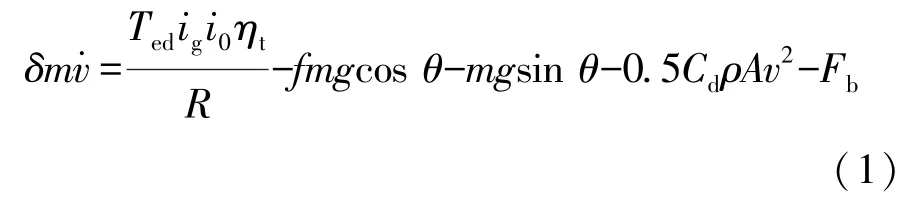
式中:δ为旋转质量换算系数;m为汽车总质量;为汽车行驶加速度;Ted为发动机动态输出转矩;ig为变速器传动比;i0为减速器传动比;ηt为传动系统效率;R为轮胎有效转动半径;f为汽车滚动阻力系数;θ为坡度角;Cd为空气阻力系数;A为汽车迎风面积;v为汽车行驶速度;Fb为制动力。
对于每个节气门开度αA,在稳定工况下所输出的转矩Te都是关于发动机角速度ωe的函数:

式中:αA为节气门开度;ωe为发动机角速度。 发动机稳态输出转矩Te是与发动机角速度ωe和节气门开度αA相关的非线性函数,一般用发动机试验得到的发动机MAP 图表示。
由于发动机大部分情况在非稳态工况下工作,采用修正系数对发动机稳态工况下的输出转矩进行修正,并将其作为非稳态下的输出转矩[19]。 发动机动态输出转矩为

式中:为发动机曲轴角加速度;φ为非稳态工况下发动机输出转矩下降系数,取值为0.03。
1.3 机械腿运动学模型
驾驶机器人中,油门机械腿、制动机械腿和离合机械腿具有相同的结构,建立机械腿电机输出位移到踏板位移之间的运动学模型,如图3 所示。
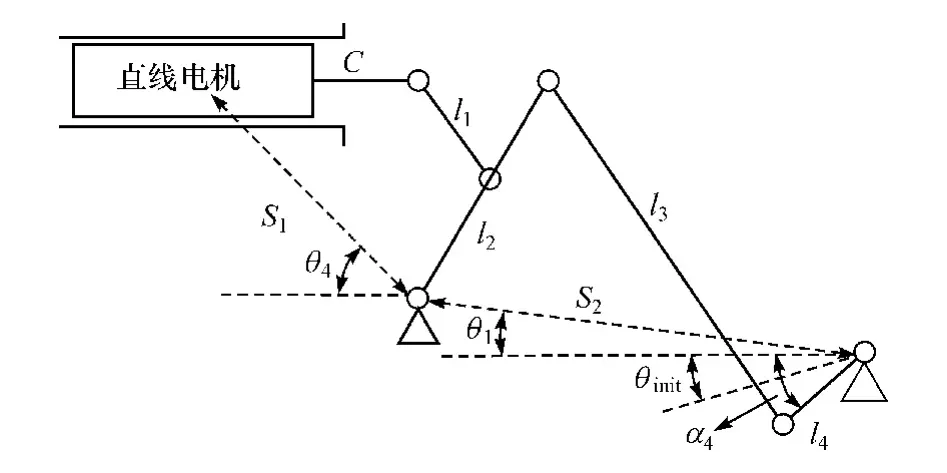
图3 机械腿运动学模型
机械腿运动学方程为
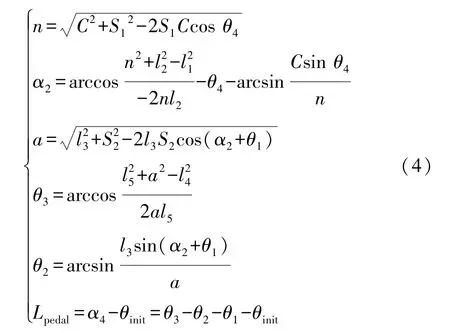
式中:S1、S2、θ1~θ4均为已知的驾驶机器人安装参数;C为直线电机推杆总长;l1~l5为机械腿结构参数;θinit为踏板初始位置与水平线之间的夹角;α4为踏板实际位置与水平线之间的夹角;Lpedal为踏板角位移。
驾驶机器人油门机械腿控制的是油门踏板位移,它决定了油门开度。 首先通过机器人驾驶车辆性能自学习方法[20]获得油门踏板初始位置和极限位置对应的油门机械腿直线电机输出位移。 除去踏板空行程阶段,油门踏板位移和油门开度可简化成线性模型。 因此,可通过油门机械腿直线电机输出位移使α4变化,而得到油门开度αA。
对于离合器踏板,须建立离合器踏板位移与压板升程之间的传递过程。 离合器行程传递分为两个部分,一是踏板位移到分离轴承行程之间的传递,二是分离轴承行程与压盘升程之间的传递。 踏板位移与分离轴承行程之间的传递公式为

式中:LRB为分离轴承行程;Lpedal为踏板位移;iRS为分离系统杠杆比。
分离轴承升程与压盘升程之间的行程传递公式为

式中:LC为离合器压盘升程;iclutch为离合器杠杆比。
由式(4)~式(6)可以得到离合器系统行程传递公式:

1.4 换挡机械手运动学模型
驾驶机器人换挡机械手结构模型如图4 所示,由3 条开链组成,分别是手杆O1BP、选挡摇杆O2DC和挂挡摇杆O3EC。

图4 换挡机械手结构简图
已知选挡摇杆和挂挡摇杆的输入角度θ31和θ21,则C点坐标为
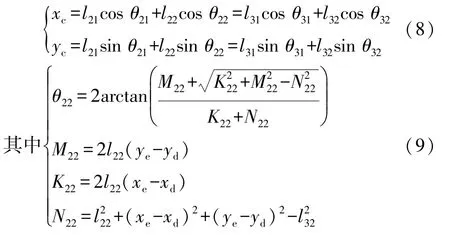
求解出C点坐标后,通过手杆求解出θ11和θ12。

式中:l11~l32为各杆长度;θ11~θ32为各杆与水平线之间的夹角;(xc,yc)为C点坐标;(xd,yd)为D点坐标;(xe,ye)为E点坐标。
2 机器人驾驶车辆深度强化学习换挡策略
机器人驾驶车辆深度强化学习换挡策略如图5所示。 它包括了机器人驾驶车辆换挡策略强化学习模型和换挡策略求解两部分。 机器人驾驶车辆换挡策略强化学习模型由驾驶机器人模型和车辆模型组成,并通过马尔可夫决策过程进行描述,建立了模型相关的状态空间、动作空间和奖惩机制。 而其换挡策略求解则采用深度神经网络强化学习(DQN)算法。 驾驶机器人采集车辆行驶状态并根据奖惩机制计算奖励,将采集到的车辆行驶状态、挡位、奖励保存在经验池中,DQN 算法单步提取经验池中部分经验对预测Q网络和目标Q网络分别进行更新。 在学习过程中,通过贪心算法根据预测Q网络选择挡位。

图5 机器人驾驶车辆深度强化学习换挡策略框图
2.1 机器人驾驶车辆换挡策略强化学习模型
马尔科夫决策过程来描述机器人驾驶车辆换挡策略强化学习模型。 马尔科夫决策过程<S,A,T,R>, 即系统下一时刻的状态由当前时刻的状态决定,不依赖于以往的任何状态。
S是状态空间,表示车辆行驶状态变量的集合。状态变量s为车辆行驶状态,包括车速v、油门开度αA、行驶加速度,假设车辆在一次换挡前后保持油门开度不变。 状态空间为:S={v,αA,}。 车辆在t时刻的状态s(t)={v(t),αA(t),(t)}。
A是动作空间,表示车辆所能采取的动作变量的集合。 动作变量a为所能选择的挡位,动作空间A={1,2,3,4,5},车辆在t时刻选择的动作(即挡位)为a(t)∈A。
T是状态转移函数,用于描述下一时刻状态s(t+1)和当前状态s(t)间的关系。 状态转移函数由驾驶机器人模型和车辆模型决定。 机器人驾驶车辆换挡策略强化学习模型从状态s(t)开始,采取动作a,根据状态转移函数T状态s(t)转移到下一个时刻状态s(t+1),表示为

式中:ig(t)为在t时刻挡位对应的传动比;v(t+1)和v(t)分别为t+1 和t时刻的车速;Te(t)为发动机输出转矩;Fb(t)为t时刻的制动力;α(t+1)和α(t)分别为t+1 和t时刻的节气门开度;(t+1)为t+1 时刻的汽车行驶加速度;β=fcosθ+sinθ。
R是奖惩机制,是根据学习目标为强化学习方法提供奖励的函数。 本文中学习目标为动力性换挡策略,描述为车辆在舒适度约束条件下以最短时间t达到当前油门下所能达到的最高车速vmax。 其计算公式为
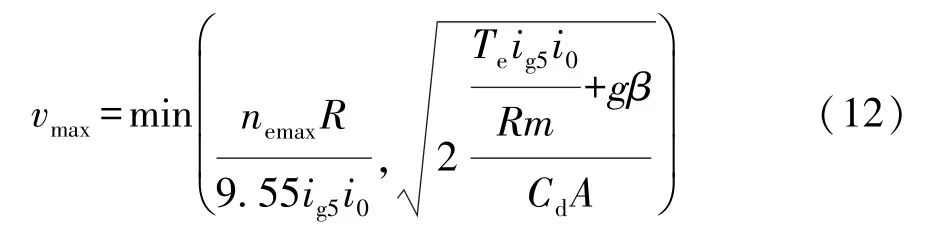
式中:nemax为发动机设定的最高转速;ig5为最高挡位的传动比。
通过最大化折扣累计奖励值的形式描述学习目标,最大化折扣累计奖励值为
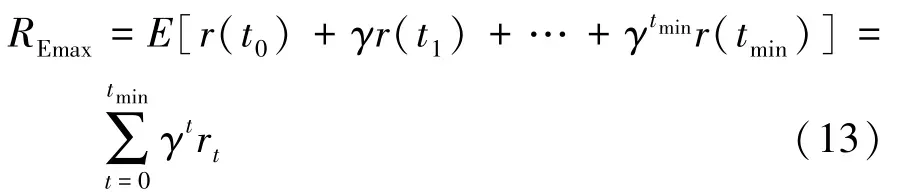
式中:γ为奖励递减值,取值在区间[0,1]内,表示未来奖励对当前状态的影响程度;rt是在t步时获得的奖励。 根据学习目标将奖惩机制分为3 个部分。
第1 部分为终止奖励,用于奖励车辆到达终止状态,即车辆到达最高车速vmax时的状态。 此时奖励为10。
第2 部分为在执行一次换挡动作后无法满足舒适性条件下的惩罚。 利用冲击度来反面表示舒适程度,冲击度定义为

本文中设定换挡过程中最大冲击度Jmax的绝对值不超过10 m/s3,当冲击度大于最大冲击度Jmax时,奖励设为-10。
第3 部分为临时奖励,临时奖励是关于换挡后到达车速相关的函数。 临时奖励是对驾驶机器人进行一次换挡动作的奖励,作用是提高学习效率。 临时奖励rt计算公式为

根据式(14)和式(15)可得奖惩机制:
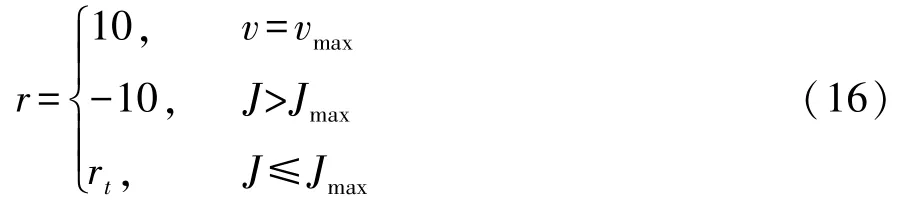
2.2 机器人驾驶车辆换挡策略求解
使用DQN 算法对驾驶机器人动力性换挡策略进行求解。 驾驶机器人在车辆行驶状态s下根据换挡策略π选择挡位G,挡位的选择表示为

动作价值函数Q(s,a)是对折扣累计奖励值的估计,是机器人驾驶车辆在车辆行驶状态s下选择挡位G后,根据换挡策略π继续行驶后得到的期望折扣累计奖励值(又称为Q值)。 在车辆行驶状态s下对应挡位G的Q值越大,说明挡位G可以得到更多的折扣累计奖励值。 动作价值函数表示为
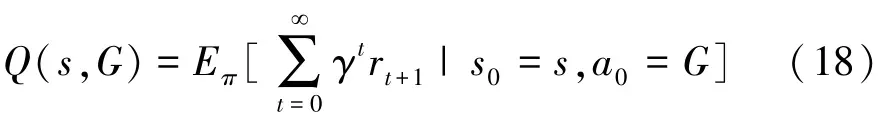
式中:s0为车辆起始行驶状态;a0为车辆起始行驶状态下采取的第一个挡位。
换挡策略π表示当前车辆行驶状态下对应Q值最大的挡位G,换挡策略π表示:

对于换挡策略来说,其状态空间是高维且连续的。 利用神经网络对动作价值函数进行近似表达,所采用的神经网络结构如图6 所示。
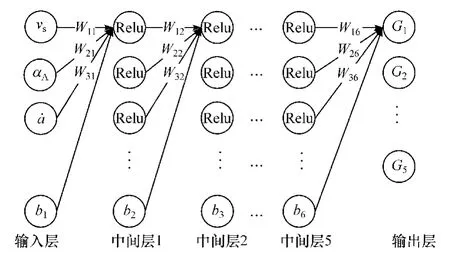
图6 神经网络结构
神经网络有5 个全连接层作为中间层,采用线性整流函数(Relu)作为神经网络激活函数。 线性整流函数表示为

式中:W为神经网络的权重;b为神经网络的偏秩。
每个全连接层包括11 个节点。 数据输入为车辆状态数据(车速、油门开度和加速度)。 输出层输出的是所有挡位对应的Q值。 近似后的动作价值函数为

式中λ为神经网络参数。
通过神经网络对动作价值函数进行近似化表达,换挡策略π表示为
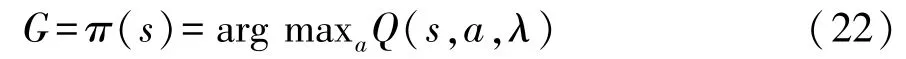
在求解换挡策略时,通过使用两个结构相同、参数不同的全连接神经网络(称为预测Q网络和目标Q网络)来完成对换挡策略π的更新。 目标Q网络生成车辆行驶状态s下所有挡位的Q值,作为预测Q网络的标签。 预测Q网络利用奖惩机制和目标Q网络提供的Q值来更新自身参数。 目标Q网络的更新则是在经过一定次数的迭代后,将预测Q网络中的参数λ复制给目标Q网络。 通过迭代最终得到最优的换挡策略。
在学习过程中,采用e-贪心算法来选择挡位。在挡位选择时,以1-e的概率选择当前换挡策略下的最优动作 arg maxaQ(s,a,λ)。 以e的概率从所有动作中均匀随机选取一个。 通过e-贪心算法可以避免最终得到的换挡策略是局部最优。 贪心算法表示为

为提高计算效率,利用经验池存储历史经验。通过随机抽取历史经验进行学习。 采用随机抽样的方法可降低不同历史经验的相关性,以提高神经网络的更新效率。
预测Q网络的更新通过将预测Q值和目标Q值的差值平方作为损失函数,反向传递更新预测Q网络参数,损失函数表达为
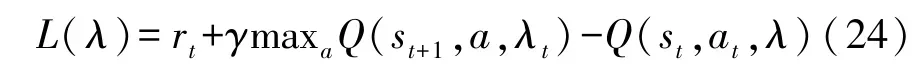
式中 maxaQ(st+1,a,λt)为目标Q网络以st+1为输入时输出的最大Q值。
完成一次更新后的预测Q网络为
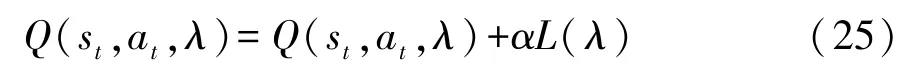
通过不断的学习对预测Q网络和目标Q网络中的参数进行更新,直至收敛,得到最优的换挡策略:
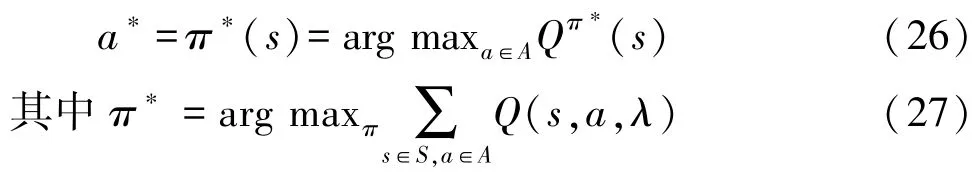
降挡延迟通过引入方法改进获得,收敛系数的公式为

式中:vn为一定油门开度下n挡升入n+1 挡的车速;vn+1为一定油门开度下n+1 挡降到n挡的车速。
根据经验获得收敛系数A,如表1 所示。

表1 不同油门开度下的收敛系数
3 仿真与试验
为了验证所提出换挡策略的动力性,进行了驾驶机器人车辆加速性能仿真。 仿真中,驾驶机器人车辆分别采用提出的换挡策略和用解析法求解的双参数换挡策略进行了固定油门加速。 其中,提出的换挡策略是通过训练获得的,获得的策略是关于车速、油门开度、加速度的三参数换挡策略。 生成此换挡策略时,所采用的算法参数如表2 所示,车型参数如表3 所示。 训练过程中误差变化曲线如图7 所示。
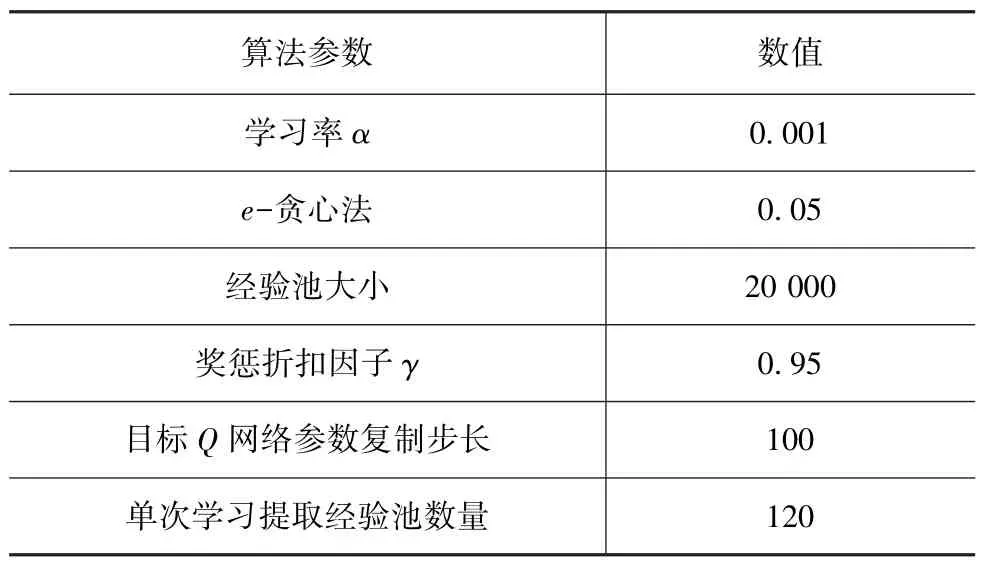
表2 算法参数

表3 车型参数
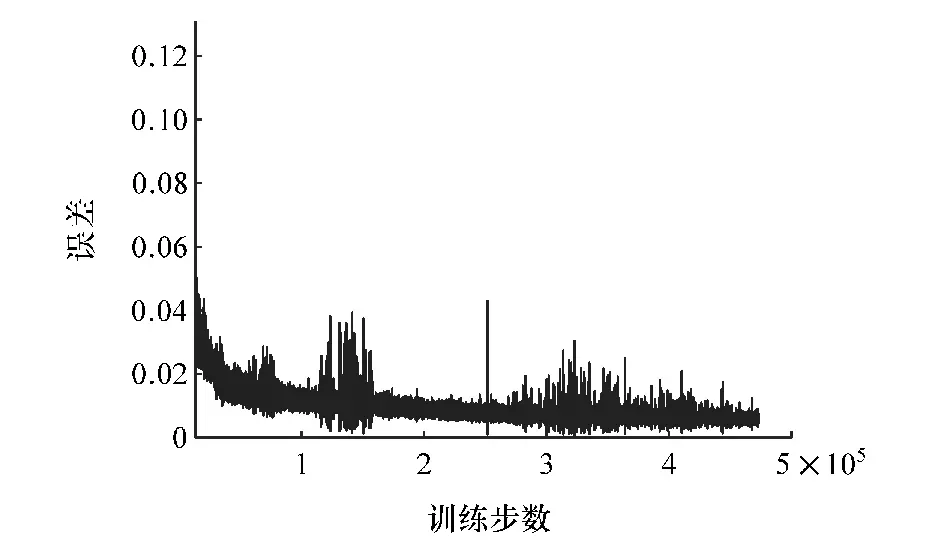
图7 训练过程中误差变化曲线
由图7 可见,训练误差是收敛的。 在训练过程中,训练误差随着训练步数的增加不断减小,最后趋于0。 图中的误差波动是目标Q网络参数更新造成的。
将采用解析法求解的两参数换挡策略和训练获得的提出换挡策略进行35%固定油门开度加速的对比,曲线如图8 所示。
由图8(a)可以看出,10 s 加速时间内,利用解析法求解的换挡策略从0 加速至61.18 km/h,通过本文方法求解的换挡策略加速至62.17 km/h,提升0.99 km/h。 机器人驾驶车辆的加速性能得到改善。由图8(b)可以看出,驾驶机器人在相同油门开度下10 s 内行驶路程由358 m 增加到371 m,提升13 m。说明通过本文中提出的求解换挡策略可以使驾驶机器人更好地发挥车辆的动力性能。 由图8(c)和图8(d)可以看出,驾驶机器人使用本文求解换挡策略时,更倾向于在高车速/转速换挡,以提高动力性能。从图8(f)可以看出,本文中求解出的换挡策略在冲击度规定范围内满足舒适性要求。

图8 固定油门加速的对比曲线
为进一步验证提出的换挡策略的有效性,进行了机器人驾驶车辆驾驶循环试验。 根据相关标准[21],BOCO NJ 150/80 型底盘测功机上,由驾驶机器人对试验车辆进行驾驶循环试验。 车速控制方法采用PID 控制。 机器人驾驶车辆的驾驶循环试验现场如图9 所示。 在试验过程中,实时采集驾驶机器人油门机械腿、试验车辆车速和换挡机械手的实时数据。

图9 机器人驾驶车辆驾驶循环试验现场图
采用提出的换挡策略和模糊神经网络(FNN)换挡策略分别进行驾驶循环试验,对比曲线如图10 所示。 从图10(a)可以看出,利用本文方法求解换挡策略和FNN 求解换挡策略都可以很好地完成驾驶循环试验。 由图10(b)可以看出,驾驶机器人控制最大油门开度57%下降至16%,一次驾驶循环试验平均油门开度由4.13%下降至4.06%,使用本文方法求解换挡策略能以更低的油门开度完成驾驶循环试验。 由图10(e)可以看出,利用本文求解换挡策略,冲击度绝对值由FNN 求解换挡策略的16.21 下降到6.01 m/s3。 通过本文方法求解换挡策略可以在提高车辆动力性的同时改善舒适性。
4 结论
提出了一种基于深度神经网络强化学习算法的机器人驾驶车辆三参数换挡策略。 首先建立了机器人驾驶车辆的动力学模型,包括了车辆纵向动力学模型、机械腿运动学模型和换挡机械手运动学模型。通过将机器人驾驶车辆动力学模型转化为机器人驾驶车辆强化学习模型,车速、油门开度、行驶加速度作为状态变量,机器人驾驶车辆所能选择的挡位作为动作变量,以车辆在舒适度约束条件下用最短时间到达最高车速为学习目标,建立奖惩机制,奖惩机制分为终止奖励、惩罚和临时奖励。 利用深度神经网络强化学习算法(DQN)求解三参数换挡策略,通过使用两个结构完全相同但参数不同的全连接神经网络(预测Q网络和目标Q网络)完成对换挡策略的更新。 目标Q网络对换挡策略下的折扣累计奖励值进行估计并作为预测Q网络的标签,预测Q网络利用目标Q网络提供标签和奖惩机制,对自身参数进行更新。 通过多回合训练得到机器人驾驶车辆的动力性换挡策略。

图10 驾驶机器人驾驶循环试验对比
试验与仿真结果表明,基于深度强化学习求解出的三参数换挡策略提高了无人机器人驾驶车辆的动力性能,10 s 加速试验速度由61.18 km/h 提升至62.17 km/h,10 s 内路程长度增加 13 m。 通过速度跟踪试验,基于深度强化学习求解出的三参数换挡策略比模糊神经网络换挡策略在无人机器人驾驶车辆上表现出更好的动力性能,同时改善了舒适性。再一次验证了换挡策略的准确性。
但在建模过程中,未考虑实际模型参数的变化和外部干扰对建模带来的误差,尤其是换挡机械手、离合机械腿受负载波动时的影响和车辆中不同踏板的踏板特性。 在换挡策略中未将安装驾驶机器人前后车身质量的变化考虑进去。 这些将作为接下来的研究工作。
