非线性Pochhammer-Chree方程解的研究
2020-12-05邱立军江苏联合职业技术学院盐城机电分院江苏盐城224000
邱立军(江苏联合职业技术学院盐城机电分院,江苏盐城 224000)
1 引言
微分方程在科学研究和工程应用中得到广泛的使用,可以通过方程的解来描述不同的现象结果,但由于微分方程的计算过程中往往会忽视大部分有用的信息,从而导致不能准确描述实际现象,例如弹力力学[1].而非线性方程则可以通过偏微分与误差估计等方式求出精确解,在流体力学、空间离子等领域具有重大的应用[2,3].例如,在非压缩或接近条件下,描述弹性杆的纵向形变波传播可用非线性的Pochhammer-Chree方程(非线性P-C方程)表示为utt-uttxx-当p=3或5时,它表示了质点两种不同结构[1].特别当p=3时,即

表示的纵向形变孤立波相互作用是非弹性的.此外,求非线性方程的精确解也逐渐出现许多方法,如(G′/G)方法、F-展开法、齐次平衡法、反散射方法、EXP-函数法等等[4-8].EXP-函数法已经被广泛应用于求解非线性发展方程.本文通过运用EXP-函数法求解方程(1),包括孤波解、周期解,从而丰富了EXP-函数法在求解非线性方程的精确解中的应用.
2 EXP-函数法求解的方法简述
EXP-函数法求解非线性偏微分方程的一般步骤如下:考虑非线性偏微分方程

其中x,t为变量,u为因变量.为了求方程(2)的行波解,作变换

其中c为待定常数.将式(3)代入方程(2)中,可将(2)式化为一个常微分方程

假设方程(2)的解 u(ξ)可以表示为 exp(ξ)的有限幂级数,即
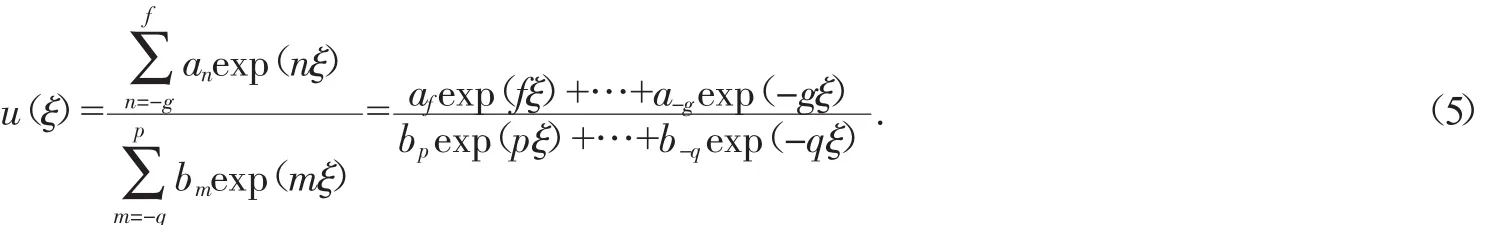
其中f,g,p,q是待定正整数;an,bm是待定常数.为了确定f和p的关系,平衡方程(4)的非线性项和最高阶偏导数项的最高次;同理平衡方程(4)的非线性项和最高阶偏导数项的最低次,便得到g和q的关系.再把f和p,g和q取一些特殊值,就可以将方程(4)的左边化为 exp(nξ)的多项式.再令含 exp(nξ)(其中 n=0,±1,±2,…)项的系数为零,得到相应的一组代数方程组,应用数学软件Maple求解这个代数方程组,可求出待定系数an,bm(n,m=0,±1,±2,…).将这些结果代入式(5)便得到方程(2)用exp(nξ)表示的行波解的一般形式.
3 非线性Pochhammer-Chree方程的精确解
利用EXP-函数法求解方程(1)的精确解,将式(3)代入方程(1)得到下列常微分方程

设方程(6)的解可以表示为式(5)的形式,则为了确定 f,g,p,q 之间的关系,首先平衡(6)式中 u(4)和 u2u″的最高次,由(5)式可得

其中 Ai是常数,比较(7)和(8)式,令 f+5p=3f+3p,得 p=f.
再平衡(6)式中 u(4)和 u2u″的最低次,由(5)式可得

其中 Bi是常数,比较(9)和(10)式,令 -(g+5q)=-(3g+3q),得 g=q.
3.1 情形Ⅰ
令 p=f=1,q=g=1,则由(5)式,得

其中 ai,bi为待定常数.将(11)式代入方程(6),并利用 Maple计算得到



3.2 情形Ⅱ

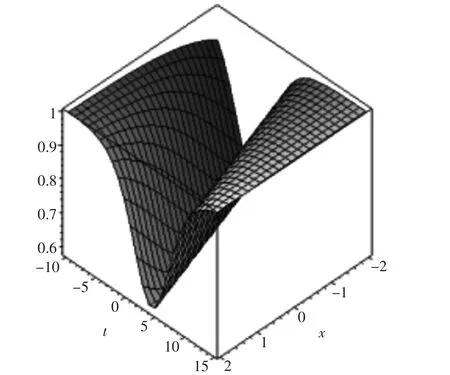
图1 两双曲函数解u23的波形图(其中 c=0.5,-10≤t≤15,-2≤x≤2)

图2 两双曲函数解u23的波形图(其中 c=1.5,-6≤t≤2,-6≤x≤2)


图3 两双曲函数解u29的波形图(其中 3≤t≤9,-9≤x≤15)
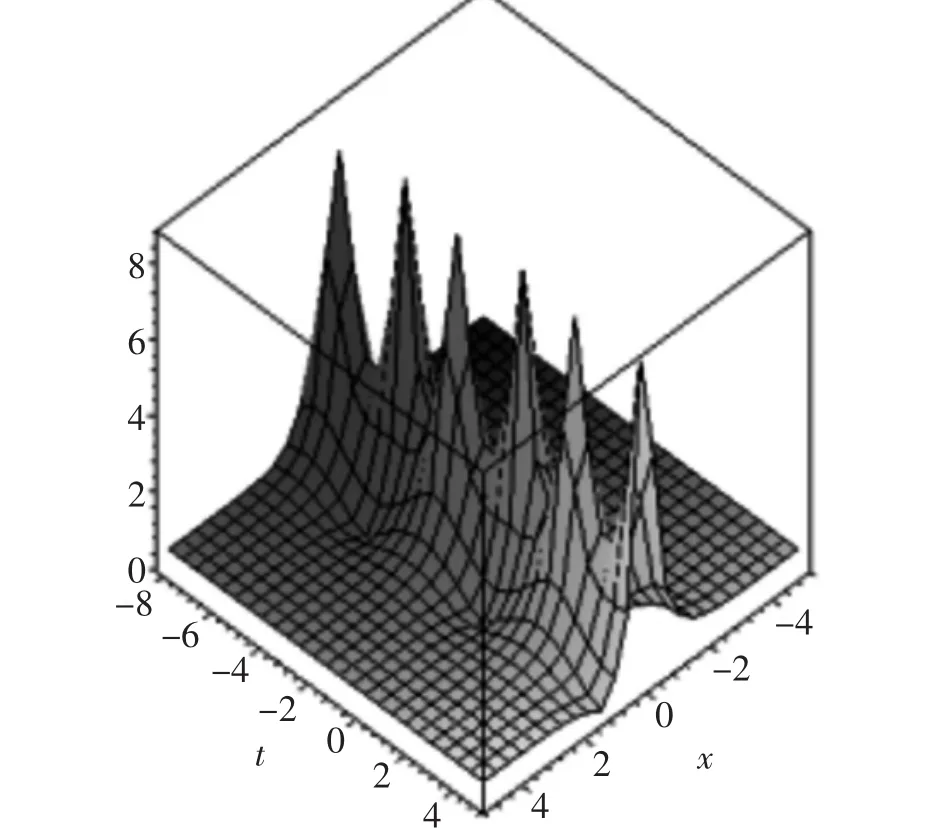
图4 两双曲函数解u45的波形图(其中 a2=0.5,-8≤t≤5,-5≤x≤5)

当参数 b0满足(54)时,解(51)为两个孤立波解

3.3 情形Ⅲ
令 p=f=3,q=g=3,则由(5)式,得


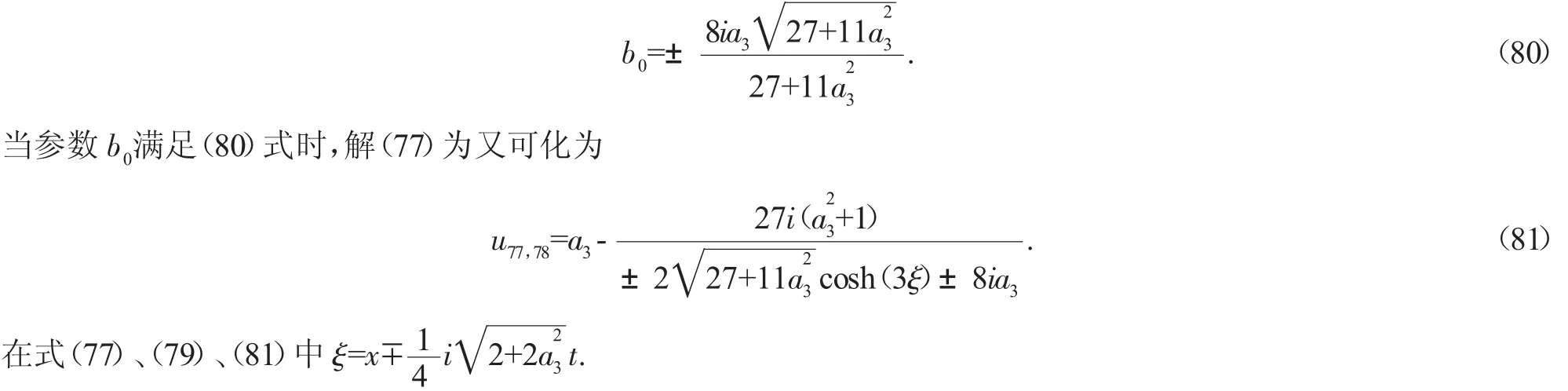
4 结论
利用EXP-函数法结合齐次平衡法原理,并借助数学软件再次研究了p=3时的非线性Pochhammer-Chree方程.本文首先求出了方程的指数函数解,再将其中一些参数取特殊值,就可以把指数函数解化为双曲函数解.通过比较,解(42)、(43)、(68)、(69)的结构与文献[1]、[4]中的解的结构相同;同时还出现了大量与现有文献中解的结构不相同的解,表明本文不仅进一步证明了文献中精确解的有效性,而且丰富了相关文献中解的类型.
