正弦型波纹管二次流强化换热模拟研究

江嘉铭，吴文杰，黄淑龙，刘义保，张国书，王合义

（1.东华理工大学核资源与环境国家重点实验室，江西 南昌 330013；2.东华理工大学核科学与工程学院，江西 南昌 330013；3.东华理工大学人工智能学院，江西 南昌 330013）

换热器是一种常见的核电厂安全设备，同时在化工、能源、制冷、冶金等众多领域都有广泛应用[1]，强化换热器的换热能力一直都是国内外学者的重点研究方向。波纹管是一种基于强化传热技术提出的异型结构换热管道，其管道壁面由多组相切的圆弧构成，具有换热效率高、热补偿能力强、不易结垢等诸多优点[2-4]。因此，需要对波纹管展开数值模拟分析，进一步探究结构参数对波纹管换热能力及流动特性的影响。

目前，国内外有关波纹管的研究成果丰富，极大地推进了波纹管强化换热技术的发展。曾敏等[5]对不同管径波纹管内的层流流动和换热特性进行了研究，得到了波纹管强化换热的临界雷诺数（Re）；Sun[6]等人对不同波纹管的湍流动力学和强化传热机理进行了研究，分析了波纹管的结构参数对流体流动、传热及压降的影响；肖金花[7]、Pethkool[8]、Wang[9]等人分别对大小圆弧相切的波纹管、螺旋型波纹管以及波纹-直管交错的波纹管进行了研究，得到了各类波纹管强化换热的较优结构参数。何小平等[10]利用Fluent软件对正弦波纹管的流动和传热进行了二维模拟，分析了正弦波纹管增强传热的方法；陈瑶等[11]基于FLuent软件对不同正弦波纹管的1/4模型内流体进行了数值模拟分析，分析了其与当量直管的努塞尔数（Nu）之比，找出了正弦波纹管的传热效果最佳的流体状态参数。赵虎城等[12]从场协同理论的角度分析流体在正弦波纹管内的流动与传热的情况，分析了速度场与温度梯度场之间的协同关系。

然而，国内外大多数学者没有对正弦波纹管内流体与换热特性进行全模型的数值模拟，也未对正弦波纹管的二次流[13]展开研究。因此，在国内外丰富的研究基础上，依据计算流体力学基础理论，对不同结构的正弦波纹管开展全模型三维数值模拟，分析二次流强化波纹管换热规律具有重要意义。

1 数学模型

采用不可压缩均质流体，密度为常数，稳态流动，根据波纹管的结构尺寸与流体的基本参数，可知流体在波纹管的流动为湍流。在模拟过程中，流体满足能量守恒、质量守恒以及动量守恒，其基本方程如下[14-16]。

连续性方程：

动量守恒方程：

能量守恒方程：

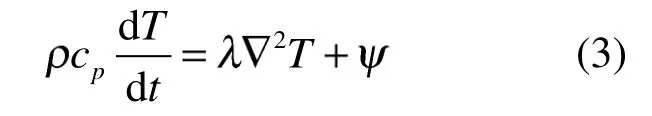
式中：u为管内流体的平均速度，m/s；p为管内流体运行压力，Pa；为流体的运动黏性系数，m2/s；为流体的密度，kg/m3；cp为流体的定压比热容，J/(kg·K)；T为流体的温度，K；为流体的热导率，W/(m·K)；为流体的摩擦热速率，W。

采用RNGk-ε湍流模型方程[17]模拟二次流：

式中：k为流体湍动能；为流体的湍流耗散率；有效黏性系数，Cμ=0.084 5；Gk为由平均速度梯度引起的湍动能；Gb是由浮力影响引起的湍动能；YM为可压缩湍流脉动膨胀对总的耗散率的影响；ak和aɛ分别为湍动能k和耗散率的有效湍流普朗特数（Pr）的倒数，1.39，。

RNGk-湍流模型的参数模型方程如下：

式中Sij为方程以柱坐标表达的曲线项。

2 计算模型与模拟条件

2.1 模型结构参数

本文选择的波纹管为工业领域常见的正弦型波纹管，即波形满足

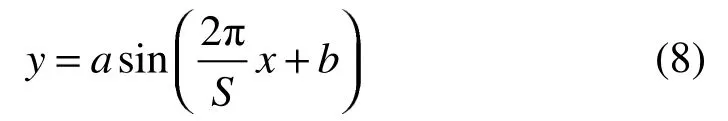
式中：a为波纹的波峰高，mm；S为正弦波纹管的周期，mm；b为波纹沿水平轴的平移距离，mm，本文所用的波纹起始点为原点，b=0。

为使流体在计算域内充分发展，波纹段取10个周期s。同时，为了避免进/出口流体的影响，两侧各设置40 mm长的直管段，波纹管结构如图1所示。

图1 波纹管结构Fig.1 The structure sketch of sinusoidal corrugated tubes

5个正弦型波纹管C1、C2、C3、C4和C5的结构参数见表1。 其中，C1、C2和C3模型的波峰高a一致，波纹周期S逐渐增大；而C1、C4和C5模型的波纹周期S一致，波峰高a逐渐增大。此外，增加了当量直径的光滑直管C0模型作为参照。

表1 管道结构参数Tab.1 The structural parameters of the tubes

2.2 边界条件设置

为了对5种结构的波纹管及光滑直管进行分析，对其主要边界条件设定如下：1）管内工质为液态水，入口温度20 ℃，入口Re分别为2 000、3 000、5 000、10 000、20 000，管内压力为标准大气压；2）换热采用第一类边界条件，即在波纹段壁面加载60 ℃的恒温条件。

2.3 网格无关性验证

网格无关性验证是确保模拟计算结果精度的必要过程。网格划分采用非结构化四面体网格，并对壁面边界处网格进行加密。

以C1模型为验证模型，对其离散为50万、100万和150万3种数量的有限元模型，同时，在入口Re为2 000的工况下进行模拟，其模拟计算结果见表2。

表2 网格无关性验证Tab.2 The grid independent verification

由表2可见，网格数量为100万和150万时，波纹管出口温度的模拟结果相对偏差仅为0.5%。综合考虑模拟精度及计算机性能后，选择100万的网格模型，具体网格划分如图2所示。

图2 网格划分Fig.2 The mesh generation

3 模拟结果与理论值对比分析

为了进一步分析模拟结果可信度，采用理论经验公式Gnielinski[18]对光滑直管进行理论与数值模拟的对比分析。

式中：Nu为流体努塞尔数；Re为流体雷诺数；Pr为流体普朗特数；f为流体流动阻力系数。

流体在流动过程中的阻力系数f可由Filonenko公式[19]计算获得

分别对小、中、高3种Re下，光滑直管Nu的理论与数值模拟结果进行了对比，结果如图3所示。从图3可以看出，当Re处于中等以下时，Nu的理论值与模拟值具有非常好的重叠度，模拟数据与理论经验公式计算数据吻合较好，最大偏差仅为12.4%，表明该数值模拟结果的误差在可接受的范围[20]内。

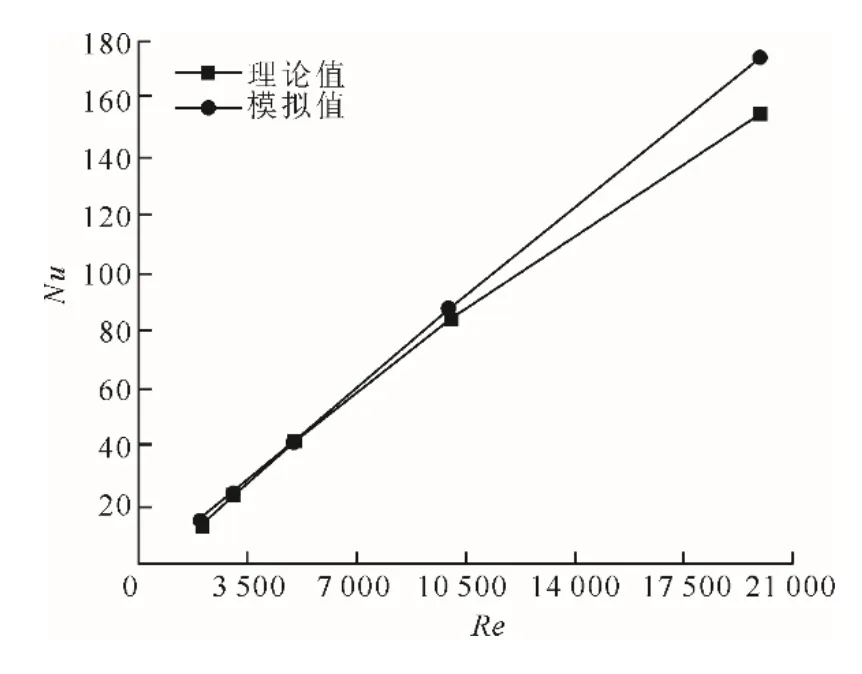
图3 光滑直管的数值模拟结果与理论计算结果对比Fig.3 The numerical simulation results and theoretical calculation results for the smooth straight tube

在分析该模拟方法误差可信的基础上，对光滑直管C0和波纹管C1的Nu随Re变化的趋势进行了对比分析，结果如图4所示。

图4 光滑直管与波纹管的Nu随Re变化关系Fig.4 The changes of Nusselt number of the smooth straight tube and corrugated tube with Reynolds number

从图4可以看出，2种换热管的Nu都随着Re的增大而增大，但波纹管的Nu曲线一直位于当量直径的光滑直管之上，说明波纹管的Nu在所有工况下都高于光滑直管。

当入口流速为3 m/s，正弦型波纹管的流速等值线如图5所示。从图5可以看出：随着正弦型波纹管的a/S减小（如表1，a不变），波纹管波峰壁面的速度在不断降低，而C2与C3波峰壁面流速近似相等，说明波纹周期S对波峰壁面流速呈负关系；随着正弦型波纹管的a/S增大（如表1，S不变），波纹管波峰壁面的速度在不断升高，说明波峰高a对波峰壁面流速呈正关系。在相同流速下，正弦型波纹管的流线如图6所示。从图6可以看出：自左至右，流体在正弦型波纹管的第一个波峰处的二次流涡线几乎没有；随着正弦波纹管的a/S减小（如表1，a不变），流线在波峰处的涡线减少，说明波纹周期S增大，正弦型波纹管波峰处的二次流涡线逐渐减少，波纹管周期S越大，正弦波纹管的二次流越弱。然而，从图5还可以看出，随着正弦型波纹管的a/S增大（如表1，S不变），流线在波峰处的涡线增多，说明波峰高a增大，正弦型波纹管波峰处的二次流涡线逐渐增多，波纹管波峰高a越大，正弦波纹管的二次流越强。

图5 正弦波纹管速度等值线Fig.5 The velocity contour map of the sinusoidal corrugated tube

图6 正弦波纹管流线Fig.6 The streamlines of the sinusoidal corrugated tube

因此，正弦型波纹管内流体在波峰处有明显的流线二次涡流，减小了边界层的厚度，同时也增加了流体的湍流程度，从而强化了换热。同时，当a/S≥0.15时，正弦型波纹管波峰处二次流涡线增多增密。

3个正弦型波纹管Nu随Re的变化曲线如图7所示。由图7可以看出，3条曲线的差距较小，其中C1曲线位于另两条曲线上方，表明具有较小波纹周期的正弦波纹管换热性能最好，波纹周期越小，波纹出现的频率越大，加剧了正弦型波纹管内流体的扰动程度。但相比于管道长度，波纹周期的变化幅度较小，对波纹周期的影响不明显，所以C1、C2和C3波纹管的Nu差距较小。

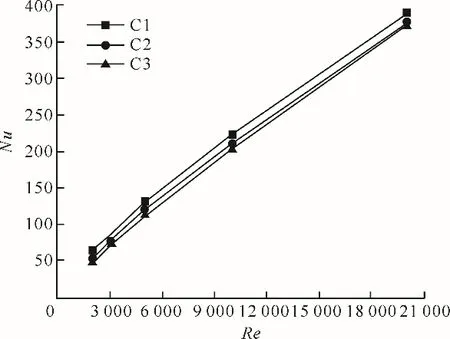
图7 不同波纹周期的波纹管Nu随Re变化关系Fig.7 Relationship between Nusselt number and Reynolds number of the corrugated tube with different wave periods

不同波峰的3个波纹管的Nu随Re变化曲线如图8所示。由图8可以看出：当Re小于3 000后，通过改变波峰以强化正弦型波纹管换热的效果并不明显；而当Re大于3 000后，波峰越高，Nu越大。这表明通过改变波峰以强化正弦波纹的换热更适用于Re大于3 000的工况，波峰越高的正弦型波纹管的换热性能越好。

图8 不同波峰高的波纹管Nu随Re变化关系Fig.8 Relationship between Nusselt number and Reynolds number of the corrugated tube with different wave heights

各个正弦型波纹管的流动阻力系数f随入口Re的变化曲线如图9所示。由图9可以看出：整体来看，f随着Re的增加而降低，且波纹管的流动阻力小于光滑直管；同时，f随着波纹周期的缩小和波峰高的增加而减小；具有较小波纹周期和较大波峰高的波纹管相对紧凑，流体在其管内的流速变化更剧烈，平均Re较高。

图9 各个管道的f随Re变化关系Fig.9 Relationship between f and Re of each tube

为了综合评价正弦型波纹管的换热性能，引入传热强化比η作为评价标准：

式中：Nu为正弦型波纹管的换热努塞尔数；Nu0为同等工况、同等管径下光滑直管的换热努塞尔数。

各个波纹管的η随入口Re的变化情况如图10所示。从图10可以看出：整体来看，η随着Re的增加而降低；具有较小波纹周期和较大波峰高的波纹管η更高；通过改变波纹周期，在湍流条件下，最高可使波纹管强化传热效果达到光滑直管的约4.1倍，改变波峰高最高可达到约4.5倍的强化效果，比其他类似结构的波纹管[21]性能稍有提高。

图10 各波纹管的η随Re变化关系Fig.10 Relationship between η and Re of each corrugated tube

4 结 论

1）波纹管的特殊结构能使流体在垂直于轴的方向上产生二次流，提高流体的湍流程度，强化管道的换热能力，当Re大于3 000后，波峰越高，Nu越大，正弦型波纹管的换热性能越好。

2）具有较小波纹周期和较大波峰高的波纹管换热能力更强。在相同条件下通过改变波纹周期，最高可使波纹管强化传热效果达到光滑直管的约4.1倍，改变波峰高最高可达到约4.5倍的强化效果。

3）流动阻力系数随着波纹周期的缩小和波峰高的增加而减小。因此，在实际工程应用中通过合理调整波纹周期和波峰高在一定程度上能降低波纹管的流动阻力。