基于DOE与梯度优化的驱动条件多参数分析与优化
2020-12-04陈雪凯
路 昕 盛 誉 陈雪凯
(核工业理化工程研究院,中国 天津 300180)
0 引言
在离心力的作用下,转子内部的气体沿径向的分布随着半径的平方近似呈指数型分布,实现了双组分气体沿径向的分离。
为了进一步的提高效率,在转子内部附加一个轴向的二次环流,使得径向的分离效果得到倍增。根据转子内环流产生的原因,大致将外驱动方式分为:热驱动、支臂机械驱动和供取料驱动。热驱动是指由于气体温度不均所产生的环流驱动方式,又可以分为:端盖热驱动和侧壁热驱动。前者通过控制上下端的温差来产生环流,后者通过控制侧壁温度的分布来产生环流。机械驱动是指转子的机械部件(例如转子内的静止支臂)与气体相互作用,所产生环流的驱动方式。供取料驱动在转子内部是十分复杂的一种驱动方式。目前存在的一种供取料方式是:在中心轴线附近供料,在两端通过支臂取料。
合理匹配多种驱动条件实现分离效果的优化,以及明确各个驱动条件对分离效果的影响特性是当前分离理论研究的重点。
本文以驱动条件多参数优化为切入点,在分离理论计算的基础上,引入DOE与梯度优化算法联用得多参数优化算法[1-3],并探索多参数对物理性能响应的关键性和交互性。
1 物理性能计算方法
1.1 物理模型和参数

图1 计算模型
采用二维轴对称模型,转子的轴向高度为H,半径为ra,角速度为ω。引入内边界的条件,计算区域为连续流区。同时,采用以下环流驱动条件:
(1)温度驱动:上、下两端温度均匀分布,分别为T上端和T下端。侧壁温度分为等温与线性两种。线性温度分布时,侧壁两端与转子两端温度相同,分布呈线性。 等温温度分布时,T侧壁=(T上端+T下端)/2。
(2)机械驱动:用旋转速度滞后于转子速度的无限薄圆盘模拟取料支臂对气体的机械驱动作用,支臂附近的气体旋转角速度为(1+β)ω,-1<β<0。
(3)供取料驱动:不考虑供料气流离开供料装置后的具体行为,认为供料气流到达内边界处是一股具有一定宽度的、可以看成连续介质的流体,供料流量为F。上、下两端采用环形狭缝模拟取料作用,分流比为θ。
1.2 计算方法
采用微扰理论对Navier-Stokes方程组进行简化,把轴向环流作为小扰动叠加到等温刚体旋转状态上,并选择等温刚体旋转状态的物理参量作为特征量对方程进行无量纲化处理。各物理量可以看作两种运动分量的叠加,代入方程,略去二次及高阶项,得到柱坐标系下、无量纲化、线性化运动基本方程为:


其中,r,z为径向,轴向坐标;u,w,v为径向、轴向和角向的速度;p,T,ρ分别为气体压力、温度和密度;ε0=exp (Ar2),A=Mω2r2a/2RT0,T0为 平 均 温 度 ,Br=μ/ρ0ω2r2a/κT0是 Brinkman 数 ,E=μ/ρ0ωr2a是 轴 线 处 的Ekman数,ρ0为侧壁密度,M为分子量,R为普适气体常数,μ和κ分别为气体黏性系数和热传导系数。
在得到转子内部流场分布后,采用低丰度条件下的改进径向平均法求解转子内部的丰度分布,进而得到物理性能。
2 DOE分析与梯度优化算法联用优化
DOE(试验设计,Design of Experiment)有三个步骤:试验计划、执行试验和结果分析,其中结果分析包括:试验数据表格、散点图、ANOVA分析表、Pareto图、主效应图、交互效应图、相关性图等。
计算选取的试验设计方法为最优拉丁超立方方法。以两因子9水平为例,拉丁超立方设计仅需9个试验点就可以完成空间的填充。最优拉丁超立方设计改进了随机拉丁超立方设计,可以使所有的试验点尽量均匀地分布在设计空间,具有非常好的空间填充性和均衡性。

表1 驱动条件参数取值表
梯度优化算法能够利用函数的导数、梯度等数学特征,实现高效的优化。寻优过程可以近似表达为:首先选定初始点X(0),按某个方向S(0),以初选步长 α(0)寻找一个新点X(1),使函数值f增加,并重复这一过程,直到获得最优解X*,即:X(k+1)=X(k)+α(k)S(k)确定序列;满足f(X1)<f(X2)<…<f(Xk)<f(Xk+1)<…;直到f(X*)⇒max。
DOE与梯度优化算法联用:应用DOE分析在设计空间中均匀采样,捕捉整个设计空间中最有效的设计区域。然后应用梯度优化算法在有效设计区域中进行优化设计,最终可获得最佳设计结果。该方法可以在更少的优化次数下得到更优的结果。

图2 拉丁超立方设计
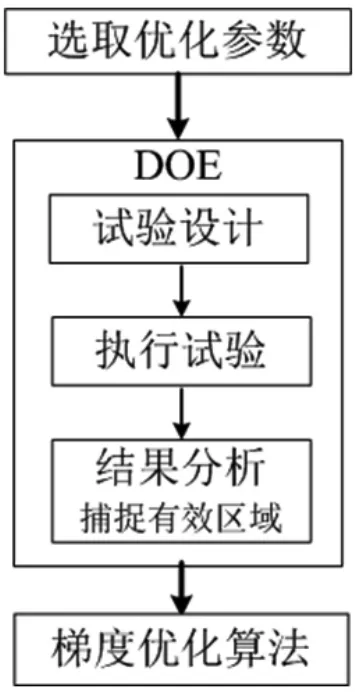
图3 DOE与梯度优化算法联用流程
3 驱动条件的多参数分析
3.1 关键因子分析
DOE分析的后处理功能根据样本点建立针对物理性能的多元二次回归模型,并通过对系数进行归一化处理转化为贡献度的百分比,建立Pareto图。图中带条纹的表示正效应,无条纹的表示负效应。图4为驱动条件对物理性能影响的前10项所建立的pareto图。结果显示,三种驱动条件中热驱动的影响仍然占主导作用。

图4 驱动条件对物理性能影响的Pareto图
3.2 主效应及交互性分析
主效应图表示因子在每个水平,其他因子的所有可能的组合对结果的影响的平均值。交互效应图根据主效应分析的结果,反映某两个因子的交互性对响应的关系和程度。其是在第二个因子取不同水平的情况下,分别作出第一个因子对响应的主效应图,然后叠加而成。两条曲线不平行的程度反映了交互效应的强弱。

表2 优化结果
如图5和图6所示,热驱动条件和机械驱动条件的两条曲线交叉,是强交互关系;热驱动条件和供料流量的两条曲线没有明显交叉,是弱交互关系。可见,三种驱动条件间存在交互关系。
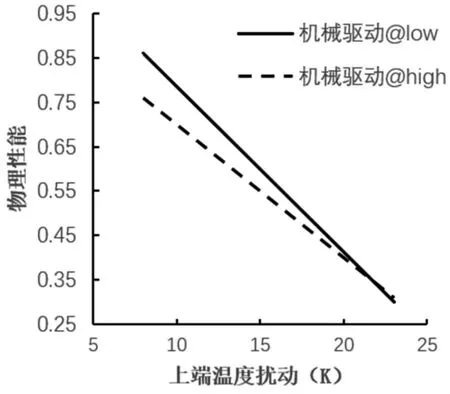
图5 上端温度与机械驱动影响的交互效应图
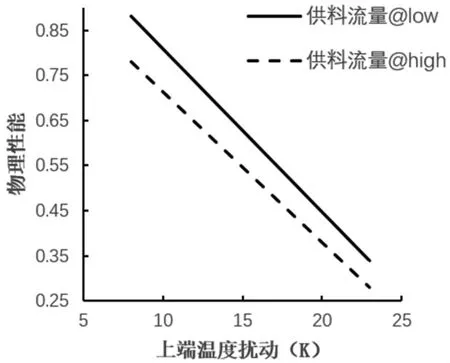
图6 上端温度与供料流量影响的交互效应图
4 驱动条件的优化结果
表2为两种侧壁温度分布下的驱动条件优化结果。其中,以线性分布的物理性能初始值为无量纲的基准值。从优化结果来看,两种温度分布优化后的物理性能较初始值都有一定的提升,并且线性分布的物理性能更优。同时,等温分布所需的上、下两端热驱动温差较线性分布要大。
5 结论
三种环流驱动中,热驱动的影响占主导作用。并且驱动条件对物理性能影响存在一定的交互性。
(2)通过DOE与梯度优化算法联用,物理性能较初始值有一定的提升。两种侧壁温度分布形式中,线性分布物理性能更优,所需的热驱动温差更低。
