北斗三号多频点双频组合共视时间传递性能分析∗

郭 栋 董绍武 武文俊王威雄张 健

(1中国科学院国家授时中心西安710600)(2中国科学院时间频率基准重点实验室西安710600)(3中国科学院大学天文与空间科学学院北京100049)

1 引言

GNSS(Global Navigation Satellite System)时间传递已成为当前远距离高精度时间比对的主要技术之一[1],主要包括GNSS共视(Common View,CV)、全视(All-in-View,AV)和精密单点定位(Precise Point Positioning,PPP)3种手段.早在20世纪80年代,GPS共视法就被国际权度局(BIPM)用于国际标准时间(Coordinated Universal Time,UTC)的计算[2–4].为了提高国际标准时间计算的准确度、稳定度和可靠性,2009年国际时频咨询委员会(Consultative Committee for Time and Frequency,CCTF)鼓励使用多种时间比对技术.不久,BIPM就将GLONASS(GLObal NAvigation Satellite System)卫星的共视比对结果加入到UTC的计算中.

目前,北斗(BeiDou)系统的建设已进入最后的收官阶段.截止2020年3月底,北斗三号(BeiDou-3)系统已发射3颗倾斜地球同步轨道卫星(Inclined Geosynchronous Satellite Orbit,IGSO)、24颗中圆地球轨道卫星(Medium Earth Orbit,MEO)和2颗地球静止轨道卫星(Geostationary Earth Orbit,GEO),不久将会发射最后一颗GEO卫星,届时BeiDou系统将全面建成,向全球用户提供更高精度的导航、定位和授时(PNT)服务.为了增强北斗系统与其他卫星导航系统的兼容与互操作性能,BeiDou-3系统在保留原来北斗二号(BeiDou-2)系统B1I和B3I信号的基础上还新增了B1C、B2a和B2b 3种新频率,与GPS和Galileo的信号频率均有重叠[5–6],具体见表1.

表1 GNSS信号频率分配情况Table 1 GNSS signal frequency distribution

2015年在国际时频咨询委员会制定的最新版时间传递标准(Common GNSS Generic Time Transfer Standard Version2E,CGGTTS-V2E)中除GPS、GLONASS外还包括Galileo、 BDS(BeiDou Navigation Satellite System)、 QZSS(Quasi-Zenith Satellite System)[7].随着北斗卫星导航系统的快速发展,其时间传递性能倍受国内外研究学者的关注,但很多研究主要是针对BeiDou-2系统,对BeiDou-3系统的时间传递性能分析较少.文献[8]认为,由于BeiDou-2系统主要覆盖亚太区域,在欧洲地区可视卫星数较少,故其亚欧共视时间比对链路的精度低于GPS和Galileo.文献[9]表明,在欧洲地区,BeiDou-2中MEO卫星的时间传递噪声要比GPS大,这可能是由伪距观测值中与卫星高度角相关的时延造成的,而且当两测站使用的接收机类型不同时,BeiDou-2系统中不同MEO卫星的共视结果存在偏差;在亚太区域,虽然BeiDou-2卫星可视数目较多,但GEO卫星和IGSO卫星的共视比对结果中存在比较明显的噪声.因此,期待BeiDou-3系统全面建成后能够在时间传递性能方面有所改善.本文通过建立中科院国家授时中心(NTSC)与捷克光电研究院(TP)之间的共视时间比对链路,对BeiDou-2系统B1I&B2I、B1I&B3I和BeiDou-3系统B1I&B3I、BIC&B2a双频无电离层组合链路的共视时间传递性能进行详细分析,并与GPS P1&P2、Galileo E1&E5a组合链路的共视比对结果进行比较来评估BeiDou-3系统的时间传递性能.

2 数学模型

2.1 BeiDou共视的基本原理

假设某一时刻,分别在保持有地方时间基准UTC(k)(k代表实验室)的A、B两地用高精度的时频接收机可同时观测到一颗或多颗BeiDou卫星,如图1所示.则可通过建立伪距观测方程解出两实验室本地参考钟分别与BDT的时差,再将两差值相减就可得到两守时实验室的钟差,计算过程如下:

式中,下角标i代表两实验室接收机共视到的第i颗BeiDou卫星,TA,i、TB,i分别为某一时刻A、B实验室与第i颗卫星间的星地钟差值;UTC(A)、UTC(B)分别为UTC在A、B两地的物理实现.n为同一时刻两地共视到的卫星总数,ωi表示用第i颗卫星计算的共视结果所占的权重,通常是依据卫星高度角定权以提高共视比对结果的精度.

图1 BeiDou共视的基本原理Fig.1 The basic principle of BeiDou common view

2.2 BeiDou双频消电离层伪距组合观测模型

在利用BeiDou卫星的伪距观测值解算星地钟差时会受到电离层、对流层和多路径误差以及卫星钟差和接收机钟差等误差的影响,伪距观测方程如下:

式中,为BeiDou卫星扣除接收机系统时延后的伪距观测值,ρs为站星间几何距离,c为真空中的光速,∆tr为接收机钟差,(∆tsv)f为顾及星上设备时延(Time Group Delay,TGD)的卫星钟差,其中TGD值与卫星信号频率f有关,S为由地球自转引起的Sagnac效应,dtrop为对流层误差,A为信号传播路径上的电子含量,为电离层误差,ϵ为包含多路径误差的伪距观测噪声.其中,dtrop造成的时延采用北大西洋公约组织(North Atlantic Treaty Organization,NATO)的流体静力学模型进行改正

其中,∆ttropo为对流层误差时延,f(E)是与高度角E有关的函数,表达式为

∆R(h)为高度h处天顶方向的对流层时延,定义如下:

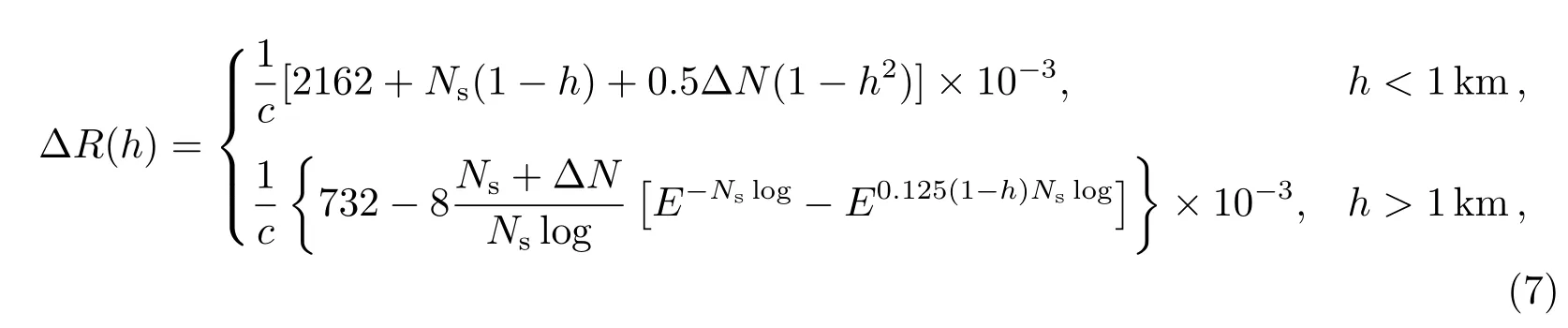
上式中

此处Ns=32.8,为平均海平面的折射率.以IGS(International GNSS Service)网站公布的各测站对流层天顶延迟(zenith path delay,ZPD)为参考,并与NATO模型计算的ZPD值进行比对,相同测站ZPD差值的RMS(Root Mean Square)约4–5 cm.为了有效削弱电离层误差对星地钟差解算结果的影响,通常采用双频无电离层伪距线性组合的方式,后面将给出详细介绍,其他误差模型可参考文献[7].

考虑到卫星的星上设备时延误差与卫星频率有关,因此在对BeiDou卫星的双频伪距观测值线性组合时TGD值也应做相应的组合变换.利用BeiDou卫星广播星历公布的钟差参数计算的卫星钟差中已经包含了BeiDou卫星B3I频率信号的星上设备时延,并将B3I信号的时延定为基准设备时延,其他频率信号的时延可通过导航星历文件中播发的与基准设备时延的差值间接求得[10–12].BeiDou其他频率信号经TGD改正后的卫星钟差如下:

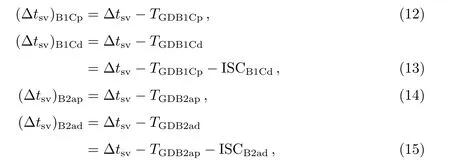
其中,TGD1、TGD2分别为B1I、B2I信号时延与基准设备时延的差值,该参数值在BeiDou广播星历文件中给出;B1Cp和B1Cd分别为B1C信号的导频分量和数据分量,TGDB1Cp为B1C数据分量的时延差,ISCB1Cd为B1C数据分量相对导频分量的时延修正项,TGDB1Cp和ISCB1Cd在B-CNAV1电文中播发;B2ap和B2ad分别为B2a信号的导频分量和数据分量,TGDB2ap为B2a数据分量的时延差,ISCB2ad为B2a数据分量相对导频分量的时延修正项,TGDB2ap和ISCB2ad在B-CNAV2电文中播发;∆tsv为根据BeiDou导航星历中给出的钟差参数计算的任意时刻t相对参考时刻toc的卫星钟差,计算过程如下:

其中,a0、a1、a2分别为参考时刻toc时的卫星钟差、卫星钟的钟速及其加速度的一半;∆tr为由卫星非圆形轨道而引起的相对论修正项,表达式为

上式中

此处,µ为引力常数,e、a、EK分别为BeiDou卫星轨道的偏心率、长半轴、偏近点角,3者均可从BeiDou卫星星历参数中得到.

假若利用BeiDou卫星的B1I和B2I伪距观测值进行双频无电离层组合,则组合后的TGD值为:

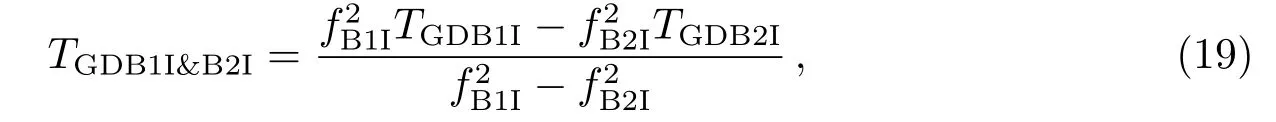
式中,fB1I、fB2I分别为北斗B1I和B2I信号的频率,TGDB1I、TGDB2I分别为北斗卫星B1I和B2I频率信号相对其B3I频率信号的星上设备时延差.

综上所述,由(4)–(18)式可推导出BeiDou任意双频消电离层组合观测模型,即:

式中,、分别为扣除系统时延后频率f1、f2的伪距观测值,ρ为站星几何距离,TGDf1、TGDf2分别为频率f1、f2的星上设备时延差,ζ为双频组合观测信号的噪声.

3 BeiDou-3共视时间传递性能分析

为了评估BeiDou-3系统的共视时间传递性能,建立了中科院国家授时中心(NTSC)与捷克光电研究院(TP)间的长基线GNSS共视时间比对链路.表2已给出本次试验所使用的接收机的配置信息,其中TP01和TP02接收机的GPS P1、P2信号时延已经过BIPM校准,正式用于国际标准时间(UTC)的计算.

表2 接收机配置信息Table 2 Receiver con figuration information

选用TP01和TP02两台多模多频接收机在2020年1月16日至2020年2月15日(简化儒略日MJD:58864—58893)的RINEX(Receiver Independent Exchange)格式观测文件,通过计算零基线共钟比对(common clock di ff erence,CCD)结果来评估BeiDou卫星不同双频无电离层组合信号的噪声水平.BeiDou组合频率的选取主要是依据文献[13]中对BeiDou-3双频组合的选取建议,同时考虑到两信号频率值相差越大,双频无电离层组合后伪距噪声的放大倍数越小.

利用开发的CGGTTS软件分别对GPS和BeiDou不同双频伪距组合观测信号处理生成标准的共视文件,Galileo采用接收机内置软件生成的标准共视文件.图2已分别给出GPS、Galileo及BDS-2、BDS-3不同频率组合的零基线共钟比对结果,其标准差(Std)的统计结果见表3.由图2和表3可明显看出,BeiDou-3卫星B1I&B3I、BIC&B2a组合要比BeiDou-2卫星B1I&B2I、B1I&B3I组合结果的噪声小;其中,BeiDou-2卫星的B1I&B2I组合的结果要比B1I&B3I组合噪声小,BeiDou-3卫星的BIC&B2a组合的结果要比B1I&B3I组合噪声小.BeiDou-3卫星BIC&B2a组合与Galileo卫星E1&E5a组合结果的噪声水平相当,且优于GPS卫星P1&P2组合.上述现象可能与各系统卫星的空间信号质量、组合频率信号的调制方式以及双频线性组合后伪距测量噪声的放大倍数有关[14–15].

图3、图4分别给出利用TP02接收机在同一时刻所能观测到的卫星数目及卫星高度角情况.由于BeiDou-2系统覆盖范围有限,故在TP同一时刻能观测的BeiDou-2卫星数目较少,且卫星高度角较低;同一时刻能观测到BeiDou-3和Galileo卫星的数目相近,主要集中在4–7颗,GPS卫星的观测数目相对较多,主要集中在5–8颗,最多同时能观测到12颗卫星.除BeiDou-2系统外,BeiDou-3系统、GPS和Galileo的卫星高度角分布情况比较接近.

表3 TP01与TP02接收机零基线共钟比对结果的标准差统计Table 3 The standard deviation statistics of the CCD results of TP01 and TP02 receivers

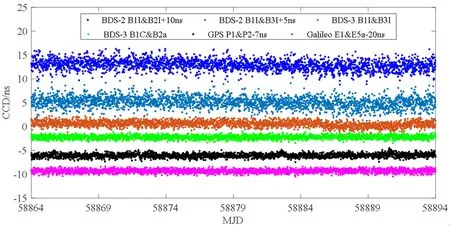
图2 TP01与TP02接收机零基线共钟比对结果Fig.2 The CCD results of TP01 and TP02 receivers

图3 TP02接收机在某一时刻观测到的卫星数情况Fig.3 The number of satellites observed by TP02 receiver at a certain time

图4 TP02接收机观测到的卫星高度角情况Fig.4 Satellite elevation observed by TP02 receiver

图5给出了同一时间段内(MJD:58864—58893)利用NT03和TP02接收机的RINEX格式观测数据计算的GPS、Galileo及BDS-2、BDS-3不同频率组合的共视时间比对结果,黑线是分别对各链路Vondark滤波降噪处理后的结果,滤波残差的RMS值已统计于表4.由图5和表4可明显看出,对BeiDou系统而言,BeiDou-3卫星B1C&B2a组合的共视比对链路的噪声最小,RMS值为0.8 ns,相比BeiDou-2卫星B1I&B2I、B1I&B3I组合和BeiDou-3卫星B1I&B3I组合共视时间比对结果的RMS值分别提高约46%、52%和37%.BeiDou-3 B1C&B2a组合的共视时间比对结果的RMS值与GPS P1&P2组合相当,且与Galileo E1&E5a组合相差仅0.04 ns.图6和表5分别给出了NTSC与TP间6条共视时间比对链路的稳定性和对应的修正阿伦偏差(Modi fied Allan Deviation)值,Tau为采样间隔.可明显看出,BeiDou-3卫星B1C&B2a组合的共视时间比对链路的短期(<1 d)稳定性要优于BeiDou-2卫星的B1I&B2I、B1I&B3I组合和BeiDou-3卫星的B1I&B3I组合,且与GPS P1&P2组合和Galileo E1&E5a组合的共视比对链路稳定性相当,6条链路的中长期(>1 d)稳定性基本一致.

表4 NTSC与TP间不同链路共视比对结果的滤波残差统计Table 4 Statistics of filtering residuals of the di ff erent links results of common view time comparison between NTSC and TP

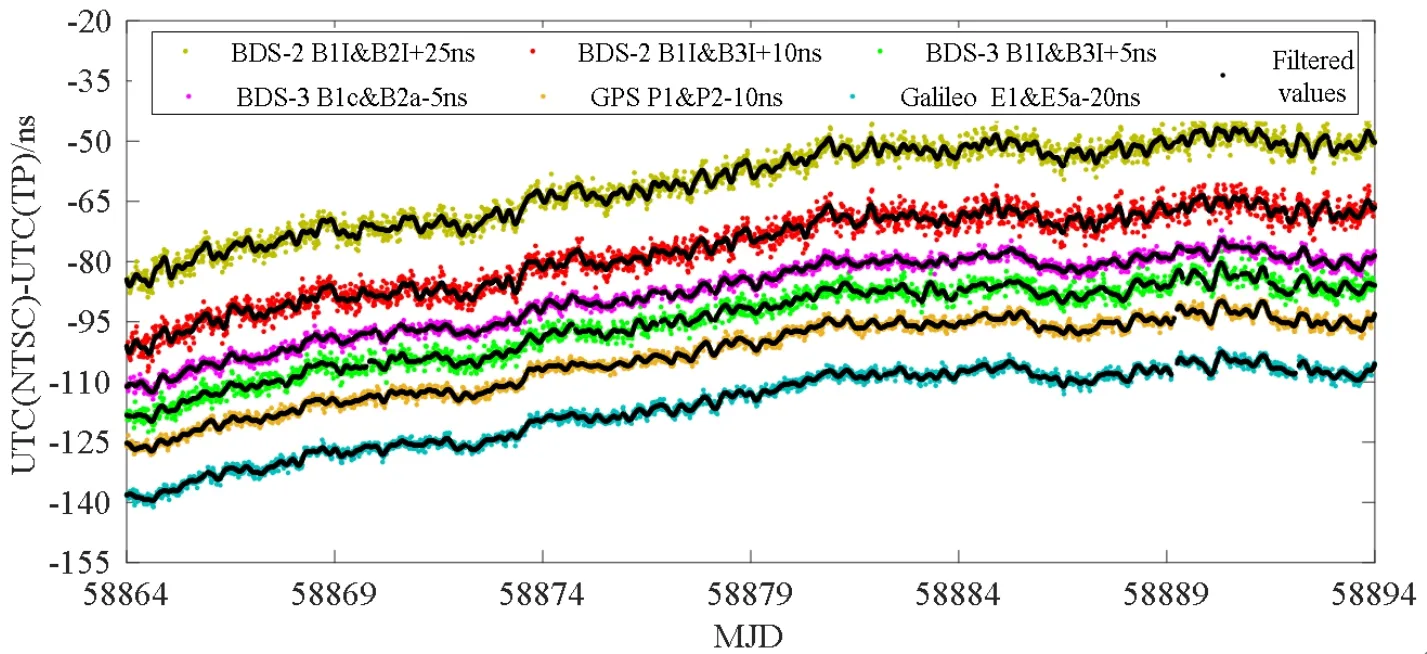
图5 NTSC与TP间共视时间比对结果Fig.5 The results of common view time comparison between NTSC and TP

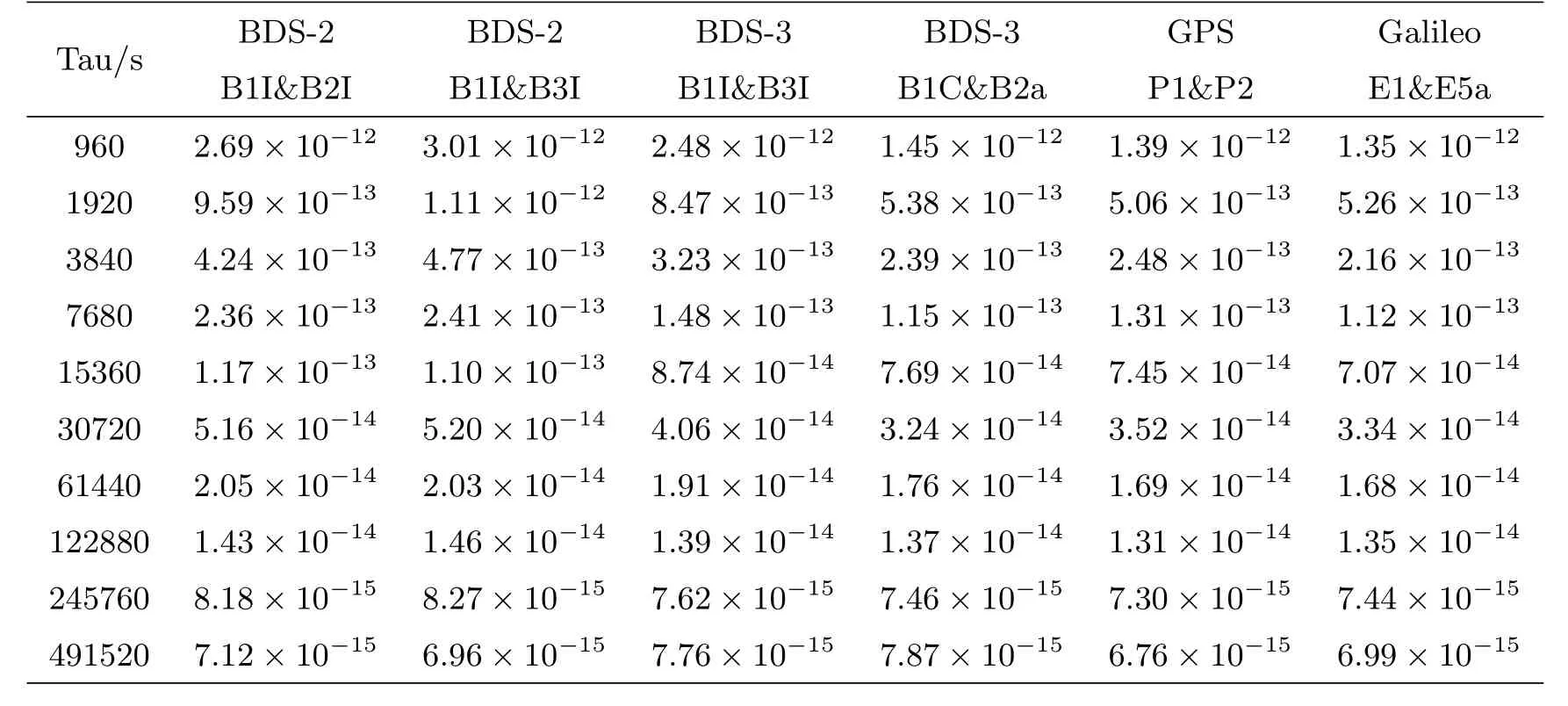
表5NTSC与TP间不同链路的修正阿伦偏差值统计Table 5 The statistics of modi fied Allen deviation values of di ff erent links between NTSC_and_TP

图6 NTSC与TP间共视时间比对链路的稳定性Fig.6 The stability of common view time comparison links between NTSC and TP

图7和图8已分别给出在不同时刻NTSC和TP间各卫星导航系统能共视到的卫星数目及其在同一时刻各导航系统共视卫星数所占的比例情况.由图7–8可看出,现阶段同一时刻在NTSC和TP能共视到BeiDou-3卫星的数目相比其他系统较少,通常为1–2颗.

图7 不同时刻NTSC与TP间共视卫星数Fig.7 The number of common view satellites between NTSC and TP at di ff erent times

图8 同一时刻NTSC与TP间共视卫星数统计Fig.8 Statistics of the number of common view satellites between NTSC and TP at the same time

4 结论

本文依据CCTF制定的GNSS共视时间传递标准CGGTTS-V2E,利用自主开发的CGGTTS软件分别对GPS和BeiDou卫星不同频率的双频伪距组合信号进行处理,生成标准格式的共视文件.通过建立NTSC与TP间GPS、Galileo和BeiDou系统的共6条长基线共视时间比对链路,初步评估了BeiDou-3系统的共视时间传递性能,并与GPS、Galileo的共视时间比对结果进行了比较,现得到如下结论:

(1)对BeiDou系统而言,在BeiDou-3共视卫星数相对较少的情况下,其B1C&B2a组合共视时间比对链路所受噪声的影响相比BeiDou其他双频组合有明显的改善,经Vondark滤波降噪后,其滤波残差的RMS值相比BeiDou-2 B1I&B2I、B1I&B3I和BeiDou-3 B1I&B3I组合分别提高约46%、52%和37%;与GPS P1&P2组合相当,且与Galileo E1&E5a组合相差不大;

(2)共视时间比对链路的短稳(<1 d)方面,BeiDou-3 B1C&B2a组合要优于BeiDou-3 B1I&B3I和BeiDou-2 B1I&B2I、B1I&B3I组合链路,且与GPS P1&P2和Galileo E1&E5a组合链路的短稳相当,6条链路的中长稳(>1 d)基本一致.

未来,BeiDou-3系统的B1C、B2a信号可作为GNSS共视时间传递标准中BeiDou系统的补充频点,进一步增强国际时间比对链路的可靠性.随着BeiDou-3系统可用卫星数的增多,其时间传递性能还有提升的空间,希望BeiDou系统能够早日用于UTC的计算.