3颗脉冲星自转性质的研究∗

胡 悦李 琳党世军王兆军 袁建平王榆斌

(1新疆大学物理科学与技术学院乌鲁木齐830046)(2中国科学院新疆天文台乌鲁木齐830011)(3中国科学院大学北京100049)

1 引言

脉冲星是死亡恒星经过超新星爆发的产物之一,通常被认为是高速自转的强磁场中子星.大多数的中子星通过将转动能转化为辐射能的方式向宇宙发射出脉冲信号,朝向地球辐射的脉冲信号被射电望远镜接收时即在观测上表现为脉冲星.

脉冲星计时是一种对脉冲到达时间进行分析研究的方法,通过观测和分析脉冲到达时间获得脉冲星的自转周期、自转周期导数和色散等基本参数,进而推算其特征年龄、自转能损率、表面磁场等信息,几年的观测能使我们测定出脉冲星位置、自行等参数.在获得一系列的参数后,我们可以建立到达时间模型[1].在长期对脉冲星到达时间的观测中,发现部分脉冲星是不稳定的,表现为可能由自转不稳定产生的计时噪声和内部物理变化导致的周期跃变事件.

计时噪声主要在到达时间残差(实测的脉冲到达时间与自转模型预测的脉冲到达时间之间的差值)上表现为没有规律的随机起伏.文献[2]首次认识到了计时噪声的存在,认为蟹状星云脉冲星中的计时噪声是相位、自转频率(ν)或者是自转频率1阶导数(˙ν)的随机行走导致的.文献[3]通过对300多颗脉冲星到达时间数据的分析研究,认为计时噪声与自转频率1阶导数有关,并且发现随着时间跨度的增长,计时噪声结构出现准周期的概率会变大.关于计时噪声的成因依然是一个谜,有研究者认为可能是脉冲星自身的原因产生的,文献[4]认为中子星壳层和内核超流的耦合变化是产生计时噪声的原因,还有研究者认为可能是外部的原因造成的,如外部磁层的波动[5–7].周期跃变是一种脉冲星自转突然加快的现象,通常在周期跃变发生后脉冲星的自转周期伴随着一个恢复过程,自转周期一般不会恢复到与发生周期跃变之前相同的状态.一般认为周期跃变现象是中子星内部的物理变化导致的.

文献[7]报告了计时残差显示出准周期性的17颗脉冲星,它们的自转频率1阶导数随时间的变化也有准周期性,其中6颗脉冲星的自转频率1阶导数的变化与脉冲轮廓宽度的变化有很强的相关性,这说明了它们的计时噪声与脉冲星辐射有关联.文献[8]的研究发现PSR J1602−5100脉冲轮廓的变化与自转频率1阶导数的变化有很强的相关性.文献[9]研究了PSR J0742−2822脉冲轮廓与自转频率1阶导数之间的关联,发现在周期跃变事件发生后,脉冲轮廓与自转频率1阶导数的相关性明显增强.更特殊的源是间歇脉冲星,文献[10]通过对间歇脉冲星PSR B1931+24的长期计时观测发现它在有辐射的“on态”和没有辐射的“o ff态”对应着不同的自转频率1阶导数,在“on态”的自转频率1阶导数明显大于“o ff态”,这一工作无疑证明了脉冲星自转频率1阶导数与脉冲辐射存在相关性,目前的理论认为观测的脉冲辐射来源于脉冲星的磁层,进而证明自转频率1阶导数随时间的演化与磁层的变化息息相关.

我们使用PSRCAT1https://www.atnf.csiro.au/research/pulsar/psrcat.脉冲星表选出了3颗脉冲星,分别为PSR J1539−5626、J1832−0827和J1847−0402,它们的自转参数与文献[7]中的6颗自转变化与辐射变化具有相关性的脉冲星接近.我们对它们的自转频率、自转频率1阶导数与脉冲轮廓的变化作了分析研究,研究了它们的自转变化与辐射变化是否具有相关性.

2 观测及数据处理

本文的观测数据均来源于新疆天文台南山25 m射电望远镜与澳大利亚Parkes 64 m射电望远镜,其中Parkes数据从澳大利亚科学与工业研究组织数据库2https://data.csiro.au/dap/public/atnf/pulsarSearch.zul.下载.3颗脉冲星数据的基本信息见表1.

表1 3颗脉冲星的观测基本信息.从左至右每一列分别代表脉冲星的名称、观测的儒略日期、数据的数目、观测的中心频率、望远镜和数据积分时间Table 1 The information of observations on three pulsars.Each column from left to right represents the pulsar name,observation date,number of data,center frequency,telescope,and integration time

南山25 m射电望远镜从2002年7月开始使用制冷接收机,接收机工作频率为1380–1700 MHz,带宽共320 MHz,中心观测频率为1540 MHz.在2010年1月前,数据记录在模拟滤波器组,通道为2(双极化)×128(子通道)×2.5 MHz(每个子通道的频率).从2010年1月起,数据被记录在数字滤波器组,通道为2×1024×0.5 MHz.Parkes 64 m射电望远镜的观测数据中除了小部分数据记录于模拟滤波器组,大部分数据被记录在数字滤波器组[11].PSR J1539−5626的计时数据跨度为10 yr,PSR J1832−0827和J1847−0402的数据跨度都为20 yr.

脉冲星的自转可以用如下模型来描述:

其中t0是参考时间,Φ(t)是自转相位,Φ0是参考相位,ν、˙ν和¨ν分别是脉冲星的自转频率,自转频率1阶导数和自转频率2阶导数.为了从观测数据获得脉冲星自转参数,我们使用PSRCHIVE[12](PSRCHIVE是一个开源的C++库,通常被用于脉冲星计时处理、闪烁分析、偏振校准、单脉冲处理和消干扰等)对观测数据进行了处理,步骤如下:(1)使用paz和pazi命令消除射频干扰,并且使用pam命令在频域,时域和偏振上进行折叠以得到每个观测数据的平均脉冲轮廓;(2)选取一个标准轮廓(由所有的观测数据相位对齐叠加而得到,临时的标准轮廓可选用一个信噪比高的观测轮廓),使用pat命令得到每个观测数据的脉冲到达时间;(3)为消除地球自转和公转的影响,将脉冲到达时间归算到太阳系质心(SSB).使用Tempo2[13–14]软件包用最小二乘法拟合(1)式,获得残差为白噪声的模型,其初始模型参数来源于ATNF3https://www.atnf.csiro.au/research/pulsar/psrcat/expert.html.(Australia Telescope National Facility);(4)使用pam命令将白噪声模型写入每一个数据,并且将观测数据使用psradd命令叠加获得高信噪比的标准轮廓;(5)重复上述(1)–(3)步以获得最佳的参数表,其中需要消除不同终端和不同观测频率的系统差.上述过程均使用太阳系星历表[15](DE421)和质心坐标时间(TCB).

脉冲星的位置、自行、噪声、自转参数,它们都相互影响.为了无偏差地得到脉冲星的自转参数,需要精确估算脉冲星的位置、自行和计时噪声功率谱.文献[16]提出了乔勒斯基(Cholesky)方法,首先得到计时残差的协方差矩阵,随后对矩阵进行乔勒斯基转换,进而白化残差和时间模型._具体步骤如下:首先估计残差红噪声成分的功率谱模

型,其表达式是

其中P是功率谱,f是频率,A是振幅,fc是转角频率,α是谱指数.fc设定为低频红噪声功率谱发生偏转所对应的频率,如果谱指数分别是−2、−4、−6,那么它们分别代表脉冲相位噪声、自转频率噪声和自转减慢噪声.然后基于此频谱,用全局最小二乘拟合方法拟合脉冲星的参数(包含脉冲星的位置、自行和自转参数).接下来,基于得到的新参数,重复上述操作以得到改进后的红噪声频谱新模型,从而获得最佳的脉冲星参数.整个过程迭代持续到结果收敛为止.这些步骤通过TEMPO2软件包的插件spectralModel来完成.当计时残差呈现强的低频噪声时,此方法能提高脉冲星参数精度,同时也适用于非均匀间隔观测以及误差变化的观测,文献[17]使用此方法分析了毫秒脉冲星的计时噪声功率谱,文献[18]应用此方法研究了普通脉冲星的自行.表2展示了应用此方法获得的3颗脉冲星的位置和自转参数.在更新了3颗脉冲星的位置之后,我们为了获得精确的自行结果,使用位置比较法(比较两次不同历元的位置)计算得出脉冲星的自行,其中3颗脉冲星以前的位置使用了尽可能早的观测数据.PSR J1539−5626的位置参数来自文献[19],J1832−0827和J1847−0402的位置参数来自文献[20].计算结果展示于表2,我们测得J1539−5626自行的误差比文献[21]大24%,对于J1832−0827的自行,本工作的误差与文献[20]相当,J1847−0402的误差为文献[18]误差的40%.

表2 3颗脉冲星到达时间模型基本参数表.从左往右每一列分别代表脉冲星的名称、赤经、赤纬、获得参数的日期、自转频率、自转频率1阶导数、赤经及赤纬方向的自行Table 2 Basic parameters of three pulsars.From left to right,each column represents the pulsar name,right ascension,declination,the derived date of the parameters,rotation frequency, first derivative of rotation frequency,proper motion in right ascension and declination

3 结果

3.1 自转参数的演化

首先我们分别得到了PSR J1539−5626、J1832−0827和J1847−0402这3颗脉冲星的到达时间残差,分别展示在图1、图2和图3中的图(a),其中PSR J1832−0827和J1847−0402均使用了南山和Parkes的到达时间数据,这是为了研究脉冲星的自转参数变化,获得更加精确的计时结果.这3颗脉冲星均拟合了自转频率、自转频率1阶导数和自转频率2阶导数(¨ν),它们残差的加权均方根误差分别为12.6 ms、4.3 ms和5.8 ms.长时标的计时观测表明,3颗脉冲星的计时残差均被红噪声主导.

由于计时噪声的随机性和望远镜观测日期的不确定性,我们在研究自转频率及其1阶导数的演化时根据数据疏密程度取不同的时间区间,分别拟合这些区间内的计时数据,使得拟合后的计时残差为白噪声,得到其自转频率和频率1阶导数.PSR J1539−5626观测跨度相对较短,在MJD 56750之前,将每段区间的时标设为200 d,单独拟合自转频率与其1阶导数,重复100 d(其中重复的天数代表相邻两个参数之间存在时间重叠),在MJD 56750之后,将每段区间的时标设为400 d,重复200 d.PSR J1832−0827和J1847−0402观测跨度较长,我们将其均分为36段,每段区间的时标为400 d,重复200 d.

图1 图(a)是PSR J1539−5626的到达时间残差变化,图(b)、(c)分别是PSR J1539−5626自转频率及其1阶导数的变化,图(d)为PSR J1539−5626的半高全宽(FWHM).图(a)中Wrms代表加权均方根误差.Fig.1 Panel(a)is the post- fit residuals of PSR J1539−5626,panels(b)and(c)are respectively the change of frequency and its first derivatives of PSR J1539−5626,and panel(d)is the FWHM(full width at half maximum)of PSR J1539−5626.Wrms in the panel(a)represents the weighted root mean square error.

3颗脉冲星自转频率及其1阶导数的演化结果分别展示于图1、图2和图3中的图(b)和(c),其中图(b)显示的是自转频率减去其线性变化趋势后的频率残差∆ν,图(c)是自转频率1阶导数减去平均值后的残差.可以看出,在10–20 yr的时标中,3颗脉冲星的自转频率残差∆ν随时间的变化幅度最大的是PSR J1539−5626,∆ν∼12.6(3)×10−9Hz,最小的是PSR J1832−0827,∆ν∼2.2(4)×10−9Hz.

PSR J1539−5626的自转频率残差在MJD 54700–56750间呈线性变化,自转频率残差从0.521(5)×10−8Hz变化到−0.586(2)×10−8Hz.在整个观测时间段内,PSR J1539−5626自转频率1阶导数的变化幅度大约为0.61(3)×10−15s−2,相对变化大小是

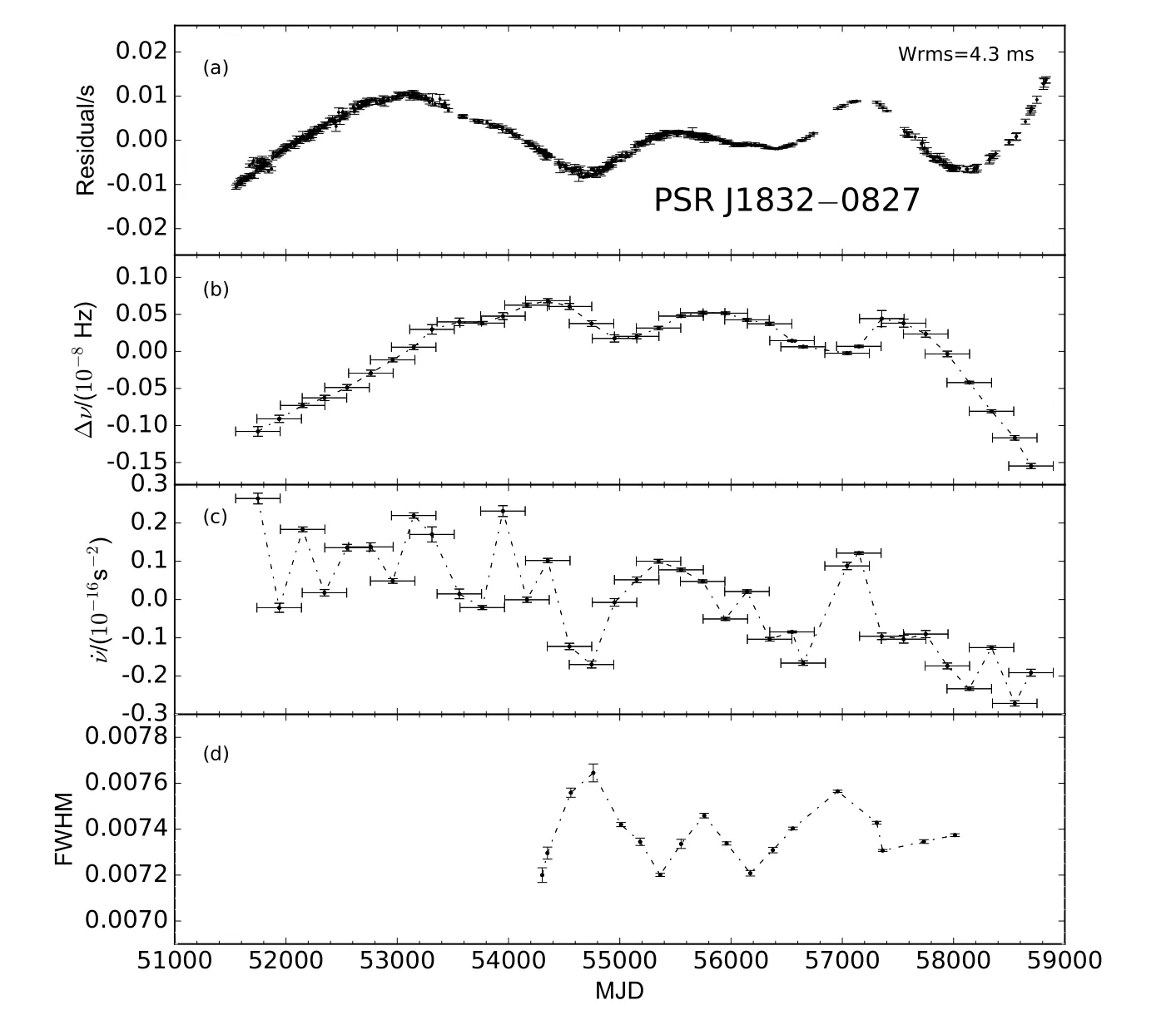
图2 同图1,PSR J1832−0827的到达时间残差、自转频率、自转频率1阶导数及FWHM.Fig.2 Same as Fig.1,the post- fit residuals,spin frequency and its first derivatives,and the FWHM of PSR J1832−0827.

PSR J1832−0827的自转频率残差在MJD 51700–54300区间(区间1)上升了1.65(2)×10−9Hz,在MJD 57000–59000(区间2)下降了1.98(13)×10−9Hz,自转频率1阶导数在区间1内有明显的振荡,振荡幅度约为0.29(6)×10−16s−2,自转频率1阶导数在区间2内的振荡范围约为0.12(2)×10−16s−2到−0.27(3)×10−16s−2之间,区间1的自转频率变化率小于区间2.在20 yr时标上自转频率1阶导数的变化为0.54(5)×10−16s−2,相对变化大小为|∆˙ν|/|˙ν|≃0.35(9)×10−3.PSR J1832−0827的自转频率1阶导数在整体上有下降的趋势,我们线性拟合得到¨ν=−5.29(4)×10−26s−3.

PSR J1847−0402自转频率残差变化幅度约为4.2(7)×10−9Hz,比PSR J1832−0827自转频率残差变化范围大.PSR J1847−0402在MJD 51500–56500之间自转频率1阶导数呈小幅度振荡,在MJD 56500–57750之间,自转频率1阶导数振荡幅度较大,∆˙ν≃1.1(2)×10−16s−2,在MJD 57750之后又恢复小幅度振荡.在20 yr时标上,PSR J1847−0402自转频率1阶导数的变化幅度为0.11(2)×10−15s−2,相对变化幅度为|∆˙ν|/|˙ν|≃0.76(2)×10−3,其自转频率1阶导数整体上有上升趋势,我们线性拟合得到¨ν=7.69(8)×10−26s−3.

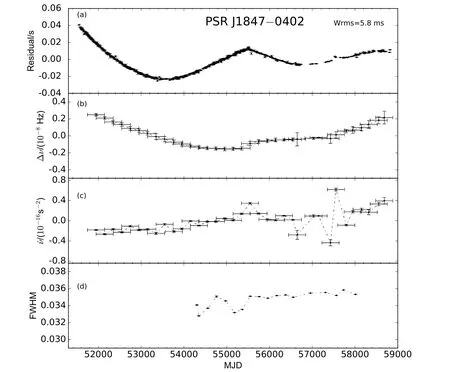
图3 同图1,PSR J1847−0402的到达时间残差、自转频率、自转频率1阶导数及FWHM.Fig.3 Same as Fig.1,the post- fit residuals,spin frequency and its first derivatives,and the FWHM of PSR J1847−0402.

3.2 计时噪声

由于PSR J1832−0827与J1847−0402的自转频率1阶导数˙ν整体上呈线性变化的趋势,我们求出了其斜率,也就是自转频率的2阶导数¨ν.脉冲星自转的制动指数表示为:

我们计算并分别得到了PSR J1832−0827与J1847−0402的制动指数,分别为−3.51(2)和6.15(5).由于PSR J1539−5626没有稳定的¨ν,所以我们没有计算它的制动指数.磁偶极制动模型下,如果没有其他制动,其制动指数n=3.从理论上讲,如果还认同脉冲星磁偶极制动的大框架,制动指数就不可能为负,因此PSR J1832−0827的制动指数没意义.从观测上来讲,文献[3]给出来几百颗脉冲星的自转频率2阶导数¨ν,这个数值会随着观测时间长短的不同发生变化.只有几颗年轻脉冲星的¨ν在短时标和长时标的测量都是稳定的,能反映出其中的物理信息.

脉冲星的计时残差可以用来研究计时噪声的功率谱.乔勒斯基方法使用预白化方法来消除红噪声频谱泄露,在分析脉冲星计时噪声功率谱过程中调用了红噪声的协方差矩阵.我们在图4画出了所得到的计时噪声功率谱,它们的低频红噪声与幂律谱符合较好.可以看出PSR J1539−5626和J1832−0827的低频噪声功率谱谱指数接近−6,表明它们的计时噪声可能是自转频率1阶导数噪声主导的.PSR J1847−0402的低频噪声功率谱谱指数大约为−4.5,它的计时噪声可能是自转频率噪声主导的.乔勒斯基方法的不足之处在于不能给出谱指数的误差.文献[22]中使用贝叶斯的方法得到PSR J1539−5626和J1832−0827的噪声功率谱,也同样符合幂律模型,其谱指数分别是,频谱较为缓和.PSR J1539−5626和J1832−0827低频噪声强度分别为1.77×10−17yr3和4.43×10−18yr3,PSR J1847−0402低频噪声强度是2.09×10−18yr3.

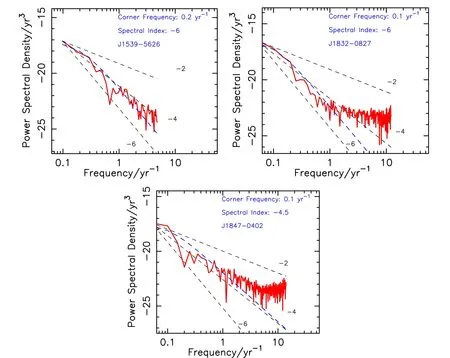
图4 PSR J1539−5626、J1832−0827和J1847−0402的噪声功率谱.其中红色线段代表红噪声,蓝色虚线代表我们拟合的结果,黑色的虚线从上至下分别代表谱指数为−2、−4、−6时的噪声功率谱,其中幂律谱拟合结果展示在每张子图的右上角,从上至下分别为转角频率,谱指数的值和脉冲星的名称.Fig.4The power spectra of timing noises in PSR J1539−5626,J1832−0827,and J1847−0402.The red line represents the red noise,the blue dashed line represents the result of our fitting,and the black dashed lines represent the power spectra of timing noises when the spectral index is respectively−2,−4,and−6 respectively from top to bottom.The result of fitting the power law spectrum is displayed in the upper right corner of each sub-graph,from top to bottom represents the value of corner frequency,the value of the spectral index,and the name of the pulsar,respectively.

3.3 脉冲轮廓变化

理论上认为脉冲星的辐射特性反映脉冲星辐射区的结构和辐射机制,脉冲宽度是辐射束结构的重要参数,通常使用FWHM来表征,定义为脉冲峰值强度一半位置处的宽度.本文研究Parkes望远镜在中心频率1369 MHz观测获得的脉冲平均轮廓的宽度.每次观测得到的平均脉冲轮廓都由几百个单脉冲数据叠加而成,持续观测的时标通常为2 min到4 min.3颗脉冲星脉冲轮廓的半高全宽随时间的变化分别展示于图1、图2和图3中的图(d),它们均显示出一定的变化.PSR J1539−5626脉冲的半高全宽在0.029–0.035相位之间振荡.PSR J1832−0827的脉冲更窄,其宽度在0.0072–0.0077相位之间变化.PSR J1847−0402的宽度与PSR J1539−5626接近,在0.032–0.036相位之间振荡.

为了检验脉冲轮廓的变化,我们将脉冲轮廓的半高全宽平均值设定为阈值,将其分为两类,然后分别叠加并获得3颗脉冲星的平均脉冲轮廓,见图5,脉冲轮廓已归一化且红色虚线代表脉冲峰值50%强度.可以看出,3颗脉冲星均展示出两个稳定的平均脉冲轮廓(分别为宽模式和窄模式).PSR J1539−5626脉冲轮廓有2个峰,脉冲在相位0.488–0.492及0.510–0.526两个区间明显变化.宽模式的右峰相对强度是58.7%,窄模式的右峰相对强度是53.6%.宽和窄两种模式的FWHM宽度分别是0.0304(1)和0.0332(6),宽度差值是0.0028(6).统计得到PSR J1539−5626有47%的时间处于宽模式.PSR J1832−0827的脉冲轮廓变化发生在相位0.5–0.505之间,变化幅度比较小.宽和窄两种模式的FWHM宽度分别是0.00715(3)和0.00774(1),宽度差值是0.00059(3).PSR J1847−0402的脉冲轮廓至少有3个峰(3个成分),从左至右分别是成分I、成分II和成分III.脉冲成分I在相位0.47–0.48之间,我们注意到较宽的脉冲轮廓(绿色)脉冲成分I峰值强度是0.545(3),位于红色虚线的上部.而较窄的脉冲轮廓(蓝色)脉冲成分I的峰值强度是0.493(5),处在红色虚线的下部.这就导致了较窄的脉冲轮廓在此区间(蓝色)未达到计算半高全宽的阈值条件.我们分别计算了两种模式的宽度,其中宽模式的脉冲宽度是0.03506(4),窄模式的脉冲宽度是0.03495(1).宽度差值是0.00011(4).PSR J1847−0402有55%的时间处于宽模式.3颗脉冲星宽窄两种模式的占有时间统计展示于表3.

表3 对3颗脉冲星两种不同平均脉冲轮廓持续时间的统计Table 3 Statistic of the duration for two di ff erent integrated pulse pro files of three pulsars

图5 3颗脉冲星的积分脉冲轮廓(归一化)的变化.其中绿色和蓝色的脉冲轮廓分别代表宽模式和窄模式,PSR J1832−0827由于两种模式宽度变化较小,故我们在图中将其放大以便能清晰看出两种模式的变化.Fig.5 The variations of integrated pulse pro files of three pulsars(normalized).The green and blue pulse pro files represent the wide mode and the narrow mode,respectively.PSR J1832−0827 has a small change in the width of the two modes,so we enlarge it in the figure so that we can clearly see the changes in the two modes.

4 讨论

本文所研究的PSR J1539−5626、J1832−0827和J1847−0402这3颗脉冲星相对年轻,它们的特征年龄处于1.61×105–7.95×105yr之间,表面磁场处于1.1×1012–6.51×1012Gs. 它们自转频率变化率在10−13s−2数量级,自转能损率在1034erg·s−1数量级,因此它们相对活跃,计时噪声比较明显.

我们分析了3颗脉冲星的自转参数随时间的变化,它们都表现出了自转频率、自转频率1阶导数的明显变化.自转频率的变化幅度为2.2(4)–12.6(3)nHz.自转频率1阶导数的变化相对大小介于0.035(9)%–0.75(5)%之间.其中PSR J1539−5626自转频率1阶导数的变化相对大小(0.75(5)%)与文献[7]中的J1717−3425、J1909+0007和J1830−1059的自转频率1阶导数的变化相对大小(分别是0.79%、0.75%、0.71%)接近.J1539−5626的年龄(0.795×106yr)和自转能损率(1.3×1034erg·s−1)与J1717−3425,J1909+0007和J1830−1059的年龄(0.107×106–2.92×106yr)和自转能损率(0.21×1034–3.6×1034erg·s−1)接近.而J1832−0827和J1847−0402自转频率1阶导数的变化相对大小比文献[7]自转频率1阶导数的变化相对大小的最小值的0.31%还小.

PSR J1539−5626在MJD 56700–57400自转频率残差相对于MJD 54700–56700区间有一个缓慢增加过程,这类似于慢跃变.目前已经在PSR B1822−09、B1642−03、B0919+06、J1602−5100、J0631+1036、B1907+10、J1539−5626和J1602−5100中探测到31次慢跃变.慢跃变的频率变化幅度是2.3–176 nHz,可以看出这3颗脉冲星的计时噪声的自转频率变化幅度在慢跃变频率变化幅度范围内.在观测特征上,慢跃变可以看作是计时噪声的特殊表现形式.那么,慢跃变与计时噪声在物理本质上是否有一致或者明显区别,这有待于进一步研究.

脉冲星计时噪声普遍存在于脉冲星中,计时噪声的强度与自转减慢率有很强的相关性[3,22–23].年轻脉冲星的计时噪声比年老的脉冲星(比如毫秒脉冲星)计时噪声更强,我们研究的3颗脉冲星的噪声强度介于2.09×10−18–17.7×10−18yr3之间,毫秒脉冲星的噪声强度范围为2.55×10−28–2.55×10−23yr3,因此这3颗脉冲星的噪声比毫秒脉冲星的噪声强5–10个数量级.长时标(如5 yr以上)的观测显示,脉冲计时残差通常表现为随机性或者准周期性的变化.

对于计时噪声在长时标观测中呈准周期变化的现象有不同的解释,文献[24]和文献[25]认为是轨道伴星的影响;文献[26]认为是脉冲星的自由进动所造成;文献[8]认为是脉冲轮廓的变化所导致,文献[27]认为是脉冲星在稳定磁层状态之间转换造成的.尽管如此,关于脉冲星计时噪声的起源问题依旧是一项难题,如果我们能够很好理解计时噪声,并且通过建立模型来消除计时噪声,这将有助于我们搜寻引力波以及研究脉冲星的起源与演化过程.

文献[28]分析了毫秒脉冲星射电辐射的长期稳定性,探测到了PSR J1643−1224、J1713+0747、B1937+21和J2145−0750脉冲轮廓的长时标变化.我们推测,脉冲轮廓变化可能是更普遍的现象,随着高灵敏的观测可能会探测到更多的此类现象.引起脉冲轮廓变化的原因有:脉冲星磁层的变化、测地线进动、无力矩进动、电离星际介质的传播效应(包括衍射闪烁和散射展宽)、偏振错误定标、无线电射频干扰等.脉冲星信号被银河系的电离星际介质散射,经过不同的路径抵达望远镜,可以引起脉冲轮廓的展宽.计算散射展宽的公式是

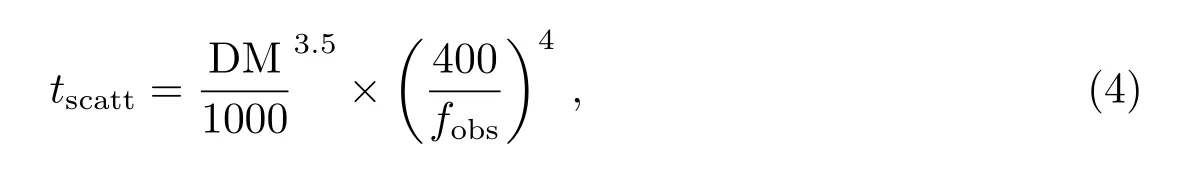
其中DM是脉冲星的色散量,fobs是观测接收机的中心频率(单位MHz).对于在中心频率为1369 MHz观测的J1539−5626、J1832−0827和J1847−0402这3颗脉冲星,计算得到它们脉冲轮廓的散射展宽分别是16.62(3)µs、10.89(2)µs和7.86(5)µs,散射展宽占脉冲周期的比例是0.068×10−3、0.017×10−3、0.013×10−3.可以看出,散射展宽明显小于观测到的轮廓变化值,所以散射展宽不是它们脉冲轮廓变化的原因.除了间歇脉冲星外,目前已经探测到10颗脉冲星的辐射长时标变化与自转具有相关性.文献[8]指出,虽然一些脉冲星自转减慢率变化与脉冲轮廓变化之间存在相关性,但是自转变化与轮廓变化之间的内在关联可能更复杂.为了探究这3颗脉冲星自转与辐射是否具有相关性,我们分别计算了这3颗脉冲星的自转频率1阶导数与脉冲轮廓半高全宽之间的相关系数,得到的相关系数呈现随机分布,没有探测到明显的相关性.

5 总结与展望

使用南山射电望远镜和Parkes射电望远镜的脉冲星计时数据,我们探测到了PSR J1539−5626、J1832−0827和J1847−0402这3颗脉冲星自转频率和自转频率1阶导数具有明显的变化.低频红噪声来自于自转减慢率和自转频率的变化,其功率谱符合幂律谱.本工作使用Parkes射电望远镜的观测数据研究了它们脉冲轮廓宽度,探测到了它们脉冲轮廓的变化,没有探测到自转变化与辐射变化的相关性.我们希望能申请到大射电望远镜比如贵州500 m球面射电望远镜(FAST)来继续我们的研究,也同时期寄未来新疆奇台110 m射电望远镜(QTT)的建成,这能帮助我们观测到更精确的脉冲到达时间并获得高信噪比的脉冲辐射,便于我们进一步研究脉冲星自转与辐射之间的相关性.我们也打算下一步通过单脉冲数据分析研究其模式变化现象,尝试结合理论模型来加深对脉冲星辐射机制的认识,这也有助于探索和检验计时噪声的起源.

致谢感谢寇菲菲阅读此文并提出修改意见.The Parkes radio telescope is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO.