基于光变曲线的空间碎片基本形状分类∗

鹿 瑶 赵长印

(1中国科学院紫金山天文台南京210023)(2中国科学院空间目标与碎片观测重点实验室南京210023)(3中国科学院大学北京100049)

1 引言

随着空间碎片观测网探测能力的增强,越来越多的未编目碎片被探测到,对于新发现的空间碎片,了解其基本形状、材料等信息是必要的,也是空间态势感知的重要组成部分.光学探测直接获得碎片的测角信息和光度信息,其中影响碎片光度的参数包括观测几何量以及目标尺寸、形状、表面材料光学特性、姿态等.碎片的旋转运动导致光度数据随时间变化,连续观测得到的光度变化曲线也叫光变曲线.不同类型的碎片会产生特征不同的光变曲线,这些特征可以反映碎片的基本形状和表面材料类型等,例如失控卫星的光变曲线往往含有一些镜反射特征,而常规火箭体的光变曲线常常表现为光滑的双峰结构等.因此可以通过研究光变曲线,获得未知碎片形状、材料等信息,对碎片基本类型进行分类.

基于光度信息,国内外学者研究了多种碎片类型分类方法.张逸平等[1–2]基于自主数据库,统计了一批空间目标的星等-相位角特征曲线,结果表明部分球状、圆柱状碎片的特征曲线与理论相符,但很难利用文中总结的4类特征进行碎片分类;王文竹等[3]基于空间目标光学散射截面等信息,利用机器学习方法对目标进行分类,实现了90%以上的识别率,但输入特征除了光学数据外还包括了雷达探测资料.上述方法虽然使用了光度信息,但输入特征并不是光变曲线.随着机器学习方法的不断发展,在天文学领域,无论是1维光变曲线的分类还是2维天文图像的特征识别,机器学习方法都有很多成功应用.以深度神经网络对光变曲线的分类为例,Pearson等[4]测试了多种机器学习方法从恒星光变曲线中寻找凌星特征,来判断是否存在系外行星,仿真实验表明1维卷积神经网络性能较高;Shallue等[5]利用实测光变曲线和结构更复杂的深度神经网络,从开普勒卫星数据中发现了两颗新系外行星.在判别空间碎片基本类型方面,Howard等[6]使用模拟光变曲线训练多种机器学习模型,对目标形状和稳定性的分类结果显示随机森林算法表现最佳,但文章没有使用深度神经网络等更先进的算法,且形状分类中还夹带了稳定性分类,而对稳定性显然有其他更简单、有效的方法进行分类;Linares等[7]和Furfaro等[8–9]基于深度卷积网络,对空间目标光变曲线进行了仿真和实测实验,虽然仿真光变包含了9种类型的目标,但部分类型与目标实际形状差别较大,并且仿真中初始姿态和角速度都是统一的,导致实验实用性较差.实测实验对3类空间目标进行分类,数据集未事先区分旋转目标与稳定目标,并且直接从光变曲线中提取500个点作为训练数据,并未作其他优化.

本文同样基于光变曲线和深度神经网络,探讨对空间碎片的基本类型进行分类.为了聚焦碎片类型分类,首先应区分碎片的旋转运动状态,旋转碎片的光变曲线与稳定碎片差别巨大,应各自开发相应的分类方法,本文关注旋转碎片的分类.光变曲线作为输入特征应当被适当改造和优化,使得各条数据的特征在时域上拥有可比性,由于本文只关注旋转碎片,因此截取1个自转周期的光变曲线(也称为相或相曲线)作为训练数据,并在最亮处对齐.本文仿真实验将测试深度卷积神经网络的分类效果,并和其他机器学习算法进行比较,实测实验尝试对火箭体和失效卫星进行2分类,并尝试对数据较多的碎片进行子类别的区分.

第2节简单介绍深度神经网络算法,包括1维卷积层和全连接层的工作原理;第3节给出模拟光变曲线的生成方法、4种碎片外形和材料参数的设定等,还介绍实测光变曲线的提取方法、数据分布特征等;第4节为仿真实验部分,包括实验步骤、模型参数调优过程、分类的结果以及模型学习曲线的特征,并且给出了与其他机器学习算法的比较;第5节为实测实验部分,分别介绍2分类实验和型号分类实验结果.

2 深度神经网络

本实验中深度神经网络主要包括卷积层(Convolutional Layer)和全连接层(Fully Connected Layer)两种结构.卷积层各神经元有限连接,增强对局部特征的学习.由于输入层是光变曲线,本文卷积层为1维单通道,基本原理如图1(a)所示,输入层分别同多个滤波器(卷积核)进行卷积运算后经过池化层输出,1维卷积运算公式为:

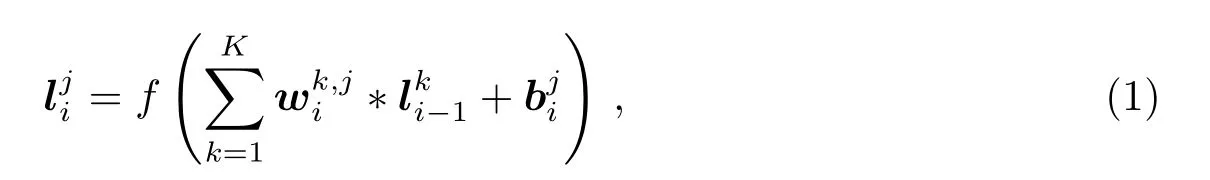
其中K为i−1层特征图总数,为上一层输入,表示第i−1层的第k个特征图,表示第i层生成第j个特征图的第k个卷积核向量,为第i层第j个特征图的偏置量,为第i层的第j个特征图,∗表示离散卷积运算,还涉及步长和边界处理等,f为激活函数,本文使用relu函数(recti fied linear unit function),即f(x)=max(0,x).卷积层之后常使用池化层降低模型参数个数,即在原特征图内依次进行欠采样,在减少后续计算量的同时让特征图具有一定的平移不变性,突出某个特征是否存在而非特征的准确位置,本文使用最大池化层(max-pooling layer).

图1 深度神经网络中的卷积层和全连接层(a)1维卷积层、(b)全连接层Fig.1 Deep neural network(a)1D convolutional layer,(b)fully connected layer

全连接神经网络一般由输入层、若干隐含层和输出层组成,如图1(b)所示,除独立使用外,还常作为卷积网络的后端使用.在每个神经元上,输入数据与权重相乘后再加上偏置项,最后经激活函数输出,用公式表示为:

其中li−1为上一层输入向量,Wi为权值向量,bi为偏置向量,li为i层的输出向量.特征向量由输入层依次向下传递,通常最后使用softmax函数计算多分类问题概率,即

其中S表示softmax函数,xm表示输出层第m个节点的输出值,N为输出层节点总数,通过将概率归一化使得各类别概率之和为1.对于多分类问题,通常使用交叉熵(Cross-Entropy)损失函数作为优化目标,记为lossCE,即

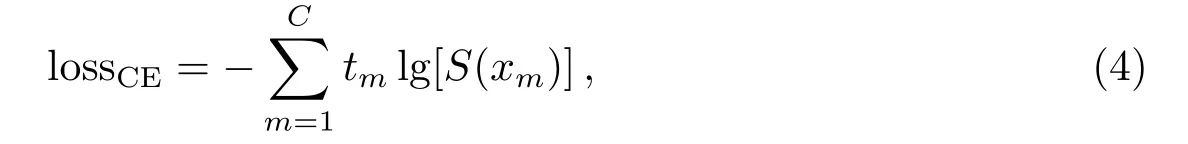
其中C为类别总数,t=[t1,t2,···,tC]为分类结果的目标向量,即真实标签.

本文深度神经网络算法基于Python语言下Scikit-learn、TensorFlow、Keras等软件包实现,其官方网站上有丰富的说明文档和应用实例,作为代码开源且容易上手的深度学习工具,在许多领域广泛使用.

3 训练数据集

使用深度神经网络解决分类问题需要制备训练集,好的训练数据应该与测试数据特征相似,并且在参数空间内分布均匀.本文分别进行了仿真和实测实验,其中仿真实验使用模拟光变曲线,优点是数量多、覆盖全,缺点是仿真建模精度有限;实测光变虽然真实,但由于数据量有限,存在覆盖不全、分布不均的问题.实验中每条光变曲线长度设定为1个自转周期,并均匀采样200个点.

3.1 模拟光变

本文空间碎片光度模型的双向反射分布函数(Bidirectional Re flectance Distribution Function,BRDF)使用文献[10]中的Cook-Torrance模型.对于快自转碎片或高轨道碎片,1个自转周期内观测相位的变化幅度较小,仿真时忽略了碎片的轨道运动,并使用平面转动模型.生成模拟光变曲线的过程如下:

(1)设定仿真目标的形状和各个表面材料的BRDF参数、自转轴指向等;

(2)设定观测相位角为70◦,根据旋转运动模型得到每个光度采样点上的坐标系转换矩阵;

(3)将碎片表面分成若干结构面,给定每个结构面的形状参数,BRDF参数在给定范围内随机选择,再把每个结构面分割为若干微面元分别计算反射流量,最后累加所有面元的流量;

(4)每个种类模拟2500条光变,在流量最大处对齐光变曲线,并归一化到1000 km斜距.

仿真实验中,空间碎片被大致分为如下4类,参见表1,(sCT、dCT、ωCT、mCT)为Cook-Torrance模型主要参数,分别表示镜反射系数、漫反射系数、漫反射反照率和均方根斜率,仿真中总是令sCT+dCT=1.圆柱形镜反射碎片类型包括早期的高轨通讯卫星,由于表面覆盖太阳能电池板因此被认为以镜面反射为主,此外据报道部分火箭体表面为金属材料,也应以镜反射为主;漫反射圆柱体用来模拟大部分火箭体,表面涂有白漆等材料,通常认为以漫反射为主.Box-wing形状卫星是指本体大致为正方体并带有两个对称太阳能帆板的卫星,帆板的正反面都应以镜反射为主,卫星本体难以建模,考虑到部分器件覆盖保温材料,而保温材料被认为以镜面反射为主,因此设定Box-wing卫星为镜反射类型;立方星表面除了部分覆盖太阳能电池板外,其他部分较为复杂,模拟中简化为镜反射平面.其他的碎片表面复杂难以建模,但可能在一定程度上类似于上述某种类型.

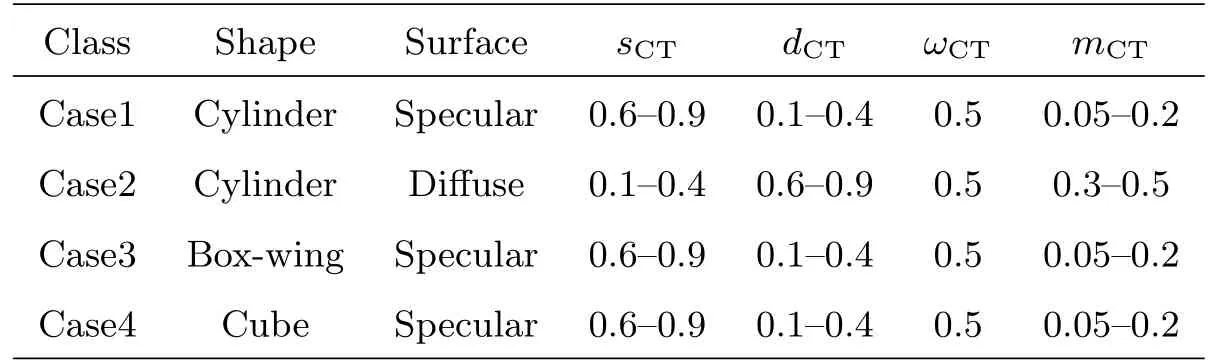
表1 各种类碎片对应的BRDF参数范围Table 1 The BRDF parameter ranges of the de fined space debris

仿真中碎片尺寸的设定包括:以某款火箭体的真实尺寸(长:12.38 m,直径:3.0 m)定义漫反射圆柱.为了考察相似设定下模型的分类准确率,对镜反射圆柱也采用了相同设定,Box-wing卫星本体设定为1 m×1 m×1 m,帆板法方向指向x轴,尺寸为1 m×4 m并忽略厚度.同样为了考察有无帆板对分类结果的影响,立方星采用Box-wing卫星本体的尺寸.表面材料BRDF参数的设定参见表1.仿真中遮挡和多次反射/散射被忽略,事实上对于火箭体,上述效应影响很小;对于常规卫星,遮挡一般发生在帆板和卫星本体之间,在产生遮挡的观测几何上往往仿真精度也较差,因此仿真中忽略遮挡效应;由于卫星上多个部件往往有强烈的镜面反射,多次反射效应会对仿真结果产生影响,为加快仿真计算速度,本文忽略了多次反射效应.空间碎片的尺寸仅作为参考,需要注意的是尺寸的缩放仅仅反映在光变曲线整体上下平移,对光变曲线的特征影响不大.

3.2 实测光变

实测光变曲线从公开的MMT(Mini-Mega TORTORA)数据库1http://mmt.favor2.info/satellites中提取,其望远镜系统由安装在5个赤道仪上的9个独立通道组成,每个通道视场9◦×11◦,并使用sCMOS(scienti fic Complementary Metal-Oxide Semiconductor)相机作为终端,系统主要科学目标是大视场高分辨率时域天文巡天观测,同时空间目标的光度信息也被记录了下来.截至2019年10月,数据库记录了超过3600个空间目标的光变曲线,主要分布在低轨和椭圆轨道上.由于MMT均采用极短曝光模式,帧频一般为10 fps,极限星等通常为10等左右,只能观测到较亮目标.经过“具有周期性”和“失效卫星或火箭体”两个条件筛选后,本文选择了数据量较多的几类碎片,其中火箭体按照型号名称归类,观测弧段较多的是如下7类:Atlas(宇宙神)、CZ3(长征3号)、Delta4(德尔塔4型)、Falcon9(猎鹰9号)、H2A(H系列2A型)、惯性上面级(Inertial Upper Stage,IUS)、极轨卫星运载火箭(Polar Satellite Launch Vehicle,PSLV);失效卫星按照平台类型(Bus Type)归类,观测弧段较多的是如下3类:Globalstar(低轨通信卫星星座)、Iridium(铱星系列)、Tiros(一类卫星平台的总称).

从MMT原始数据中提取训练集的方法如下:

(1)从MMT网站下载目标的光度数据文件和周期信息文件(其中周期信息为MMT团队计算的每个弧段光变周期的值,其精度较高,一般可以直接使用,本文重新计算了光变周期并重点检查了计算的周期是否和真实周期存在倍数关系),剔除地影中的和少量多色测光数据;修正原始光度到1000 km距离,但并不做相位角改正;

(2)利用Lomb-Scargle谱分析方法计算光变曲线的候选周期,剔除周期性不显著的弧段,再通过光变曲线折叠方法在候选周期、1、2、4倍附近微调,寻找最佳周期;计算最佳周期折叠后的离散程度,决定周期提取是否成功,对于火箭体,还可使用双峰拟合方法检验周期提取结果;

(3)每个弧段每隔2–3个周期提取1次相曲线,对于缺失部分大于半周期的光变曲线,判断是否为火箭体,如果不是则剔除;用最佳周期折叠后,利用滑动中值滤波器或者Savitzky-Golay滤波器平滑原始曲线,并插值到200个均匀采样点,窗口内光度标准差的均值作为光度提取误差,记为Eex,即Eex=mean[std(Mb)],b=1,2,···,B,其中std为求标准差函数,mean为求均值函数,B为窗口总数,Mb表示第b窗口内的光度数据.

通过上述方法,本文从MMT数据库中共提取了11237条火箭体光变曲线,19204条卫星光变曲线.不同应用场景对光变曲线的精度要求不同,例如在基本形状2分类问题(火箭体或失效卫星)中,可以使用光度提取误差3σ判据内的数据;而对同一类型碎片进一步分类问题中,本文使用2σ判据.图2分别为所有火箭体和失效卫星的光度提取误差分布,左图火箭体的分布比较对称,而右图失效卫星分布的歪斜(Skewness)较大,因此使用χ分布分别做拟合,拟合结果见表2.从拟合参数可以看出,由于火箭体光变曲线形状往往更简单,其光变曲线提取精度整体好于失效卫星,误差均值分别为0.19、0.27.以基本形状2分类问题为例,本文使用提取误差小于0.39的火箭体相曲线和误差小于0.66的卫星相曲线.

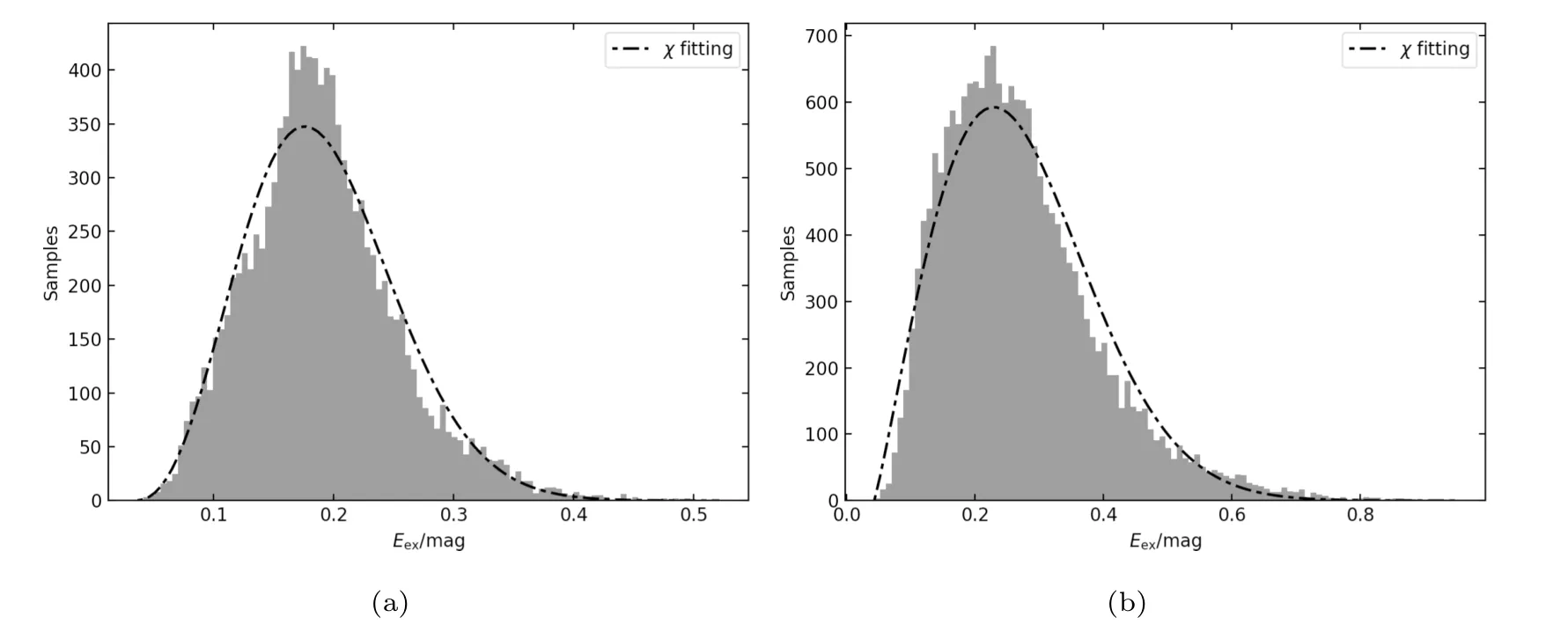
图2 实测光变提取误差的χ分布(a)火箭体、(b)失效卫星Fig.2 The χ distribution of extracted errors for observed light curves(a)rockets,(b)satellites

表2 实测光变提取误差的χ分布拟合参数Table 2 The fitting parameters of χ distribution of extracted errors for observed light curves

4 仿真实验

本文利用深度神经网络进行空间碎片基本形状分类的步骤包括:(1)制备有标签的训练集和测试集,仿真数据训练集和测试集按2:1划分,理想的训练集和测试集应较为均匀地覆盖所有种类的样本,仿真数据不存在这个问题,对于实测数据若某种类样本数过少,本文使用数据“复制”作为补救,例如对原样本平移或加噪等生成新的同类样本,但“复制”数据应当仅占样本的较小部分,否则会产生特征冗余的数据集;(2)将数据集输入神经网络之前,标准化输入特征,使特征总体均值为0、方差为1;使用one-hot方法对样本标签编码,标签对应位置的向量元素为1,其余均为0,此时网络的输出层神经元数量和种类数相同;(3)设定神经网络模型参数、损失函数、优化算法等,然后输入训练集,设置批处理大小、迭代次数之后开始训练网络,本文迭代次数设定为100;(4)根据训练集损失函数和准确率随迭代次数的变化曲线,判断模型收敛和拟合效果;将测试集输入训练好的网络中,测试集准确率可以反映模型的泛化能力,confusion matrix表示模型对各种类数据的分类能力;(5)本文使用不同的随机数种子重复上述步骤10次,然后给出平均化的模型输出.

4.1 模型参数调优

在使用机器算法时需要设计合适的网络结构、配置、参数等,称之为模型参数调优.此外,将分类问题描述和构造成适用于深度神经网络的形式也同样重要,包括特征提取、数据预处理等.仿真实验中被优化的模型参数包括滤波器数量( filter number)、卷积核尺寸(kernel size)、输入层欠采样率(binning)以及模型深度(model depth)等.实验中用于对比的基础模型较浅,从上到下依次为卷积层、卷积层、dropout层、池化层、全连接层、全连接层、softmax层.初始参数为:卷积核尺寸为64×3×1,步长为1,dropout系数为0.5,池化步长为2,全连接层神经元数量依次为500、100,使用relu激活函数和adam优化器,损失函数为上述多分类交叉熵函数,批处理大小为32.

图3是参数调优结果的统计,图中横轴表示不同的参数取值,纵轴表示模型对测试集分类的准确率,箱线图的虚线表示在这一参数取值下多次训练统计结果的中值,矩形上下边表示25%和75%分位数,圆圈表示1.5倍4分位距之外的点,短横线表示1.5倍4分位距之内的极值.对滤波器数量的测试结果如图3(a)所示,每个卷积层都有多个滤波器,随机初始化后模型每次训练会调整滤波器的值.滤波器作用是滑动卷积上一层特征图,得到这个滤波器对应的特征识别图.滤波器数量越多意味着可以在更高维度的特征空间进行特征提取和识别,但对具体问题并非越多越好,且训练时间也是需要考量的因素.在基础模型其他参数不变的情况下,本文测试了每层滤波器个数分别为8、16、32、64、128时模型对仿真数据的识别率,可以看出,8和128对应的结果较为离散,且整体识别率较低,16对应的结果较为集中但中值略低于其余参数,整体来看滤波器数量设为32或64的效果最好.考虑到基础模型使用了较浅的网络,调优后网络深度和复杂度可能增加,最后选择滤波器数量为64.

对卷积核大小的优化结果如图3(b)所示,卷积核大小决定了特征提取的尺度,小尺寸对微小特征敏感,但无法直接感知跨度较大的特征,随着卷积层的堆叠以及池化层的加入,即使使用小尺寸卷积核也可以感知原始输入中大尺度的特征,因此在图像识别领域,往往增加网络深度并使用小尺寸卷积核.需要注意的是,卷积核大小同输入层binning操作是相互影响的,此次试验输入层特征向量未做binning,即大小为1×200,在此基础上实验测试了卷积核大小为2、3、5、7、11时模型的准确率,结果表明卷积核大小为5时,分类准确率的中值以及整体分布达到最佳.

对输入层binning的测试结果如图3(c)所示.我们总希望在分类准确率基本不变的情况下尽量减少训练时间,对输入的光变曲线进行欠采样可以降低输入层维度,大大降低计算量,缺点是可能会破坏局部微小特征.为此实验测试了数据binning从1到5时模型的准确率,结果显示在各个参数下模型的表现差别不大,尤其是整体的分布情况基本在同一水平线,考虑到调优后的网络深度和复杂度可能增加,输入数据维度太低会限制模型深度,最终确定对输入数据不做binning,因此前面卷积核大小的优化结果依然有效.

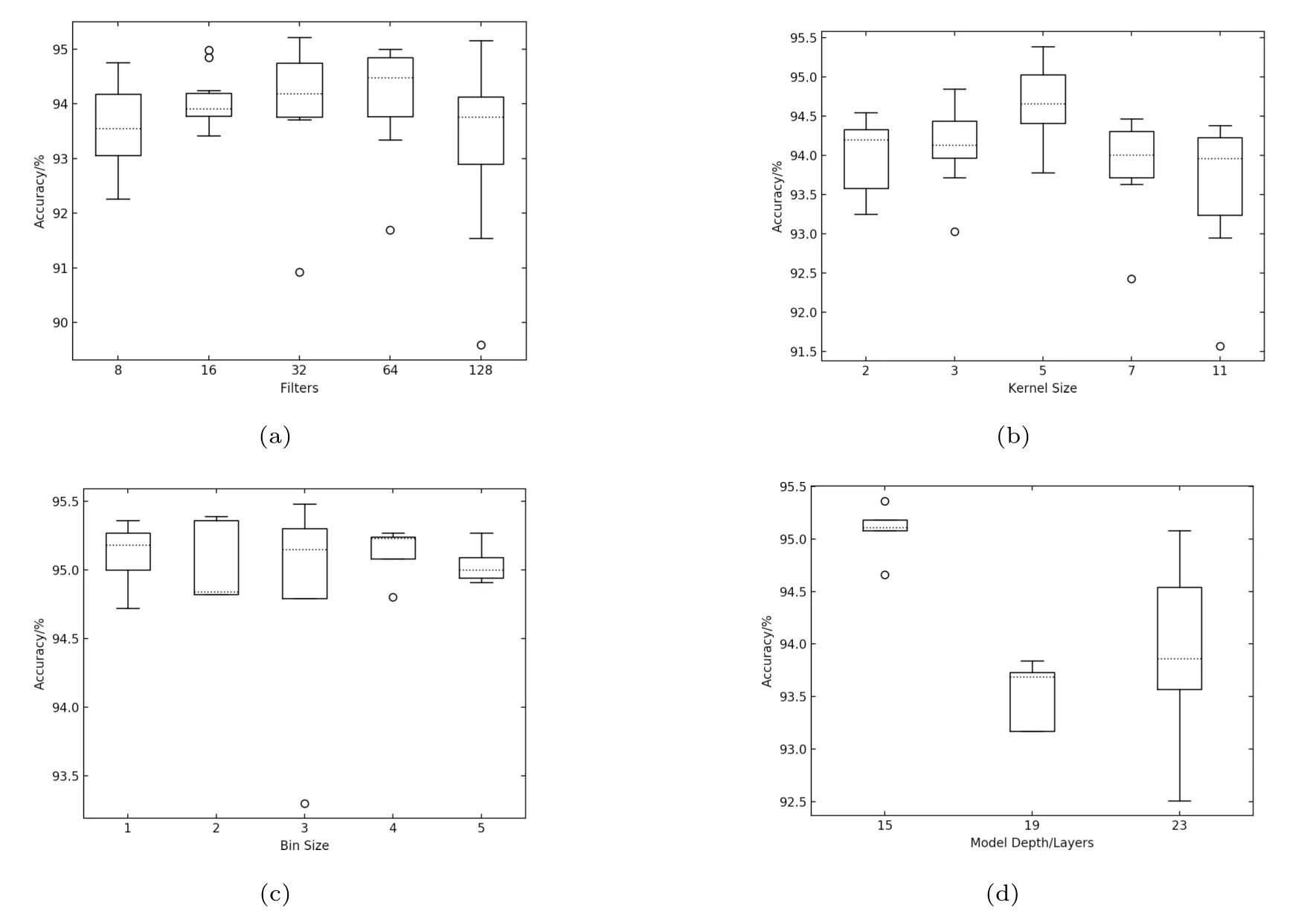
图3 深度卷积网络的模型参数优化(a)滤波器数量、(b)卷积核大小、(c)欠采样率、(d)模型深度.Fig.3Hyperparameter tuning for Deep Convolutional Network(a) filter number,(b)kernel size,(c)bins,and(d)model depth.

最后测试了模型深度对训练结果的影响,如图3(d)所示,如果把两个卷积层、1个dropout层和1个池化层的组合看作1组卷积层,则3、4、5组卷积层对应了深度为15、19、23层的网络结构,本文设置每组卷积层的参数都是一致的,测试结果显示,使用3组卷积层的效果明显好于更深的网络,分类准确率大致在95%以上.综合上述所有参数优化的结论,本文最终使用滤波器数量为64、卷积核大小为5、输入层特征维度为200、深度为15层的网络模型.

4.2 分类准确率

不同类别的分类准确率可以由confusion matrix直观表示,如图4所示,其中cyl-s、cyl-d、bow-w、cube分别表示镜反射圆柱、漫反射圆柱、Box-wing卫星和立方星.每个方格数值表示相应横轴的真实类别被识别为纵轴预测类别的概率,总的分类准确率为95.5%,图中显示镜反射和漫反射圆柱的识别率都是100%,尽管两者形状尺寸完全一致,但材料反射特性的差别可以将其区分,这说明常规火箭体可以较容易地通过光变曲线进行识别,无论其表面是否涂有白漆或是光滑金属材料;Box-wing卫星和立方星的识别成功率分别为89%和93%,其中10%的Box-wing卫星被误分类为立方星,而6%的立方星被误分类为Box-wing卫星,原因是仿真中将立方星尺寸放大到跟Box-wing卫星本体相当,且表面都设定为镜反射特性,导致两者的特征相似性过高.

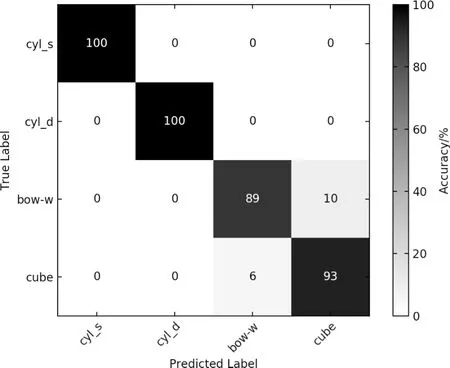
图4 仿真实验中4种碎片分类结果confusion matrixFig.4 The confusion matrix for the results of 4 types of debris in simulation experiments

4.3 学习曲线

在神经网络的训练过程中,根据每次迭代后模型对训练集(实际上是训练集的一部分)和测试集的分类准确率,可以评估模型更新迭代的效果,这些随训练次数变化的曲线被称为学习曲线.对训练集的学习曲线表示模型学习程度的变化,对测试集的学习曲线则表示模型泛化能力的变化,即模型对未知数据的预测能力.根据学习曲线的收敛速度可以给出训练迭代次数的合理估计,当学习曲线基本不再变化时,表明模型已经无法学习到新知识,此时可以中止训练;而当训练中止时准确率曲线仍在上升或损失曲线仍在下降,表明模型欠拟合,还应继续训练.训练集和测试集学习曲线的差异反映了模型过拟合的状况,如果测试集准确率已经基本收敛到较大值甚至不升反降,而训练集曲线仍然上升,表明模型过拟合,泛化能力较差;当训练集和测试集的损失曲线同步下降但总是存在较大间隔时,可能原因是训练集的代表性不够,也就是训练集难以提供足够信息让模型正确识别测试集中的分类特征,这经常出现在几个类别的特征非常相似的情况下;如果学习曲线出现明显震荡,可能与分类问题数据集本身有关.

仿真实验的学习曲线如图5所示,实线代表训练集,虚线代表测试集.从准确率曲线可以看出,训练集准确率持续上升,在迭代100次后超过98%,但测试集准确率上升趋势不明显,停留在95%左右,这表明虽然模型持续从训练集中学习到新知识,但这些知识对测试集分离不起作用,即模型过拟合、泛化能力差,从损失曲线中也可以得到相同结论.此外,曲线存在明显的震荡也说明数据集在设计上不够理想,某些特征区分度可能较小,分类结果的偶然性较大.

图5 仿真实验的学习曲线(a)准确率曲线、(b)损失曲线.Fig.5 The learning curves of simulation experiments(a)accuracy curves,(b)loss curves

4.4 与其他机器学习算法的比较

作为对比,本文使用同样的数据集测试了其他机器学习方法的分类准确率,包括K近邻(K-Nearest Neighbors,KNN)、决策树(Decision Tree,DT)、支持向量机(Support Vector Machines,SVM)和随机森林(Random Forest,RF).需要注意的是,这些机器学习方法通常使用有序列的特征作为输入,也就是缺乏对输入向量平移不变性的支持,而利用光变曲线识别空间碎片基本形状需要考虑特征的平移不变性,可能的解决办法包括两类:(1)是在时域上对齐光变曲线,本文采取在最亮处对齐的方法,然后还可以利用主成分分析(Principal Component Analysis,PCA)方法进一步降低特征维度;(2)是将时序信号转换到频率域上,初始相位以外的其他参数是原信号的平移不变性参数.本文使用第1种方法,将初始特征维数为200的光变曲线通过PCA提取前12项主要成分,可以表示97.64%的原始数据特征.

本文使用Scikit-learn程序包实现上述机器学习算法,对每种算法的关键参数进行了简单调优,结果为:KNN的K值为5,DT中分割判断函数为gini,SVM中C值为1,kernel为径向基函数,RF中estimators数量为100.最终对优化后的模型使用Bootstrap方法划分训练集和测试集,准确率统计结果见图6,虚线表示统计结果中值,矩形上下边表示4分位距,短横线表示数据上下限.KNN算法的准确率在93%左右,DT算法仅91%左右,是所有测试方法中最差的.SVM和RF算法的准确率相当,在94%–95%,说明对于本文分类问题这两种算法也是较好的选择,这也是后续型号/平台分类实验中选择RF算法的原因.CNN的准确率最高,超过了95%,因此本文使用深度神经网络算法识别空间碎片的基本形状.

图6 不同机器学习算法的分类准确率Fig.6 Accuracy comparison of di ff erent machine learning algorithms

5 实测实验

5.1 2分类实验

由于实测光变数量较少且分布不均,本文先探讨基本的2分类问题,即判别碎片类型是火箭体还是失效卫星.从实测数据集中随机各选择2500条相曲线,并使用仿真实验中的7层基础模型,利用Bootstrap方法训练100次,分类结果见表3,分类结果准确率的均值为99.31%,中值为99.35%,3σ置信区间为(97.60%,99.83%).火箭体的识别率为99.24%,略低于卫星识别率99.50%,实验结果表明针对本文提取的实测光变曲线,深度神经网络可以较准确地区分火箭体和失效卫星.需要说明的是,上述实验建立在少量类型碎片的实测数据上,有明显的选择效应,很多空间碎片的形状与实验样本相差很大,更大规模的形状分类结果可能会有所不同,受可获取实测数据数量和分布的限制,在本文研究范畴内无法覆盖更多碎片,因此利用这些数据进一步区分碎片类型存在很多局限性.尽管如此,本文选择了实测数据相对较多的几类火箭体和卫星,尝试进行碎片型号(或卫星平台)识别.

表3 火箭体和卫星实测数据2分类准确率Table 3 The accuracy of binary classi fication for satellites and rockets

5.2 型号分类实验

每个类型的相曲线数量见表4,由于数据集较小,实验放弃深度卷积网络而选用随机森林算法,且要求每个类型的数据集含有500个样本,然后分别对火箭体和卫星型号进行分类实验.火箭体中CZ3、Atlas、H2A和Falcon9的数量均超过500条,分别随机选择规定数量的样本;Delta4数据有352条,使用数据“复制”方法,对相曲线加入均值为0、标准差为0.5星等的高斯噪声,再平移0.5个相位,生成新的样本,使得总数达到500条的要求;对于IUS和PSLV,由于数据量过少,上述方法更倾向于产生特征冗余的数据集,不应再作为分类选项.因此火箭体型号识别实验中,仅设定了Atlas、CZ3、Delta4、Falcon9和H2A 5类.

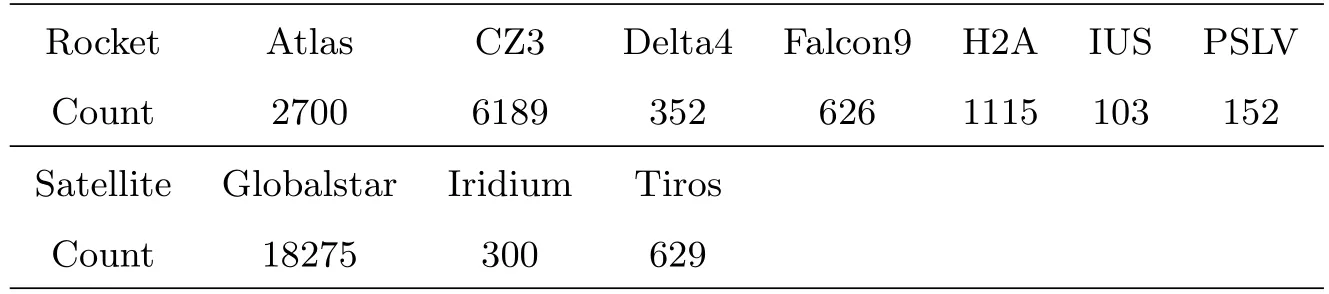
表4 实测光变曲线数量分布Table 4 The population distribution for extracted observed light curves

对失效卫星,绝大多数相曲线都来自37颗Globalstar卫星,它们都处于旋转状态,周期从几秒到一百多秒不等;Tiros平台包含若干系列的卫星,不同系列的形状可能存在差异,但应当大致相同;Iridium系列卫星由于相曲线数量只有300条,同样使用“复制”方法扩充样本.因此卫星平台分类实验中包括Globalstar、Tiros和Iridium 3类.

训练集和测试集按3:2比例划分,使用Bootstrap方法重复实验100次,表5是识别准确率的统计,整体看火箭体的分类准确率在85%左右,3σ置信度区间为(82.60%,88.73%),明显低于卫星的分类结果,后者的准确率在93%左右,3σ置信度区间为(88.98%,96.20%).分类结果符合预期,即火箭体由于形状大多类似圆柱体,光变曲线通常为双峰结构,在形态上差异相对较小,因此分类难度较大;而实验中3类卫星在外形上区别明显,光变曲线也更复杂,可以提供更多的特征用于分类.

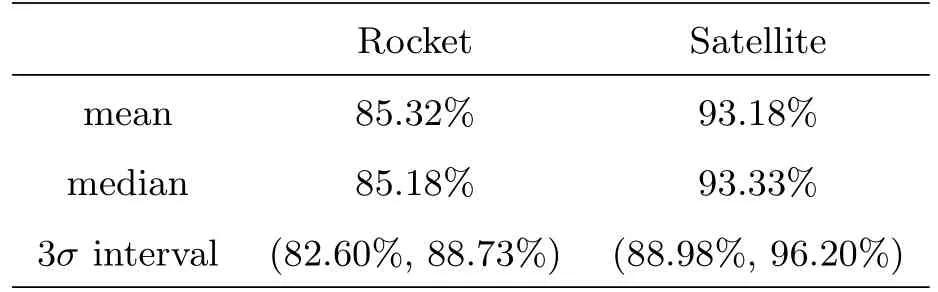
表5 碎片型号分类实验的准确率Table 5 The classi fication accuracy of space debris types

分类结果的confusion matrix如图7所示,火箭体中除了Atlas,其余的识别率都高于80%,其中最高的是Delta4和H2A,真实图片显示它们并非完全类似于圆柱体,而是由上面一段圆柱加下面椭球形储箱组成,相对复杂的结构会在光变曲线中表现出更多特征,有利于提高识别率,同时由于两者之间外形相似,增加了混淆概率;Delta4和H2A的相互误分类概率之和达到17%,是所有组合中最高的.相互误分类概率较高的另外一组CZ3和Falcon9,它们都是传统的长圆柱体形状,且通常表面都涂有白漆.

卫星平台分类结果表明,识别率最高的是Tiros,其次是Iridium,需要注意的是Globalstar和Iridium相互之间区分度较高,而Tiros与其他两类的相互误分类概率明显较大.Globalstar形状类似于Box-wing卫星,而Iridium和Tiros形状都高度不规则,相互间的识别率反映了碎片形状的相关性.

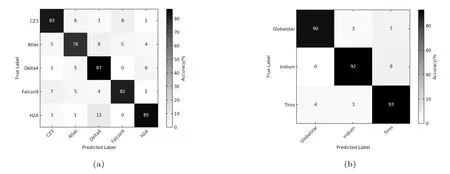
图7 碎片型号/平台类型分类结果的confusion matrix(a)5种型号火箭体的分类结果、(b)3种平台失效卫星的分类结果.Fig.7 The confusion matrix for the classi fication results of space debris types/bus-types(a)5 types of rockets,(b)3 bus-types of satellites.

6 总结与展望

本文探讨了基于光变曲线的空间碎片基本形状分类方法,利用深度神经网络对碎片基本形状以及进一步的型号/平台分类进行了仿真和实测研究.

仿真实验设置了漫反射圆柱、镜反射圆柱、Box-wing卫星和立方星4种类别,深度卷积网络分类准确率为95.5%,其中对漫反射和镜反射圆柱的识别率明显高于Boxwing卫星和立方星.还测试了K近邻、支持向量机、随机森林和决策树算法在本文分类问题上的表现,结果显示深度卷积网络效果最好,随机森林、支持向量机算法次之.在实测实验中,从MMT数据库中提取了Atlas、CZ3、Delta4、Falcon9、H2A等火箭体和Globalstar、Iridium、Tiros 3种卫星的光变曲线,在火箭体和卫星2分类问题中,利用深度卷积网络和Bootstrap方法得到的分类准确率3σ置信区间为(97.60%,99.83%).此外,本文使用随机森林算法进行了碎片型号或平台分类,对火箭体型号的分类准确率3σ置信区间为(82.60%,88.73%),其中H2A和Delta4的相互误识别概率之和为17%,Falcon9和CZ3的相互误识别概率之和为15%,表明它们之间均存在较高的相似性.3种卫星平台的分类准确率3σ置信区间为(88.98%,96.20%),结果显示Globalstar和Iridium的区别更明显,而Tiros同另外两类的误分类概率较大.

本文仿真实验仅设定了4类碎片,且简化处理了形状和反射特性参数,实际上空间碎片种类繁多且结构复杂,仿真实验的局限性显而易见,对于复杂碎片,给出宽泛的形状估计也是值得讨论的.此外对复杂碎片的建模更困难,除了形状和材料信息不易获得外,也难以用简单模型去描述旋转运动,因此难以生成仿真数据集.本文下一步计划增加碎片仿真的种类,并测试随机模拟碎片的识别率问题,期望给出更大范围的碎片基本形状分类结论.此外空间目标地面光度仿真实验室可以给出大批量的空间碎片模拟光变曲线,其仿真精度较高,我们计划利用实测数据结合高精度仿真数据建立训练集,实现对实测发现的未知目标正确分类.