主反射面变形引起的天线指向误差修正方法∗

梅庚君12 项斌斌2 王 娜2 王兆军1

(1新疆大学物理科学与技术学院乌鲁木齐830046)(2中国科学院新疆天文台乌鲁木齐830011)

1 引言

天线的指向误差分为伺服控制子系统误差和天线结构子系统误差两部分.对于影响指向精度的众多天线结构子系统因素,本文着重考虑主反射面变形引起的指向误差问题,目前主要考虑的作用在天线结构上的环境载荷有重力、风和热效应[1].环境载荷引起天线的主面结构变形进而导致指向偏差的关系示意图如图1所示,天线的实际指向已经偏离了目标星源.将环境载荷作用下实时响应主面变形的实际天线指向称为结构指向,完全理想环境下的天线指向命名为参考指向.

一般的天线指向系统偏差数学模型的建立往往依赖于配置在天线物理顶点处或其它平台处的经纬仪、准直仪、陀螺仪等测量仪器[2],且普遍考虑的是轨道不平度和天线座架变形引起的方位轴不垂直[3–4]、方位轴俯仰轴不正交[5]、副反射面调整机构误差引起的机电轴不重合等一系列作用于指向误差的天线结构子系统误差因素[6],但实测中无法实现对天线主面变形的实时全局观测.在主流的射电天线主动面技术之外[7],很少有对天线主反射面变形这一误差因素的关注.另一方面,已有的数学模型并未对主面变形所引起的指向误差做有效表征.本文提出一个简便的指向修正数学模型,能够应用于环境载荷作用下实时响应主面变形引起的天线指向误差精准补偿系统的建立.

图1 环境载荷作用下的天线指向偏差Fig.1 Antenna pointing deviation under environmental load

2 基于型面吻合的天线结构指向误差预测

2.1 反射面坐标系统

为了更清楚地表示主面变形后天线所匹配的结构指向,建立了如图2所示的天线反射面坐标系统.当射电望远镜主反射体指向仰天位置时,反射面坐标系统中的XOY平面平行于水平面.坐标系统中的X轴满足与天线俯仰轴的轴线平行的关系,Z轴由天线的物理顶点出发过参考焦点,即对应理想环境工作条件下天线的参考指向.反射面坐标系统的XOY平面随天线俯仰角的变化与水平面有一夹角,且该夹角始终与天线俯仰角互余.

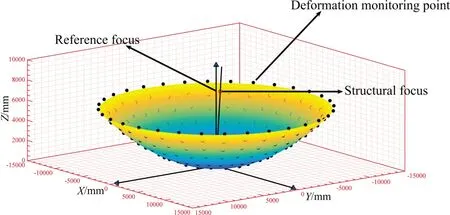
图2 天线反射面坐标系统Fig.2 The coordinate system of Antenna re flector

当利用经纬仪、全站仪等测量仪器结合靶标对变形主面进行空间坐标测量采集时,需要根据反射面弧长、周向间距和反射面径向形状等天线结构固有参数建立反射面坐标系统和测量坐标系统之间的空间转换关系.上述工作在射电天线指向天顶角时[8]进行最为便利,也更加准确.

2.2 3自由度型面吻合

从上世纪90年代到本世纪初,伴随计算机运算速度的巨大提升与功能函数的不断丰富,相关型面吻合方法的发展也趋于完善.按型面吻合最小量的选取原则进行分类,这些方法大体上可以概括为两大类:

(1)一般形式的型面吻合最小量:法向偏差[9]、轴向偏差[10],可以基于上述两种型面吻合最小量和线性最小二乘原理,利用矩阵的逆,对矩阵法方程进行直接求解;对于同天线增益直接相关的半光程差[11],可换用非线性最小二乘原理,基于Gauss-Newton法进行迭代求解;

(2)特殊形式的型面吻合最小量:误差方程.例如特征值吻合[12],基于间接平差原理由一般2次曲面方程形式给出误差方程,对系数进行迭代改正并表征为矩阵方程的形式,最后利用2次项系数矩阵的特征根矩阵和特征向量矩阵做最佳型面吻合;基于刚体位移思想吻合[13],以旋转抛物面的矩阵形式给出误差方程,利用间接平差原理和非线性最小二乘的方法,任取初值进行迭代求解.

本文结合20世纪70年代Ruze[14]提出的射电天线增益公式,选取由型面几何定义和光学性质直接计算得到的半光程差作为最小量进行最佳吻合.

2.2.1 半光程差的直接计算方法

图3以抛物面天线为例,从焦点F发出的波,到达理论面上任意点A和P1,经过反射分别抵达等相位面上的点A′和P1′,则有:

其中,L为从焦点到等相位面的光程.假设反射面在点P处凸出(凹陷的情况下类似),电磁波经由该点反射到达等相位面上点P′,点P和点P1分别对应准面上的点M和点M′.同时,ρ对应点P和点P1之间的距离值,∆对应点P和点P1分别到Z轴的两条垂线之间的平行距离.则从焦点F射向点P到达等相位面上的电磁波所经过的光程与L之间的差值就是所谓的光程差,记作2δ.从图3可得:

由于圆锥曲面良好的光学性能,在天线设计中经常采用抛物面作为主面.根据圆锥曲线的轨迹定义:到定点的距离与到定直线的距离之比为常数e可知,当e=1时为抛物线有(图3):

又根据抛物线的光学性质:反射波都平行于抛物线的轴射出,可以得到在凸出点P处有,代入(2)–(3)式即可得到抛物面半光程差直接计算公式:

2.2.2 吻合对象

本文的研究对象是旋转抛物面型大口径反射面天线,标准旋转抛物面是由抛物线绕对称轴(焦轴)旋转而成,其空间坐标系下的标准方程为:

式中,r为天线口面半径,f为天线焦距值.

2.2.3 3自由度最佳吻合原理

旋转抛物面天线因为其结构的特殊性:关于主轴(反射面坐标系统下的Z轴)对称,在型面吻合时绕该轴的旋转量可视为零.另一方面,考虑到反射面天线物理顶点附近刚性极好,同时主面各部形变是极其微小的,最终略去吻合时所涉及的空间3平移自由度(均视为零),仅保留余下的3个自由度:绕X轴的旋转量γ,绕Y轴的旋转量φ以及一个新的旋转抛物面的焦距值f.根据吻合特点,将其命名为型面定顶吻合法,吻合原理示意如图4所示.

图3 抛物面的半光程差Fig.3 Half optical path di ff erence of paraboloid

图4 3自由度最佳型面吻合Fig.4 Best fit based on three degrees of freedom

2.2.4 型面定顶吻合算法

假设反射面坐标系统下天线主面上离散形变点坐标为(x,y,z),形变测量点对应的最佳吻合面上的吻合坐标值为(xm,ym,zm),其中m为主面形变点采集数目.对形变点坐标做基于半光程差的型面吻合,将R的转置作为旋转变换矩阵,具体形式如下:

形变测量点坐标到吻合点坐标的转换关系为:

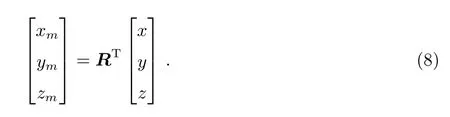
结合图2所建立的反射面坐标系统以及图3所示的抛物面半光程差解算原理示意图,天线的焦点理论坐标为(0,0,f),其准线绕Z轴旋转成的平面为z=−f,根据(4)式和(5)式直接列出基于半光程差的型面吻合最小量表达式,并用δ表示:

将上述型面吻合问题转化为非线性最小二乘问题:

其中,s=[γ φ f],采用Gauss-Newton法解决该非线性问题.主要迭代过程如下:

其中,k为循环迭代次数,

2.2.5 主反射面变形对天线结构指向的影响

求得s=[γ φ f],则反射面坐标系统下吻合焦点的空间坐标值为:

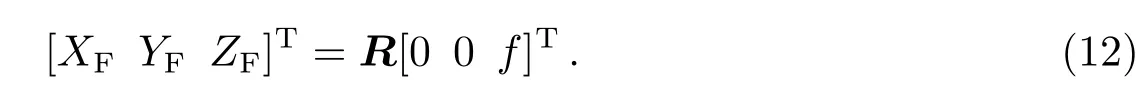
如图5所示,在反射面坐标系统下,由吻合焦点坐标值引入结构指向相对于参考指向在空间位置上的两个中间变量α和β,前者为结构指向同参考指向之间的夹角,后者为结构指向在XOY平面的投影与Y轴负半轴的夹角.结构指向穿过吻合后的焦点F,同时吻合焦点在XOY平面的投影点为PF.

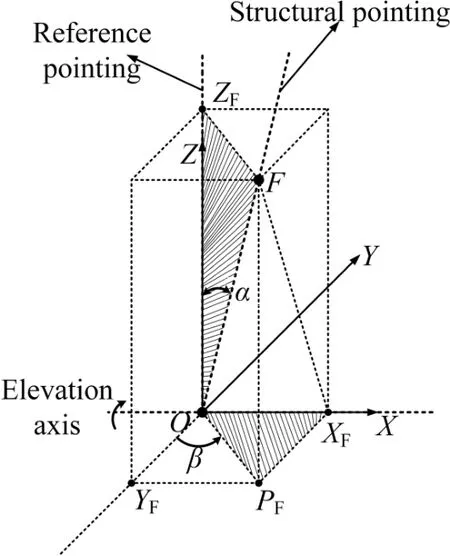
图5 反射面坐标系统下的结构指向Fig.5 Structure pointing of the re flection plane coordinate system

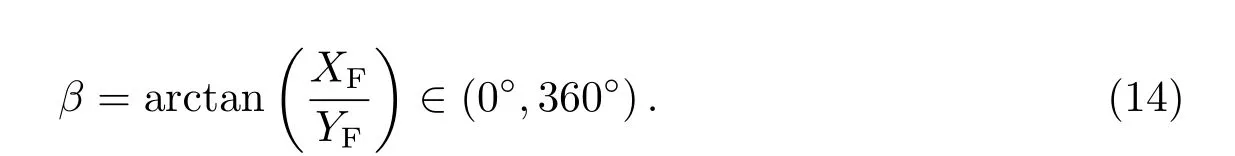
对XOY平面的β角,规定自Y轴负半轴始沿逆时针方向为正方向.为了算法编译的方便,表1对β取值规律进行了归纳.

表1 β角的取值规律Table 1 The value law of β angle

综上,根据(12)式求得反射面坐标系统下吻合焦点的空间坐标值,可获得结构指向的空间方位.进而对由反射体变形引起的指向误差,利用(13)–(14)式对其在反射面坐标系统下的误差空间分布进行表征.

3 指向误差修正

将反射面坐标系统下指向误差的空间分布分解为结构指向相对于参考指向在天线俯仰和方位上的偏差量,并分别命名为∆Elevation和∆Azimuth.

3.1 俯仰角偏差量

前文图5所示,无论射电天线处于何种俯仰工况下,∆Elevation均为结构指向所对应的俯仰平面和参考指向所在俯仰平面的夹角,而与俯仰角Elv无关.故有:

3.2 方位角偏差量

图6所示为不同俯仰工况下天线结构指向示意图,其中g表示重力加速度竖直向下,同时将不易解算的方位角相对偏差量∆Azimuth表征在水平面上.指天时,β即为天线的结构指向相对于参考指向在方位角上的偏差量.并且可以预见,当处于其它不同俯仰工况时∆Azimuth是仅关于α、β和Elv三者的函数.结合图5,由空间几何关系严格推导可得:

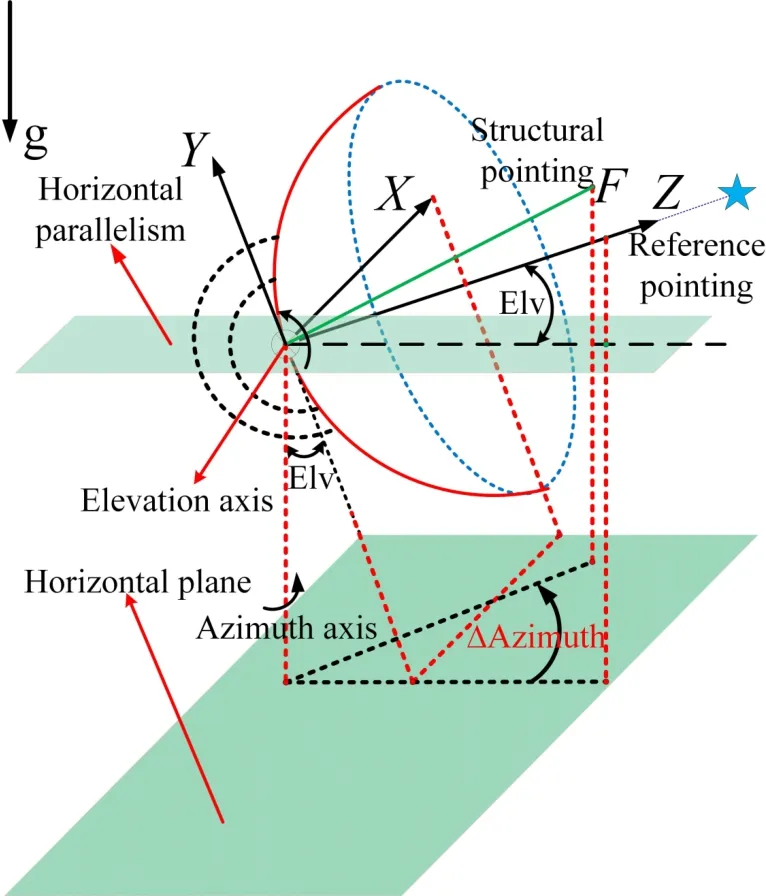
图6 不同俯仰工况下的结构指向Fig.6 Antenna structure pointing under di ff erent pitch conditions

对于水平面中的∆Azimuth,规定沿逆时针方向为正方向.同时为了编程的方便,表2罗列了方位角偏差量的赋值约束条件.

在天线的实际伺服控制中,∆Azimuth绝大部分取值分布在0◦附近极小的一个区间内,仅当俯仰角无限趋近90◦时,∆Azimuth≈β.

表2 方位角偏差量的赋值规律Table 2 Assignment law of azimuth deviation

3.3 指向修正数学模型

由(15)式直接得到俯仰角偏差量,将(13)–(14)式以及俯仰角Elv代入(16)式容易得方位角偏差量.区别于偏差量,为了便于说明修正量,依照图6所示天线实际伺服中俯仰轴、方位轴转动的正方向(均为逆时针),则俯仰修正量取值为−∆Elevation,方位修正量取值−∆Azimuth,可得指向修正数学模型:

其中,Elevation0和Azimuth0为原始目标星源俯仰、方位命令,Elevation和Azimuth为修正后的俯仰、方位命令.

针对应用广泛的卡氏赋形双反射面天线的副面在不同俯仰工况下存在作用于指向偏移的空间位姿误差这一问题,可以利用2018年项斌斌等人建立的天线远场电性能同副面空间位姿调整量的数学关系式[15],直接从副面的空间位置姿态误差导致的天线口径面光程差出发,利用天线的接收机和终端获取电性能数据,进而严格推导出副面的空间位姿调整量.

4 仿真分析

以用于射电天文观测的26 m射电望远镜为分析对象,它的副面直径2.6 m、主面直径为26 m、主面焦距为7.5 m、主反射体几何参数示意图如图7所示.该天线常用工作频段为c波段,频率5 GHz,对应波长0.06 m.天线的最佳预调俯仰角是40◦.

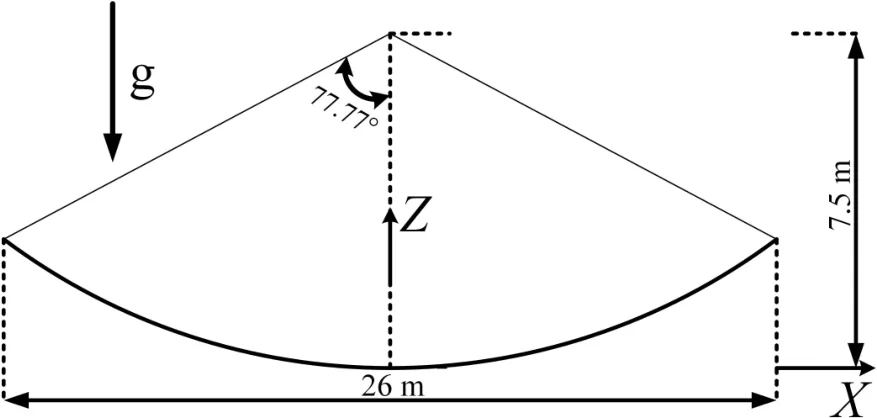
图7 主反射体几何参数示意图Fig.7 Main re flector geometric parameter diagram

4.1 型面定顶吻合量

利用天线的主反射体有限元模型仿真数据进行分析,其中包含8组反射面坐标系统下的主面形变点空间坐标值,分别对应0◦、10◦、20◦、35◦、45◦、60◦、70◦、80◦等不同的天线俯仰工况.联立(7)–(11)式做型面定顶吻合计算后得到旋转量γ和φ(单位mdeg表示10−3度),焦距值f如下表3所示,同时给出了不同俯仰角下各吻合量所对应的拟合误差值.

基于(12)–(16)式的数学算法进行分析可以得出表3中涉及指向误差修正的型面定顶吻合参数仅有γ和φ,而与f无关.随着俯仰角的增大,环境载荷中的重力占主导作用,使得吻合焦距值f随着天线口径的增大而增大,但相对理想焦距值7500 mm的变化始终十分微小.同时结合两个型面旋转量吻合值γ和φ的数据特点观察来看,基于本文提出的型面定顶吻合算法并做严格空间几何推导所建立的指向误差修正模型,会对天线主反射体在高低俯仰上的结构重力变形引起的指向偏差有明显贡献,但对于其它环境因素诸如风、热效应等随机或半随机变量导致的指向误差是较难确定的.然而,如果能对随机载荷进行准确测量,则可以通过结构分析获得结构变形,进而通过本文提出的方法获得相应的指向误差影响和修正量.

表3 天线各俯仰角下型面吻合参数Table 3 Antenna pro file matching parameters under di ff erent elevations

4.2 形变主面的半光程差

将解得的s代入(7)–(9)式,得到图8所示不同俯仰工况下型面吻合前后天线的参考指向和结构指向所对应的半光程差的均方根值(Root Mean Square,RMS).响应前者的均方根值大多集中在1–2 mm之间,而响应后者的均方根值一般分布在0.5–0.7 mm之间.由此说明,3自由度吻合得到的预测结构指向更加接近真实的天线指向,同时佐证了基于吻合量数据推导建立的指向修正数学模型的合理性和精准性.

4.3 天线的指向误差与修正

在数学软件Matlab中对本文提出的3自由度型面定顶吻合算法和指向误差修正算法进行实现,得到用于天线指向校准的∆Elevation和∆Azimuth.为了更好地检验本文的指向误差修正方法,故而利用常见的波束位置偏差[16]去表征天线指向误差的空间分布.波束位置偏差通常由俯仰偏差、横切俯仰偏差两种分量构成.前者同∆Elevation在数值、空间几何意义上完全一致,均与俯仰角Elv无关.对于受到天线俯仰工况角约束的方位偏差量需引入一个乘积系数变量cosElv,则横切俯仰偏差量∆XElevation可表示为:

图8 半光程差的均方根值Fig.8 Root mean square value of half optical path di ff erence

如图9所示不同俯仰工况下的天线波束位置偏差量分布变化图,俯仰偏差的变化区间为−6.5 mdeg到0 mdeg,横切俯仰偏差则分布于−6 mdeg到7 mdeg之间.由图9左图可知,∆Elevation的绝对值随俯仰角的增大而减小,这一规律符合实际环境中当射电天线处于小俯仰角工况时,环境载荷作用下主反射面变形引起的重力方向指向偏差更大这一规律;由图9右图可知,∆XElevation的值分布在零点上下.从其变化规律分析来看,无论是自天线的高俯仰角或是低俯仰角出发,∆XElevation的绝对值均呈现出先变小再变大的变化趋势,同时它的极小值点大约分布于40◦附近,这也契合了26 m射电天线的最佳预调俯仰角是40◦.

基于(17)式得到图10所示不同俯仰工况下的天线指向修正量.从俯仰、方位修正量各自的数值特点分析来看:左图中俯仰修正量值均位于零点上方,符合实际环境中天线指向沿重力方向下垂这一特征;右图中方位修正量的绝对值随天线俯仰角的增大而增大,特别是当靠近仰天位置时会呈几何指数增大,同时其对指向修正的影响作用也愈来愈小.

基于本文所建立的指向修正数学模型分别得到俯仰、方位修正量之后,即可在天线的伺服控制中对俯仰、方位指向误差进行修正,进而提高射电天线的指向精度.

5 总结与展望

本文基于反射面坐标系统下的天线变形主面,提出了一种3自由度最小二乘吻合的型面定顶吻合算法,并且利用空间几何关系严格推导出了射电天线主面变形的指向误差修正量表达式,这对大型射电天线在对主面变形引起的指向精度损失做有效评估及指向精度的提升均具有一定的指导意义.

图9 天线波束位置偏差量Fig.9 Antenna beam position deviation

图10 天线指向修正量Fig.10 Antenna pointing correction

本文主要从几何角度研究了主面变形对天线指向的影响,未考虑在馈源照射情况下结构变形对电磁性能的影响,即认为馈源对主反射面进行了均匀照射.然而,实际天线工作时,多采用近似高斯型锥度函数的馈源照射,反射面不同区域的结构变形对光程的贡献不尽相同.因此,在下一步的研究工作中,我们将考虑天线口径场分布函数的影响,针对天线主反射体内外圈的光程贡献差异构造权重因子,综合考虑结构变形对指向的影响.