“笨”方法也是“好”方法——《鸡兔同笼》单元重组引发的思考

徐晓良

“鸡兔同笼”问题在我国古代数学名著《孙子算经》中就已经出现，为了体现其数学文化历史与独特的解决问题方法，不同版本的小学数学课本都把它纳入其中。“鸡兔同笼”是教学难点，特别是一线教师存在非常多的困惑与问题。一是解题方法上：虽然“鸡兔同笼”问题的解题方法很多，但这些方法都不是平时数学解决问题的常用方法。当学生面对问题时，很难用以前的经验来解决问题；“假设法”是解决“鸡兔同笼”问题非常好的数学方法，但对四年级的学生来讲，“假设法”比较陌生，而且解题步骤较多，要理解解题的每一步表示的意思不容易。二是教学目标上：从教材呈现的解题方法而言，有画图法、列举法、假设法、方程法等。不同版本教材无论把“鸡兔同笼”问题编排在哪个年级，都呈现了多样的方法。学生要把这些方法都掌握起来，难度很大。面对四年级的学生，“鸡兔同笼”问题的落脚点和切入点又在哪里呢？

如何基于学生的认知基础与经验方法，突破教材原有的编排顺序，重构这一典型问题的学习序列呢？笔者在分析研究教材的基础上，对“鸡兔同笼”问题进行了新的探索与实践。从学生学习的起点与导入进行了思考、分析、实践。

一、知事——《鸡兔同笼》问题的多版本教材分析

笔者查阅了九个版本的数学教材，发现《鸡兔同笼》问题在不同版本的教材中均有编排，但编排的年级、解决方法介绍及侧重点是不同的。（见表1）

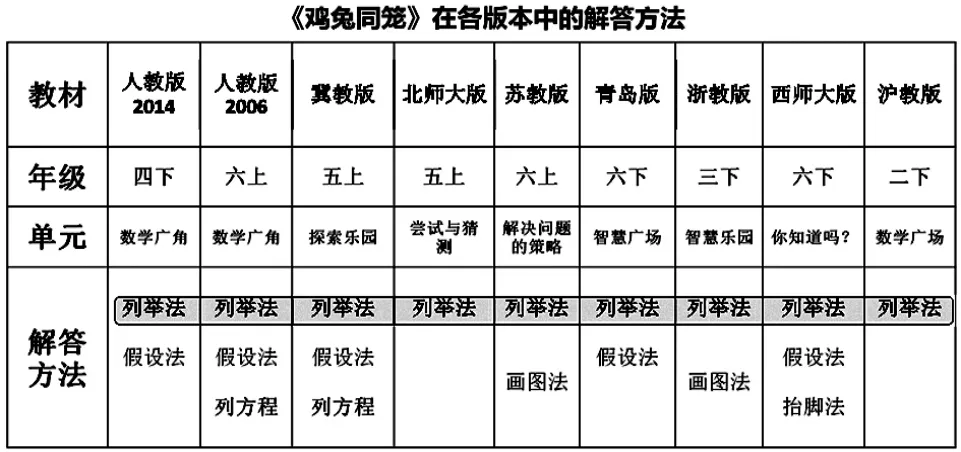
表1

横向比较，不同版本的教材都把“鸡兔同笼”问题作为学习的主题，但不同的教材处理方式与目标定位并不完全一致。有的教材原汁原味地呈现历史原题，体现了数学的优秀文化；有的教材则对原问题进行情节性的改编，突出数学模型思想；也有的以此问题为载体，侧重于“列表枚举”等数学方法的介绍。

纵向比较，人教版将《鸡兔同笼》的教学编排从第十一册（2006年版）前移到第八册（2014年版），且内容编排整体变化不大，教学目标定位略有微调，主要减少了“方程”这种解题思路，其他（含练习题）则大体相同。

综合上述教材的分析，整理成表1，可以看出不同版本的教材在呈现方式与目标定位上的差异，给教学带来了很大的创新空间，与此同时，也带来不少困惑的问题：一是从教学设计的角度，在不同的学习阶段，如何设计“列举法”“画图法”“假设法”“列方程”等方法的学习序列，揭示这些方法内在的本质的联系？二是从数学方法的角度，如何夯实最基本的数学方法，为后继学习积累更有价值的思维经验？

二、知人——《鸡兔同笼》问题的学生学习起点分析

以浙江省海宁市紫微小学（城镇小学）四年级为例，对两个班共88 位学生进行了一次前测：前测内容两题，共计10 分钟时间。

第一题：笼子里有若干只鸡和兔。从上面数有8个头，从下面数共有26 只脚。鸡和兔各有几只？学生的正确率见表2：

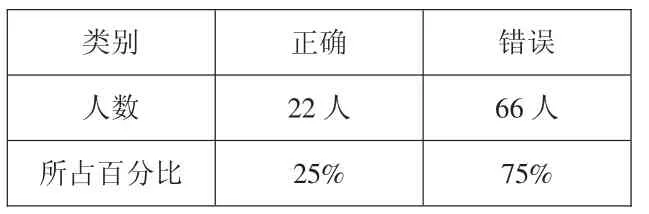
表2

第二题：全班一共有38 人，共租8 只船，大船可以坐6 人，小船可以坐4 人，每条船都坐满了。大小船各有几只？学生的正确率见表3：

表3

从统计结果可见，这两个班的学生无论是“鸡兔同笼”的原题还是变式题，都有四分之一左右的学生能找到正确答案。不同的学校或班级解决此类问题的差异较大，笔者曾在2018年对四年级城镇学校和农村学校各一个班做了同样的前测，城镇学校的正确率远高于农村小学。笔者分析，课前的学习，特别是是否参加课外辅导班的学习，是造成差异的主要因素。

据调查，城镇学校近一半的学生在课外班学过“鸡兔同笼”问题，而农村小学的学生学过的比例很小。即使在城镇学校上过课外班的学生中，能正确解答的学生也只占少数，这说明，对于四年级学生而言，掌握“鸡兔同笼”问题解法有一定的难度。基于问题本身的难度以及学生的差异表现，笔者认为“鸡兔同笼”问题的教学，应当低起点、低难度！

然后，再来看看做对的学生都是采用什么方法做的呢？第一题做对学生采用的方法如表4。

表4

第二题做对学生采用的方法如下表5。

表5

在解决第一题时，做对的学生中有一半是采用假设法的，而到变式题的时候却减少了一半，为什么会这样呢？在整理学生作品的过程中，笔者找到了答案。笔者欣喜地发现有半数以上的学生开始用列举法了，不仅是做对的学生，做错的学生中也有很多开始去列一列、试一试，即使没有找到正确答案。学生的解题过程，印证了笔者的一个想法：许多学生的心中是有列举尝试的意识的，但是，等教师将“鸡兔同笼”的内容教完后，即使没学会假设法的学生，也不愿意用列举这种“笨”办法了。

三、润慧——“鸡兔同笼”单元重组学习路径

知识是载体，通过数学知识的学习培养学生的数学能力，特别是思维能力与解决问题的能力才是教学的根本目标。而能力体现在知识的迁移与运用上，面对一个不曾遇见或是略有挑战的数学问题，学生能运用已学的知识和思维经验去解决它，这是能力的体现。比能力更高级的是智慧，智慧体现在选择中。“鸡兔同笼”问题解决的方法比较多样，如何选择合适的方法？如何避免对方法的生搬硬套？

通过对多版本教材的对比分析，结合对学生的问卷调查，笔者认为：“鸡兔同笼”单元的学习必须要“保底”与“提升”。保底，即人人掌握用列举法解决“鸡兔同笼”问题。提升，即通过多种方法比较分析，找到方法之间的联系，深度理解“假设法”，从而实现不同的学生都有不同的层次提升。让没有接触过的、能力较弱的学生在束手无策时，有法可循；让有一定学习基础、一知半解的学生想套用模型时，真正理解；让已经掌握了的、能力较强的学生在正确解答时，深度理解。见表6 具体安排。

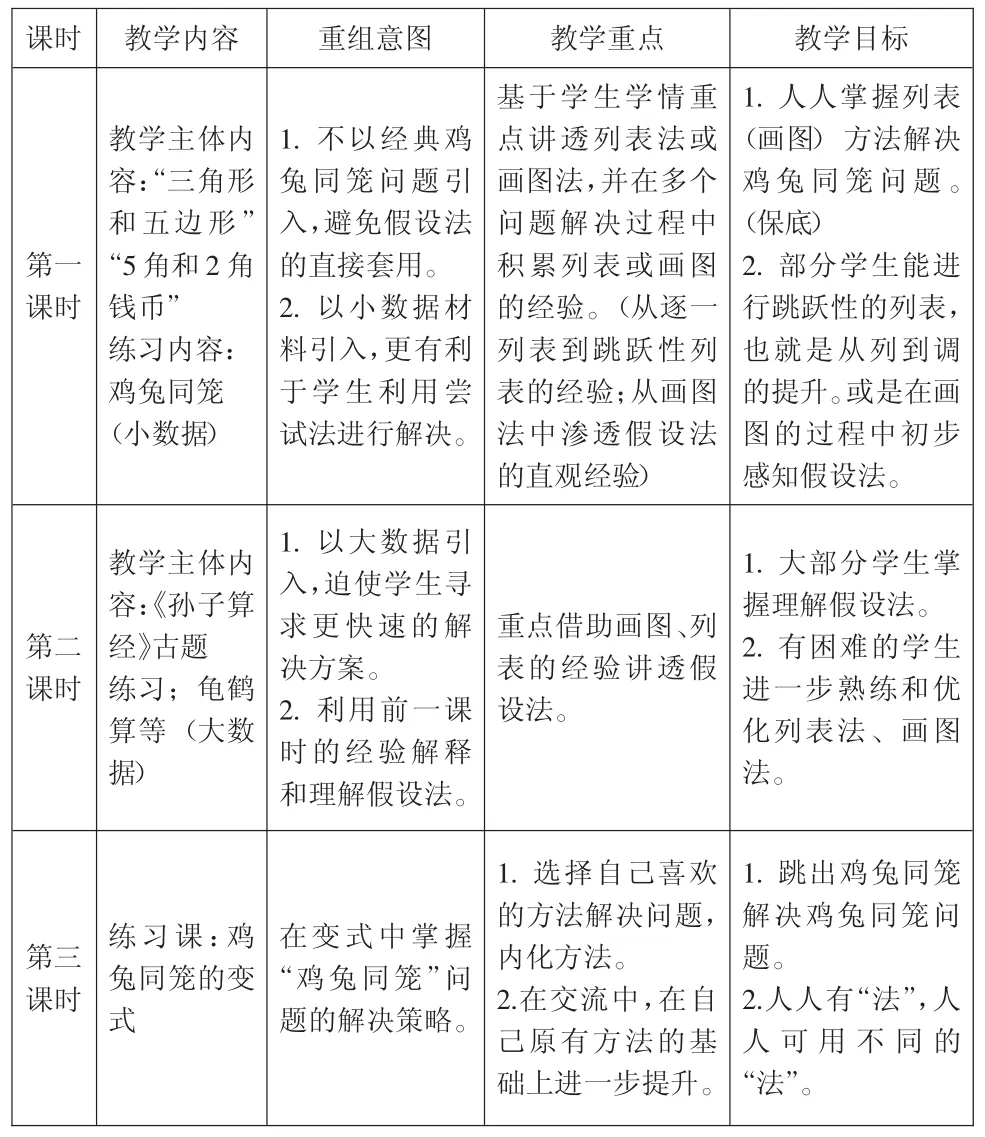
表6

1.回归学生起点，人人掌握“列举法”。

从解题方法的角度而言，方程法远比画图、列表之类的方法要快捷、简便，但这种简便是数学的价值而不是教育的价值！对于数学广角的内容和学生学习的价值不仅仅只是停留于得到一个答案和结果，更多的是要给予学生解决面对新的、未知问题时的一种方法和策略，如：面对新问题如何入手？从哪里入手？怎么进行尝试？怎么样在尝试的过程中发现和总结？通过对教材内容的重组，在课堂上呈现非典型“鸡兔同笼”问题，让学生回归到学习最原始的状态，从未知开始，尝试画一画、举一举的方法解决问题，在解决问题的过程中慢慢积累经验，在经验中一步一步地优化、提升。放慢脚步，拉长并放大列举、画图等基本方法的学习与体验过程，拉长了列举法的体验，学生原生态的思考、探索、分享、实践有了时间与空间的保障，有序思考，观察、分析、归纳、创新、发现并不断调整等综合能力都得到充分发展。这样的学习过程，既守住了学生学习的底线，更让许多数学核心素养在学习过程中得到了培养。

2.拉长体验过程，深度理解“假设法”。

面对两极分化相对比较严重的“鸡兔同笼”问题，重组后的第一课时貌似忽略了“优秀学生”的存在。但回归原始，并不是放弃假设法，而是拉长体验的过程，给假设法做了更深更厚的铺垫。在课堂上难免有优秀分子会提出假设法，而太快得出如此“简易而通吃”的方法，往往会忽视了结果背后的产生过程。假设全是鸡或兔，逼近的思想在画图法、列表法中都是有渗透的，拉长了这个过程，给予“没有接触过或能力弱的孩子”一个理解的机会，给予“貌似理解假设法的孩子”一个走进假设法背后的机会。而且，第一课中的两个例题都不是典型的“鸡兔同笼”问题，而是用三角形与五边形，5 角与2 角这样的素材，进一步避免了部分学生套用公式，也从本质上来理解这些数学问题。

3.多次沟通融合，联结提升各方法。

本单元的重组中，实现了两次沟通融合。第一次融合是在第一课时例1 的学习中，要求学生完整列举并将所有情况有序写出来。例2 的学习则引导学生思考：当找到正确答案时，还需要列举下去吗？通过对这一问题的讨论，最后学生发现：当找到正确答案时，不需要再列举下去了，再往下列举要么是多相差数，要么少相差数。例3 问题呈现时，要求学生快速列举。这时，学生已能利用先前学习获得的经验，开始跳跃式的列举，从随意举2 个数后根据相差数快速地调整到正确的答案，而快速调整的过程其实就是假设法的雏形。第二次融合是在第二课时，在学习了假设法后，再回头引导学生比较列举法与假设法，学生突然发现列举法就是假设法，假设法只不过是从特殊的数字开始，而列举法则是从普通的情况开始，其本质不变的是关注假设总数与原总数的相差数与两种不同物体的相差数。这两个层面的沟通融合，让学生产生顿悟，让学生豁然开朗。

单元重组的目的是构建更加适合学生的学习序列，科学设计学习序列，可以降低学生学习的难度。与此同时，在不同的学习阶段，学生学习的解决问题的方法是不一样的，积累的思维经验也在动态变化。每一种方法都有适切的应用场景吗？什么是好的方法？从数学的角度看，简洁通用的方法就是好的方法，从教学的角度看，适切的方法就是好的方法，特别地，有时学习的“笨”方法会被新的方法替代，但不能“忘本”，因为那些基本的方法虽然比较繁琐，却是非常通用且比较容易入手的。“笨”方法其实也是“好”方法。