坚持混而不错 寻求最佳平衡——兼评张森、居晓红老师《平行与垂直》一课

刘松

苏步青先生有一句名言“中小学教材可以混而不错”。“不错”是大前提，关注的是大方向、本质，“混”是放松严格性的要求，现阶段讲不清楚的问题用写意的方式说明，但仍不失其真。张奠宙教授也认为，随着教育的普及，数学课程成为人人必修的科目，“简单化”的大众数学也就随之而来，这就要求我们在教材编写和教学实践中采取适当的非形式化方法深入浅出地处理某些数学内容，让学生容易接受，例如长度、面积、体积的概念，只能模糊地描述，总不能要求中小学生去理解“某集合类上定义的有限可加、运动不变的正则测度”。所以说，大众数学是“混而不错”的实践背景。

从张奠宙先生的话语中，我们可以清晰地感觉到，“混而不错”的原则不仅适用于教材的编写，同样适用于日常的教育教学。对此，笔者特别认同，但笔者关心的是，我们的日常教学中，在坚持“混而不错”原则的同时，如何把握“混”的度？换句话说，能否尽力在“严格”和“通俗”（或者说“理性”与“经验”）之间求得最佳平衡？

自从转任专职教研员后，听课几乎成了工作的全部。经常听到许多教师在课堂上随口说出一些看似通俗、严谨，其实逻辑有误的结论。比如，在讲到角的大小和什么有关、什么无关时，教师们习惯的说法是：角的大小和边的张开度有关，和边的长短无关。笔者自己之前也这样说，也曾听许多特级教师、正高级教师这样说过。这话似乎没什么问题，但随着自我学习的提升，突然有一天，意识到了这句话内在的逻辑矛盾。在中小学阶段，角的两种定义，无论是静态的（从一点引出的两条射线所组成的图形叫做角），还是动态的（一条射线绕着它的端点旋转, 旋转起始位置与旋转终止位置所组成的图形叫做角），角的两条边都是射线，而射线无限长，怎么会有长和短？一旦有了长和短，就成了线段，可角的两条边明明是射线，岂不矛盾？当与教师们交流如上想法时，许多教师似有所悟，转而追问，这话自己说了许多年，也没觉得有问题，应该怎么改才能既不失数学的本真，又让小学生感觉通俗易懂呢？

至于怎么改？笔者相信最高级的智慧在民间，广大教师一定都有自己的想法。笔者目前给自己区内的教师是这样答复的：角的大小和两边的叉开度有关，和两边画出来的长短无关。不知可否？恳请各位专家老师批评指正。

之所以提到上述案例，是想表达，在小学数学课堂里，似乎这样的例子还有许多。比如，《平行与垂直》一课的教学。

《平行与垂直》作为小学数学图形与几何领域的一节典型课例，许多教师都曾有过精彩的设计。梳理一下，大致方法是，先要求学生在纸上画一条直线，再画另一条直线。提出问题：想一想，你后来画的这条直线和先前画的直线有怎样的位置关系？可以分为几种情况？或者直接让学生在作业纸上任意画两条直线，而后呈现不同的作品，再让学生根据不同的位置关系分类，最后一步步分析归纳出平行和垂直的概念。如此教学，尊重学生学习的前概念，纯数学导入，问题驱动，层层递进，可谓经典。上述教法，无论是小问题层层递进，还是大问题直接抛出，在后续解释平行概念时，都会遇到如下情况：（a、b两条直线是否平行？）

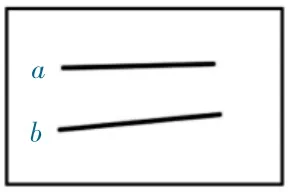
图1

为了让学生明白图1 中a、b两条直线不平行，是相交的，几乎所有的教师都会说“请把两条线延长，看看会怎样？”学生也一定会在教师的引导下画出延长线，感悟到相交现象。但问题是，教师一张嘴，就默认了a、b 两条线不是直线，是线段。因为直线本身是无限长的，无需延长，只有线段才能或者才需要延长。这里遇到的问题和上述角的例子一样，都是在有限空间里如何讲明无限的问题。当然，说到这，也许会有教师说，直线无限长无法画出，这里的a、b 就是线段，只能借用平行线段来讨论研究平行线，对此，笔者完全认同。回到一开始的问题，此刻，我们教师在坚持混而不错的同时，能否有更精准的表述？笔者常常想，学生之前学过直线的概念，也知道直线是无限长的，在这种情况下，教师是否可以这样说：目前看着没相交，别忘了直线都是无限长的，现在纸张足够大，请把a、b 两条直线的“真身”显影出来（或者说，请把a、b 两条直线画完整些），再判断是否相交。当然，也许会有教师说，什么叫把直线画完整些？把直线画完整些还不就是延长吗？对此，笔者也完全认同。这肯定不是最佳的表达，只是笔者目前想到的表述而已。笔者想表达的意思是，如此表述，是否既坚持了“混”，又越来越接近“不错”了呢？也恳请各位专家老师批评指正。

说到借助平行线段解释平行线，笔者马上又想到了另一种情况。（如下两幅图）

图2

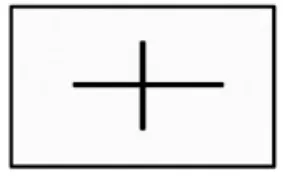
图3

此刻，若判断图3 中相交的两条直线是否垂直，学生只需用三角板上的直角或者量角器去量一下，学生看得见、摸得着。但若判断图2 中两条直线是否为平行关系，学生怎么办？难道只凭感觉两条直线不相交？当然不可以，我们教师也有的是办法。常用的办法之一就是让学生把线延长、延长再延长，看看真的没相交，所以是平行。显然，这不是上乘之法，在有限的时空里，永不相交感受不深。但若借用信息技术，让学生在电脑上直观动态地感知，上述两条直线向左右两个方向不断地延伸，但一直不会相交，倒不失为一种很好的弥补办法。所以，前文张森老师的教学设计，充分利用信息技术的加持，值得点赞！还有一种比较好的做法，许多教师会把两条直线放在格点图上，如前文居晓红老师一样，如图4。学生会更直观地感悟到，格点间距离不变，当然两条直线不会相交。相比而言，后一种方法兼顾了“方向相同”和“距离相等”两种直觉，更容易看得见和摸得着。如此教学，逐步接近了波利亚的教导：抽象的道理是重要的，但要想尽一切办法让学生看得见、摸得着。

图4

之所以让小学教师们要绞尽脑汁地想出办法使学生明白平行线的判定，原因不仅仅是小学里没学平行线的判定定理及性质定理，根本原因出在中小学教材里平行线的定义上。以人教版教材为例，中小学基本一致，都是同一平面内不相交的两条直线称为平行线。《几何原本》定义23 提到，“平行线是在同一平面的直线，向两个方向无限延长，在不论哪个方向它们都不相交”，这就是说，小学、中学、《几何原本》里的平行线定义都差不多，但都不能用于检验。所以，有专家说，某种意义上，平行线的概念似乎并不重要，重要的是如何判断平面上两条直线是否平行。怎么判断呢？两条直线无限延长后是否相交，是无法检验的，必须借助第三条直线，用同位角相等来检验，但这又是中学的内容了。因此，小学里如何依据直观判定两条直线平行是一个难题。平行线的概念不能检验，当然无法作为判定定理。据说，当年的古希腊数学家也为此大伤脑筋。他们原以为从平行线的定义和其他公理可以推出“平行线被另一条直线所截的两个同位角相等”这样的结论来，可是反复思考都没有结果。正因为如此，欧几里得才在《几何原本》里加了一条公理［欧几里得第五公设（改进版）］：同平面内一条直线与另外两条直线相交，如果一侧的两个内角和为平角，那么这两条直线平行。另外一个改进版是：过直线外一点，有且只有一条直线与该直线平行。还有一个等价的命题是：同位角相等，两直线平行。显然，这些中学才能学到的第五公设相关内容无法给小学生讲明白，但是否可以有机渗透呢？答案是肯定的。

再者，站在学生的立场，基于儿童的视角，针对平行和垂直两个相对抽象的概念，哪一个更容易掌握呢？估计多数会选垂直，因为直观可检验。但人教版等版本教材均是先学平行（不相交），而后学习相交及特例（垂直）。如此安排，有其内在逻辑性，但这种编排并非教材编写的绝对，自然也不应是课堂教学的唯一。有些版本教材则采用了另外一种编排顺序，先学垂直，而后平行。相比而言，笔者更喜欢后一种编排。行文至此，应该给前文的居晓红老师点个赞，她的教学设计就是先垂直而后平行的，看得出来，居老师非常尊重教材，教学完垂直后，直接引出了平行的概念。对此，略感遗憾！既然垂直的概念学生已明白，那么为什么不可以让它为平行概念的建立贡献点力量呢？笔者想到了张奠宙教授曾经的建议：田径场上，110 米跨栏比赛的各条跑道线都和起跑线垂直，它们具有相同的方向，所以不管怎样无限延长，跑道线都不会相交，所以它们是互相平行的。如此，背后用到了垂直于同一直线的两条直线互相平行的判定定理，等价地用到了同位角相等，两直线平行的判定定理。而显性的好处是，有了垂直做基础，等于给学生感悟方向相同搭建了一个绝好的支架。

“方向相同”的直觉，从知识层面上分析，与中学里“同位角相等”概念的衔接比较顺畅，所以，许多教师都在用，进而总结如下结论：两条直线只要方向一致，就不相交，故而平行。对此，笔者完全赞同，但若再进一步，笔者想说，可否把“方向一致”改为“方向完全一致”，继而，教材中平行线的定义，可否回归《几何原本》的表述，强调两个方向，永远不相交。如此，虽然丢失了定义的简洁性，但对促进学生理解概念而言，是否可以增强其深刻性呢？当然，也许会有教师说，方向一致的意思中就有完全一致的内涵，歪斜一点点都不能叫一致。对此，笔者也完全认同。但对学生而言，面对类似上面图1 的情况，是否有人认为，两条线都是东西走向（按地图方位），方向也可以说一致呢？当然，更准确的说法应是基本一致。至此，笔者想到了有些地方教师晋职称需要论文鉴定，鉴定级别就分了不符合、基本符合、符合和完全符合四个层次，显然，这里的符合和完全符合就有程度上的差异。学生在生活中也多多少少会有类似赞同和完全赞同略有差异的相关经验（比如选班干部时），若果真如此，基于学生的生活经验，从更有利于学生准确把握概念实质的角度，多说一两个字，是否更有效呢？事实上，从前文两篇教学实录中可以看到，教师们已经注意到了对教材中相对简洁的概念定义的语义丰富，但对方向一致的问题，似乎强调与解释得不够。

以上仅是笔者在学习“混而不错”时的一些随想和感悟，如若深究下去，可能要涉及先界定相关词语内涵的问题，限于篇幅，不再赘述。有些许抱歉，张森和居晓红两位教师的教学中还有许多优点未曾提及，当然也有一些不足未做深入分析。但希望上述观点对两位教师能有所启发，也希望有更多的教师在教学中能求得“严格”与“通俗”间的最佳平衡。