双圆弧齿廓谐波齿轮传动优化设计方法*

2020-12-01沈云波支立辉贾婧瑜朱育权

西安工业大学学报 2020年5期

沈云波，支立辉，贾婧瑜，朱育权

(西安工业大学机电工程学院，西安 710021)

谐波齿轮传动由波发生器、柔轮和刚轮构成，通过柔轮的弹性变形实现柔轮和刚轮啮合的一种行星齿轮传动形式[1]，具有高速、高效、大承载力和结构紧凑等优点，广泛应用于军事领域、航空领域和机器人研究领域等需要高端机械装备传动装置的特殊领域[2-3]。文献[4]采用直线作为谐波齿轮齿廓，保证了定传动比和一定的承载能力，但设计中没有考虑到柔轮轮齿传动中的法向变形，因而不能得到很好的传动性能。由于渐开线齿廓研制较为简单，从20世纪60年代起，渐开线齿形是目前发展最为成熟且应用最广泛的一种齿廓曲线[5]。但渐开线谐波齿轮在空载状态下，共轭区域小，柔轮受载变形后易产生边缘接触，甚至尖点接触等问题。不同于渐开线齿形，双圆弧齿形谐波齿轮传动啮合中的双共轭使该传动系统具有更大的承载能力、更高的传动精度和较小的启动力矩[6]。因此，研究双圆弧齿廓谐波齿轮传动具有一定的学术意义和较高的应用价值。波发生器使得柔轮产生弹形变形并与刚轮啮合传动，因而柔轮变形啮合转角的计算就比较复杂。文献[7]提出了一种计算方法，简化了柔轮变形转角的计算过程，但仅适用于对传动精度要求不高的情况；文献[8]给出了高精度谐波齿轮设计中柔轮变形转角的精确计算方法，但总体计算量较大，且计算过程易出错；文献[9]总结了两种谐波齿轮啮合方程的建立方法，一是通过曲线包络法建立啮合方程；二是利用运动学法建立谐波齿轮的啮合方程，并详细论证了这两种方法的可行性。此外，在谐波齿轮传动啮合仿真分析、新材料应用和刀具设计等方面，国内外学者均做了大量研究工作，其研究成果对后续研究的开展具有重要参考价值[10-15]。因此，在上述研究的基础上，考虑柔轮变形后中线伸长，提出柔轮在啮合中转角位置计算的方法，根据谐波齿轮啮合理论，建立由柔轮齿形推导刚轮齿形的模型，以齿侧间隙最小、有效啮合齿高最大为优化目标，采用加权求和法建立多目标优化数学模型，进行谐波齿轮齿廓参数优化和仿真分析。

1 谐波齿轮传动数学模型

谐波齿轮运转中柔轮中线的变形规律由波发生器决定，其直接影响谐波齿轮的传动性能。因此，根据已知的数学模型和柔轮中线变形规律研究刚轮和柔轮轮齿间的啮合关系，即是研究如何确定刚轮的齿廓数学模型。

1.1 柔轮双圆弧-直线齿廓数学模型

图1 柔轮双圆弧-直线齿廓Fig.1 Double arc flexspline-straight tooth profile

(1)

式中：xM为点M在X1方向的坐标；yM为点M在Y1方向的坐标；r为分度圆半径。

(2)

(3)

式中：xN为N点在X1方向的坐标；yN为N点在Y1方向的坐标；z1为齿数;ad为齿顶宽度。

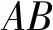
(4)

右侧BC段切线齿廓数学模型：

(5)

式中：rBC为BC段上点的坐标；nBC为BC段上点的公法矢；满足s∈(l1,l2)，l2=l1+h1/cosδ，其中h1为直线段径向高度。

(6)

1.2 柔轮转角精确计算方法

图2 谐波传动坐标系Fig.2 Coordinate system of harmonic drive

考虑柔轮中线在变形后有少量伸长，计算1/4圆周上的伸长量，并将其平均分配到1/4圆周上的每个轮齿中，则有

(7)

其中lw为每个轮齿所对应的中线伸长量。

设1/4圆周上第i个齿对应的共轭角度为φ1，顺时针旋转的角度为正，则图2中各角度关系为

(8)

其中u0为柔轮轮齿的最大径向变形量。

1.3 刚轮齿廓数学模型的建立

柔轮和刚轮两齿廓共轭接触，由运动学法推导两齿廓共轭传动的啮合方程如下：

(9)

式中：ni为齿廓上接触点的公法矢；ri为柔轮齿廓坐标；B为关系矩阵，且

(10)

实际上式(9)中只含一个未知量φ1，也称为谐波齿轮传动的共轭角度，φ1值确定的区间为柔轮和刚轮的共轭区域。

由图2所示坐标系，柔轮坐标系S1到固定坐标系S2的坐标变换矩阵为

(11)

则刚轮理论齿廓的数学模型如下：

(12)

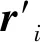
计算得到柔轮齿廓的共轭齿廓。已知一个弧长离散点对应两个φ1解，则一组弧长离散点对应两组φ1解，因此，刚轮的理论齿廓有两条。

2 谐波齿轮齿形优化设计

多齿对啮合是谐波齿轮保持传动稳定性和承载能力的重要条件，其取决因素有两条：一是装配状态下侧隙分布，齿侧间隙减小且啮合区间变化不大时更容易形成多齿对啮合；二是柔轮的有效啮合齿高，轮齿接触面随有效啮合齿高增大而增大，从而改善柔轮的受力状况。因此，齿形优化的目的在于优化齿侧间隙和有效啮合齿高，提高谐波齿轮传动的平稳性。

2.1 目标函数与优化变量

齿侧间隙是相互啮合齿面间沿圆周方向的最小间隙，未受载时的齿廓间最短距离称为法向齿侧间隙，齿侧间隙与最短距离的关系如图3所示。固定坐标系S2(O2，X2，Y2) 与柔轮轮齿固连；A1为变形后柔轮轮齿上某一齿廓点；α1为A1点的法线n斜率；B1为法线与刚轮齿廓的交点；α2为直线A1O2斜率。

图3 齿侧间隙与最短距离的关系Fig.3 The relation diagram between gear backlash and the shortest distance

将柔轮齿廓离散化为k-1段，即过这k个离散点作法线，有k条法线与刚轮齿廓相交，获得沿法线的k个距离(L1，L2，L3，…，Lk)，则

(13)

式中:Lmin为法向间隙；jmin为齿侧间隙。

求解式(13)中的jmin的值，且共轭角度φ1不同，所得出的jmin的值不同。有效啮合齿高为

hn=rag-rab+u0。

(14)

式中：hn为有效啮合齿高；rag为柔轮齿顶圆半径；rab为刚轮齿顶圆半径；u0为柔轮轮齿的最大径向变形量。

最小目标函数为

minF(X)=w1·jmin+w2·hn。

(15)

式中：F(X)为目标函数；w1为齿侧间隙的权重；w2为有效啮合齿高的权重。

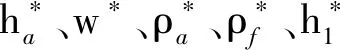
2.2 优化实例

谐波齿轮参数如下：模数m=0.35 mm，柔轮齿数z1=160，刚轮齿数z2=162，顶隙系数c*=0.35，节厚比k=1.3，柔轮凹齿廓圆弧所对应圆心角αf=28°。优化前后的柔轮齿廓参数、刚轮齿廓参数见表1和表2。

表1 优化前后柔轮齿廓参数Tab.1 Flexspline profile before and after optimization

表2 优化前后刚轮齿廓参数(mm)Tab.2 Rigid gear profile before and after optimization(mm)

根据优化的各种变量参数，计算得到优化前后侧隙值分别为3.5 μm和2.4 μm；优化前后有效啮合齿高分别为0.455 mm和0.433 mm。即优化后的齿侧间隙相对于优化前的齿侧间隙减少了1.1 μm，有效啮合齿高减小了0.022 mm，相对于齿侧间隙，有效啮合齿高的变化不大。

3 谐波齿轮传动啮合仿真分析

3.1 共轭区域分析

构建轮齿数学模型，结果如图4所示。以啮合弧长S为横坐标，以共轭角度φ1为纵坐标，得到优化前后的共轭区域比较图；其中有两条曲线分别代表不同的共轭区域，下侧曲线所代表啮合区共轭区域，上侧曲线代表啮入区共轭区域。“双共轭”现象是双圆弧齿廓所独有的，即任意取一个啮合弧长值，分别对应两个共轭角度值，则在未受载情况下，齿廓的同一位置处有两个轮齿在参与啮合；任意取一个共轭角度值，将会在上方曲线或下方曲线处对应两个啮合弧长值，即同样在未受载情况下，柔轮齿廓上同时有两点参与啮合。实线表示优化前共轭区域，虚线表示优化后共轭区域，发现两虚线和两实线轮廓近似相同，优化前后共轭区域无明显变化。

图4 优化前后共轭区域比较Fig.4 Comparison of conjugate regions before and after optimization

3.2 柔轮运动轨迹分析

以一定的角度将柔轮旋转，使其轮齿刚好位于刚轮齿槽内，从而能完整地模拟柔轮轮齿啮合的运动轨迹，明显观察到两个轮齿间的侧隙变化情况，运动的总体轨迹如图5所示。图5可以清晰地看到柔轮轮齿从右下方啮入与刚轮啮合，完全啮合后从左下方啮出，最终脱离，整体运动轨迹是内凹曲线，每一个轮齿的位置所对应一条运动轨迹。同时，柔轮齿廓始终在刚轮齿廓内部，运动过程中没有产生干涉。

图5 柔轮总体运动轨迹Fig.5 The overall trajectory of the flexspline

3.3 齿侧间隙对比分析

由于柔轮轮齿的运动情况均相同，所以，仅需考虑其中任意一个轮齿的啮合过程，仿真得到的侧隙分布如图6所示。从图6可以看出，整个过程中侧隙值始终大于0，即整个啮合过程没有发生干涉现象。在轮齿啮合过程中，侧隙值基本都在6 μm以下，即在这种条件下受载传动的侧隙值得以补偿。同时，运动过程中多齿啮合可以保证较高的承载能力和稳定性。